You are given the following data:
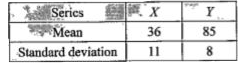
Correlation coefficient between x and y=0.66. Find the equations of the lines of regression.
The correct Answer is:Regression equation of y or x : y = 0.48 x + 67.82
Regression equation of x or y : x = 0.91 y - 41. 35
Step by step video, text & image solution for You are given the following data: Correlation coefficient between x and y=0.66. Find the equations of the lines of regression. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If the regression coefficients be given byx=1.6andbxy=0.4 then find the sum of the slopes of the two regression lines.
View SolutionThe following results were obtained with respect to two variable x and y:
∑x=30,∑y=42,∑xy=199,∑x2=184,∑y2=318,n=6.
Find the following:
(i) The regression coefficients.
(ii) Correlation coefficient between x and y.
(iii) Regression equation of y on x.
(iv) The likely value of y when x = 10.
View Solution
Knowledge Check
If the two regression coefficients are - 0.4 and -1.6, then the coefficient of correlations is
A0B−0.9C0.8D1
From the following data, find () regression coefficients (ii) regression equations.

View SolutionFrom the following data, find (i) regression coefficients (ii) regression equations
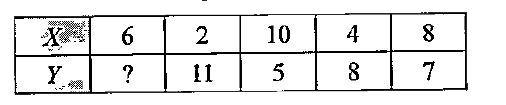
View SolutionFrom the following data, find
Regression equations.
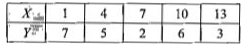
View SolutionFind the regression coefficient byxandbxy when the lines of regression are
6x−5y+10=0,10x−3y−28=0.
View SolutionThere are two series of index numbers: P for price index and S to stock of a commodity. The mean and standard deviation of P are 100 and 8 and of S are 103 and 4 respectively. The correlation coefficient between the two series is 0.4. With these data, obtain the regression lines of P on S and S on P.
View SolutionThe coefficient of correlation between the values denoted by x and y is 0.5. The standard deviation of x is 5 and that of y is 4. Find the angle between the lnes of regression.
View SolutionYou are given the following data, obtain the regression equation and estimate the yield of crops when the rainfall is 29cm. Given that coefficient of correlation between yield and rainfall= 0.52
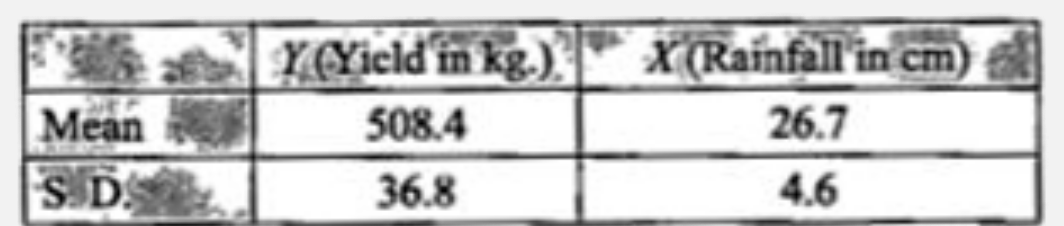
View Solution
