Complete Solutions to अभ्यास प्रश्न 7.3 of chapter त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | त्रिभुज |
| BALAJI PUBLICATION | अभ्यास प्रश्न 7.3 |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
यदि `triangle ABC ~ triangle DEF` तथा AB = 1.2 सेमी तथा DE = 1.4 सेमी है तो `triangle ABC` और `triangle DEF` के क्षेत्रफलो का अनुपात ज्ञात कीजिए |
View Solutionयदि `triangleABC ~ triangle DEF` तथा `triangle ABC` का क्षेत्रफल 9 सेमी`""^(2)` है और `triangle DEF` का क्षेत्रफल 16 सेमी`""^(2)` है व BC = 2.1 सेमी है तो EF ज्ञात कीजिए |
View Solutionयदि `triangle ABC ~ triangle DEF` है, यदि (`triangle ABC)` का क्षेत्रफल = 36 सेमी`""^(2), (triangle DEF)` का क्षेत्रफल = 64 सेमी`""^(2)` तथा DE = 6.2 सेमी है तो AB की लम्बाई ज्ञात कीजिए |
View Solutionयदि `triangle ABC ~ triangle DEF` तथा `(triangle ABC)` का क्षेत्रफल = 16 सेमी`""^(2),(triangle DEF)` का क्षेत्रफल = 25 सेमी`""^(2)` तथा BC = 2.3 सेमी है तो EF ज्ञात कीजिए |
View Solutionदो समरूप त्रिभुजों के क्षेत्रफलो क्रमशः 81 सेमी`""^(2)` तथा 49 सेमी`""^(2)` है | उनकी संगत ऊँचाइयों का अनुपात ज्ञात कीजिए तथा उनकी संगत मध्यिकाओं का अनुपात भी ज्ञात कीजिए |
View Solutionयदि `triangleABC ~ triangle DEF` तथा BC = 3 सेमी, EF = 4 सेमी और `(triangle ABC)` का क्षेत्रफल = 54 सेमी`""^(2)` है तो `triangle DEF` का क्षेत्रफल ज्ञात कीजिए |
View Solutionदो समद्विबाहु त्रिभुजों के शीर्ष कोण समान है तथा उनके क्षेत्रफलो का अनुपात 36:25 है | तब उनकी संगत ऊँचाइयों का अनुपात ज्ञात कीजिए |
View Solution`triangle ABC` में, D तथा E क्रमशः AB तथा AC के मध्य बिंदु है | `triangle ADE` और `triangle ABC` के क्षेत्रफलो का अनुपात ज्ञात कीजिए |
View Solutionदो समरूप त्रिभुजों के क्षेत्रफल क्रमशः 169 सेमी`""^(2)` तथा 121 सेमी`""^(2)` है | यदि बड़े त्रिभुज की बड़ी भुजा 26 सेमी है | तो छोटे त्रिभुज की बड़ी भुजा ज्ञात कीजिए |
View Solutionदिये गये चित्र में, PB तथा QA, रेखाखण्ड AB के लंबवत है | यदि PO = 5 सेमी, QO = 7 सेमी तथा `triangle POB` का क्षेत्रफल = 150 सेमी`""^(2)` है | तो `triangle QOA ` का क्षेत्रफल ज्ञात कीजिए |
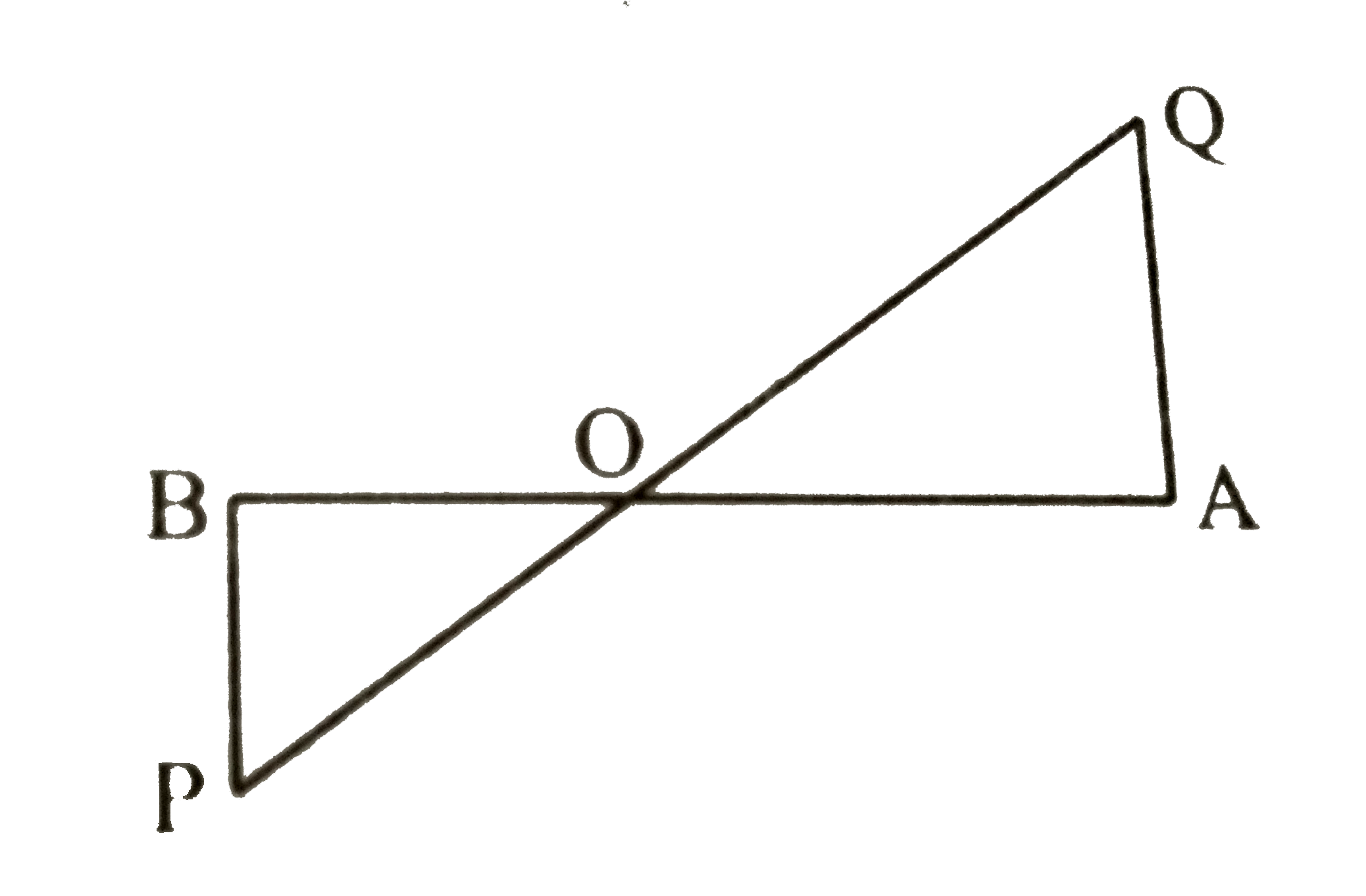
View Solutionदो समरूप त्रिभुजों ABC तथा PQR के क्षेत्रफलो का अनुपात 9 : 16 है यदि BC = 4.5 सेमी है तो QR की लम्बाई ज्ञात कीजिए |
View Solutionदो समरूप त्रिभुजों के क्षेत्रफल क्रमशः 100 सेमी`""^(2)` तथा 49 सेमी`""^(2)` है | यदि बड़े त्रिभुज की ऊंचाई 5 सेमी है तो दूसरे त्रिभुज की संगत ऊंचाई ज्ञात कीजिए |
View Solutionसिद्ध कीजिए कि एक वर्ग ABCD की एक भुजा BC को आधार लेकर बने एक समबाहु त्रिभुज BCE का क्षेत्रफल, विकर्ण AC को आधार लेकर बने समबाहु त्रिभुज के क्षेत्रफल का आधा होता है |
View Solutionएक समकोण त्रिभुज की एक भुजा पर समबाहु त्रिभुज खिंचा गया है | तो सिद्ध कीजिए कि वर्ण पर बने त्रिभुज का क्षेत्रफल, अन्य दो भुजाओं पर बने त्रिभुज के क्षेत्रफलो के योग के बराबर है |
View Solutionएक त्रिभुज ABC है | PQ एक सीधी रेखा है | AB, P में मिल रही है | तथा AC,Q में, यदि A P = 1 सेमी, PB = 3 सेमी, AQ= 1.5 सेमी, QC = 4.5 सेमी है | तो सिद्ध कीजिए कि `triangle APQ` का क्षेत्रफल, `triangle ABC` के क्षेत्रफल का ` (1)/(16)` है |
View Solutionदो समरूप त्रिभुजों की संगत ऊँचाइयाँ क्रमशः 6 सेमी तथा 9 सेमी है | उनके क्षेत्रफलो का अनुपात ज्ञात कीजिए |
View Solution`triangle ABC` में, भुजा AB,P द्वारा विभाजित है | तथा `AP : PB = 1:2`, AC पर एक बिंदु Q है | तथा `PQ ||BC` है | `triangle ABC` के क्षेत्रफल तथा समलम्ब चतुर्भुज BPQC के क्षेत्रफल का अनुपात ज्ञात कीजिए |
View Solutionदो समरूप त्रिभुजों के क्षेत्रफल क्रमशः 100 सेमी`""^(2)` तथा 64 सेमी`""^(2)` है | यदि छोटे त्रिभुज की माध्यिका 5.6 सेमी है | तो दूसरे की संगत मध्यिका ज्ञात कीजिए |
View Solution`triangle ABC,A` पर समकोण है तथा `ADbot BC` है | यदि BC = 13 सेमी और AC = 5 सेमी है तो `triangle ABC` तथा `triangle ADC` के क्षेत्रफल का अनुपात ज्ञात कीजिए |
View Solution
अभ्यास प्रश्न 7.3 questions and complete solutions for chapter त्रिभुज of SHREE BALAJI MATHS (HINDI) of Class 10