Complete Solutions to स्वमूल्यांकन परीक्षण of chapter त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | त्रिभुज |
| BALAJI PUBLICATION | स्वमूल्यांकन परीक्षण |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
सिद्ध कीजिए की समचतुर्भुज की भुजाओं के वर्गो का योग, इसके विकर्णो के वर्ग के योग के बराबर होता है |
View Solutionएक समबाहु त्रिभुज की भुजा `3sqrt(3)` सेमी है | शीर्षलम्ब की लम्बाई ज्ञात कीजिए |
View Solutionएक समलम्ब चतुर्भुज PQRS के विकर्ण बिंदु O पर प्रतिच्छेद करते है | `PQ||RS` तथा PQ = 3RS तब `triangle POQ` व `triangle ROS` के क्षेत्रफलो का अनुपात ज्ञात कीजिए |
View Solutionगली के स्तर से 6 मीटर ऊपर लगे खम्बे पर एक बल्ब लगा है | यदि एक महिला जिसकी ऊंचाई 1.5 मीटर है, की परछाई 3 मीटर है | खम्बे के आधार से महिला की दूरी ज्ञात कीजिए |
View Solutionसलंग्न चित्र 7.146 में, यदि `AB||DC` तथा AC व PQ परस्पर बिंदु O पर प्रतिच्छेद करते है सिद्ध कीजिए की `CQ = OC * AP`
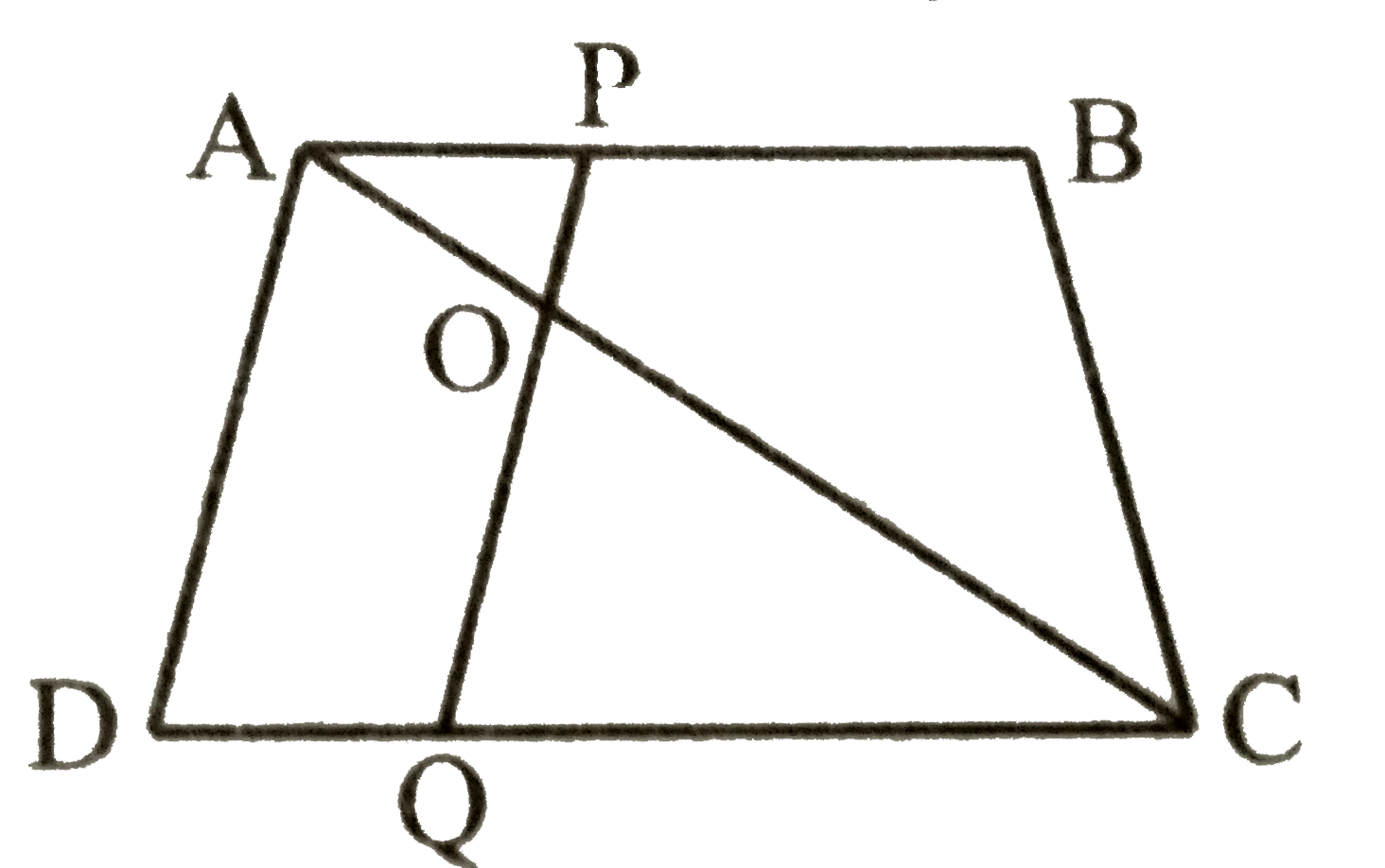
View Solution`triangle PQR` में, `PD bot QR` इस प्रकार है कि D, QR पर स्थित है | यदि PQ = a, PR = b,QD = c तथा DR = d, तो सिद्ध कीजिए कि `(a+b)(a-b) = (c+d)(c-d)`
View Solutionशहर A से, शहर C के द्वारा शहर B तक पहुँचने का मार्ग इस प्रकार है कि `AC bot CB,` AC = 2x किमी० तथा `CB = 2(x+7)`किमी० A व B को सीधे जोड़ने के लिए 26 किमी० का हाइवे बनाने का प्रस्ताव है | हाइवे बनने पर A से B तक पहुँचने में कितनी दुरी कम होगी |
View Solutionदो त्रिभुज ABC व DBC, आधार एक के एक और बने है | BC पर किसी बिंदु P से, `PQ ||AB` तथा `PR||BD` इस प्रकार खींचे गये है कि वे AC पर बिंदु Q तथा DC पर बिंदु R पर मिलते है | सिद्ध कीजिए कि `QR||AD`
View Solutionएक चतुर्भुज ABCD में, `angle ABC` व `angle ADC` के अर्द्धक विकर्ण AC पर मिलते है | सिद्ध कीजिए कि `angleBAD` व `angleBCD` के अर्द्धक, विकर्ण BD पर मिलते है |
View Solutionएक त्रिभुज `triangle ABC` में, BD व CE दो ऊँचाइयाँ है सिद्ध कीजिए कि `triangle ADB` व `triangle AEC` समरूप है, जहां BD = CE
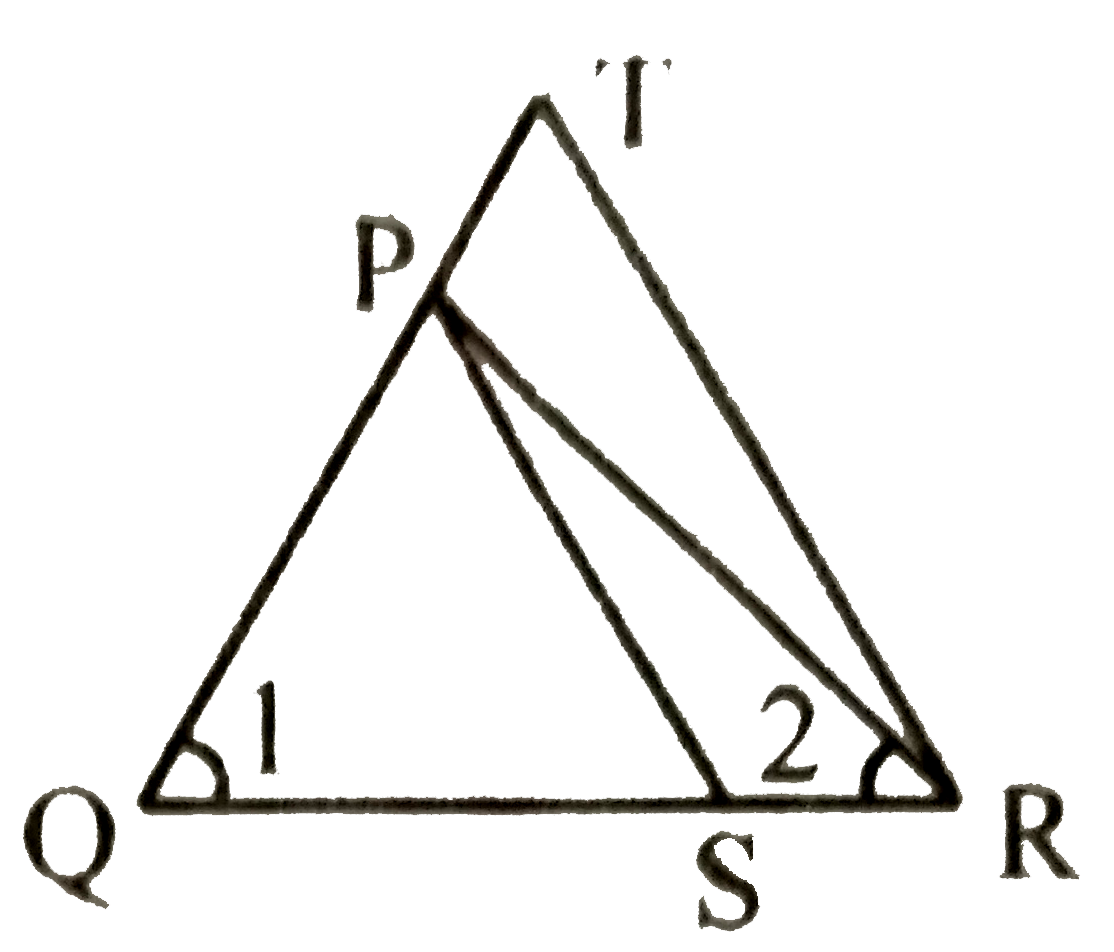
View Solutionदिये गये चित्र में, यदि `(QT)/(PR) = (QR)/(QS)` तथा `angle 1 = angle2` सिद्ध कीजिए कि `triangle PQS ~ triangle TQR`
View Solutionसिद्ध कीजिए कि त्रिभुज की भुजाओं के मध्य बिंदुओं को मिलाने वाली रेखा ऐसे चार त्रिभुज बनती है जो दिये गये त्रिभुज के समरूप है |
View Solution`triangle ABC` के एक अन्तः बिंदु O से, भुजा BC,CA तथा AB पर लम्ब क्रमशः OD,OE व OF खींचे गये है | सिद्ध कीजिए कि
(i) `AF^(2) + BD^(2) + CE^(2) = OA^(2) + OB^(2) + OC^(2) - OD^(2) - OE^(2) - OF^(2)`
(ii) `AF^(2) + BD^(2) + CE^(2) = AE^(2) + CD^(2) + BF^(2)`
View Solutionकिसी `triangle ABC` में, D, भुजा BC का मध्य बिंदु इस प्रकार है कि `(BD)/(DC) = (AB)/(AC)` सिद्ध कीजिए कि AD, `angleA` का अर्द्धक है |
View Solutionएक समान्तर चतुर्भुज ABCD में, P, DC का मध्य बिंदु है तथा एक बिंदु Q भुजा एक पर इस प्रकार है कि `CQ = (1)/(4)AC` अब PQ को बढ़ाने पर यह BC से बिंदु R पर मिलती है तो सिद्ध कीजिए कि R भुजा BC का मध्य बिंदु है |
View Solution7.5 मीटर लम्बी एक छड़ी की परछाई 5 मीटर लम्बी है | उसी समय एक मीनार की परछाई 24 मीटर है | मीनार की ऊँचाई ज्ञात कीजिए |
View Solution7.5 मीटर लम्बी एक छड़ी की परछाई 5 मीटर लम्बी है| उसी समय एक मीनार की परछाई 24 मीटर है | मीनार की ऊंचाई ज्ञात कीजिए |
View Solutionएक `triangle ABC` में, AB = AC, तथा BC को D तक बढ़ाये तब सिद्ध कीजिए कि `AD^(2) - AC^(2) = BD * CD`
View Solution
स्वमूल्यांकन परीक्षण questions and complete solutions for chapter त्रिभुज of SHREE BALAJI MATHS (HINDI) of Class 10