Complete Solutions to उदाहरण of chapter त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | त्रिभुज |
| BALAJI PUBLICATION | उदाहरण |
| Number Of Questions | 97 |
| Academic Year | 2023-24 |
दी गई आकृति में `EF||AB||CD` है तो सिद्ध कीजिए कि
`(AE)/(ED) = (BF)/(FC)`
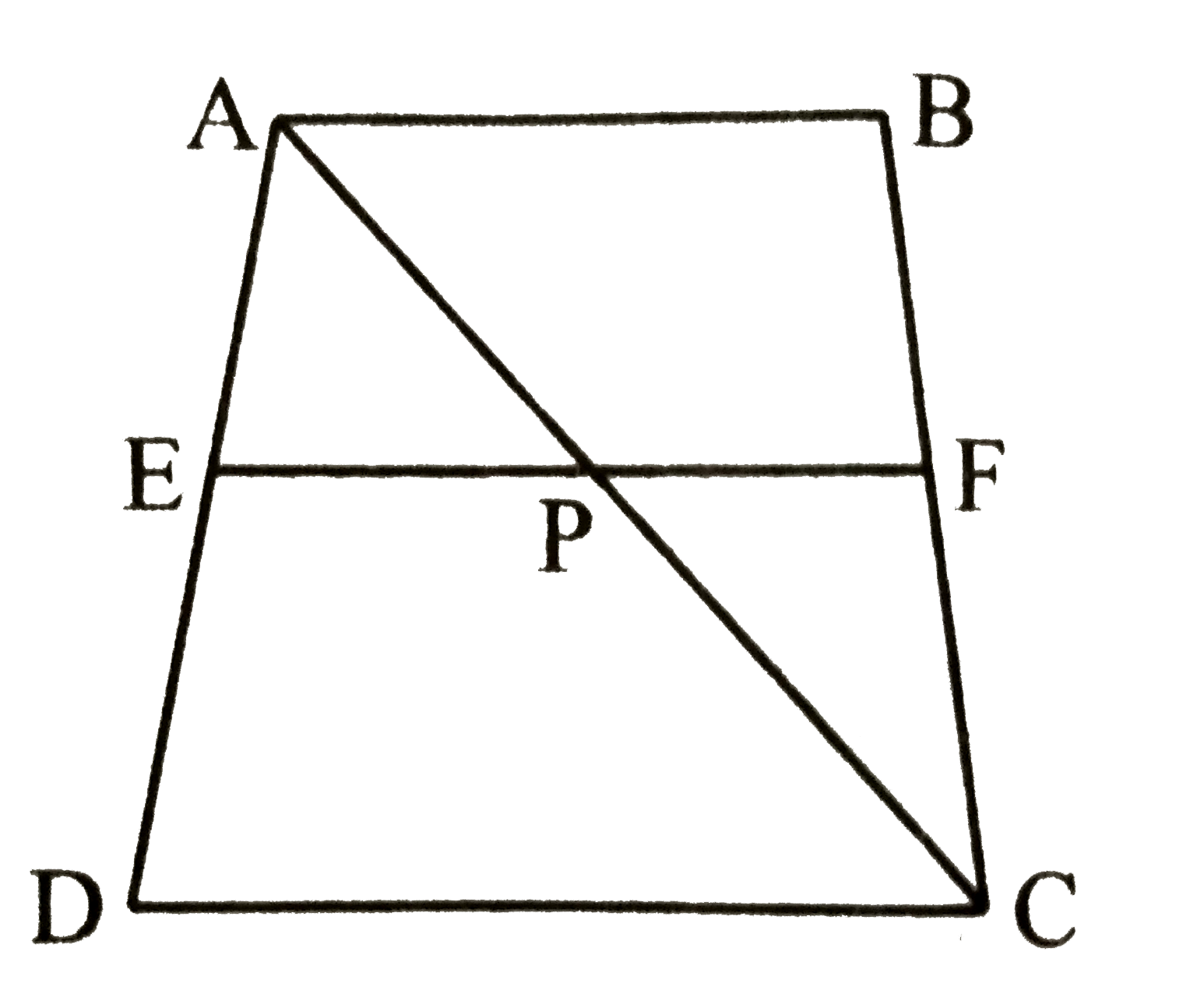
View Solutionदी गई आकृति में, `DE।।BC` तथा `CD।।EF` तो सिद्ध कीजिए
`AD^(2) = AB xx AF`
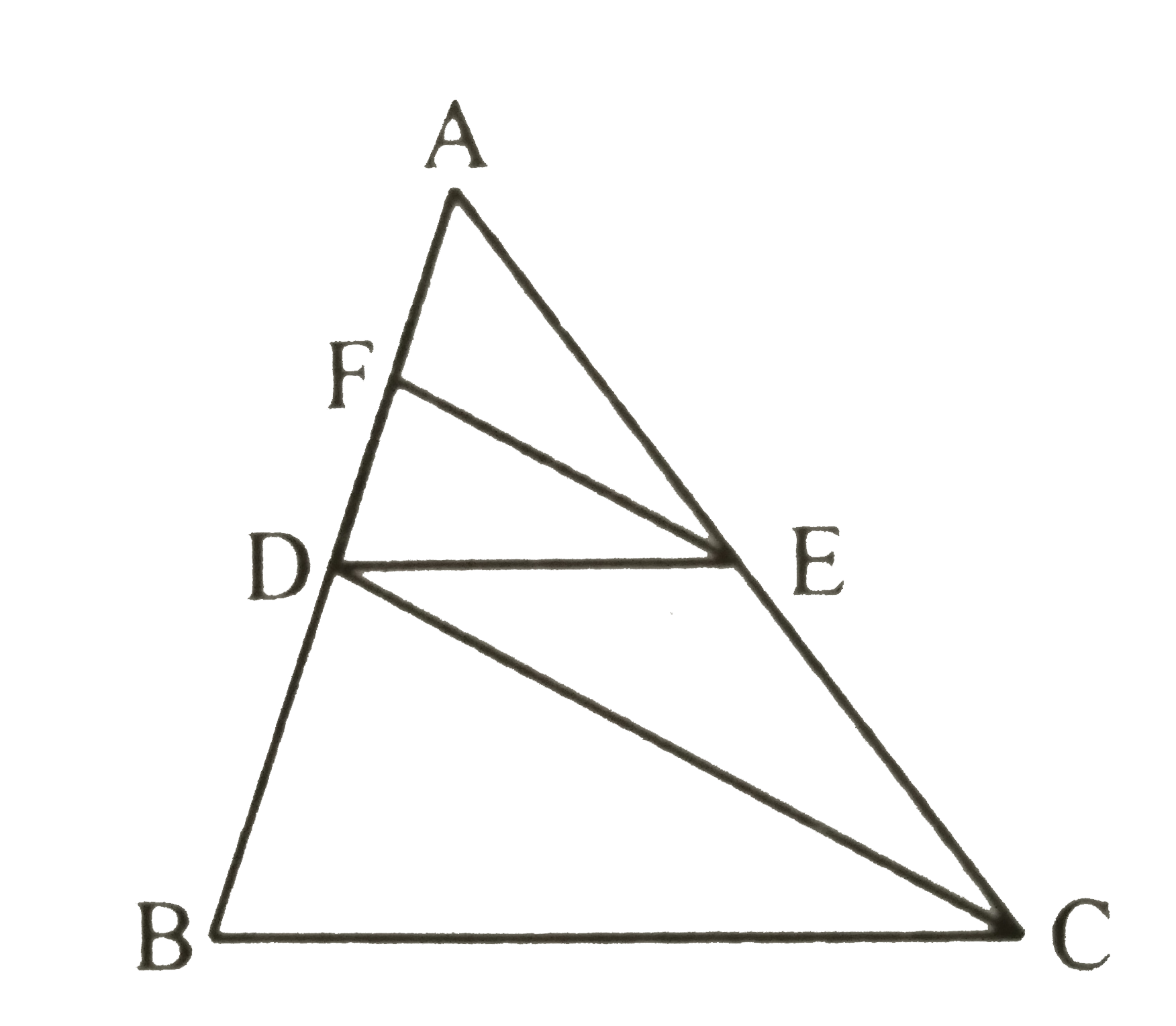
View Solutionदी गई आकृति में `DE||AC` तथा `DC||AP` है तो सिद्ध कीजिए कि
`(BE)/(EC) = (BC)/(CP)`
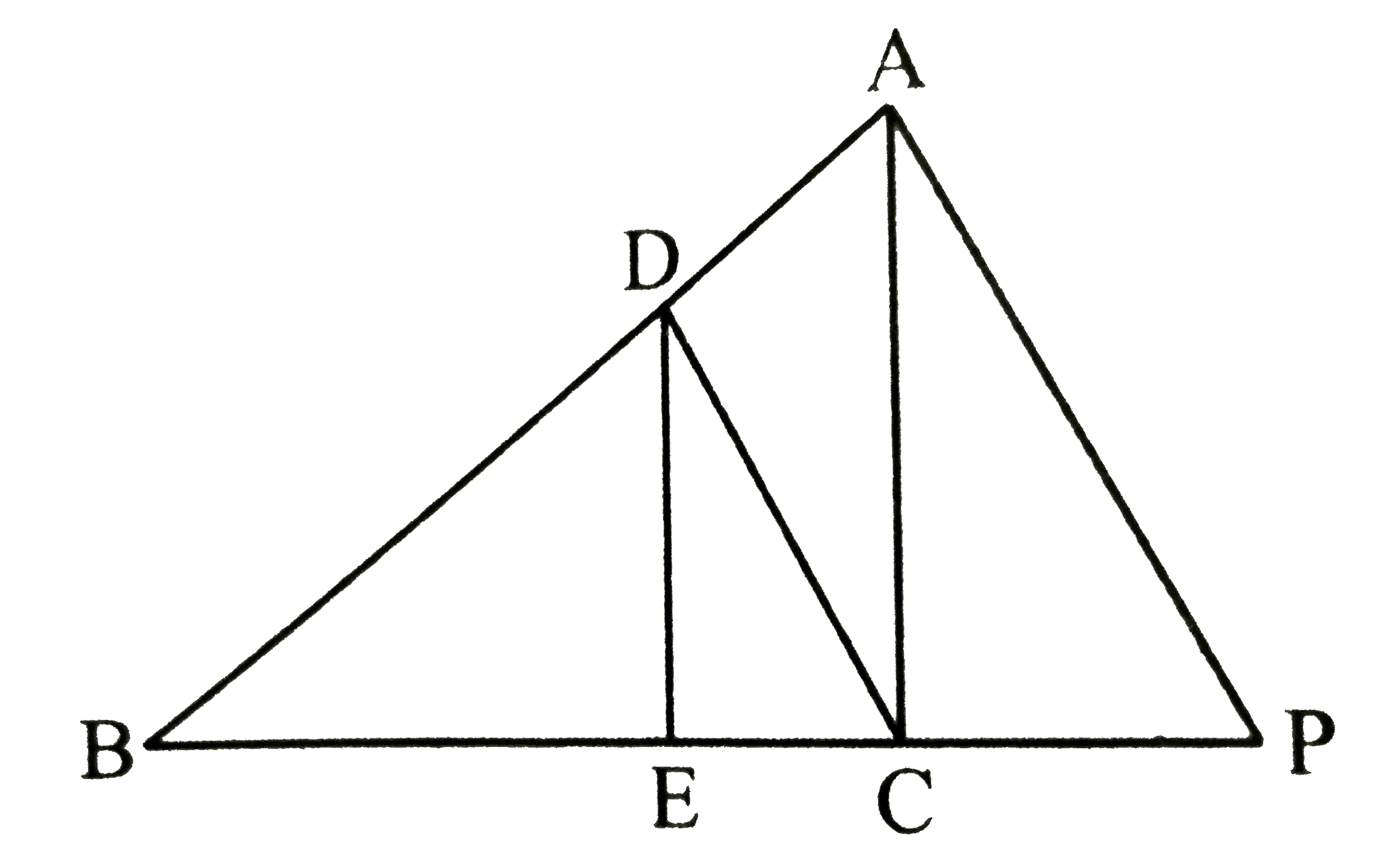
View Solutionदी गई आकृति में `PQ ।।BC` तथा `PR।।CD` है । तो सिद्ध कीजिए कि
(i) `(AR)/(AD) = (AQ)/(AB)`
(ii) `(QB)/(AQ) = (DR)/(AR)`
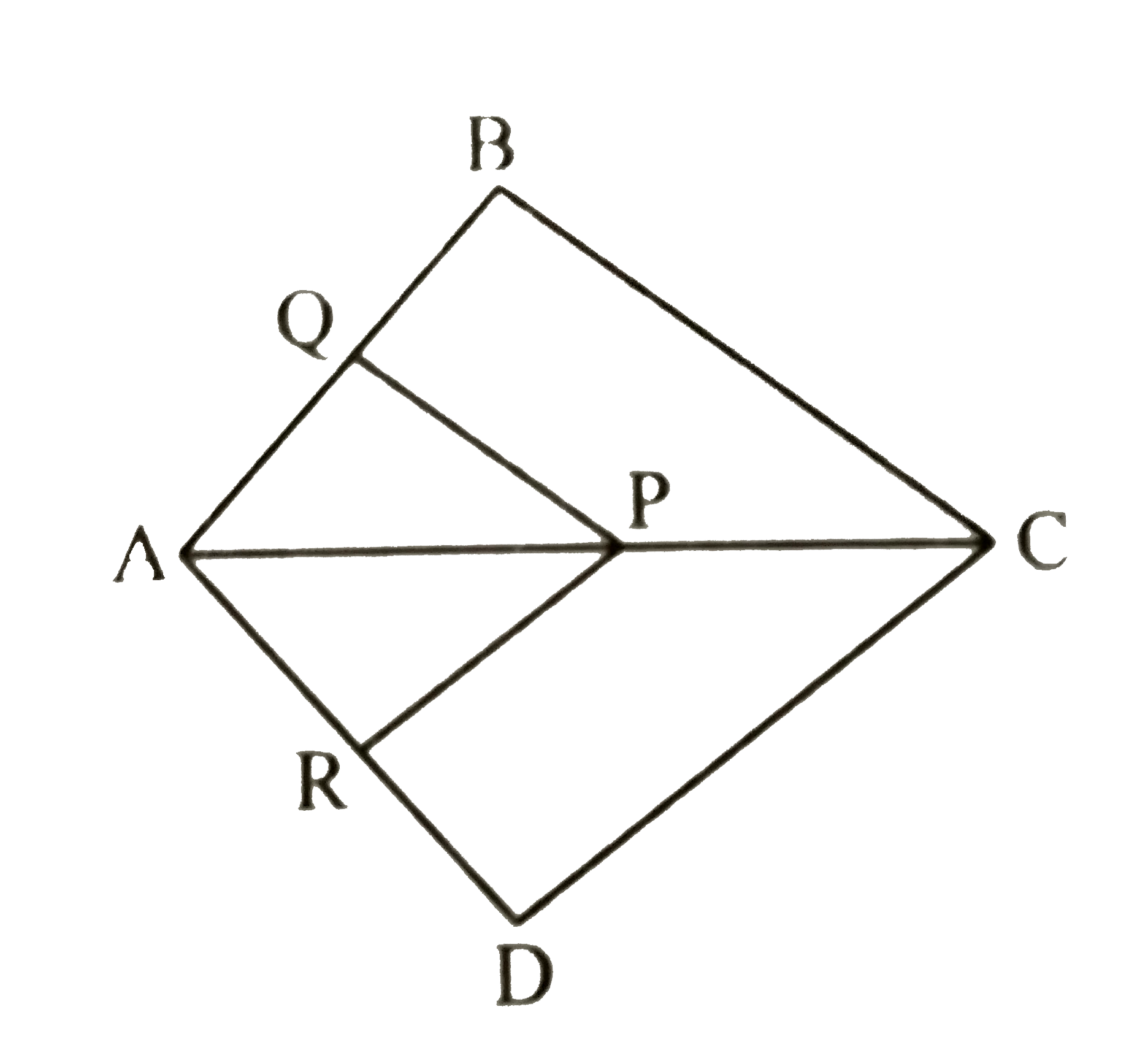
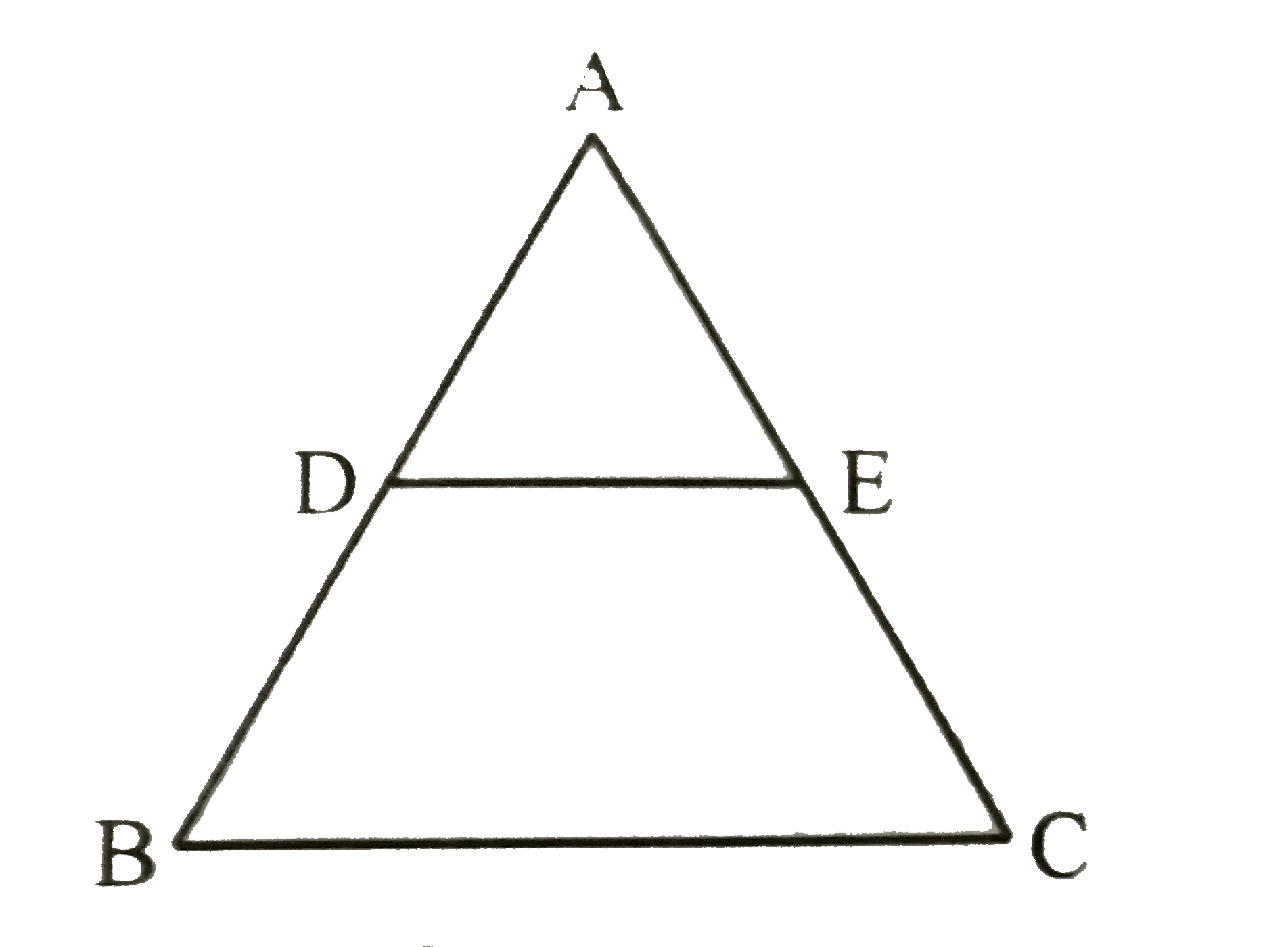
View Solutionदी गई आकृति में `DE।।BC` तथा `(AD)/(DB) = (3)/(5)` है यदि AC = 4.8 सेमी है तो AE ज्ञात कीजिए ।
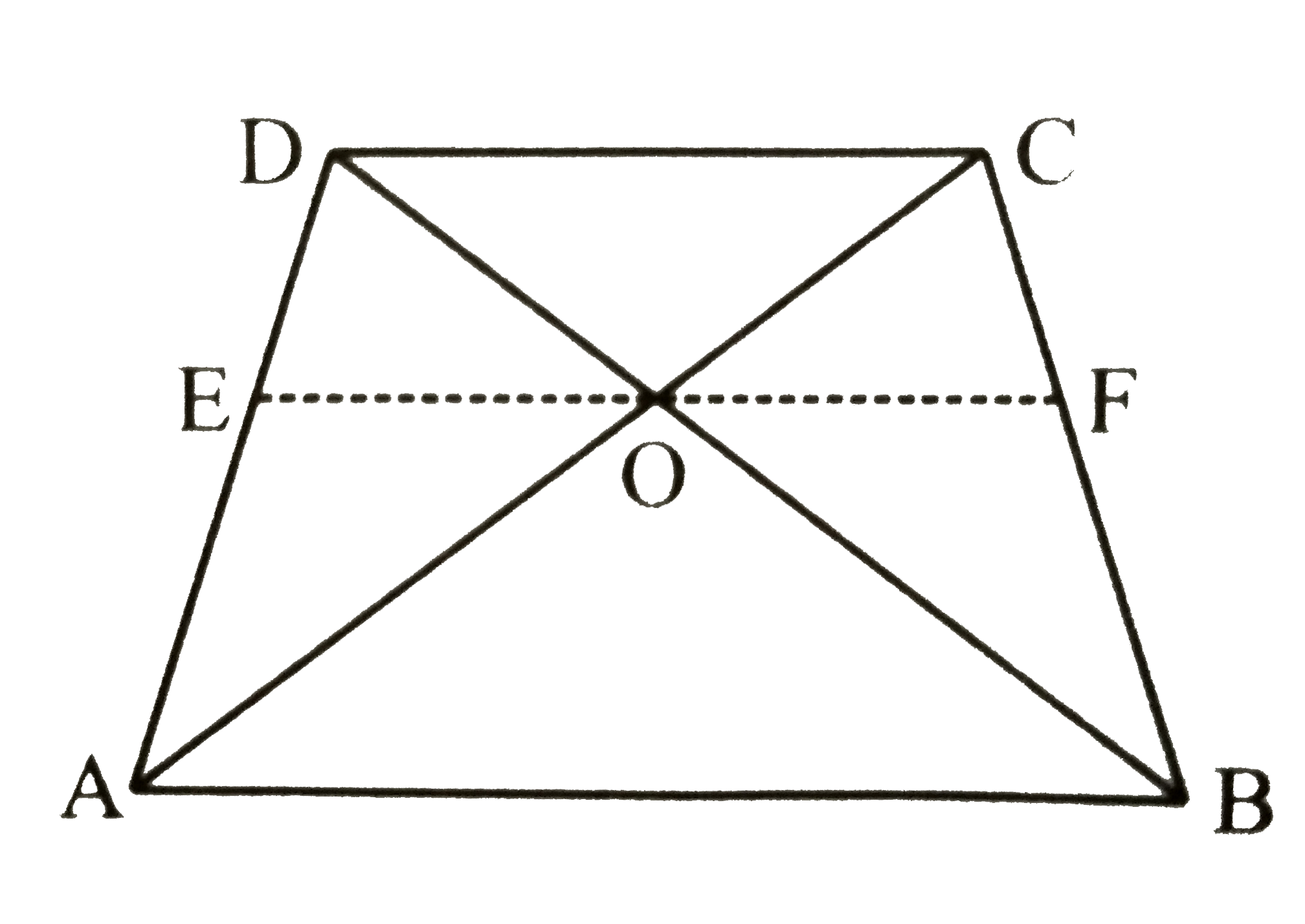
View Solutionदी गई आकृति में AB, CD के समान्तर है । यदि `OA = 3x -19, OB = x-4`,
`OC = x-3` तथा `OD = 4` है तो x का मान ज्ञात कीजिए ।
View SolutionABCD एक समलम्भ चतुर्भुज है जिसमे `AB||DC` और इसके विकर्ण एक-दूसरे को एक बिंदु O पर प्रतिच्छेद करते है दिखाइये कि, `(AO)/(BO) = (CO)/(DO)`
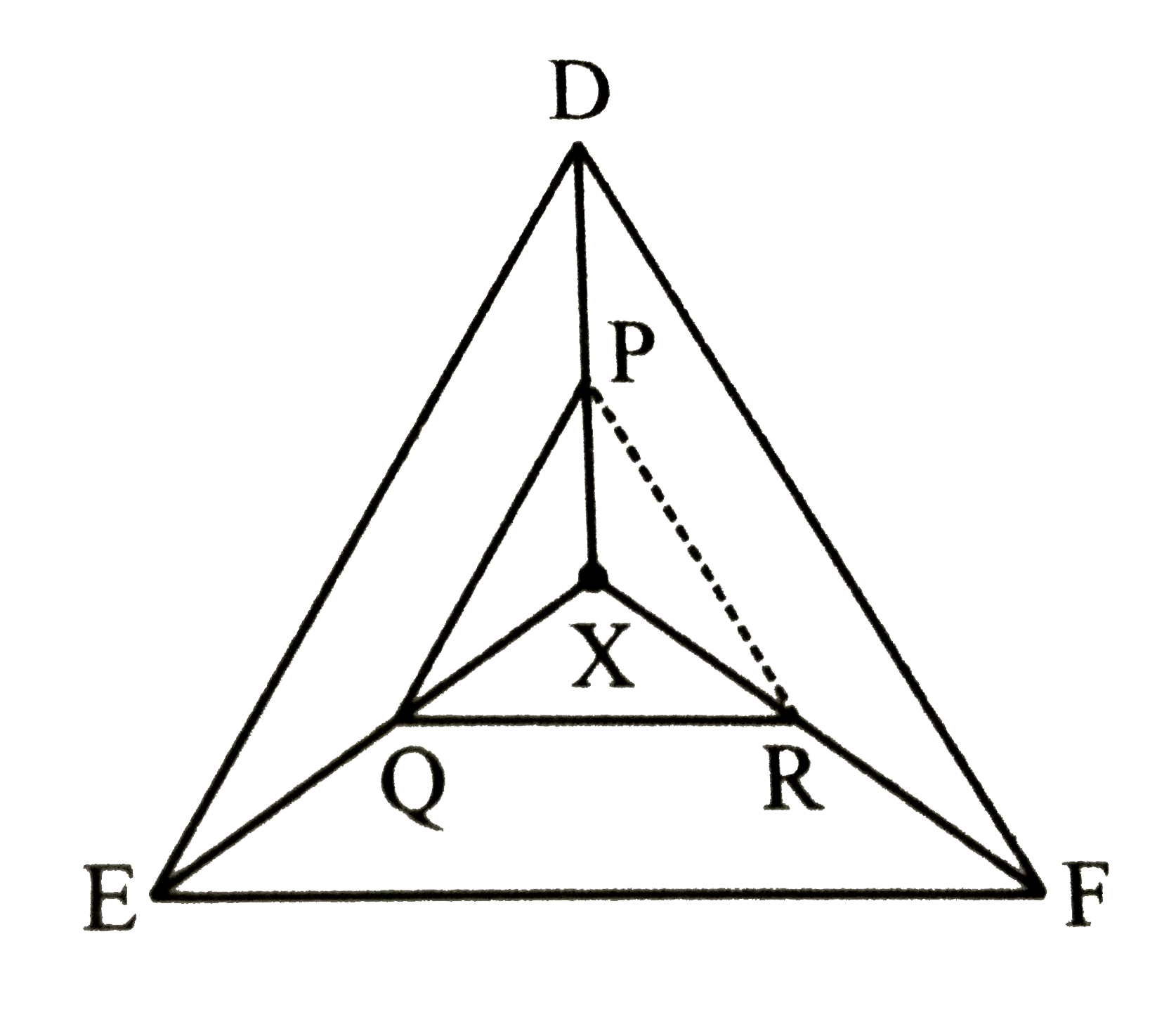
View Solution`triangleDEF` में कोई बिंदु X है जिसे शीर्ष D,E तथा F से मिलाया गया है । DX पर कोई P लेकर, `PQ।।DE` खींचा गया है, जो XE से Q पर मिलती है तथा `QR।।EF` जो XF से R मिलती है । सिद्ध कीजिए कि `PR।।DF`
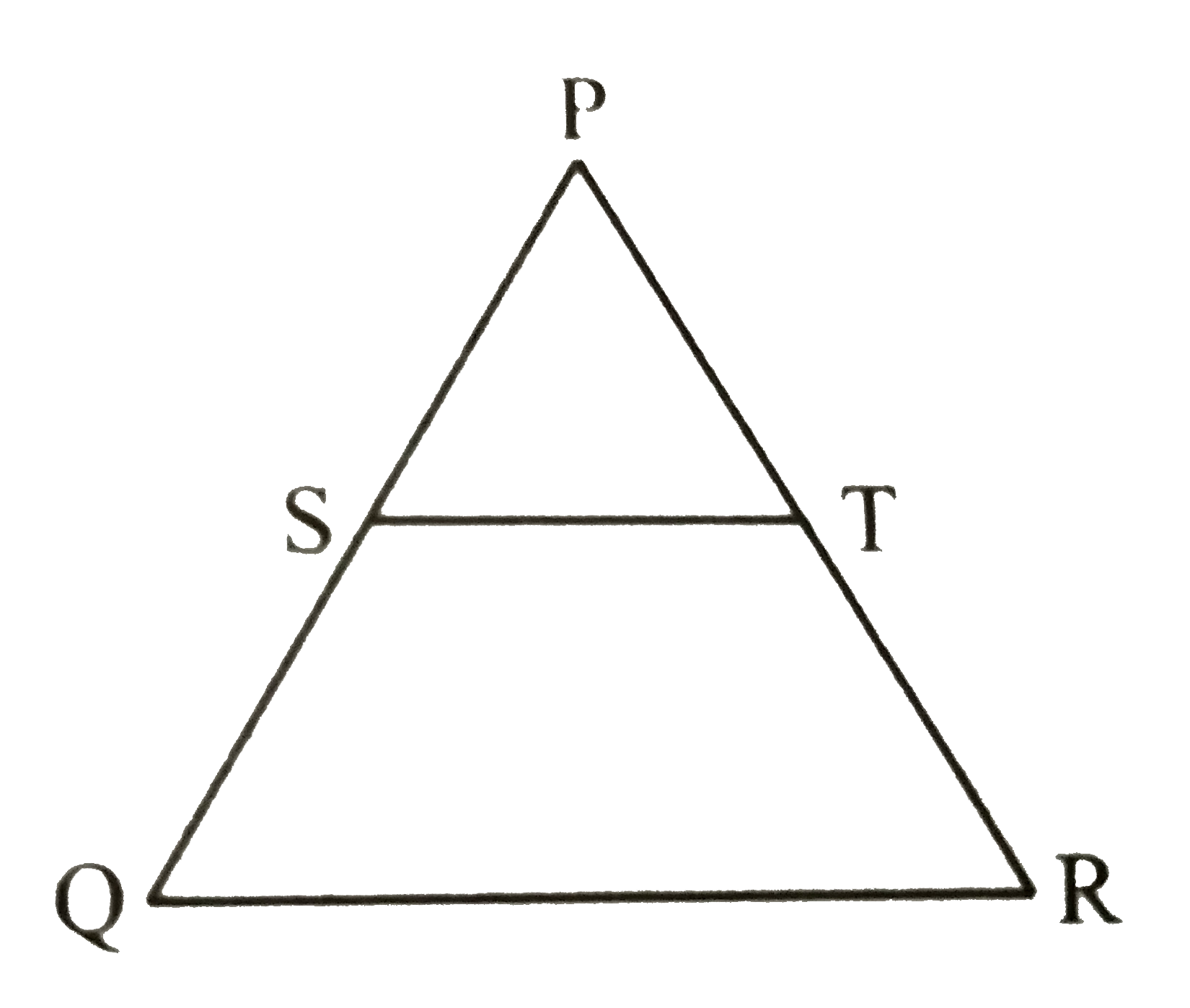
View Solutionदी गई आकृति में `(PS)/(SQ) = (PT)/(TR)` तथा `anglePST = anglePRQ` है । सिद्ध कीजिए कि
`trianglePQR` एक समद्विबाहु त्रिभुज है ।
View Solutionदी गई आकृति में, यदि `DE||AQ` तथा `DF||AR` तो सिद्ध कीजिए कि `EF ||QR`
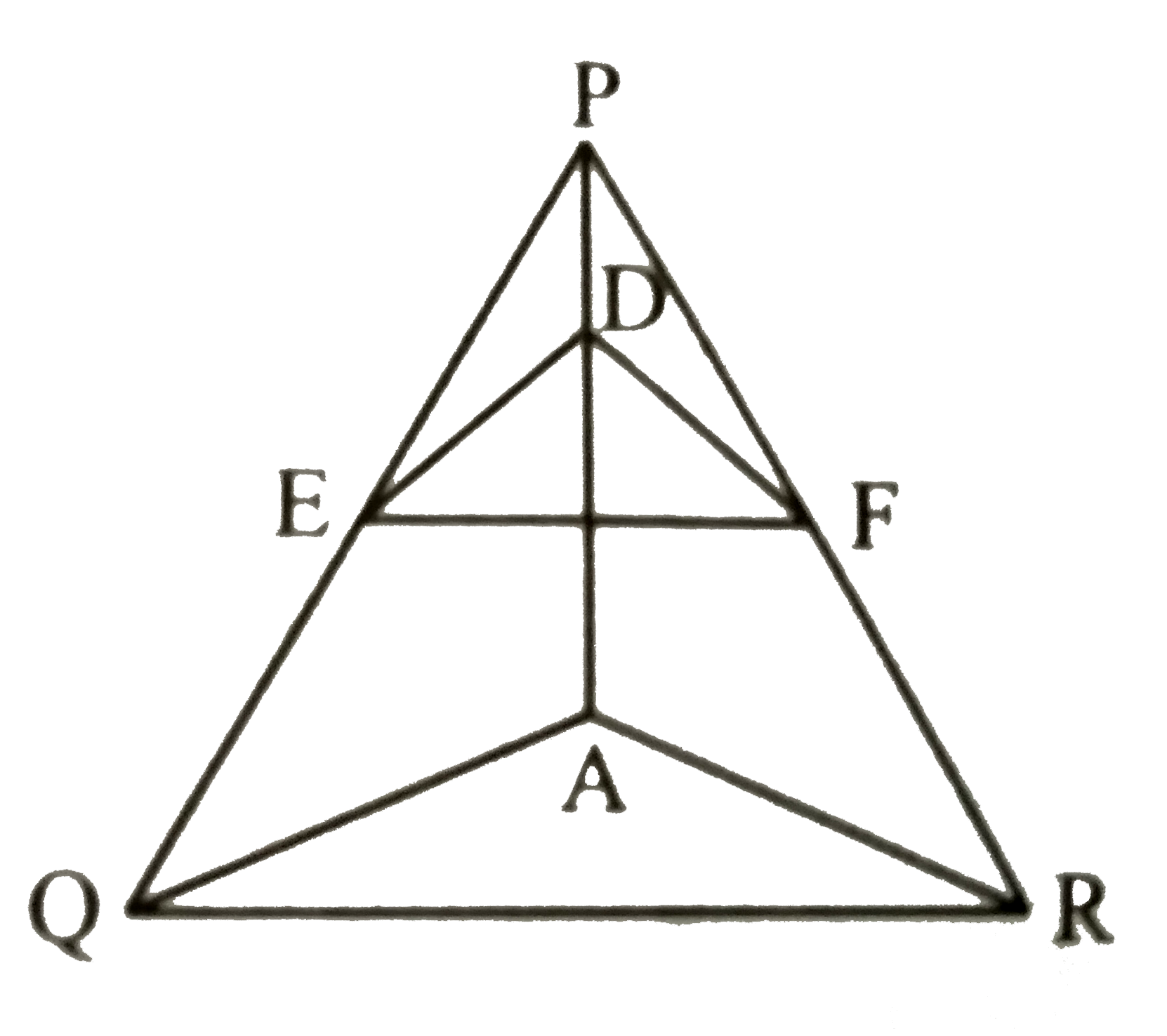
View Solutionदी गई आकृति में, PA, QB तथा RC, AC के लंबवत है । तथा `PA =x, RC = y, QB = z, AB =a` तथा BC =b तो सिद्ध कीजिए कि `(1)/(x) + (1)/(y)=(1)/(z)`
View Solutionदी गई आकृति में AD, `angle BAC` को दो भागो में बाटता है । यदि AB = 10 सेमी, AC = 6 सेमी तथा BC = 12 सेमी है तो BD तथा DC ज्ञात कीजिए ।
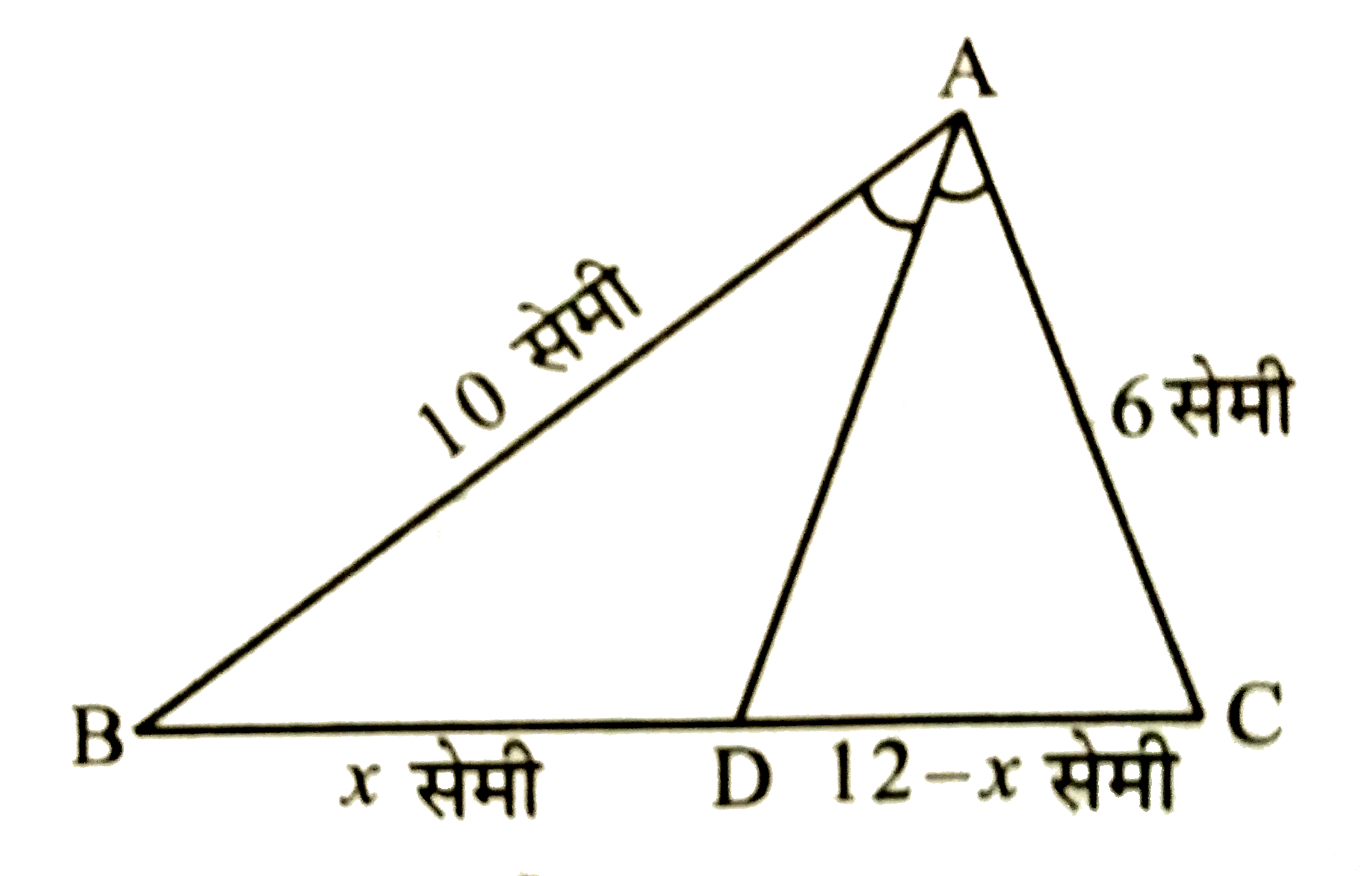
View Solutionयदि एक त्रिभुज के एक कोण का अर्द्धक, विपरीत भुजाओं का अर्द्धक है तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु है ।
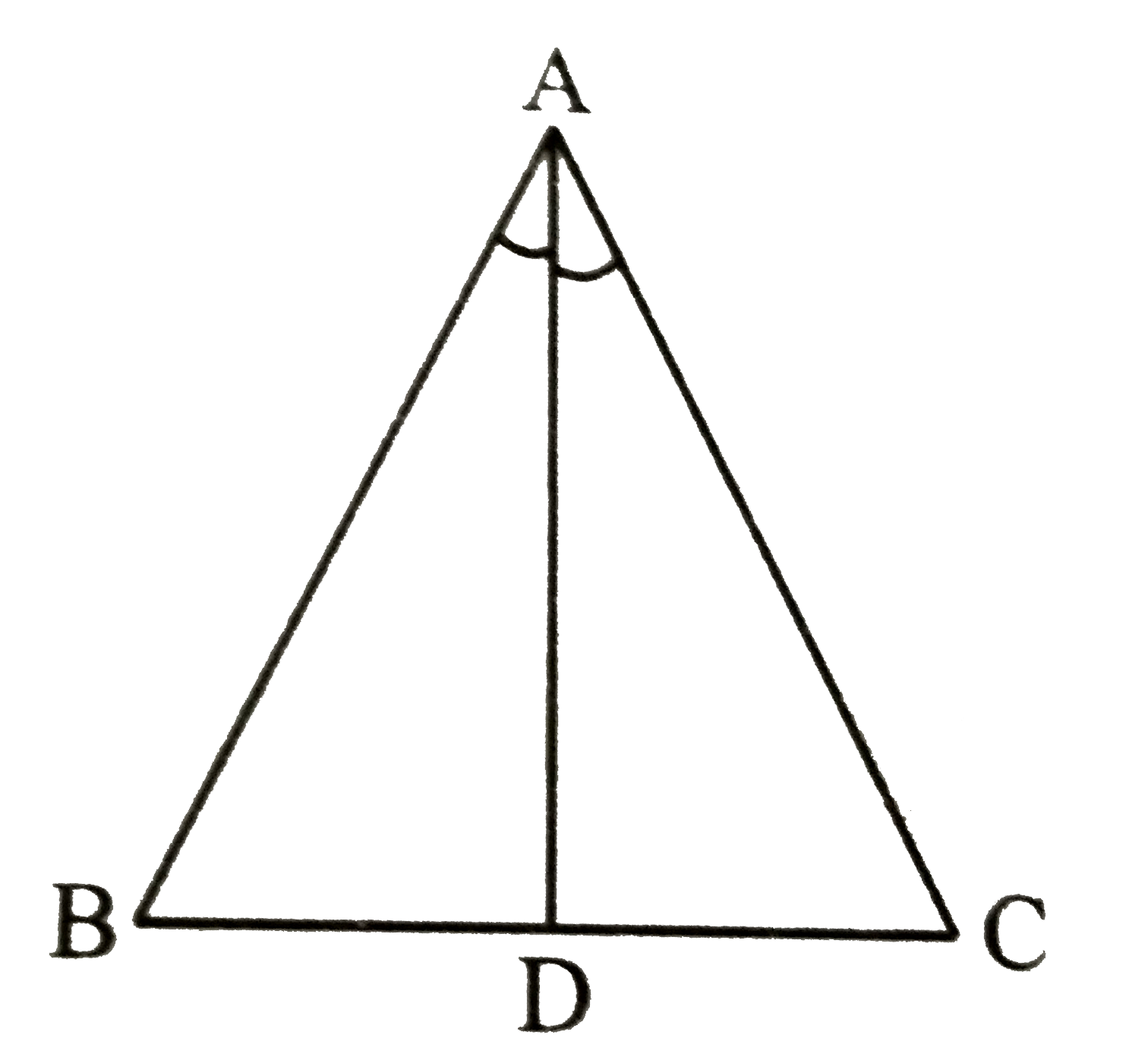
View Solutionएक त्रिभुज ABC का `angleB` तथा `angleC` का अर्द्धक विपरीत भुजा पर क्रमशः D तथा E में मिलता है । यदि `DE।।BC` तो सिद्ध कीजिए कि त्रिभुज समिद्विबाहु है ।
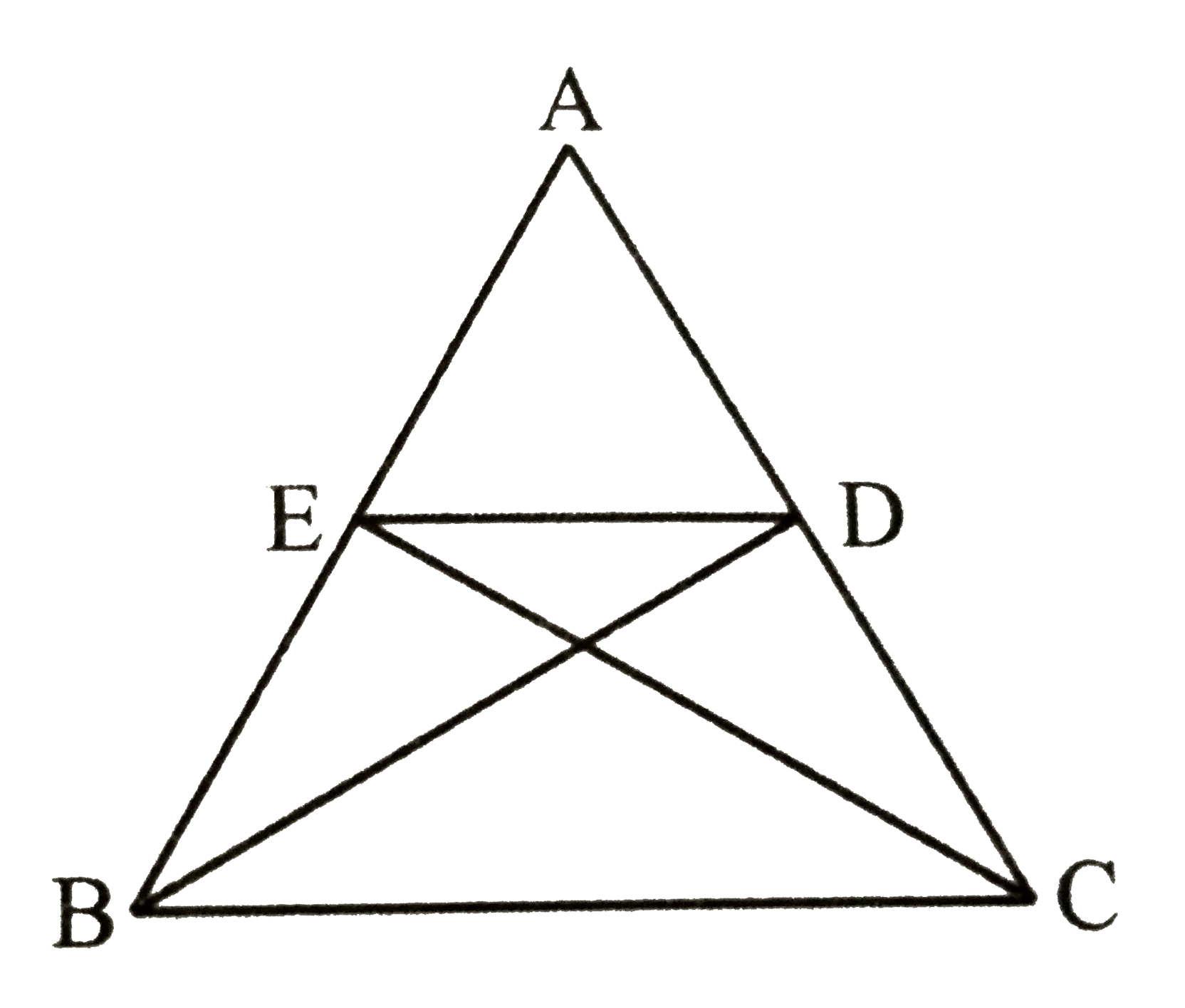
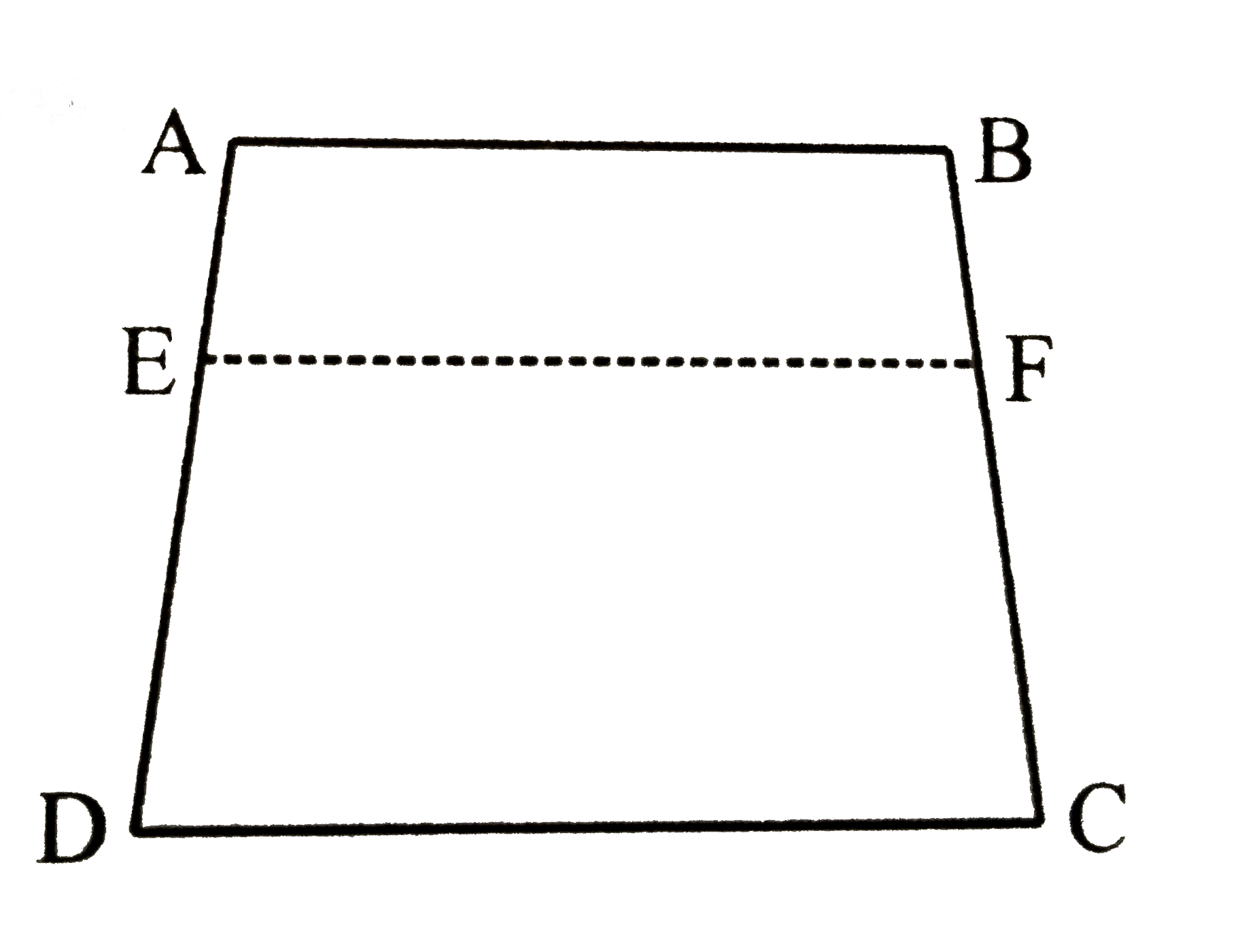
View SolutionABCD एक समलम्ब चतुर्भुज है । जहा `AB।।DC` बिन्दु E तथा F, क्रमशः असमान्तर भुजाओं AD तथा BC पर है तथा EF, AB के समान्तर है । तो सिद्ध कीजिए कि
`(AE)/(ED) = (BF)/(FC)`
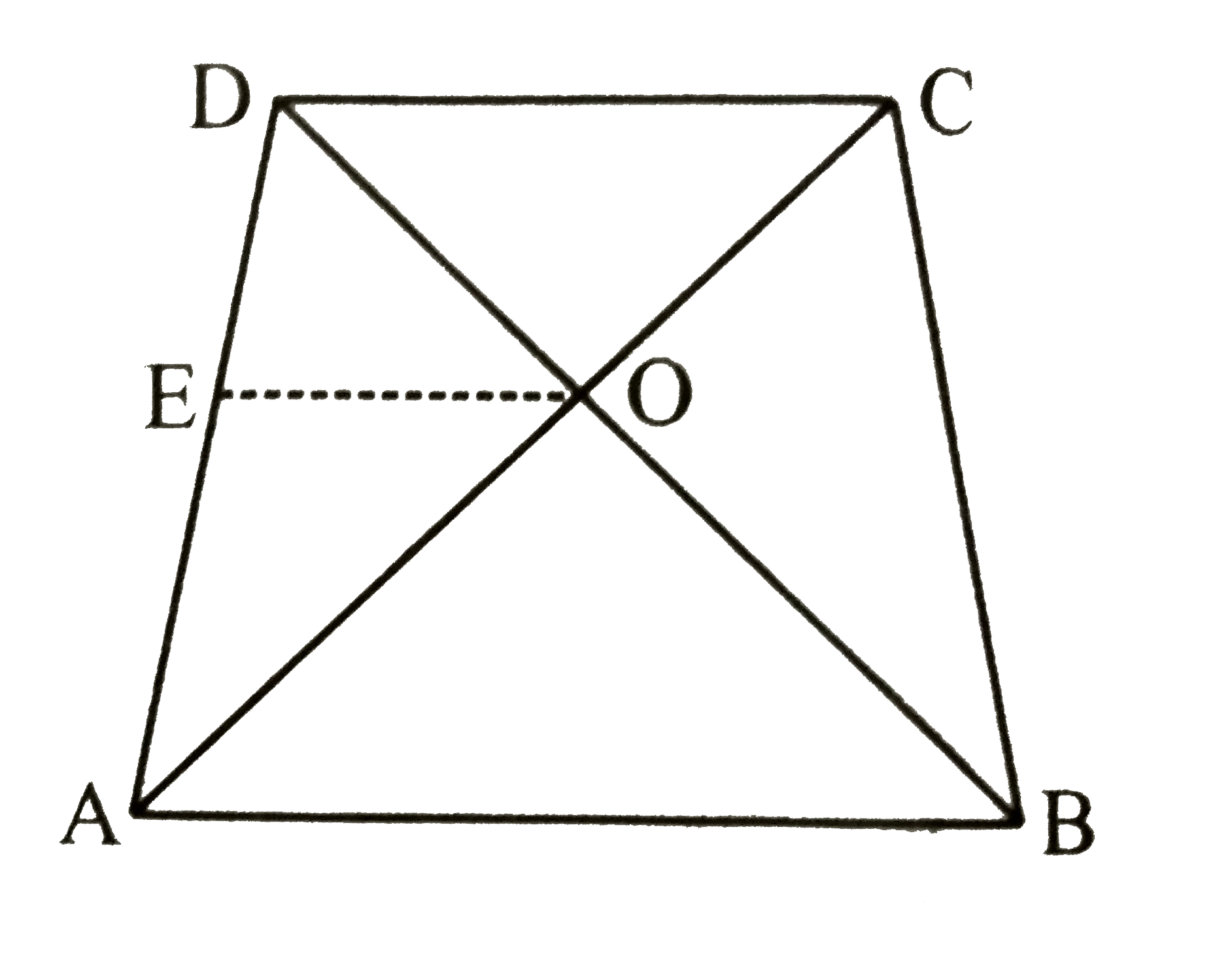
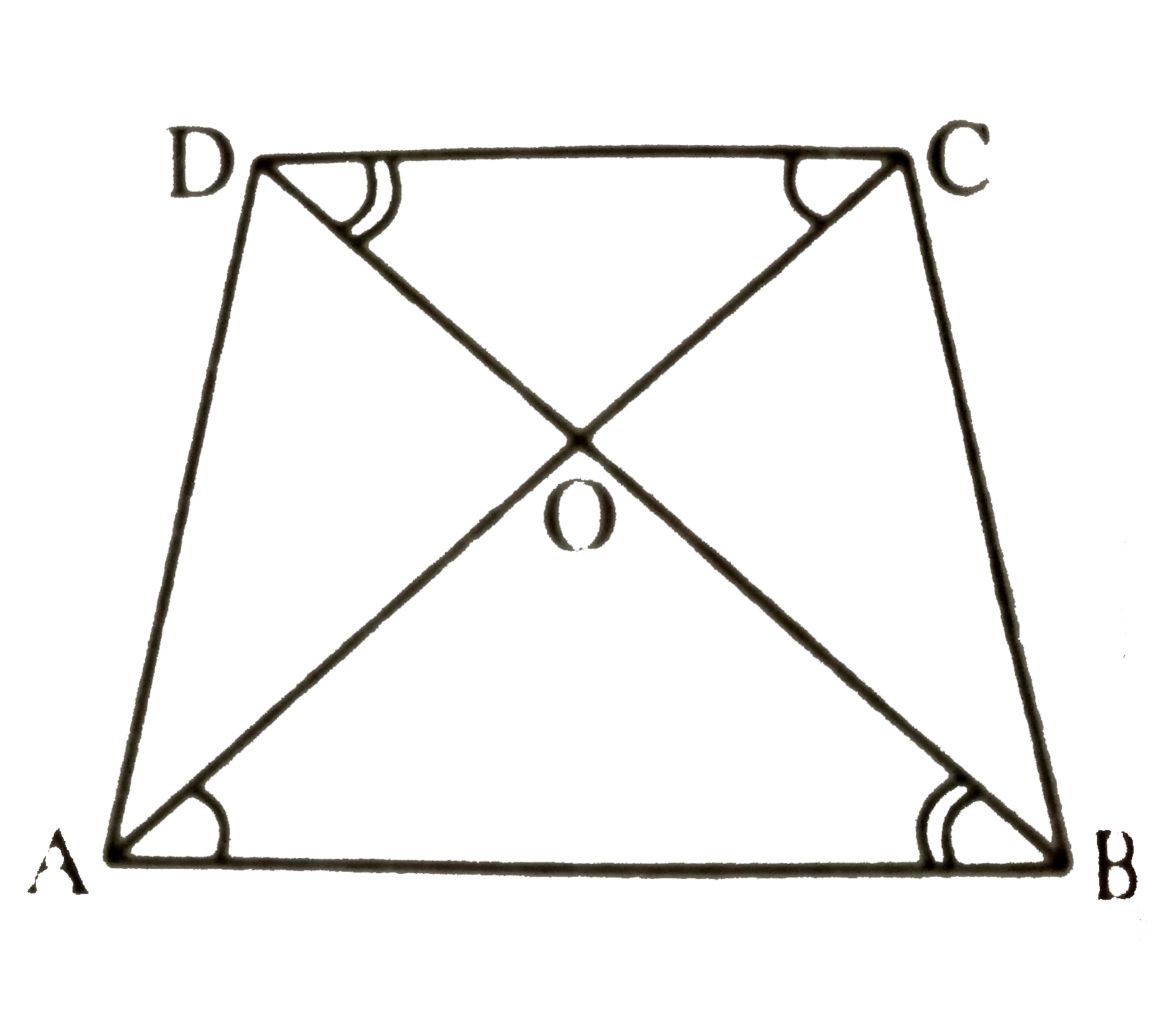
View Solutionचतुर्भुज ABCD के विकर्ण एक -दूसरे को बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि `(AO)/(BO) = (CO)/(DO)` तो सिद्ध कीजिए कि ABCD एक समलम्ब चतुर्भुज है ।
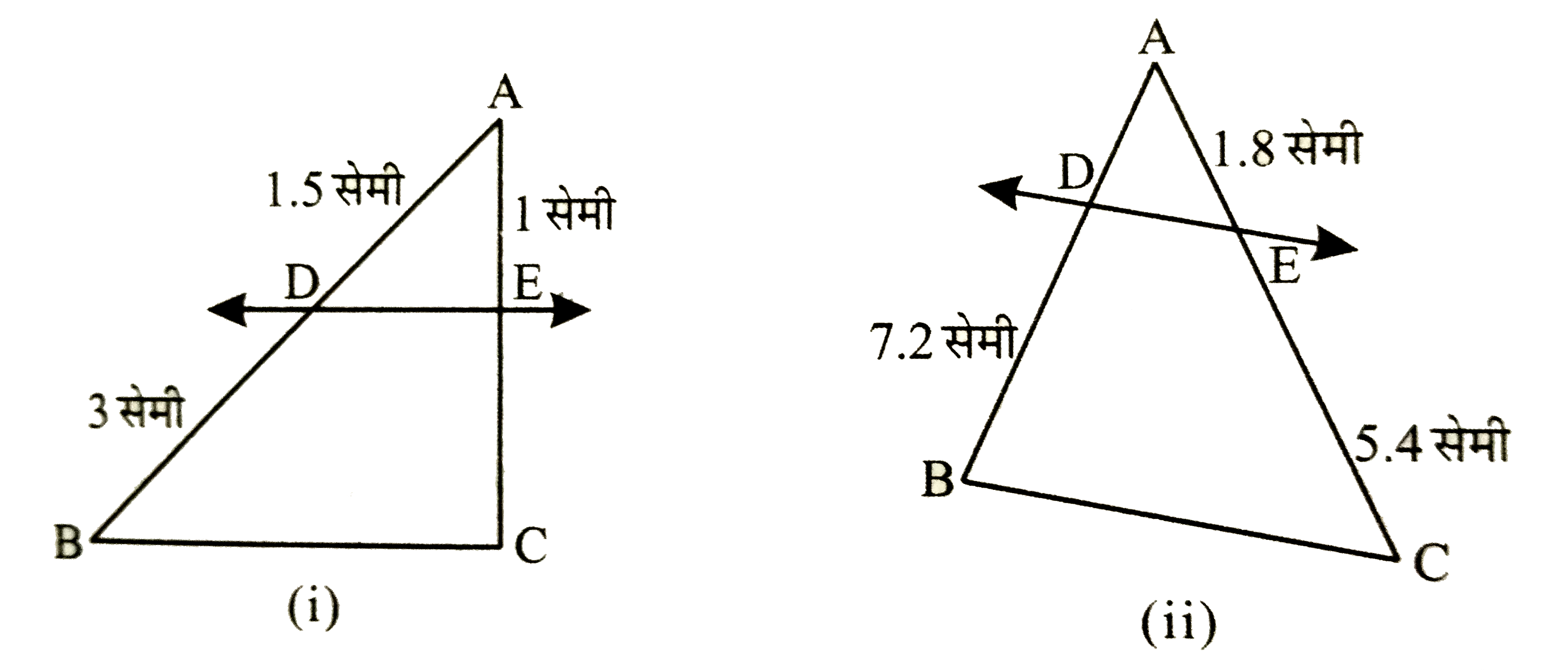
View Solutionदी गई निम्न (i) तथा (ii) आकृतियों में `DE।।BC`
(i) में EC ज्ञात कीजिए
में AD ज्ञात कीजिए ।
View Solution`trianglePQR` की भुजाओं PQ तथा PR पर क्रमशः बिंदु E तथा F है । निम्नलिखित प्रत्येक के लिए बताइये कि `EF।।QR` है या नहीं ।
(i) PE = 3.9 सेमी, EQ = 3.0 सेमी, PF = 3.6 सेमी, FR = 2.4 सेमी
(ii) PE = 4 सेमी, QE = 4.5 सेमी, PF = 8 सेमी, FR = 9.0 सेमी
(iii) PQ = 1.28 सेमी, PR = 2.56 सेमी, PE = 0.18 सेमी, PF = 0.36 सेमी
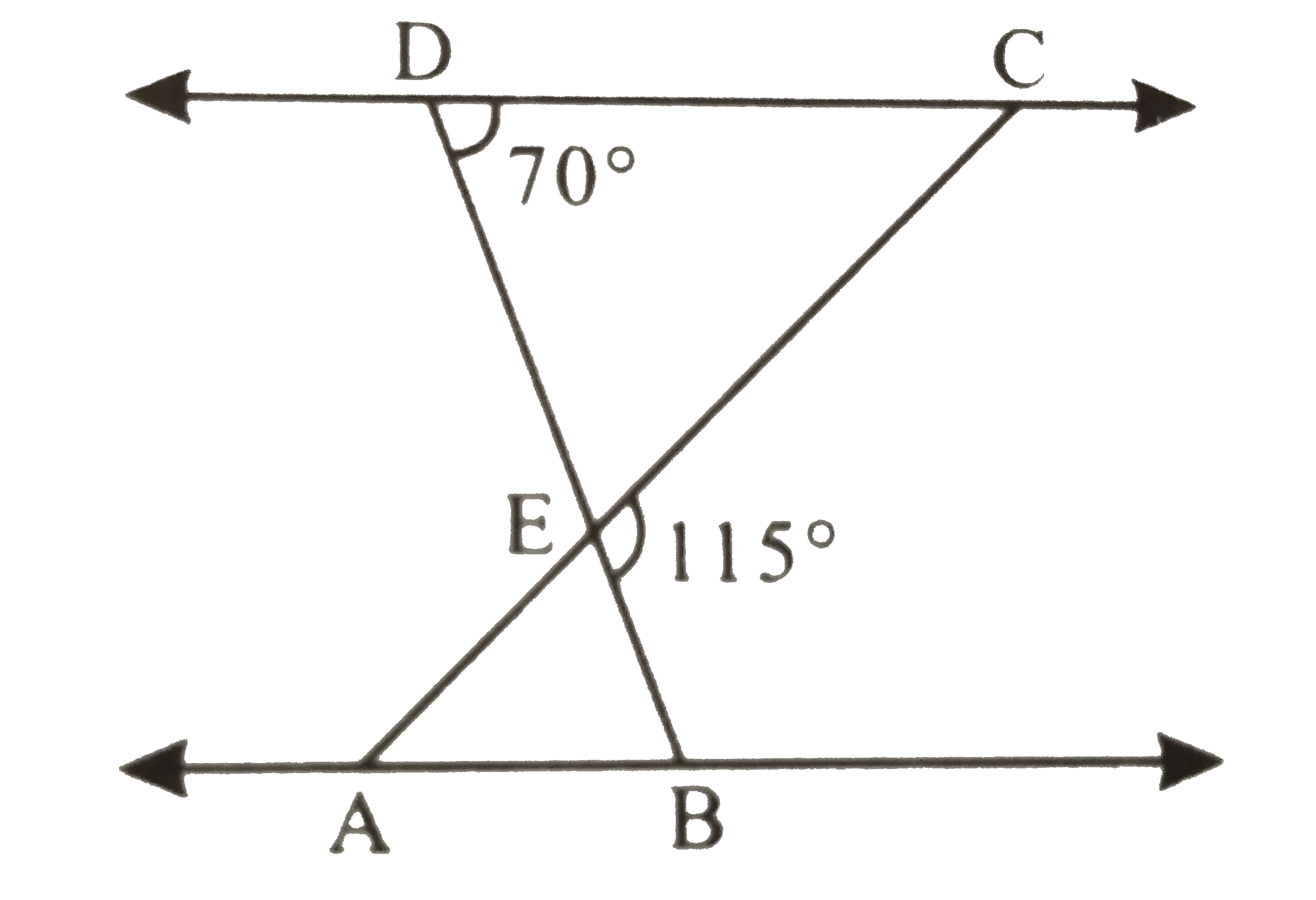
View Solutionदी गई आकृति में, यदि `triangleEDC` तथा `triangleEBA` समरूप है । `angleBEC = 115^(@)` तथा `angleEDC = 70^(@)` तब `angleDEC, angleDCE, angleEAB, angleAEB` तथा `angleEBA` ज्ञात कीजिए ।

View Solutionदी गई आकृतियों में `angleE` ज्ञात कीजिए ।
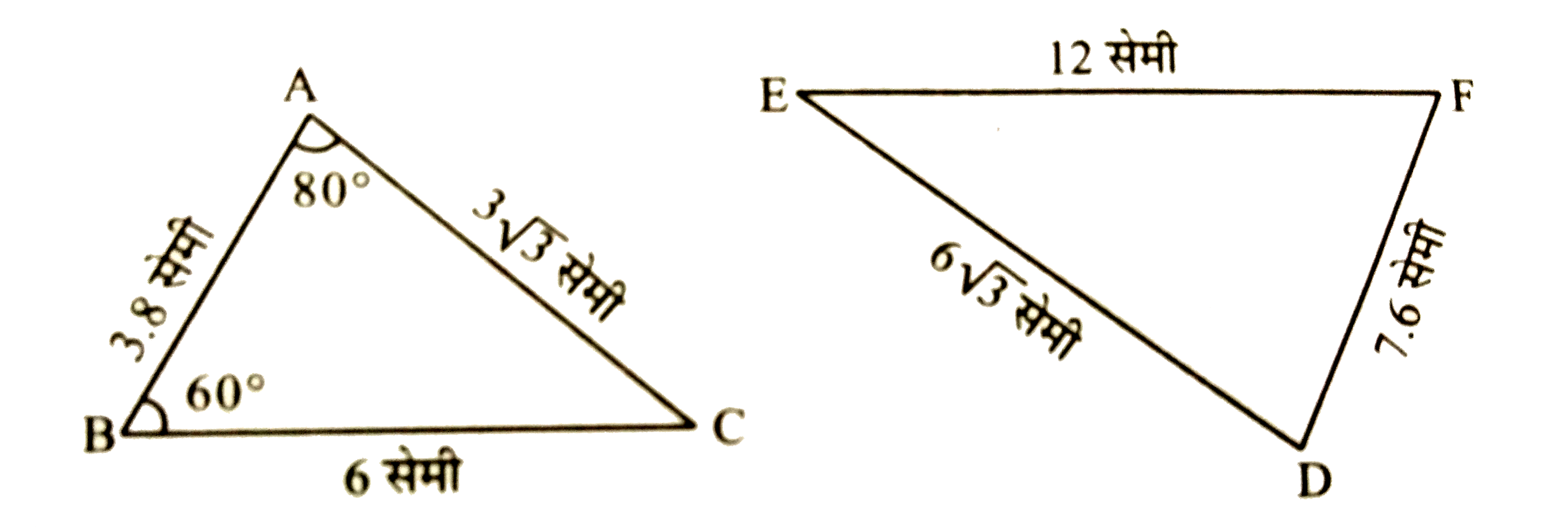
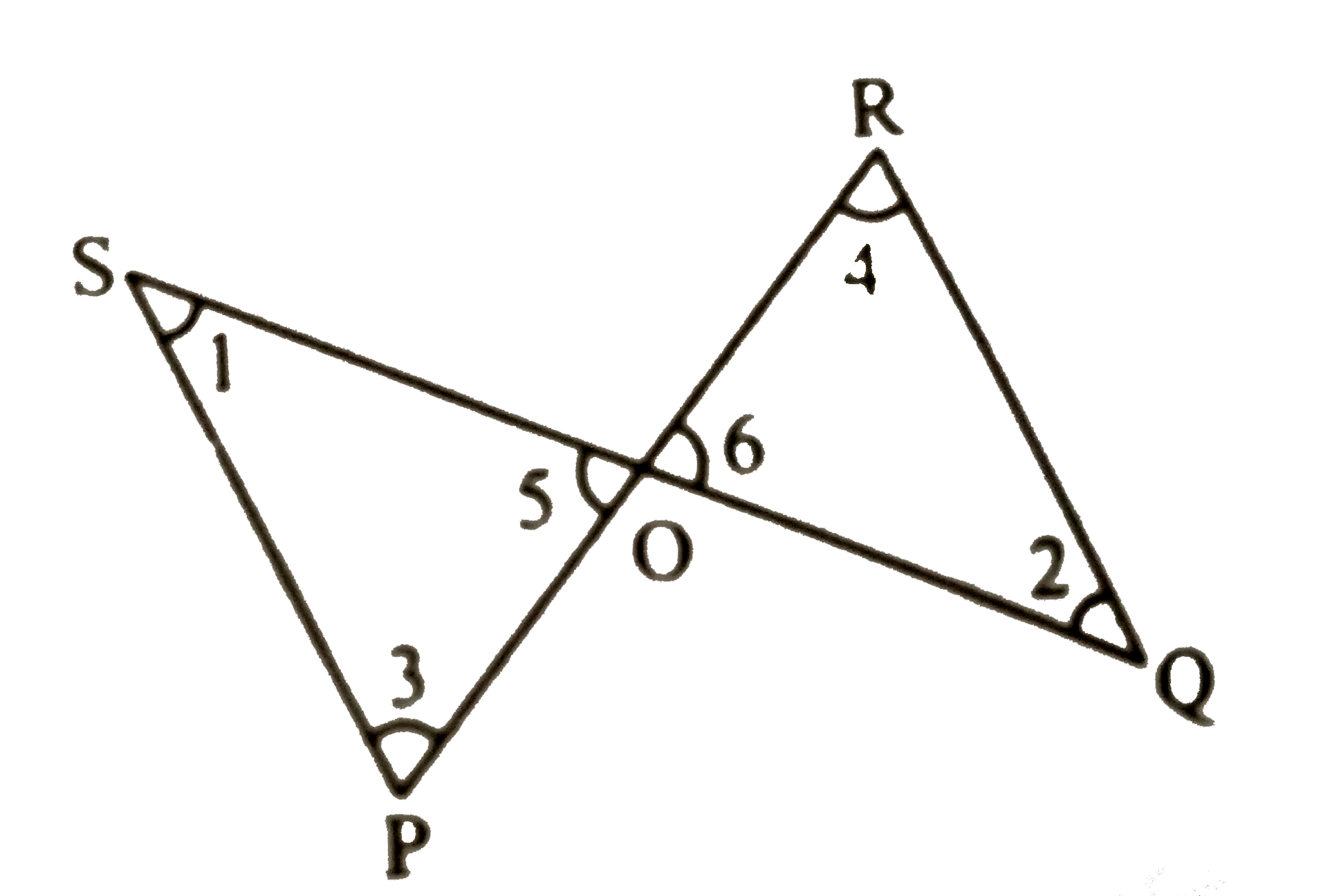
View Solutionदी गई आकृति में, `triangle POS ~ triangleROQ` है, तो सिद्ध कीजिए कि
`PS ||RQ`
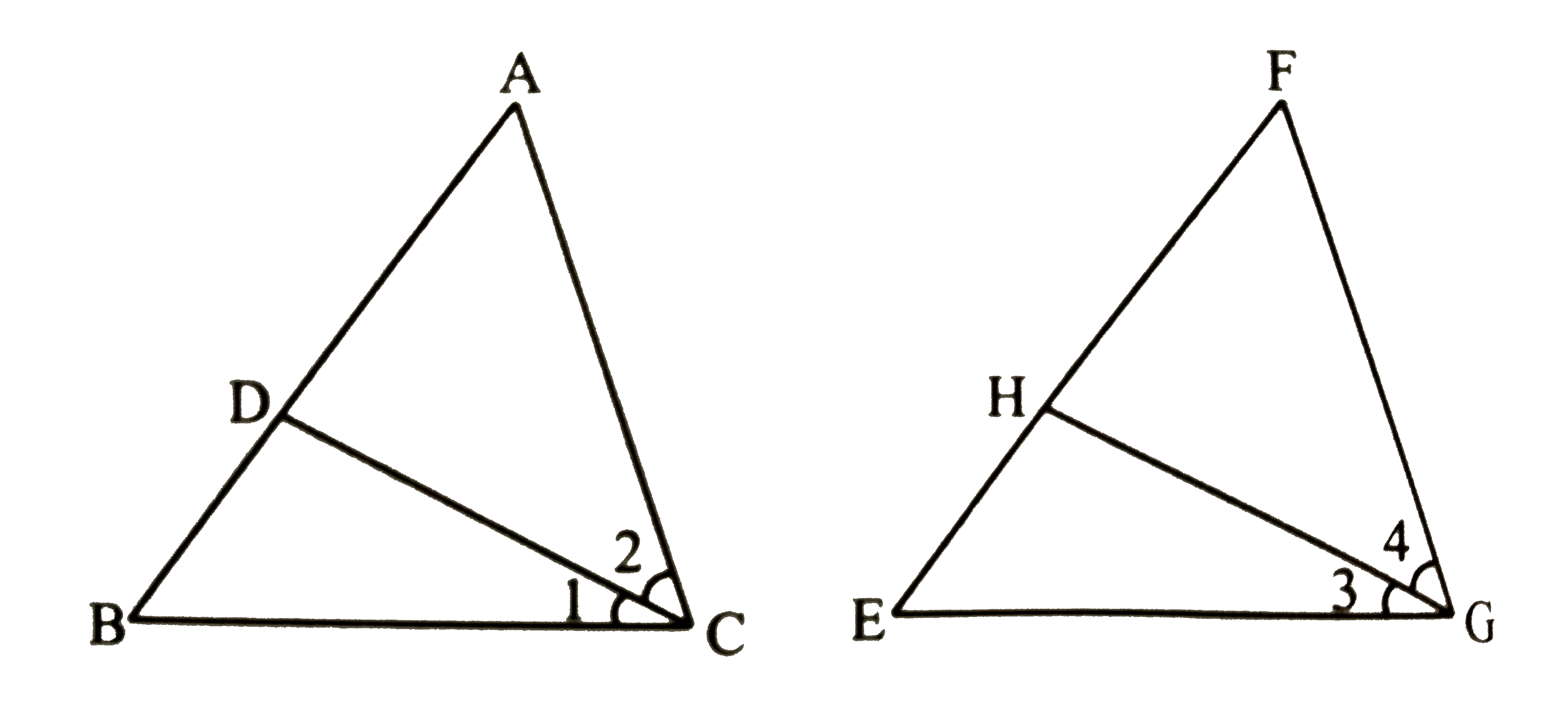
View Solutionयदि CD तथा HG (D तथा H, AB तथा FE पर है |) क्रमशः `angleACB` तथा `angleEGF` के अर्द्धक है तथा `triangle ABC ~ triangleFEG` तो सिद्ध कीजिए कि :
(i) `triangle DCA ~ triangleHGF`
(ii) `(CD)/(GH) = (AC)/(FG)`
(iii) `triangle ~ triangleHGE`
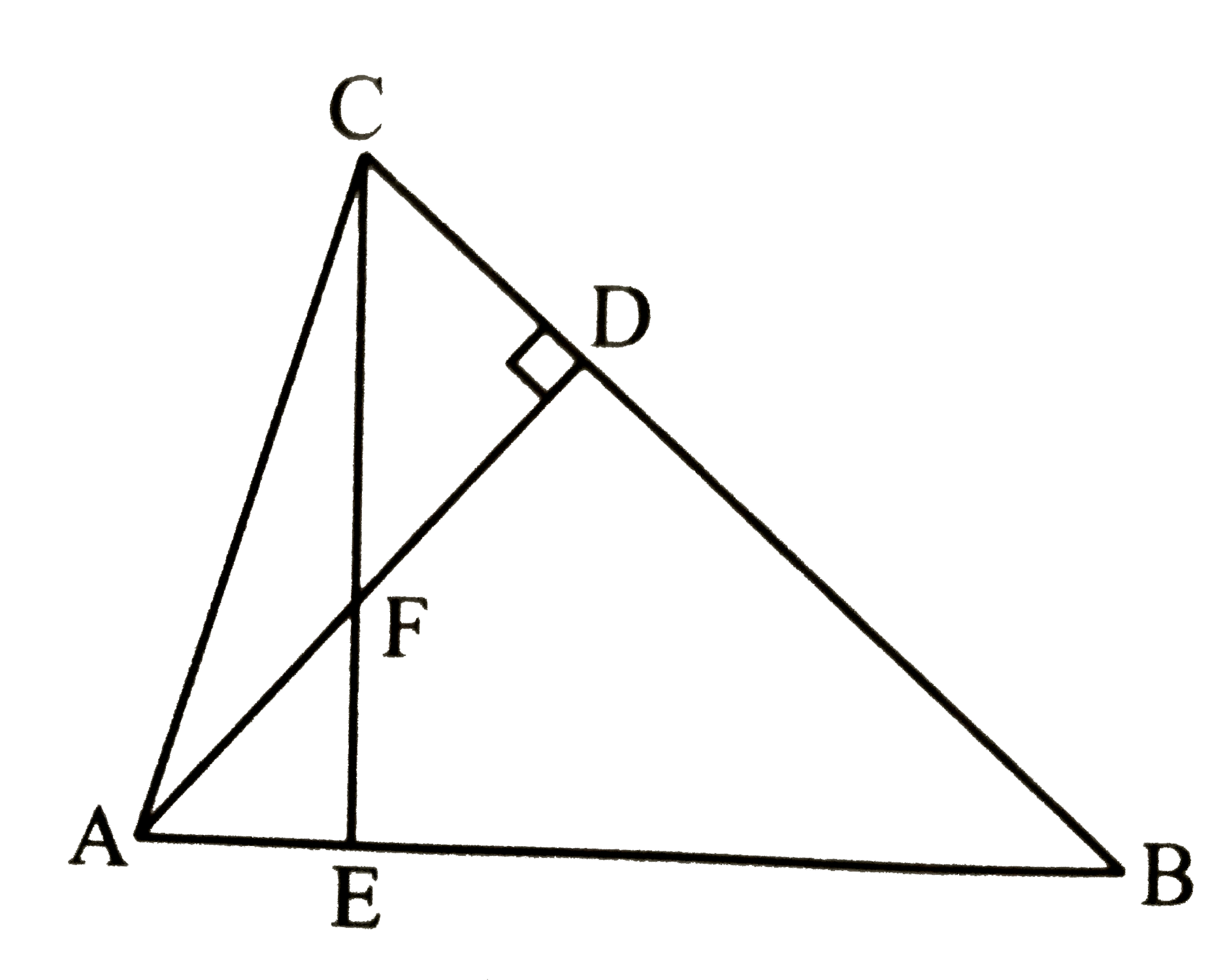
View Solutionदी गई आकृति में, `triangleABC` की दो ऊँचाइयो AD तथा CE है तो सिद्ध कीजिए कि :
`(i) triangleAEF ~ triangleCDF`
(ii) `triangleABD ~ triangleCBE`
(iii) `triangleAEF ~ triangleADB`
(iv) `triangleFDC ~ triangle BEC`
View Solutionदी गई आकृति में, यदि `BD bot AC` तथा `CE bot AB` है तो सिद्ध कीजिए :
(i) `triangleAEC ~ triangleADB`
(ii) `(CA)/(AB) = (CE)/(DB)`
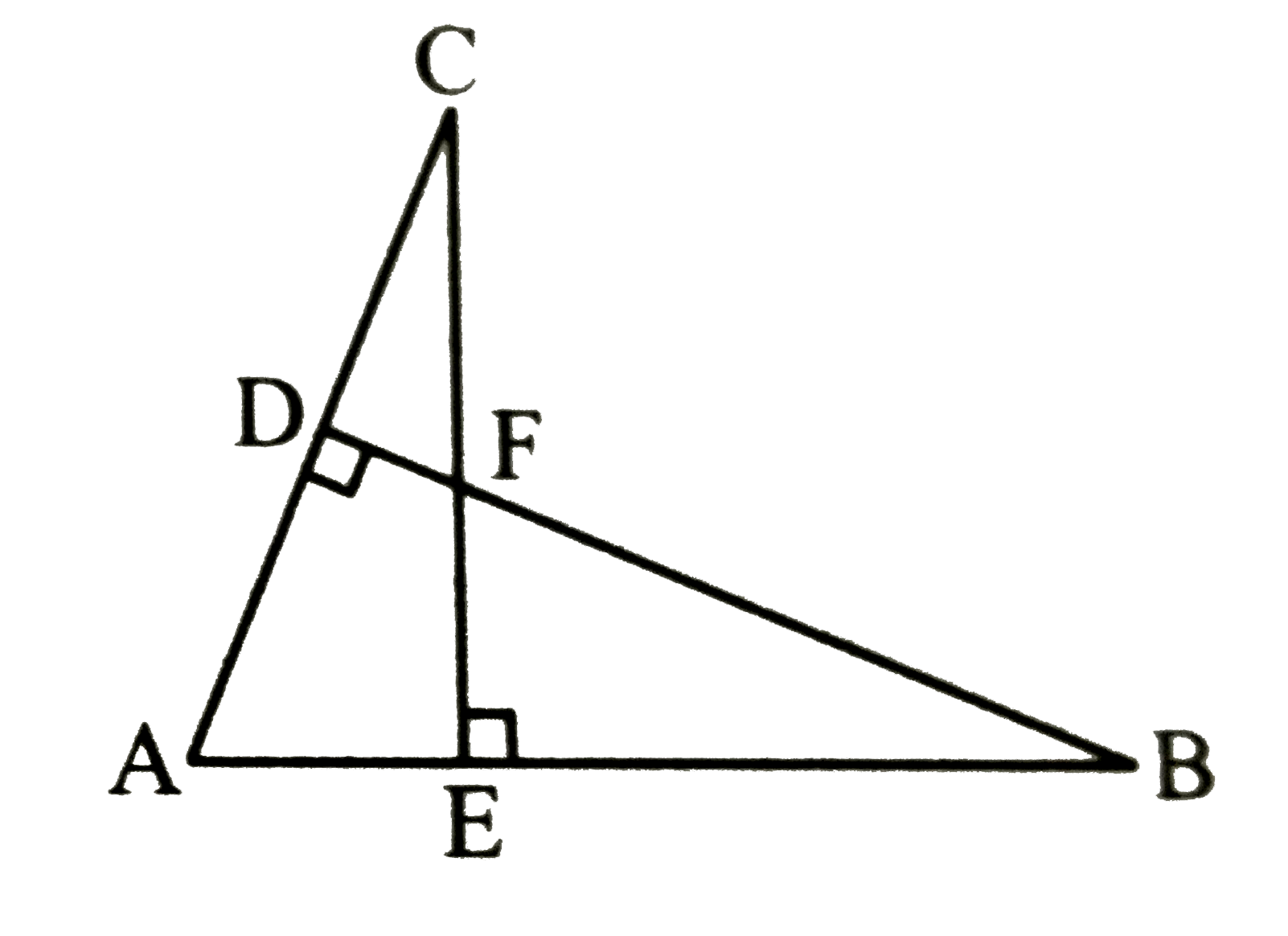
View Solutionएक `triangleABC` में, भुजा BC पर एक बिंदु D है तथा `angle ADC = angle BAC` है तो सिद्ध कीजिए कि
`(CA)/(CD) = (CB)/(CA)`
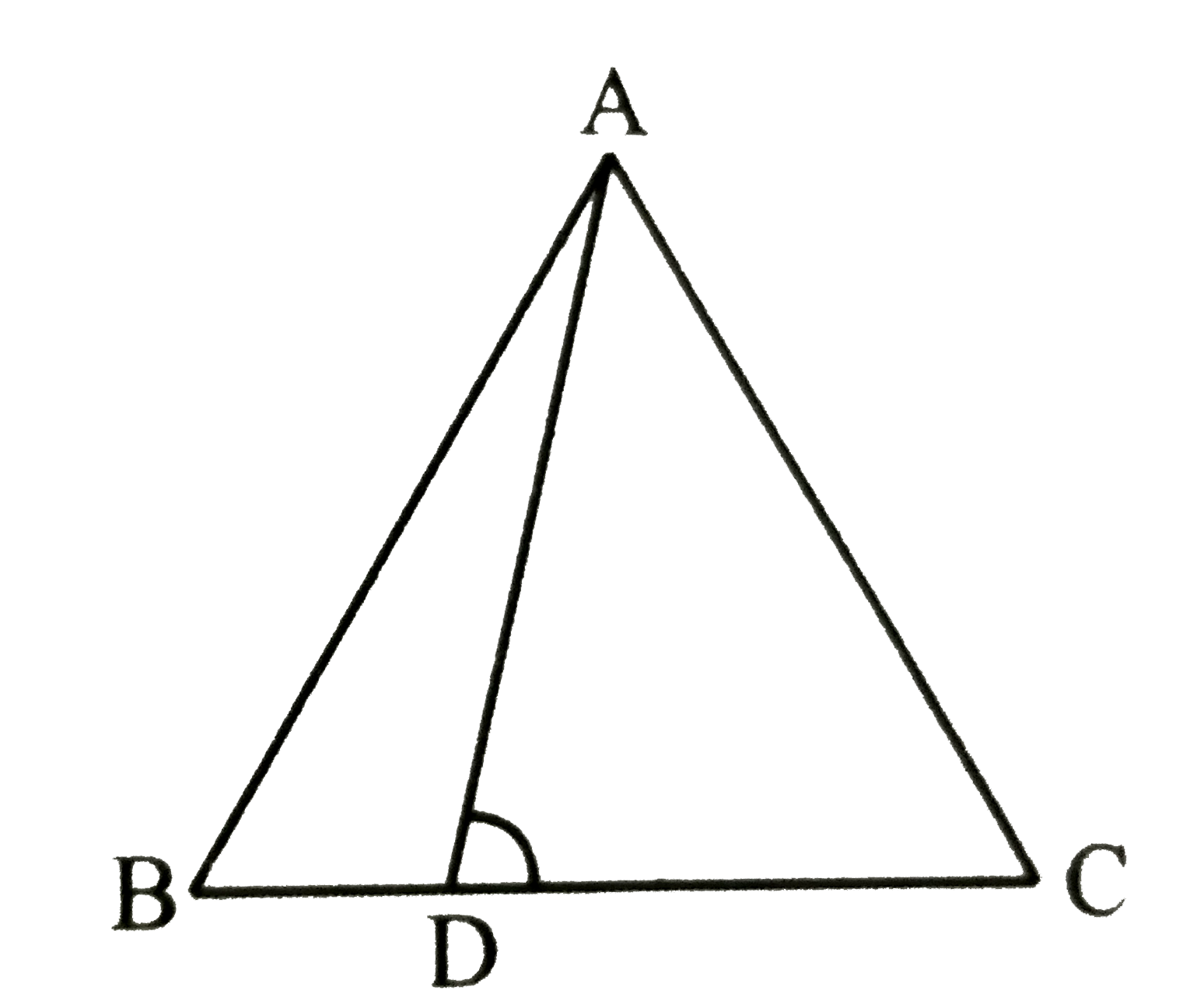
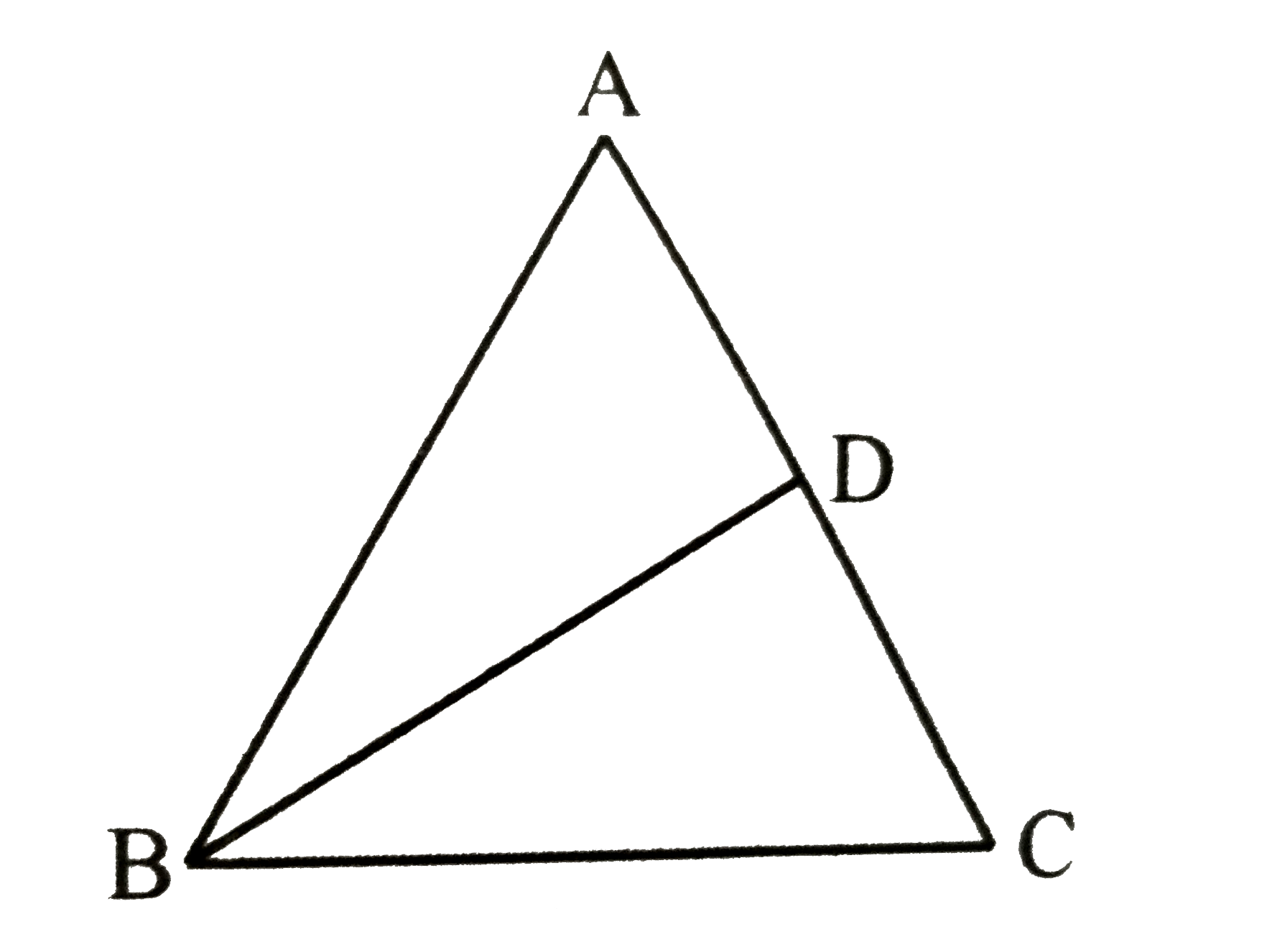
View Solutionमाना एक `triangle ABC` है जिसमे AB = AC तथा AC पर एक बिंदु D है और `BC ^(2) = AC xx CD` तो सिद्ध कीजिए कि BD = BC
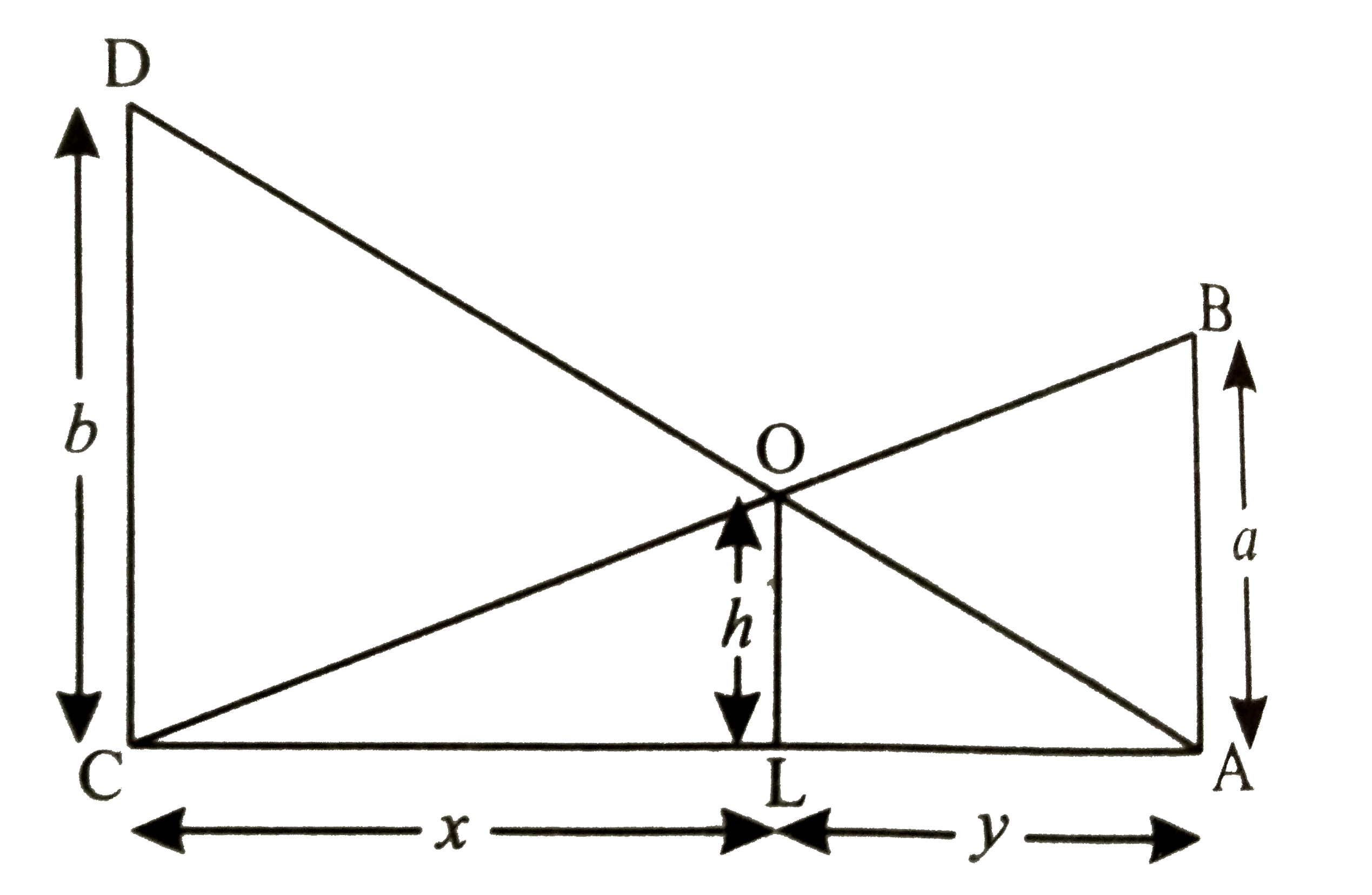
View Solutiona व b मीटर ऊँचाई के तथा p मीटर की दुरी पर स्थित दो खम्बे है | सिद्ध कीजिए कि दोनों खम्बो के शीर्षो को मिलाने वाली रेखा के प्रतिच्छेद बिंदु की ऊँचाई `(ab)/(a + b)` मीटर होगी |
View Solutionएक समांतर चतुर्भुज ABCD में भुजा AD पर कोई बिंदु E है तथा BE, CD को F पर प्रतिच्छेद करता है तो सिद्ध कीजिए कि `triangle ABE ~ triangleCFB`
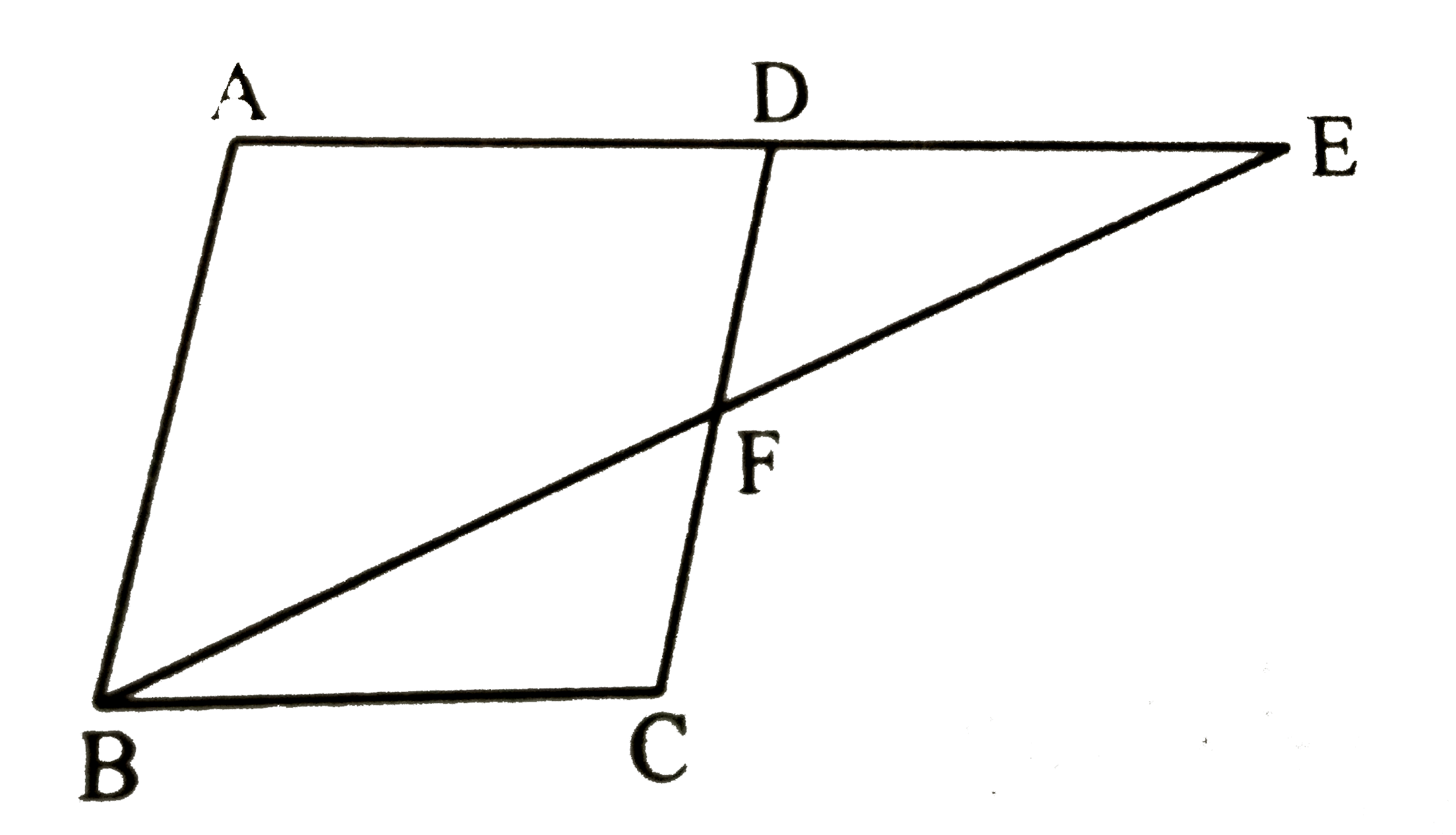
View Solutionदी गई आकृति में, एक समकोण त्रिभुज ABC है जो B पर समकोण है | तथा B से AC पर एक लम्ब है जिसका निचला भाग D है यदि `DM bot BC` तथा `DN bot AB` है तो सिद्ध कीजिए कि
`(i) (DM)^(2) = DN xx MC`
(ii) `(DN)^(2) = DM xx AN`
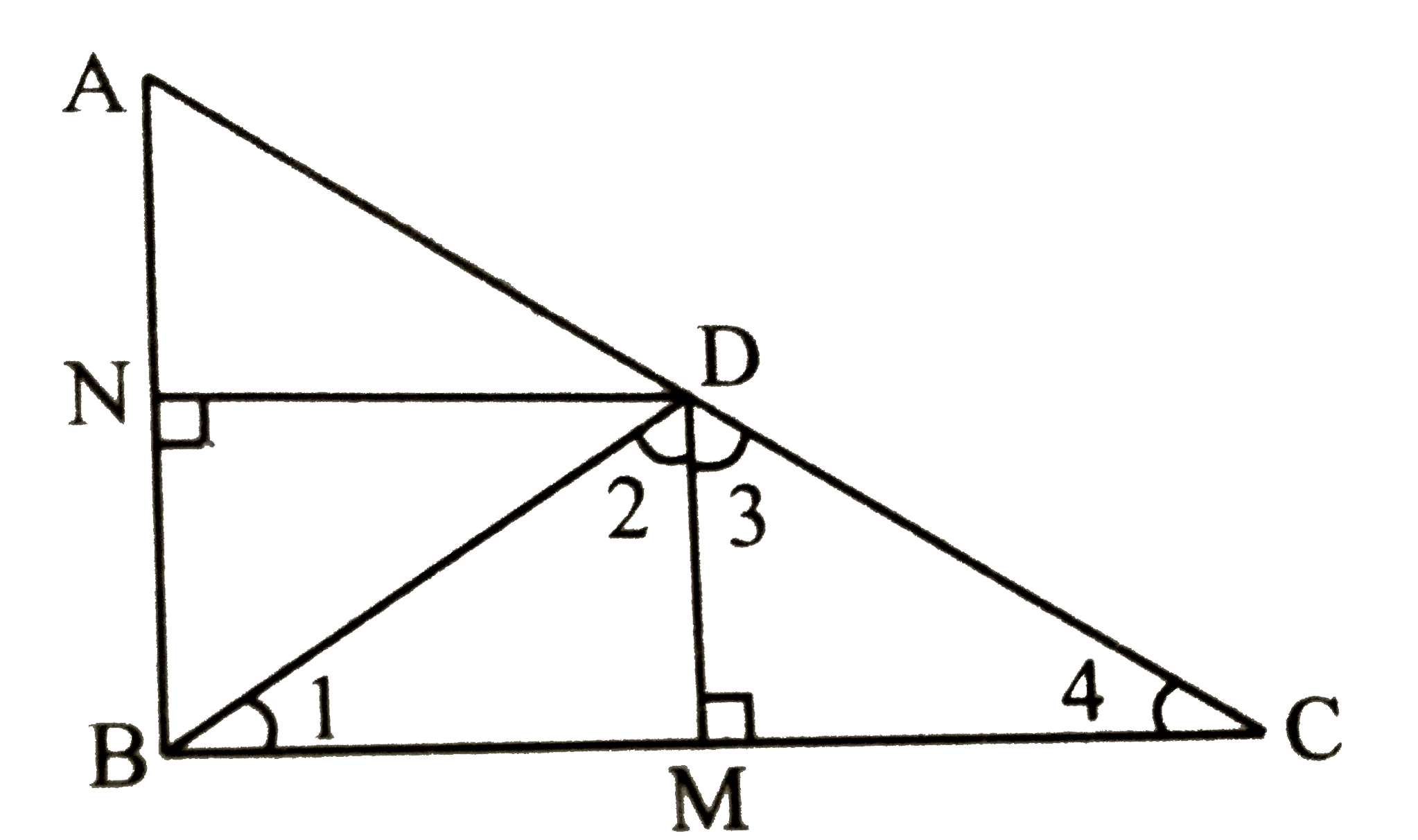
View Solutionदी गई आकृति में समद्विबाहु त्रिभुज ABC की भुजा CB के बड़े भाग पर E इस प्रकार है कि `EF bot AC` है और `AB = AC` है यदि `AD bot BC` हो तो सिद्ध कीजिए कि `triangle BD ~ triangle ECF`
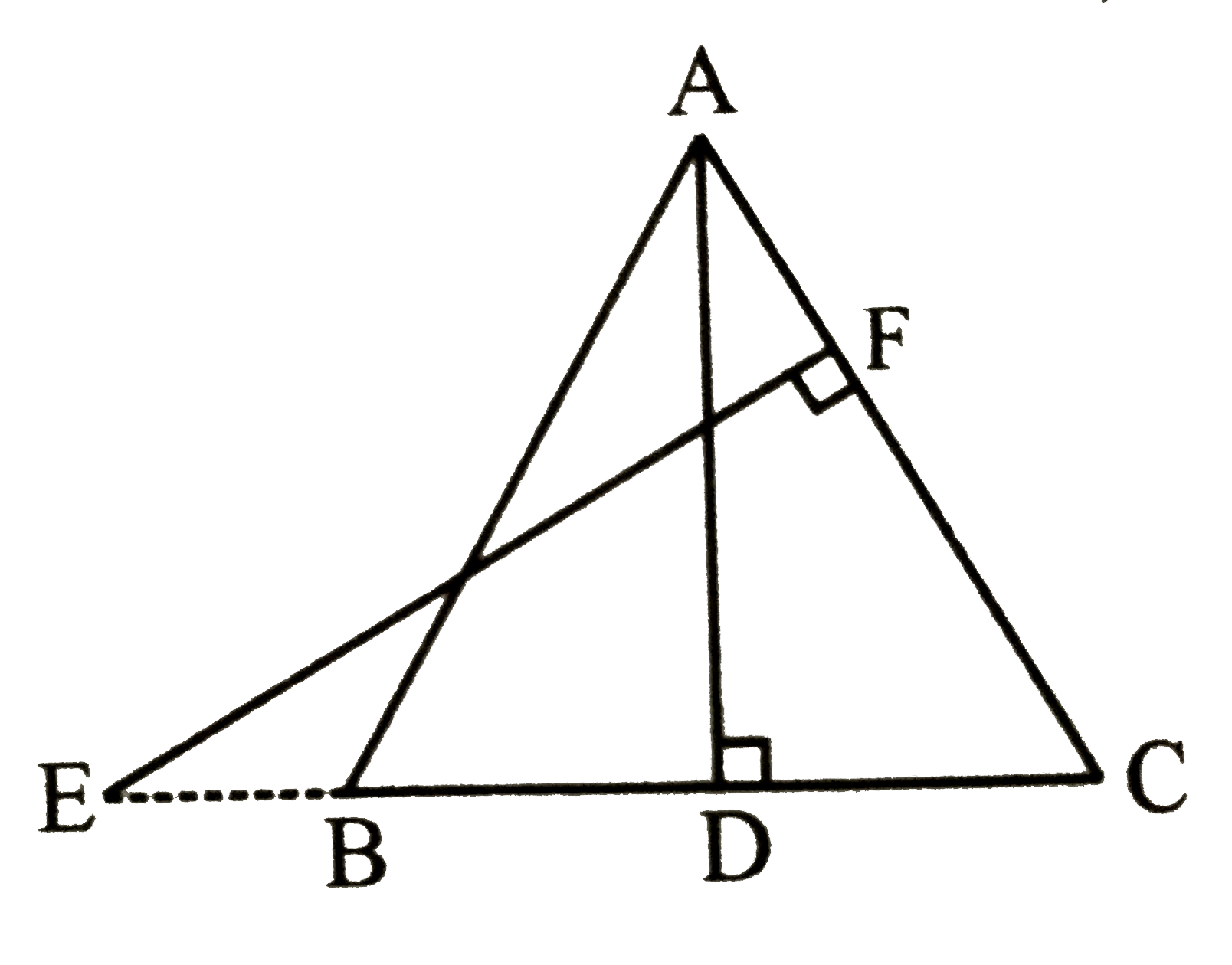
View Solutionदी गई आकृति में `(OA)/(OC) = (OD)/(OB)` है तो सिद्ध कीजिए कि `angle A = angleC` तथा `angleB = angle D`
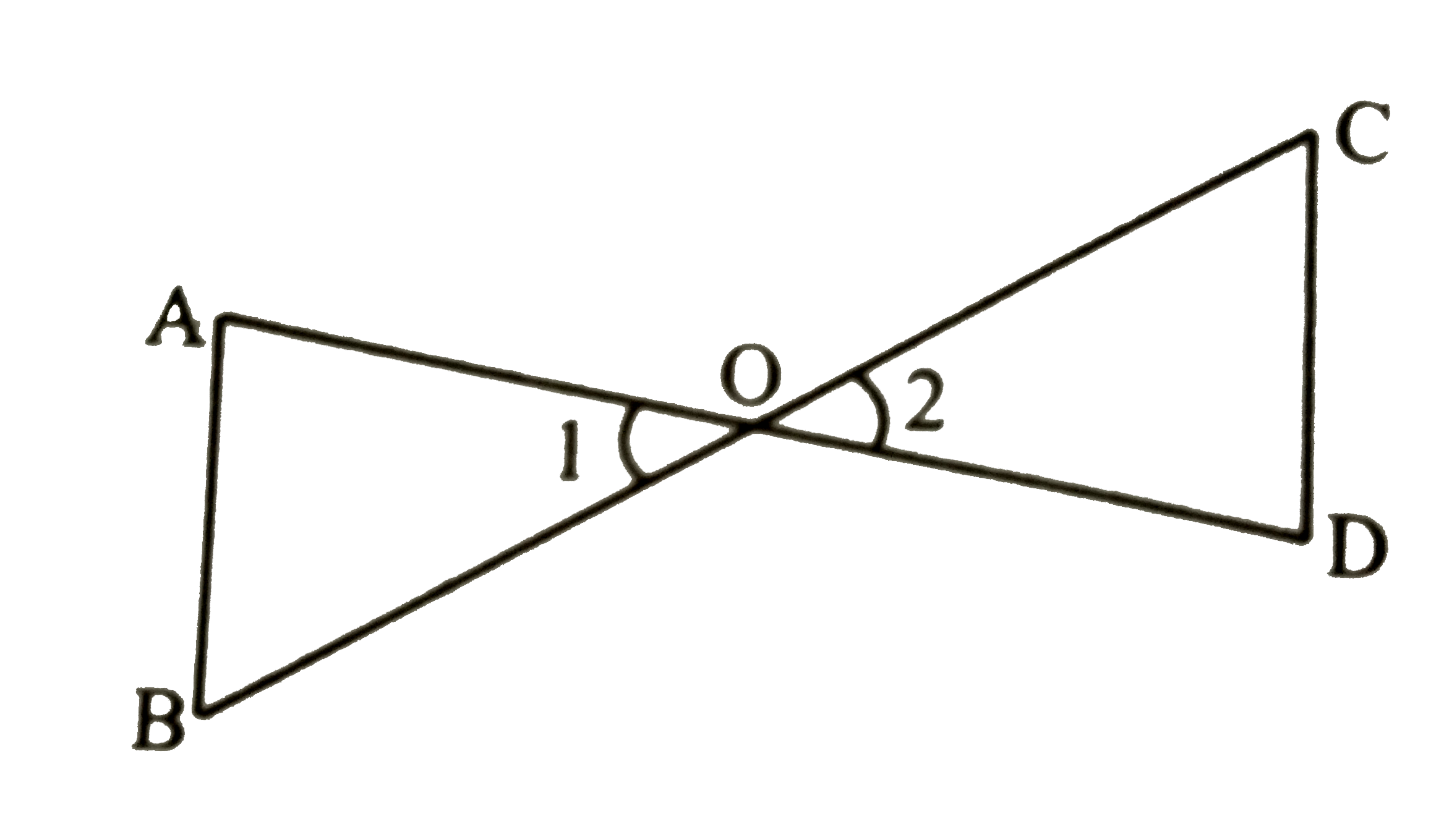
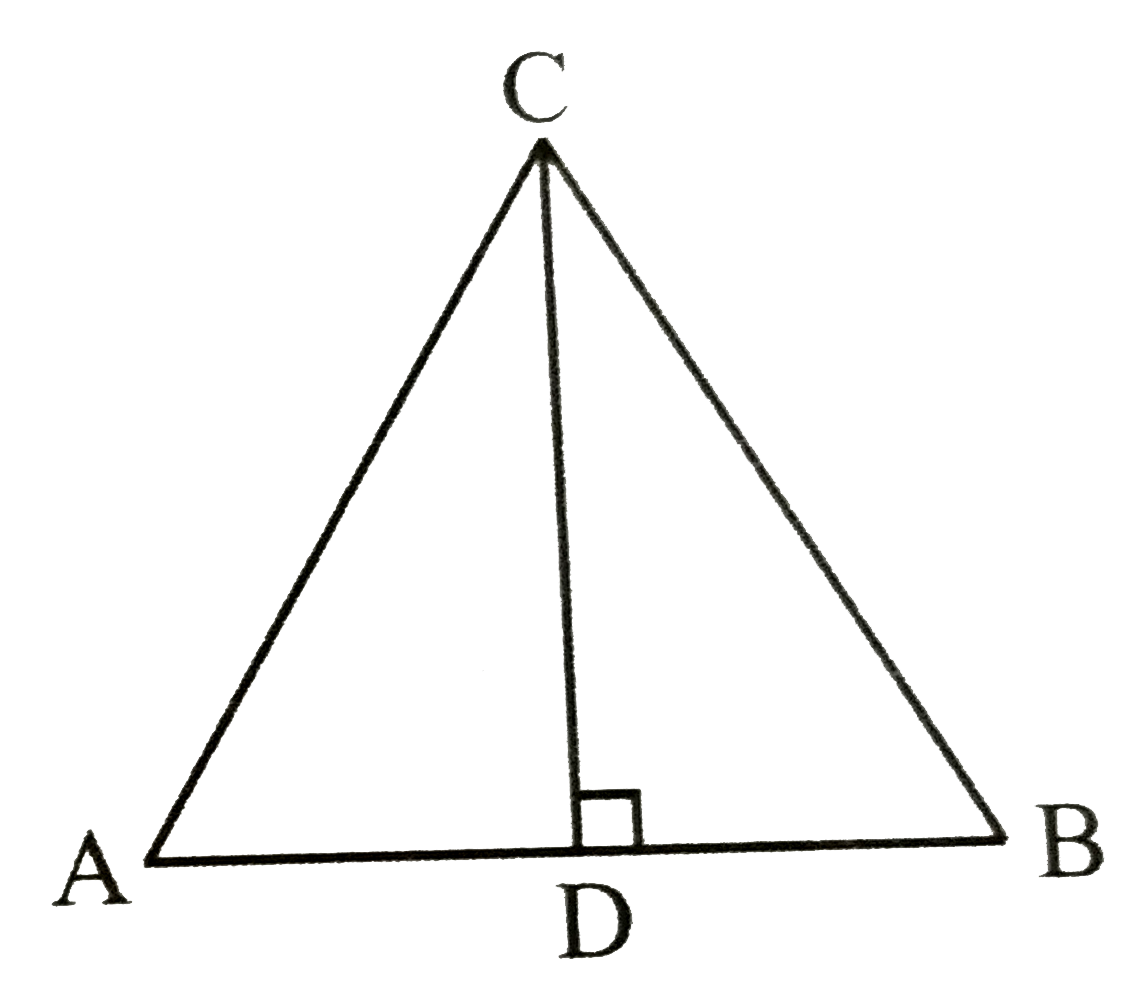
View Solutionदी गई आकृति में, `angle ACB = 90^(@)` तथा `CD bot AB` है तो सिद्ध कीजिए कि
`(CB^(2))/(CA^(2)) = (BD)/(AD)`
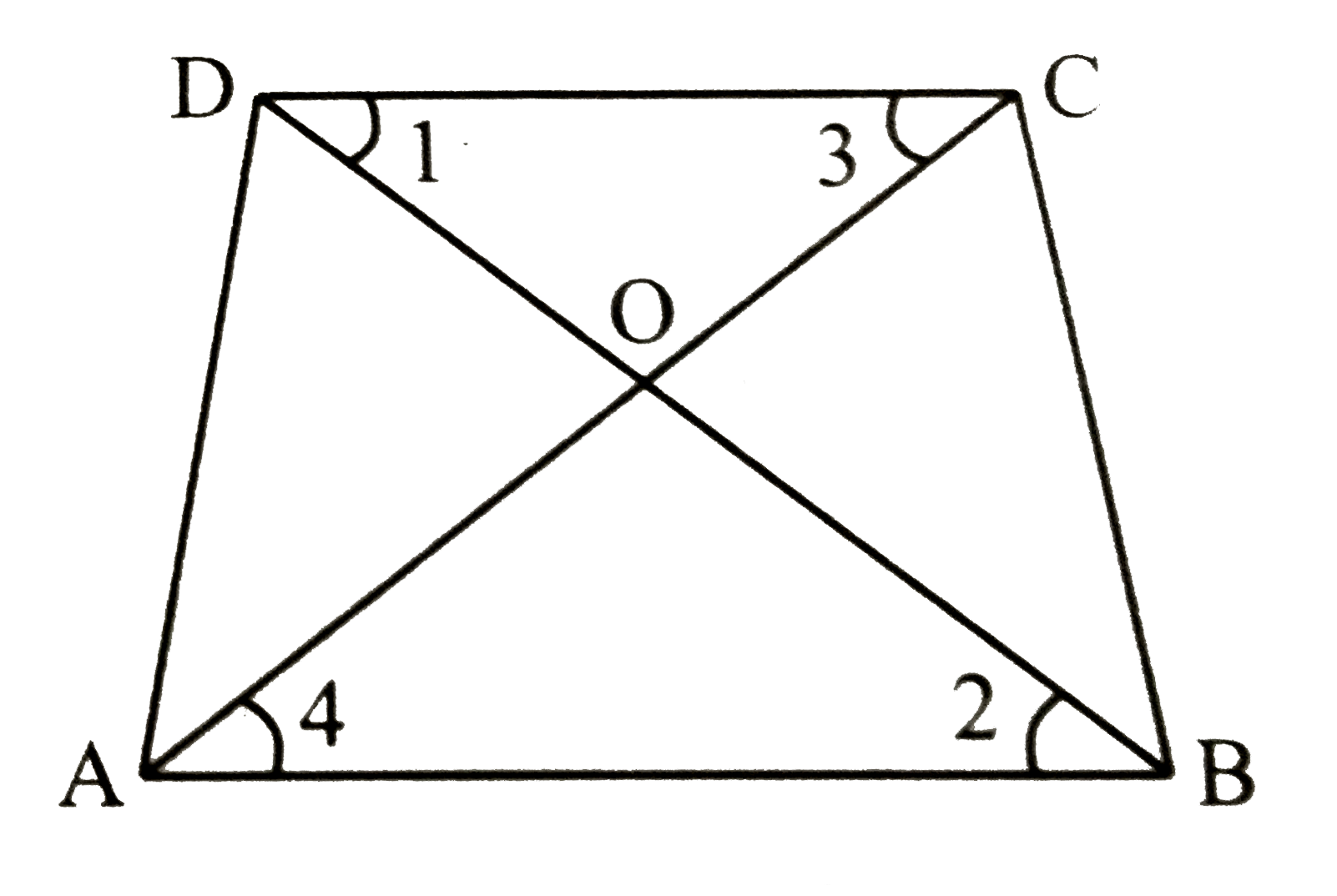
View SolutionABCD एक समलम्ब चतुर्भुज है जिसमे `AB ||DC` विकर्ण AC और BD एक-दूसरे को O बिंदु पर प्रतिच्छेद करते है दो त्रिभुजों के लिए समरूपता का प्रयोग करते हुए दर्शाइये कि `(OA)/(OC) = (OB)/(OD)`
View Solution6 मीटर ऊँचा एक ऊर्ध्वाधर स्तम्भ जमीन पर 4 मीटर लम्बी छाया बनाता है और ठीक उसी मीनार 28 मीटर लम्बी छाया बनाता है | मीनार की ऊँचाई ज्ञात कीजिए
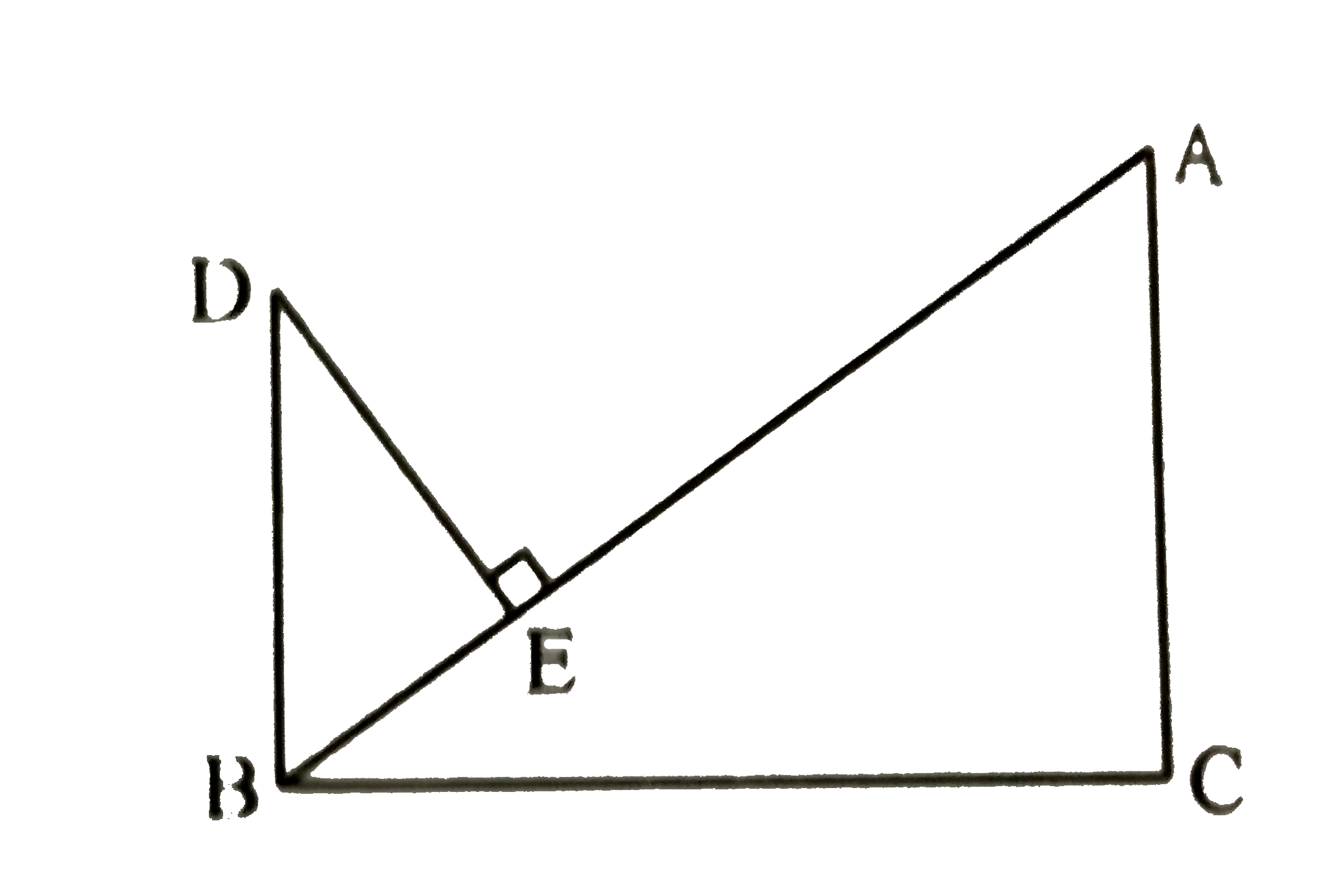
View Solutionदी गई आकृति में, `DB bot BC, DE bot AB, AC bot BC` है तो सिद्ध कीजिए कि `(BE)/(DE) = (AC)/(BC)`
View Solutionदो समरूप त्रिभुजों का परिमाप क्रमशः 25 सेमी० तथा 15 सेमी० है | यदि पहले त्रिभुज की एक भुजा 9 सेमी० है तो उसके संगत दूसरे त्रिभुज की भुजा ज्ञात कीजिए |
View Solutionयदि AD तथा PM क्रमशः `triangle ABC` तथा `triangle PQR` के समद्विभाजक है जहाँ `triangle ABC ~ triangle PQR` है तो सिद्ध कीजिए कि :
(i) `(AB)/(PQ) = (AD)/(PM)`
(ii) ` angle ADC = angle PMR `
View Solutionएक `triangle ABC` की क्रमशः भुजाएँ AB और BC तथा मध्यम AD है | जो `triangle PQR` की भुजाओं और तथा मध्यम PM के समानुपाती है | तो सिद्ध कीजिए कि `triangle ABC ~ triangle PQR`
View Solution`triangle PQR` की भुजा PR तथा QR पर बिंदु S तथा T है तथा `angle P = angle RTS` तो दिखाइये कि, `triangle RPQ ~ RTS`
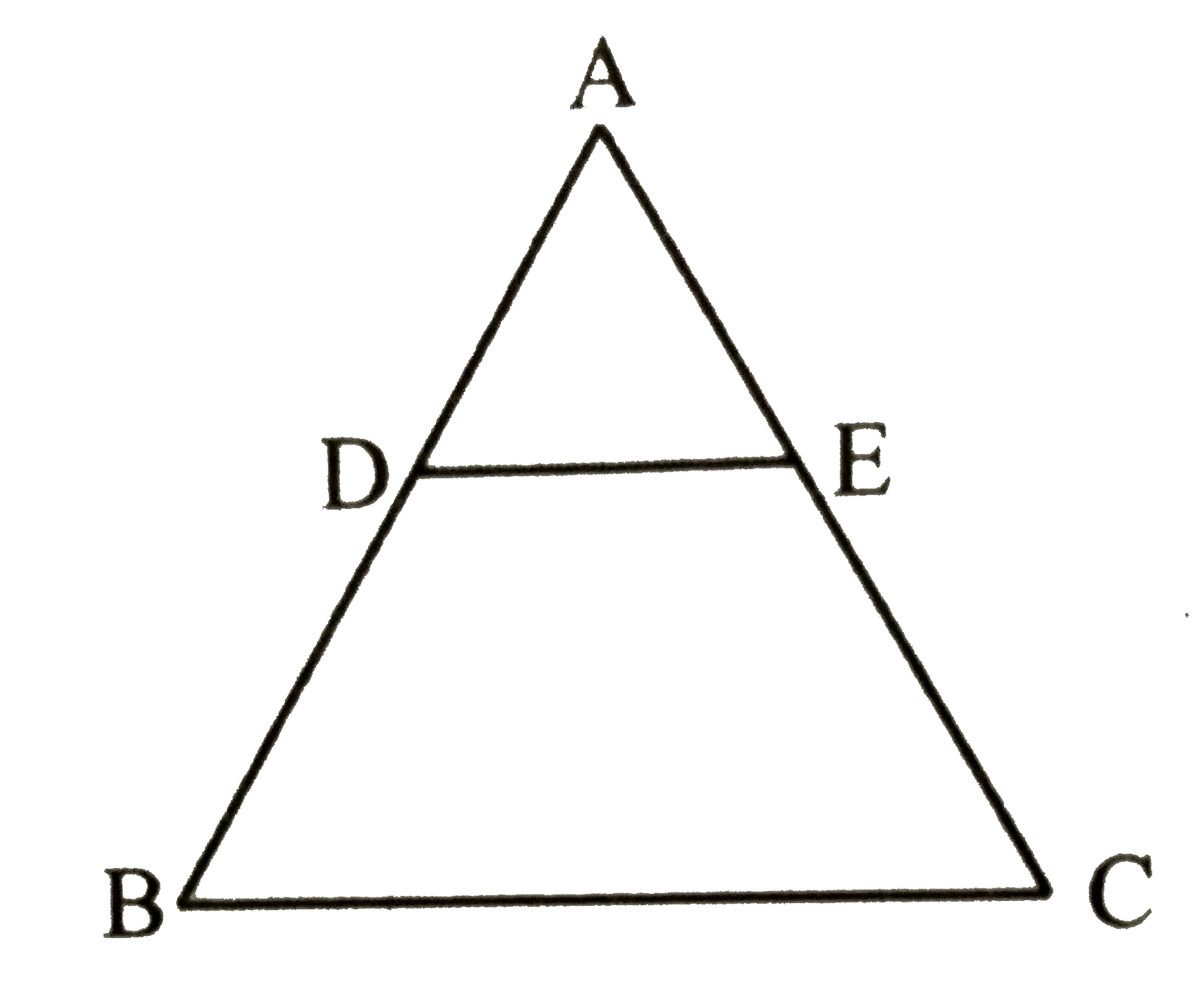
View Solutionदी गई आकृति में, `DE ||BC, AD = 2` सेमी०, `BD = 2.5` सेमी०, `AE = 3.2` सेमी०. `DE = 4` सेमी० है तो AC तथा BC ज्ञात कीजिए |
View Solutionदी गई आकृति में, `triangle ABC` तथा `triangle AMP` क्रमशः Bतथा M पर समकोण है तो सिद्ध कीजिए कि,
(i) `triangle ABC ~ triangle AMP`
(ii) `(CA)/(PA) = (BC)/(MP)`
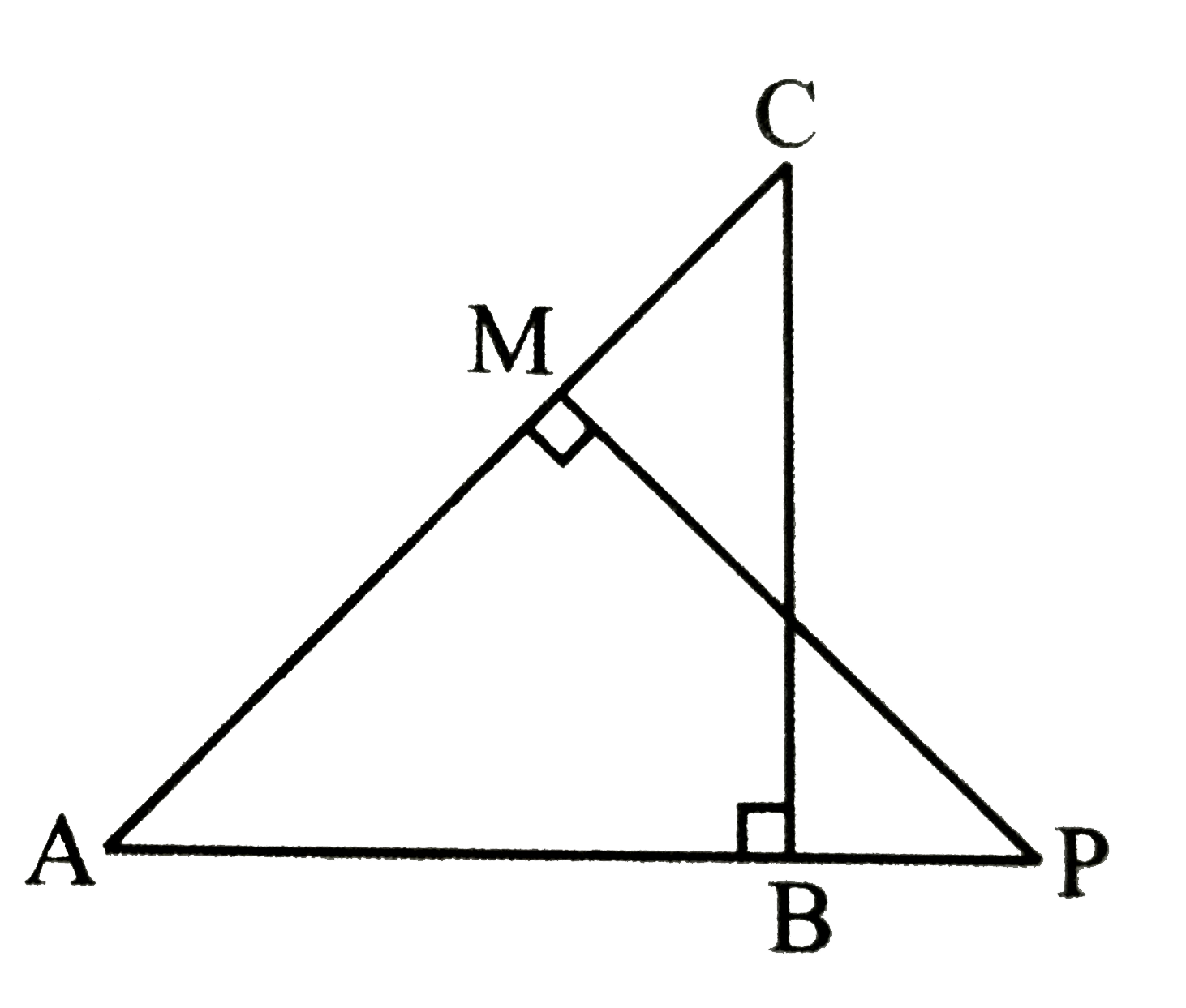
View Solution`triangle ABC` में, DE आधार BC के समान्तर है | D तथा E क्रमशः AB तथा ACपर है यदि `(AD)/(DB) = (2)/(3)` है तो `(BC)/(DE)` ज्ञात कीजिए |
View Solutionदी गई आकृति में, `triangle PQR ~ triangle XYZ` यदि `PQ = 4` सेमी०, `QR = 5` सेमी० तथा XY = 6 सेमी० है तो YZ ज्ञात कीजिए |
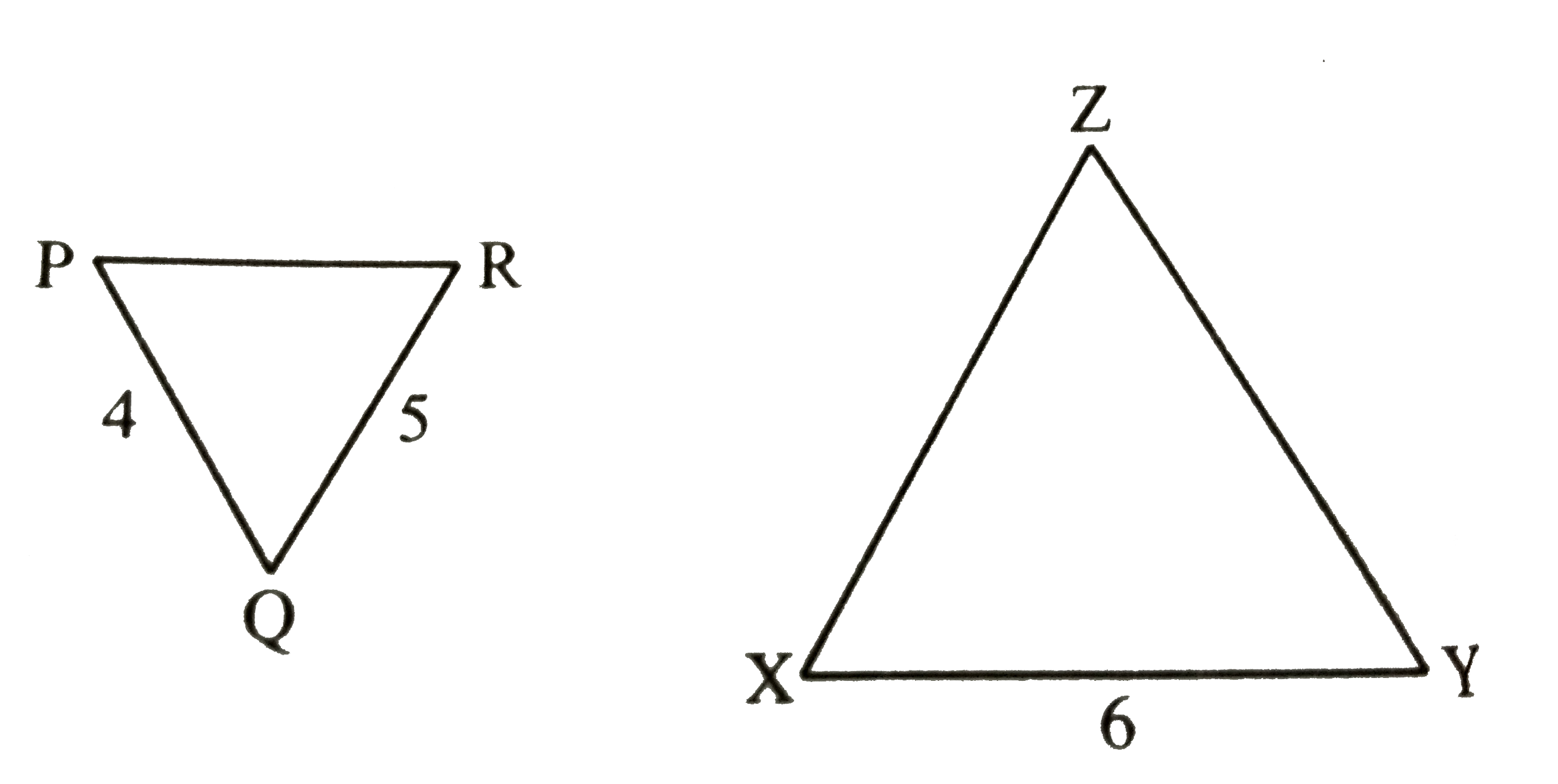
View Solution`triangle ABC` में `angleA` अधिक कोण है, `BP bot AC` तथा `QC bot AB` है तो सिद्ध कीजिए कि `AB xx AQ = AC xx AP`
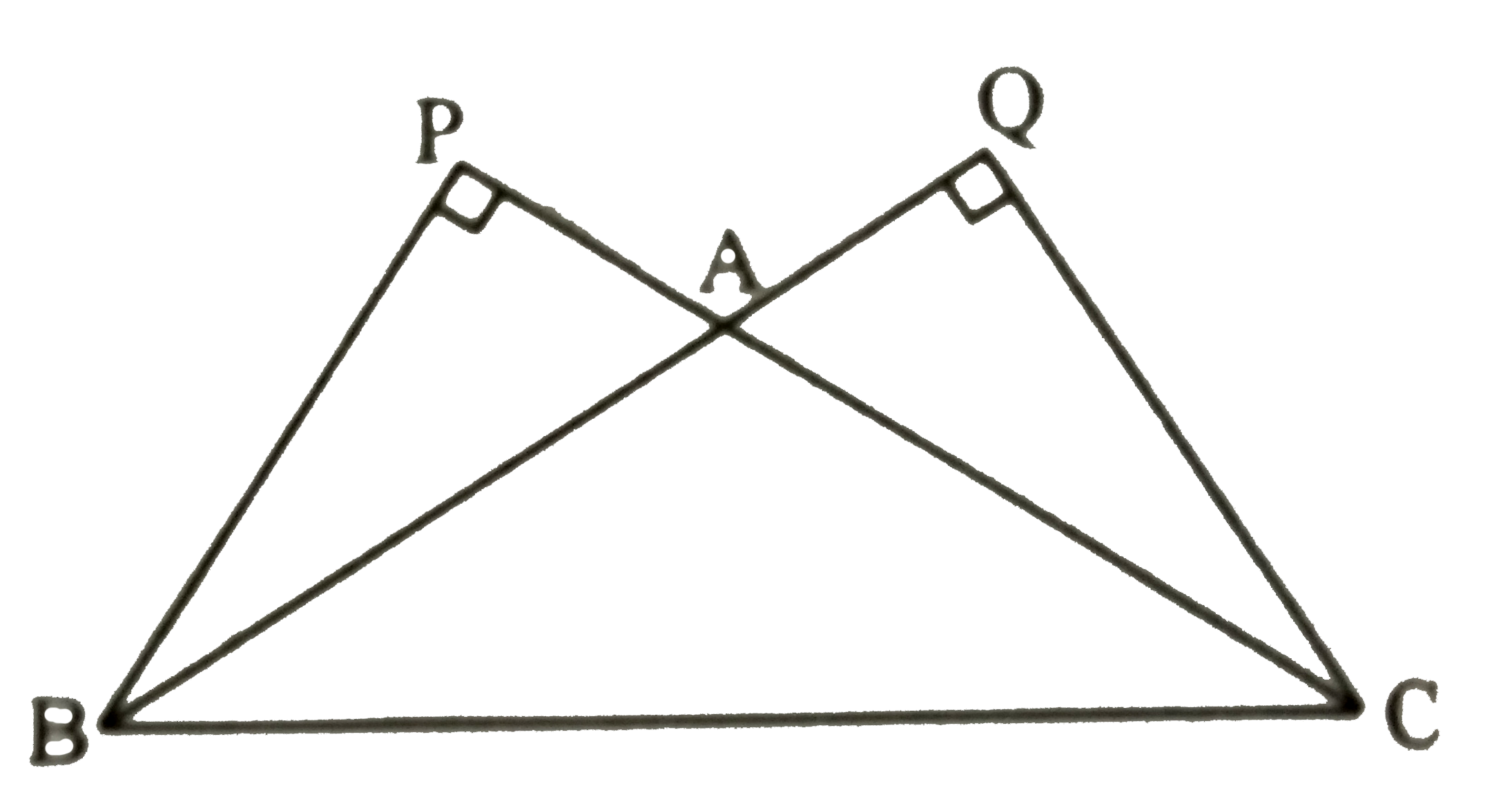
View Solutionदी गई आकृति में, एक वर्ग DEFG है तथा `angle BAC = 90^(@)` है तो सिद्ध कीजिए कि
(i) `triangleAFG ~ triangle DBG`
(ii) `triangle AGF~ triangle EFC`
(iii) `triangle DBG~triangleEFC`
(iv) `(DE)^(2) = BD xx EC`
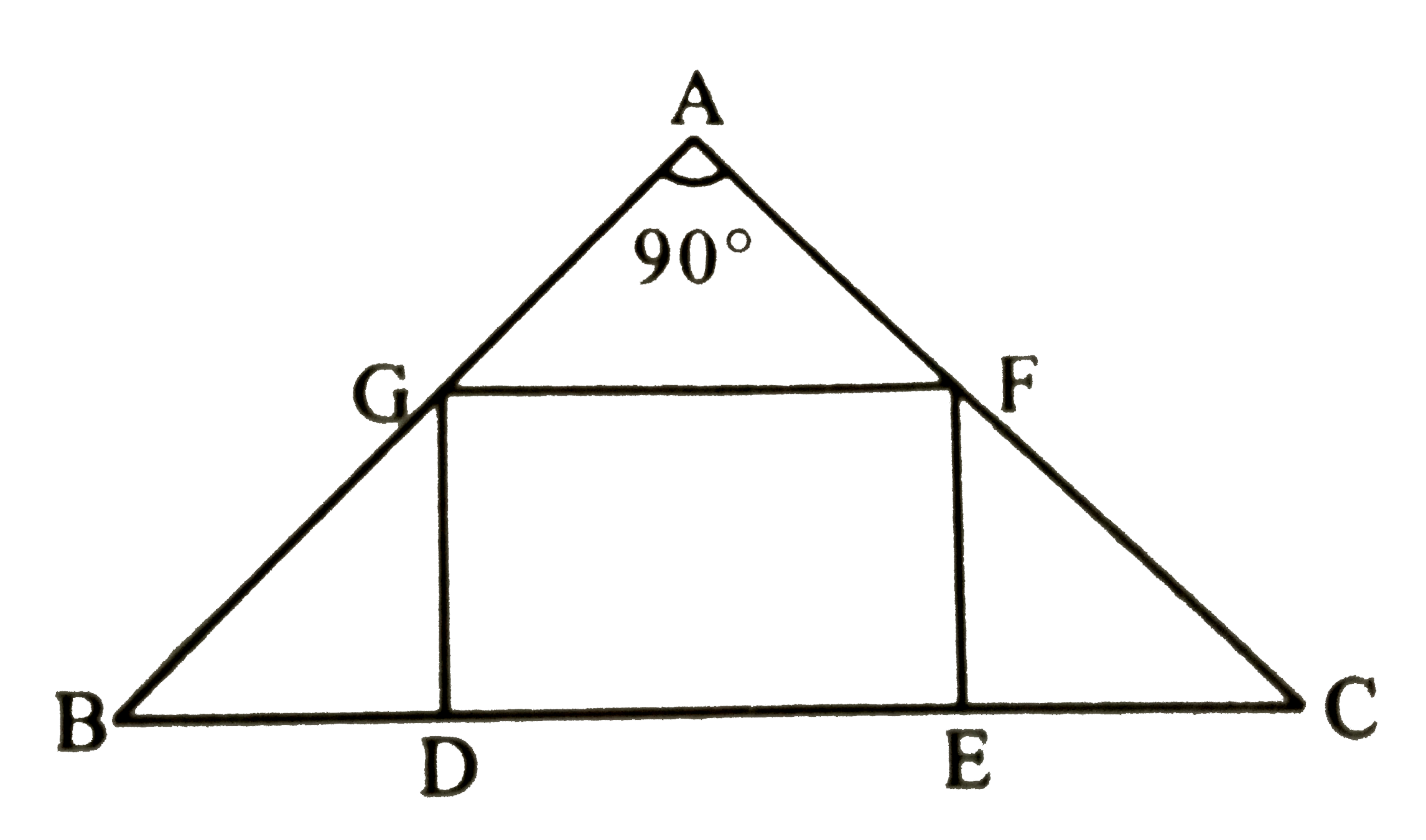
View Solutionदो समरूप त्रिभुजों ABC तथा PQR में, यदि उनकी सगत ऊँचाइयो का अनुपात `4:9` है तो `triangle ABC` तथा `triangle PQR` के क्षेत्रफलो का अनुपात ज्ञात कीजिए |
View Solutionदो समरूप त्रिभुजों ABC तथा DEF के क्षेत्रफल क्रमशः 64 सेमी`""^(2)` और 121 सेमी`""^(2)` है | यदि EF = 15.4 सेमी है तो BC का मान ज्ञात कीजिए |
View Solutionदो समरूप त्रिभुजों ABC और PQR के क्षेत्रफलो का अनुपात 9 : 16 है | यदि BC = 4.5 सेमी है तो QR की लम्बाई ज्ञात कीजिए |
View Solutionसिद्ध कीजिए कि एक वर्ग की भुजा पर बने समबाहु त्रिभुज का क्षेत्रफल उस वर्ग की विकर्ण पर बने वर्ग के क्षेत्रफल से आधा होता है |
View Solutionदी गई आकृति में, ABCD एक समलम्ब चतुर्भुज है जिसमे `AB||DC` तथा `AB = 2DC` है तो `triangle AOB` तथा `triangleCOD` के क्षेत्रफल का अनुपात ज्ञात कीजिए |
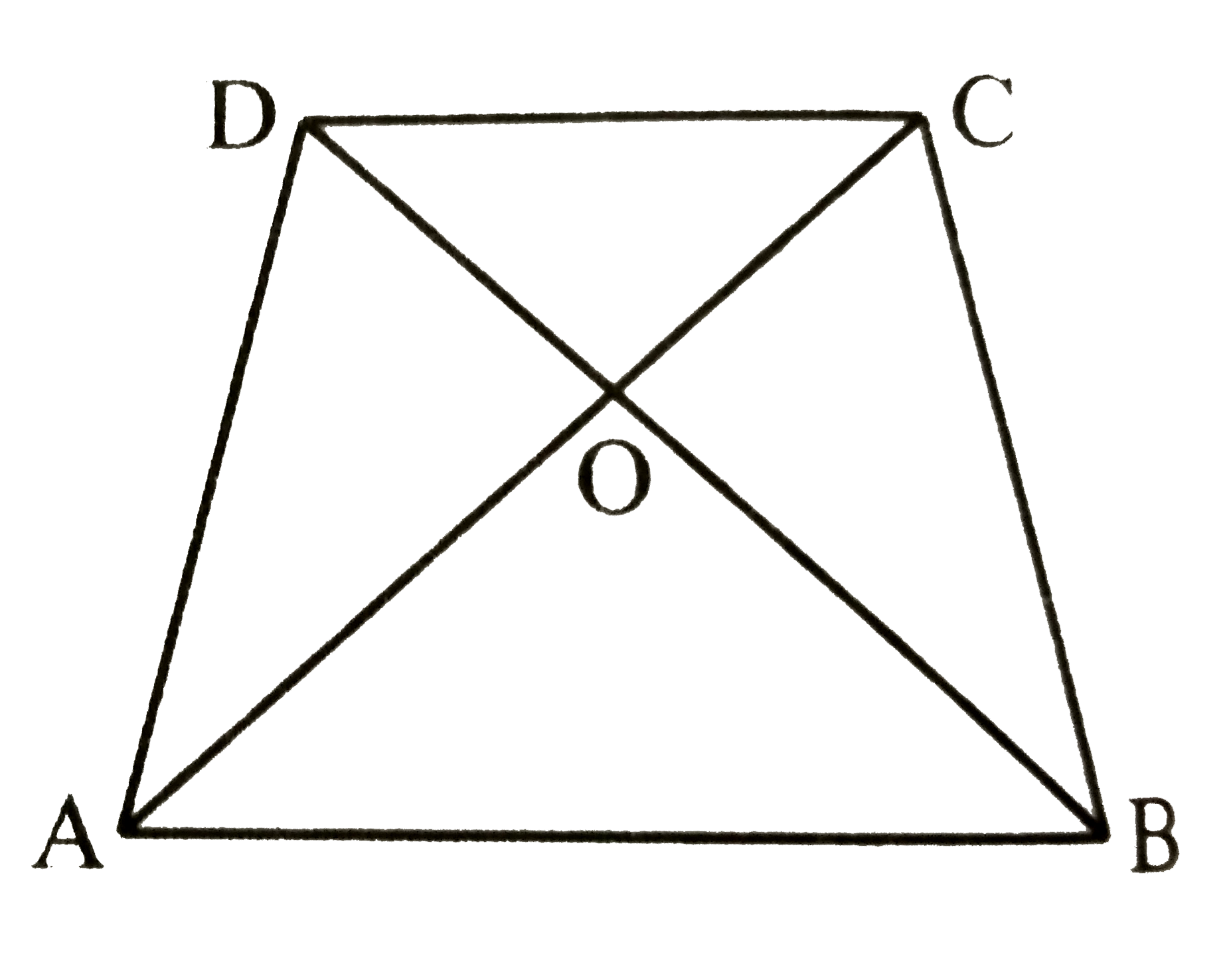
View Solutionमाना दो समरूप त्रिभुज ABC तथा DEF है तथा BC = 4 सेमी, EF = 5 सेमी और `triangle ABC` का क्षेत्रफल = 64 सेमी`""^(2)` है, तो `triangle DEF` का क्षेत्रफल ज्ञात कीजिए |
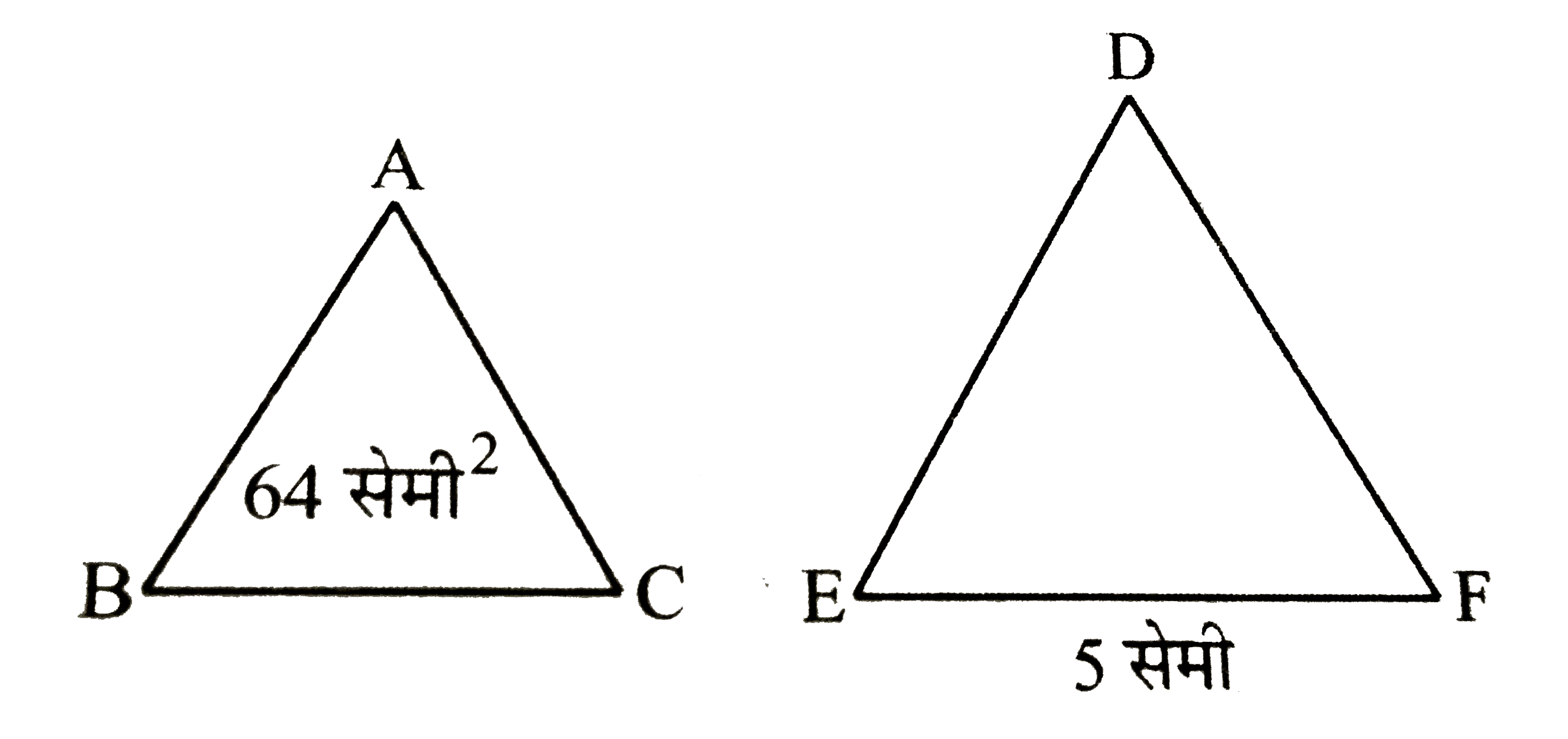
View Solutionसमलम्ब चतुर्भुज ABCD में, `AB||CD` तथा AB = 2CD है | यदि `triangle AOB` का क्षेत्रफल = 84 सेमी`""^(2)` है | तो `triangle COD` का क्षेत्रफल ज्ञात कीजिए |
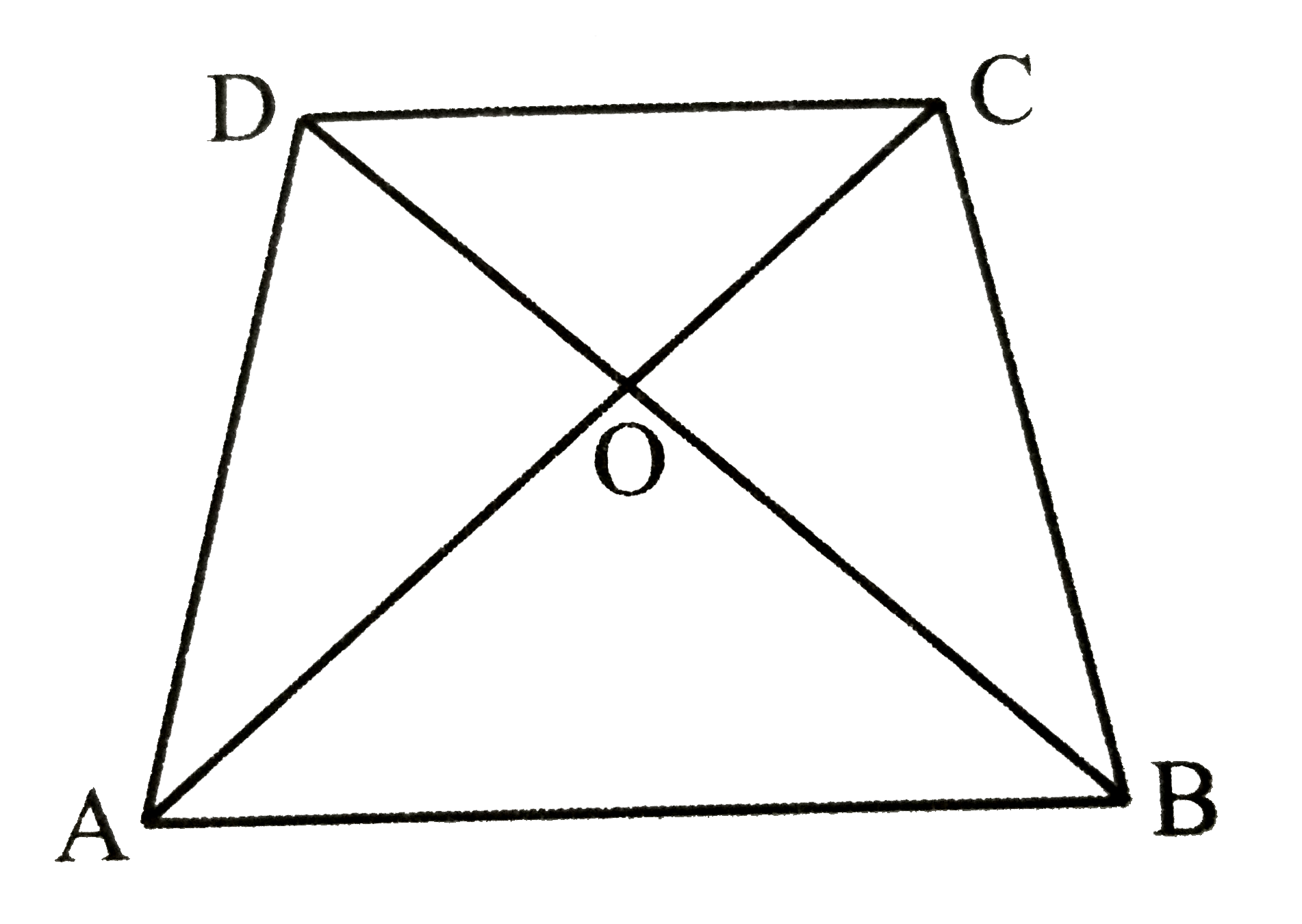
View Solutionदो समरूप त्रिभुजों के क्षेत्रफल क्रमशः 81 सेमी`""^(2)` तथा 49 सेमी`""^(2)` है | यदि बड़े त्रिभुज की ऊँचाई 4.5 सेमी है | तो छोटे त्रिभुज की संगत ऊँचाई ज्ञात कीजिए |
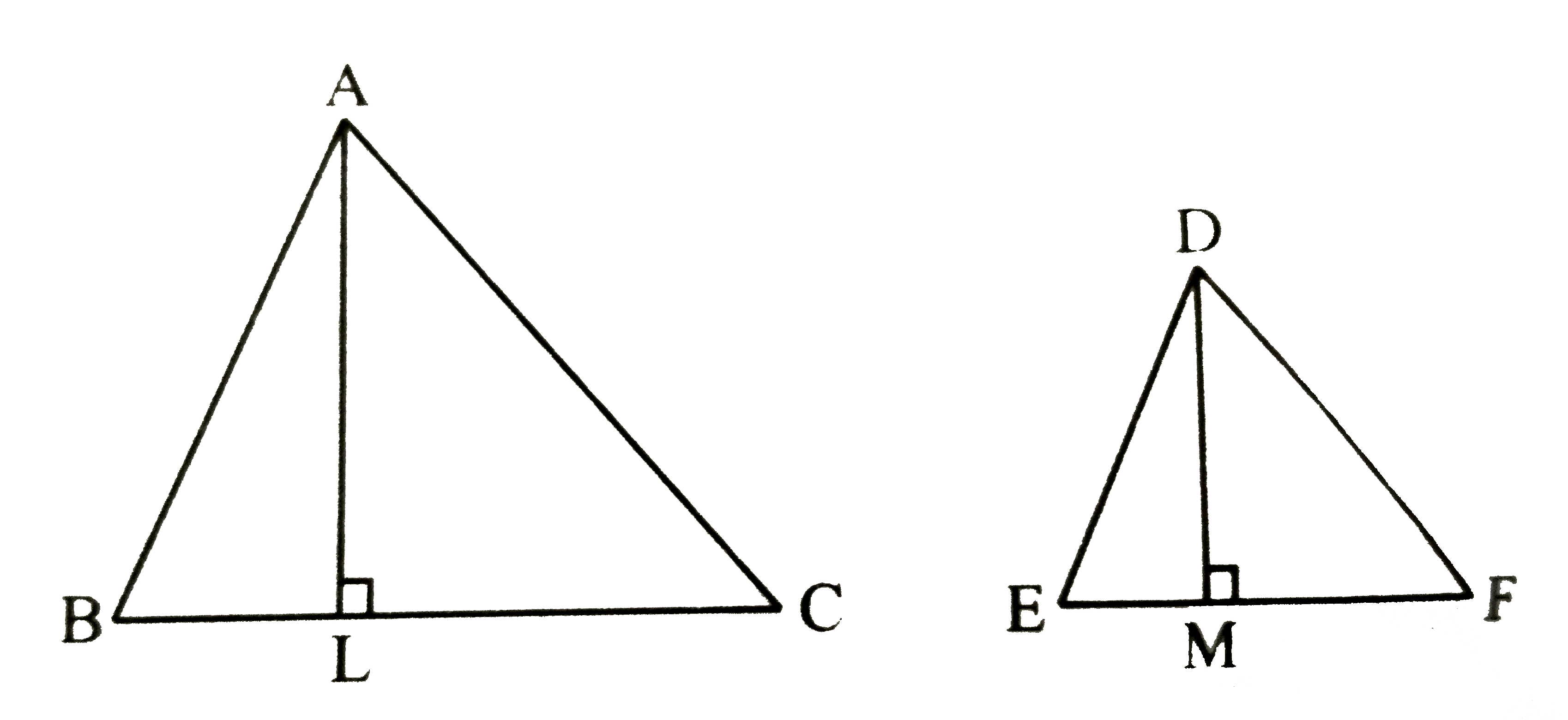
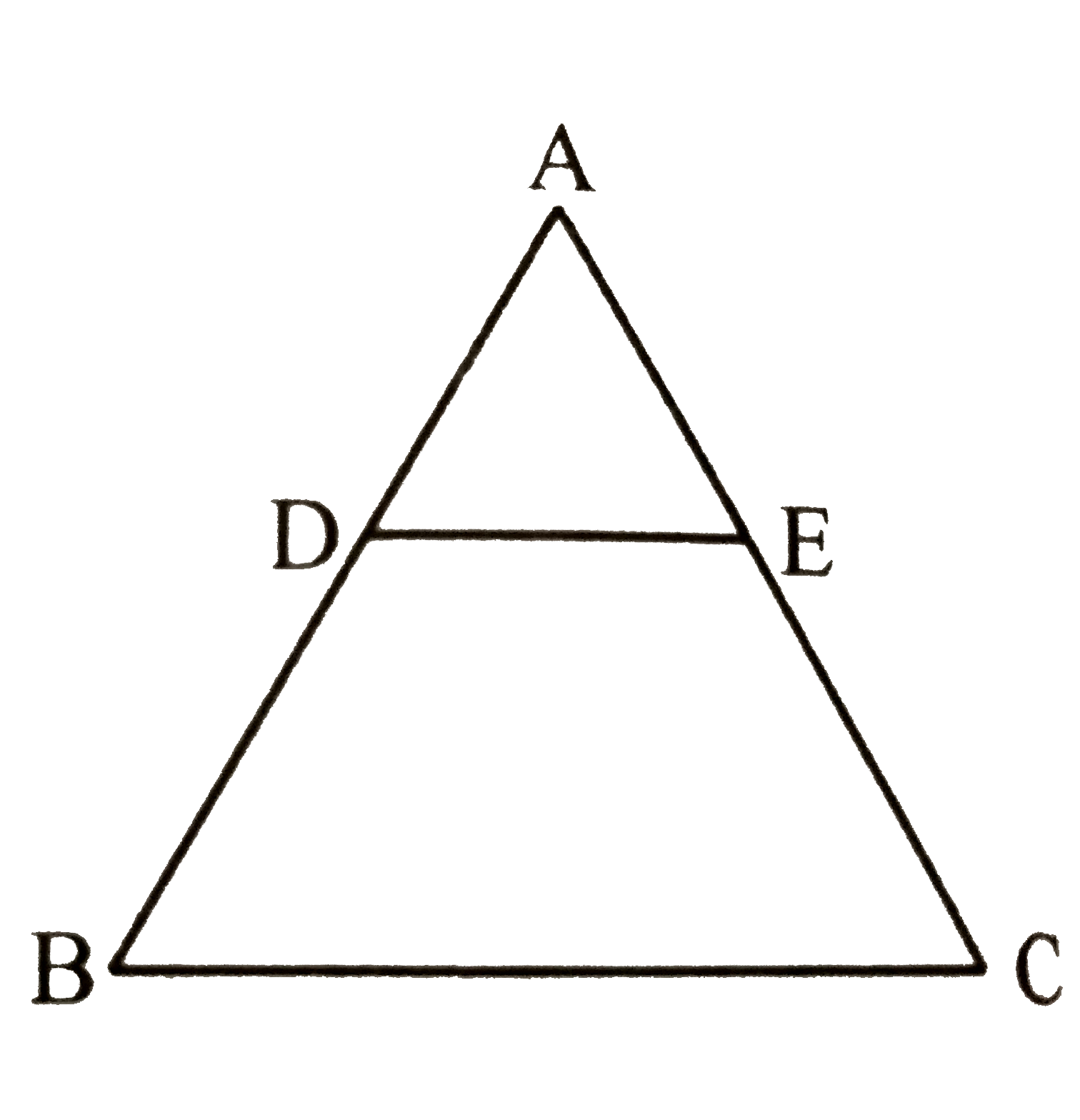
View Solutionएक `triangle ABC` की भुजाओं AB तथा AC पर क्रमशः बिंदु D तथा E है | तथा `DE||BC` और `triangle ABC` दो बराबर भागो के क्षेत्रफलो में बँटा हुआ है तो `(BD)/(AB)` का मान ज्ञात कीजिए |
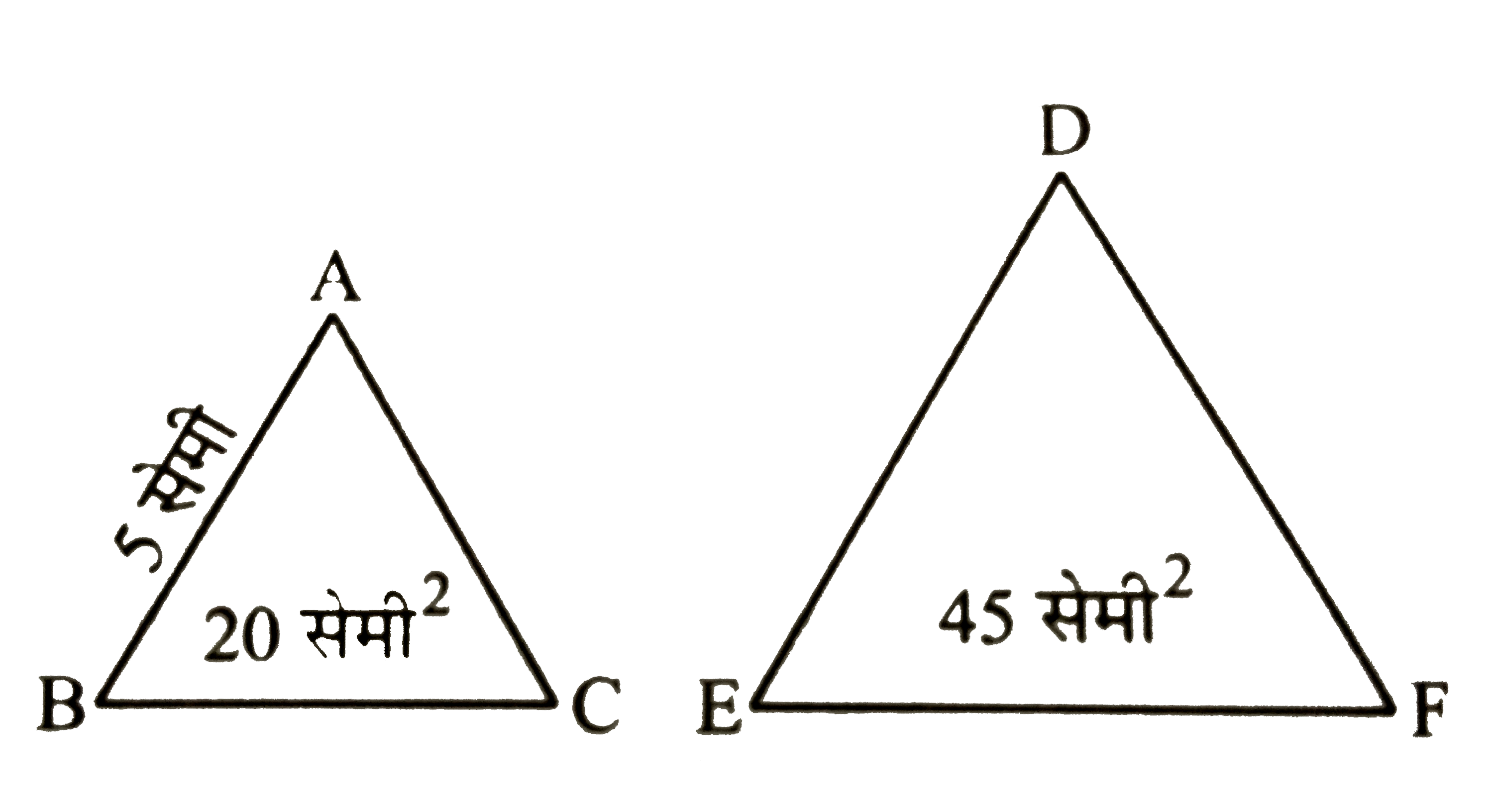
View Solutionदिये गये चित्र में,`triangle ABC ~ triangle DEF, AB = 5` सेमी `(triangle ABC)` का क्षेत्रफल = 20 सेमी`""^(2)` तथा `(triangle DEF)` का क्षेत्रफल = 45 सेमी`""^(2)` है DE ज्ञात कीजिए |
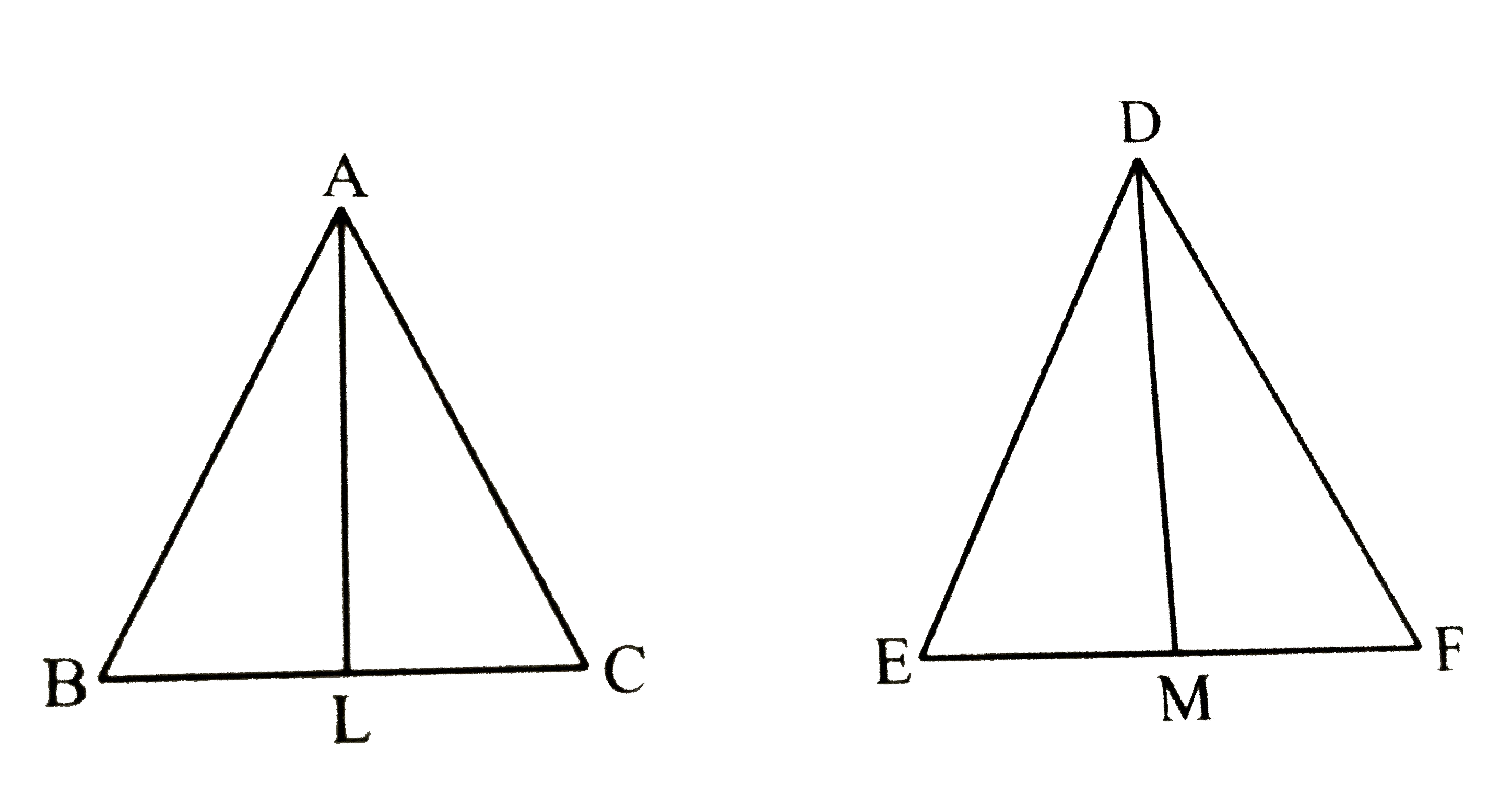
View Solutionदो समद्विबाहु त्रिभुजों की शीर्षकोण समान है और उनके क्षेत्रफलो के अनुपात 16 : 25 है तो उनकी संगत ऊँचाइयाँ के अनुपात ज्ञात कीजिए |
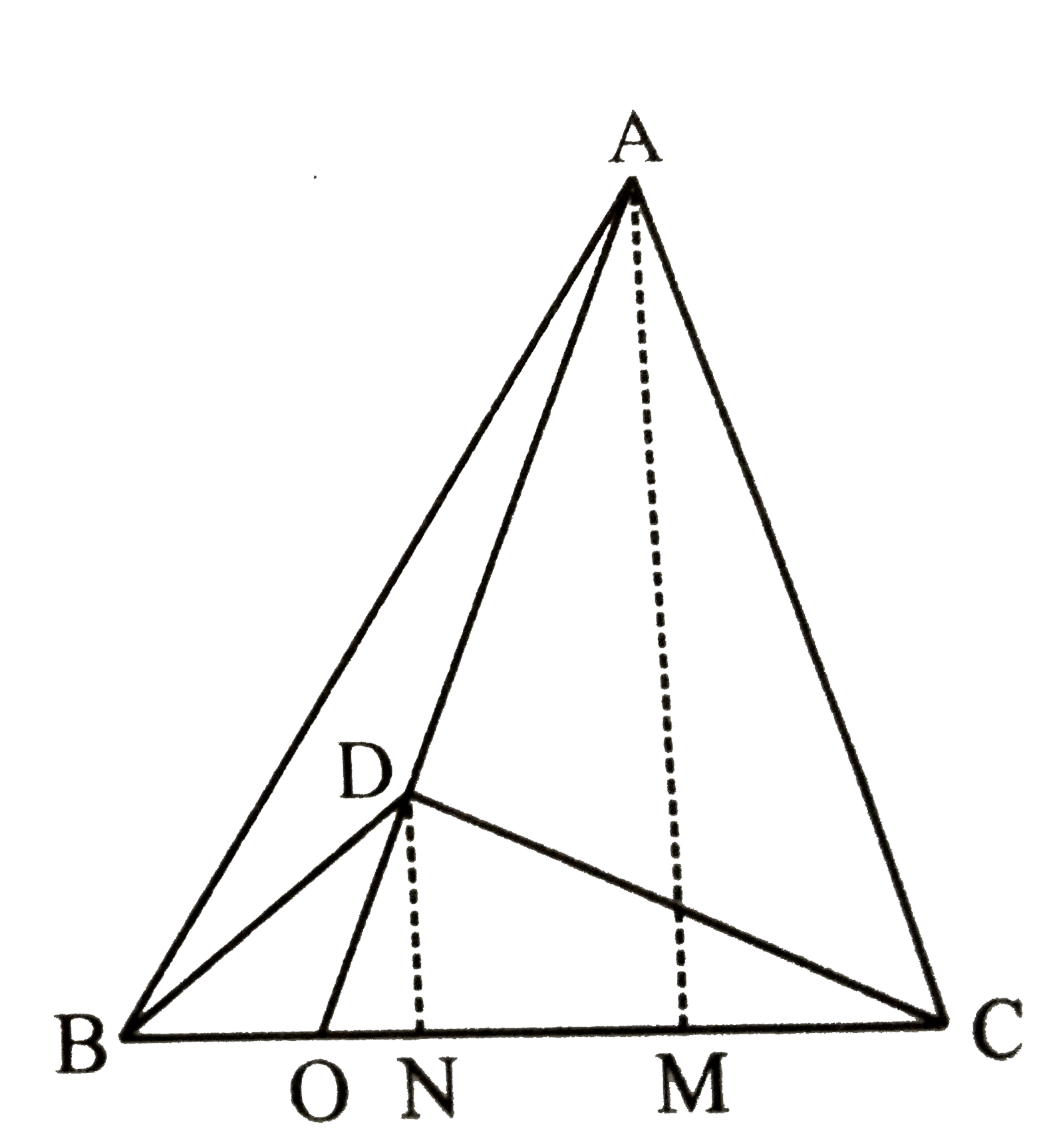
View Solutionदिये गये चित्र में, दो त्रिभुज ABC तथा DBC एक ही आधार पर स्थित है | यदि AD, BC, को O पर प्रतिच्छेद करती है तो दिखाइए कि,
`((triangle ABC)"का क्षेत्रफल")/((triangle BCD)"का क्षेत्रफल") = (AO)/(DO)`
View Solutionएक समलम्ब चतुर्भुज ABCD में, O, AC तथा BD का प्रतिच्छेद बिंदु है | `AB||CD` तथा AB = 2CD है | यदि `triangle AOB` का क्षेत्रफल = 84 सेमी`""^(2)` है तो `triangle COD` का क्षेत्रफल ज्ञात कीजिए |
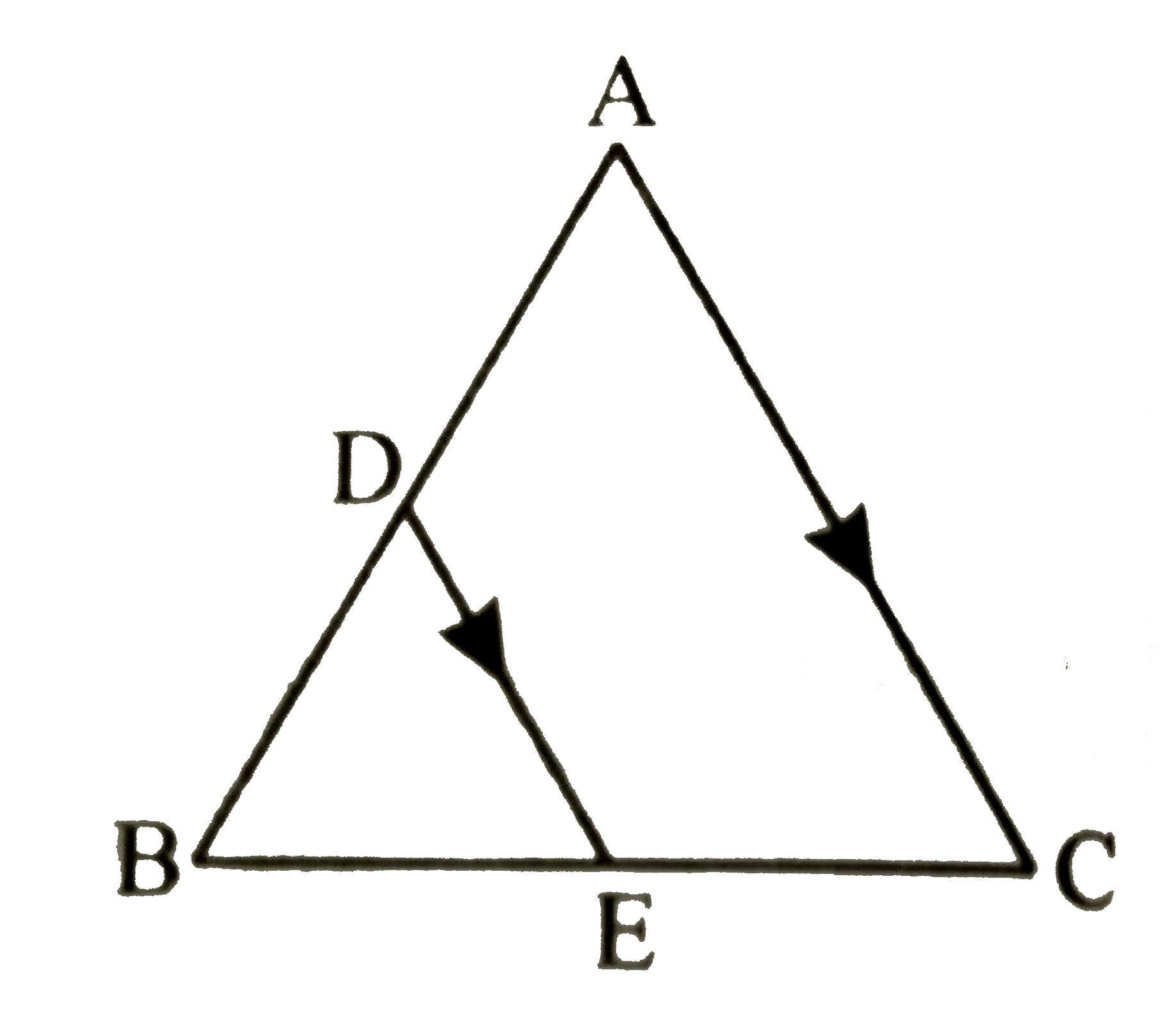
View Solutionयदि `triangle ABC` की भुजा AB पर एक बिंदु D है | तथा `AD : DB = 3:2` और BC पर एक बिंदु E है | तथा `DE||AC` है तो त्रिभुज ABC तथा त्रिभुज DBE के क्षेत्रफलो का अनुपात ज्ञात कीजिए |
View Solutionएक समकोण समद्विबाहु त्रिभुज की एक भुजा पर बने समबाहु त्रिभुज का क्षेत्रफल उसके कर्ण पर बने समबाहु त्रिभुज के क्षेत्रफल का आधा होता है |
View SolutionAD, एक समबाहु त्रिभुज ABC की एक ऊँचाई है | AD आधार का एक अन्य समबाहु त्रिभुज ADE यहाँ स्थित है | तो सिद्ध कीजिए कि `(triangle ADE)` का क्षेत्रफल : `(triangle ABC)` का क्षेत्रफल ` = 3:4`
View Solutionएक समकोण त्रिभुज की एक भुजा पर समान कोण वाला त्रिभुज खींचा गया है | जिसमे लम्ब, आधार का दोगुना है | तो सिद्ध कीजिए कि कर्ण पर त्रिभुज का क्षेत्रफल वही है जो अन्य दो त्रिभुजों के क्षेत्रफलो का योग है |
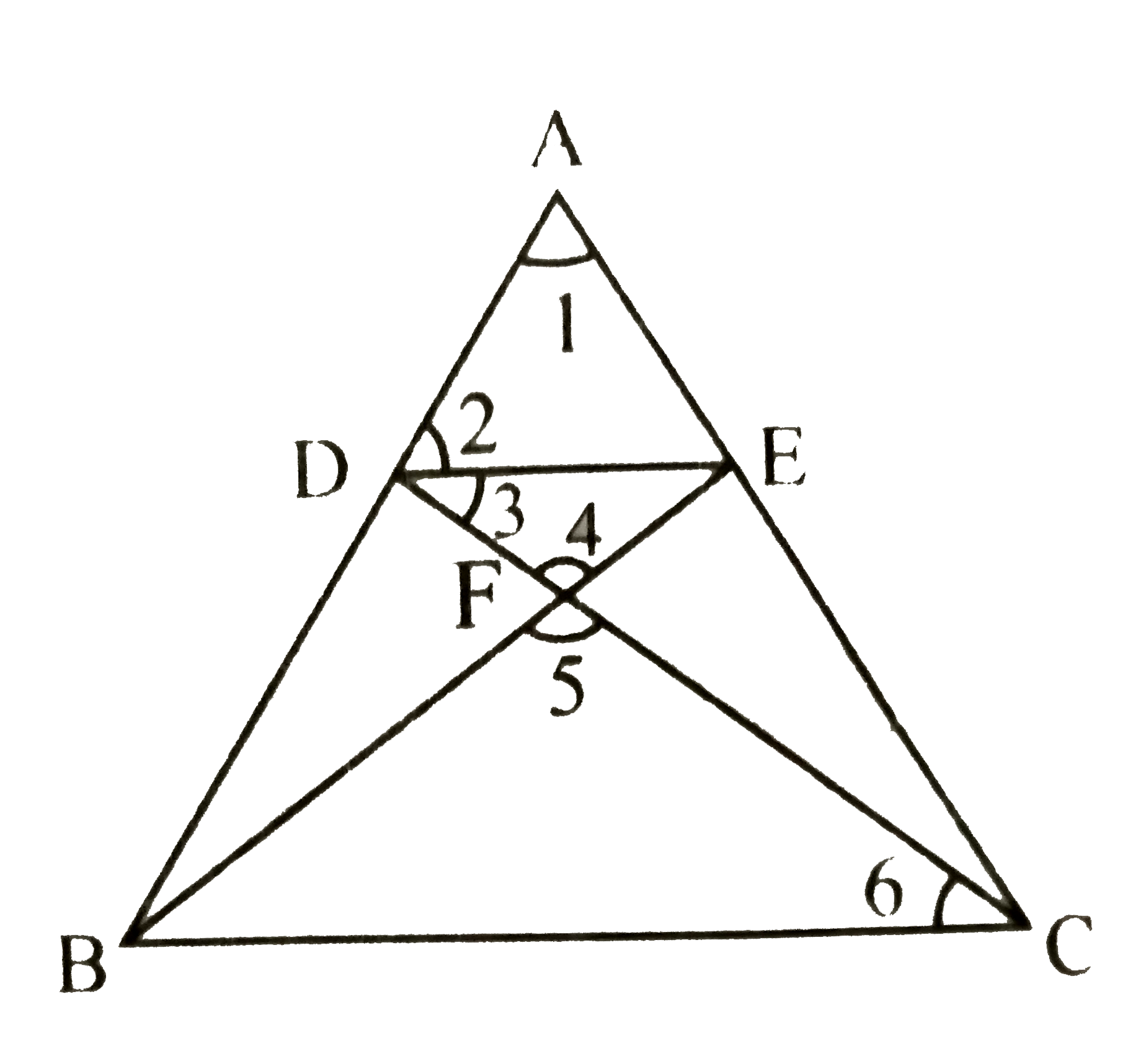
View Solutionदिये गये चित्र में , `DE ||BC` तथा `AD : DB = 7 :5` है तो
`(ar (triangle DEF))/(ar (triangle CFB))` ज्ञात कीजिए |
View Solutionनीचे कुछ त्रिभुजों की भुजाएँ दी गई है | निकालिये कि कौन-सा त्रिभुज समकोण त्रिभुज है |
(i) 8 सेमी, 15 सेमी, 17 सेमी
(ii) (2a-1) सेमी, `2sqrt(2a)` सेमी, (2a+1) सेमी
View Solution`triangle ABC` में, `angle B = 90^(@)` तथा D, BC का मध्य बिंदु है, तो सिद्ध कीजिए कि `AC^(2) = AD^(2) + 3CD^(2)`
View Solutionयदि एक `triangle ABC` की भुजाओं CA तथा CB के मध्य बिंदु क्रमशः P तथा Q है, तथा त्रिभुज C पर समकोण है | तो सिद्ध कीजिए कि
(i) `4 AQ^(2) = 4 AC^(2) + BC^(2)`
(ii) `4BP^(2) = 4BC^(2) + AC^(2)`

View Solutionएक समकोण त्रिभुज ABC,B पर समकोण है | माना कि भुजाओं AB तथा BC के मध्य बिंदु क्रमशः D तथा E है तो सिद्ध कीजिए कि :
`AE^(2) + CD^(2) = AC^(2) + DE^(2)`
View Solutionयदि `triangle ABC` एक समकोण त्रिभुज है | यह B पर समकोण है| D, BC का मध्य बिंदु है तो सिद्ध कीजिए कि
`AC^(2) = 4 AD^(2) - 3AB^(2)`
View Solutionएक `triangle ABC` में आधार BC पर AD लम्ब है जो BC को D पर प्रतिच्छेद करता है इसलिए DB = 3CD है तो सिद्ध कीजिए कि `2AB^(2) = 2AC^(2) + BC^(2)`
View Solutionएक चतुर्भुज ABCD में, `angleB = 90^(@)` है यदि `AD^(2) = AB^(2) + BC^(2) + CD^(2)` हो तो सिद्ध कीजिए कि `angle ACD = 90^(@)`
View Solutionयदि ABC एक समकोण त्रिभुज C पर समकोण है | माना कि, `BC = a, CA = b, AB = c` है| यदि AB पर C में लम्ब की लम्बाई p है तो सिद्ध कीजिए कि
(i) `cp = ab`
(ii) `(1)/(p^(2)) = (1)/(a^(2)) + (1)/(b^(2))`
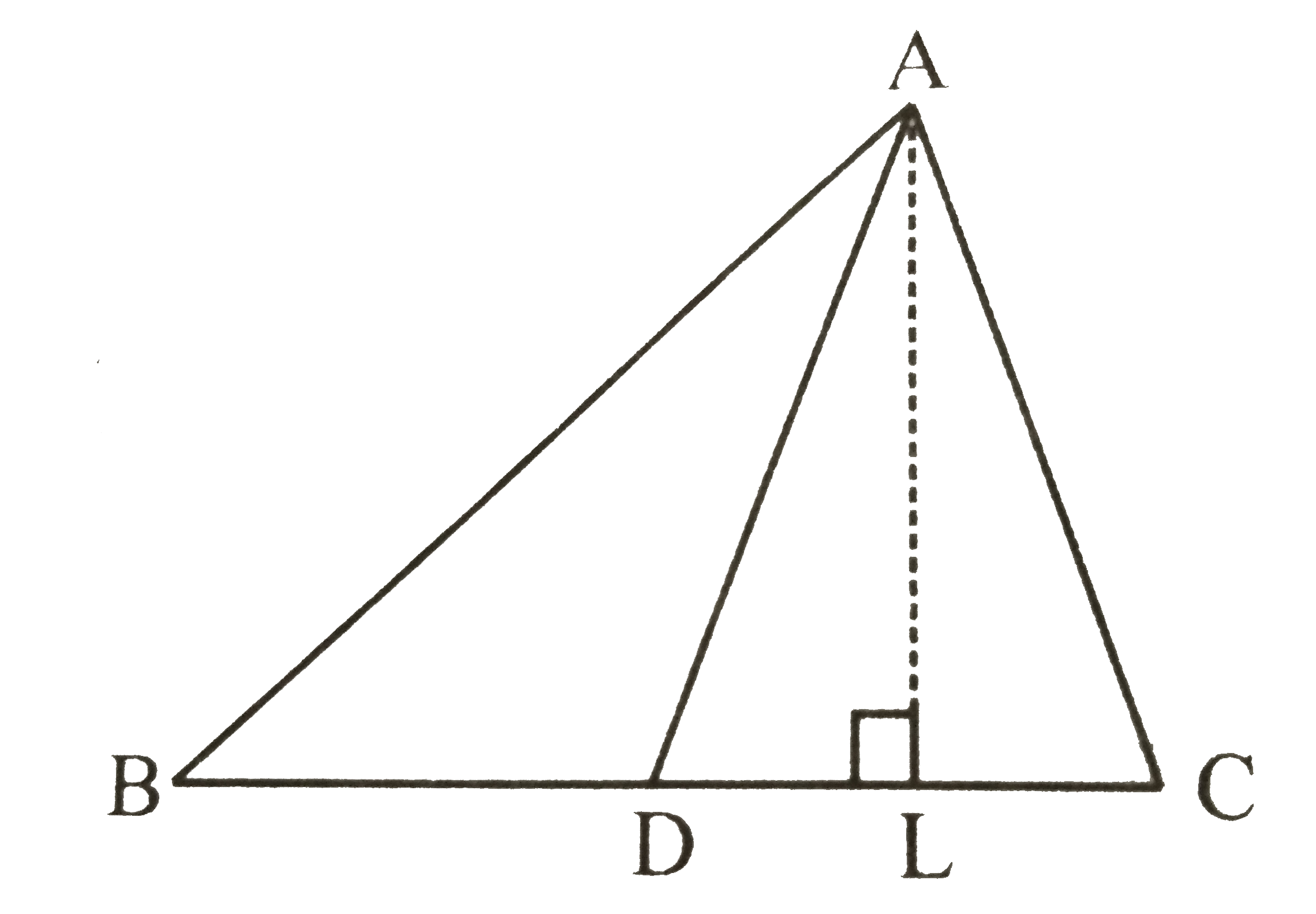
View Solution`triangle ABC` में, यदि AD माध्यिका है तो सिद्ध कीजिए कि `AB^(2) + AC^(2) = 2(AD^(2) + BD^(2))`
View Solutionसिद्ध कीजिए कि, किसी समबाहु त्रिभुज में एक भुजा के वर्ण का तीन गुना, इसकी किसी एक ऊँचाई के वर्ग के चार गुने के बराबर है |
View Solutionएक `triangle ABC` में, यदि AD, BC के लंबवत है तो सिद्ध कीजिए कि
(i) `AB^(2) + CD^(2) = AC^(2) + BD^(2)`
(ii) `AB^(2) - BD^(2) = AC^(2) - CD^(2)`
View Solutiona भुजा वाले समबाहु त्रिभुज में सिद्ध कीजिए कि :
(i) ऊँचाई ` = (asqrt(3))/(2)`
(ii) क्षेत्रफल ` = (sqrt(3))/(4) a^(2)`
View Solutionएक सबहि त्रिभुज ABC में, भुजा BC, D पर समद्विभाजित है तो सिद्ध कीजिए कि, `9AD^(2) = 7AB^(2)`
View Solutionमाना एक चतुर्भुज ABCD है तो सिद्ध कीजिए कि `AB^(2) + BC^(2) + CD^(2) + DA^(2) = AC^(2) + BD^(2)`
View Solutionदिये गये चित्र में, D तथा E, BC को समद्विभाजित करते है तो सिद्ध कीजिए कि `8 AE^(2) = 3AC^(2) + 5AD^(2)`
View Solution`triangle ABC` एक समकोण त्रिभुज है जिसका `angleA` समकोण है | इसमें अन्तःवृत्त खींचा गया है | समकोण बनाने वाली दो भुजाएँ क्रमशः 6 सेमी तथा 8 सेमी है | अन्तः वृत्त की त्रिज्या ज्ञात कीजिए |
View Solutionएक `triangle ABC` में, `AC gt BD` है | D, BC का मध्य बिन्दु है तथा `AE bot BC` तो सिद्ध कीजिए कि :
(i) `AC^(2) = AD^(2) + BC*DE + (1)/(4) BC^(2)`
(ii) `AB^(2) = AD^(2) - BC*DE + (1)/(4) BC^(2)`
View Solutionएक `triangle ABC` में, `AD bot BC` तथा `AD^(2) = BD xx CD` है तो सिद्ध कीजिए कि `triangle ABC` का समकोण त्रिभुज है |
View Solutionयदि ABC एक समद्विबाहु त्रिभुज है तथा AC = BC यदि `AB^(2) = 2AC^(2)` है तो सिद्ध कीजिए कि `triangle ABC` एक समकोण त्रिभुज है |
View Solutionयदि एक समद्विबाहु त्रिभुज ABC, B पर समकोण है | भुजा AC तथा AB पर बने दो त्रिभुज ACD तथा ABE समरूप हो तो त्रिभुज ABE और त्रिभुज ACD के क्षेत्रफलो का अनुपात ज्ञात कीजिए |
View Solutionदो खम्बो की ऊँचाई 6 मीटर तथा 11 मीटर है और समतल जमीन पर ऊर्ध्वाधर खड़े है | यदि उनके पादो के बीच की दूरी 12 मीटर है तो उनके शिरो के बीच की दूरी ज्ञात कीजिए |
View Solutionदी गई आकृति में, PR तथा PQ ज्ञात कीजिए, जब QR = 26 सेमी, PO = 6 सेमी तथा OR = 8 सेमी है |
View Solutionमाना कि एक त्रिभुज ABC है जिसमे `angleA = 90^(@)` तथा `AD bot BC` तो सिद्ध कीजिए कि `AD^(2) = BD*CD`
View Solutionसिद्ध कीजिए कि किसी समचतुर्भुज की भुजाओं के वर्गो का योग उसके विकर्णों के वर्गो के योग के बराबर होता है |
View Solutionसिद्ध कीजिए कि किसी समकोण त्रिभुज की दो भुजाओं पर बने समबाहु त्रिभुजों के क्षेत्रफलो का योग उसके विकर्ण पर बने समबाहु त्रिभुज के क्षेत्रफल के बराबर होता है |
View Solution10 मीटर लम्बी सीढ़ी जमीन से 8 मीटर ऊँची खिड़की तक पहुँचती है | दीवार की आधार से सीढ़ी के पाद की दूरी ज्ञात कीजिए |
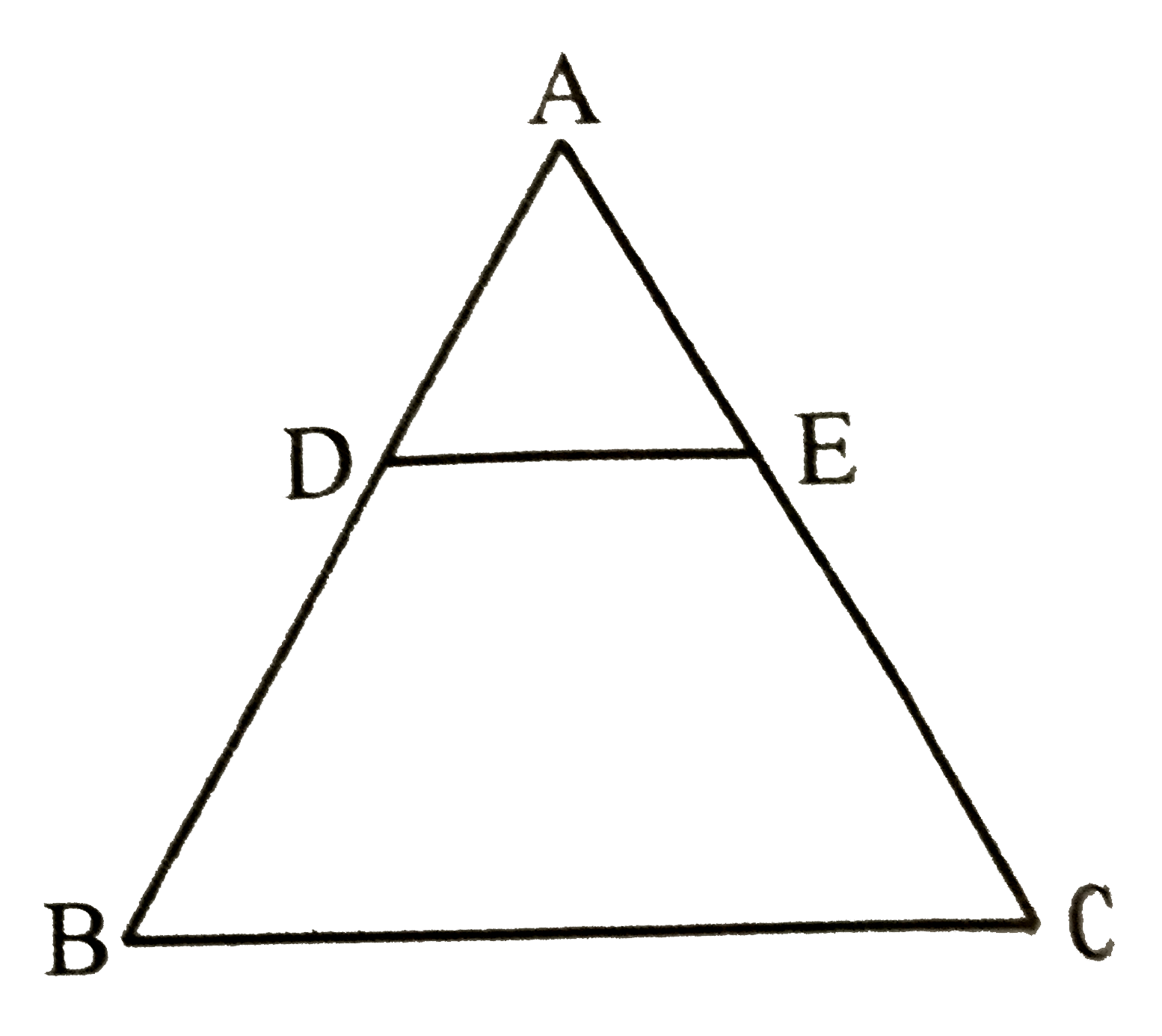
View Solutionदी गई आकृति में, बिंदु D तथा E क्रमशः AB तथा AC पर है | तथा `DE `||BC` यदि `AD = (1)/(3)BD, AE = 4.5` सेमी है तो AC ज्ञात कीजिए |
View Solution`triangle ABC` में, AC पर कोई बिंदु X है | यदि X, Y, Z, U तथा V क्रमशः AX,XC ,AB तथा BC के मध्य बिंदु है तो सिद्ध कीजिए कि `UY||VZ` तथा `UV||YZ`
View Solutionएक त्रिभुज ABC के भुजाएँ AB और AC तथा माध्यिका AD, क्रमशः अन्य त्रिभुज pQR की भुजाओं PQ और PR तथा माध्यिका PM के समानुपाती है तो सिद्ध कीजिए कि
`triangle ABC ~ triangle PQR`
View Solution`triangle ABC` में बिंदु E तथा D क्रमशः AC तथा AB पर है | तथा `angle ADE = angle B` है | यदि AD = 3.8 सेमी, AE = 3.6 सेमी, CE = 2.1 सेमी तथा BC = 4.2 सेमी है तो DE ज्ञात कीजिए |
View Solutionयदि एक समकोण त्रिभुज का क्षेत्रफल A है तथा समकोण बनाने वाली रेखा की लम्बाई b है तो सिद्ध कीजिए कि कर्ण पर लम्ब की लम्बाई `(2AB)/(sqrt(b^(2)+4A^(2)))` है |
View Solution`triangle ABC` में, `angle B = 90^(@)` तथा `BD bot AC` है | यदि DC = 7 सेमी तथा AD = 3 सेमी, तब BD की लम्बाई ज्ञात कीजिए |
View Solution`triangle ABC` में, यदि `AP bot BC` तथा `AC^(2) = BC^(2) - AB^(2)` है तब सिद्ध कीजिए कि `PA^(2) = PB xx CP`
View Solutionदी गई आकृति में, एक त्रिभुज ABC है जिसका `angleB` समकोण है तथा `BD bot AC` है यदि AD = 4 सेमी तथा CD = 5 सेमी है तो BD तथा AB ज्ञात कीजिए |
View Solution
उदाहरण questions and complete solutions for chapter त्रिभुज of SHREE BALAJI MATHS (HINDI) of Class 10