Complete Solutions to Short Answer Type Questions-II of chapter TRIANGLE of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLE |
| SUPPORT MATERIAL | Short Answer Type Questions-II |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
In the given figure, `(QR)/(QS)= (QT)/(PR) and angle1 = angle2` then prove that `trianglePQS ~ triangleTQR. `
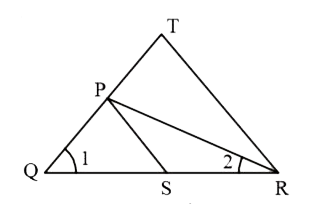 04:00View Solution
04:00View SolutionIn equilateral `triangleABC, ADbotBC.` Prove that `3BC^2= 4AD^2.`
02:34View SolutionIn the given figure `angleABC=90^(@) and CD bot AB`. Prove that `(BC^(2))/(AC^(2))=(BD)/(AD)`
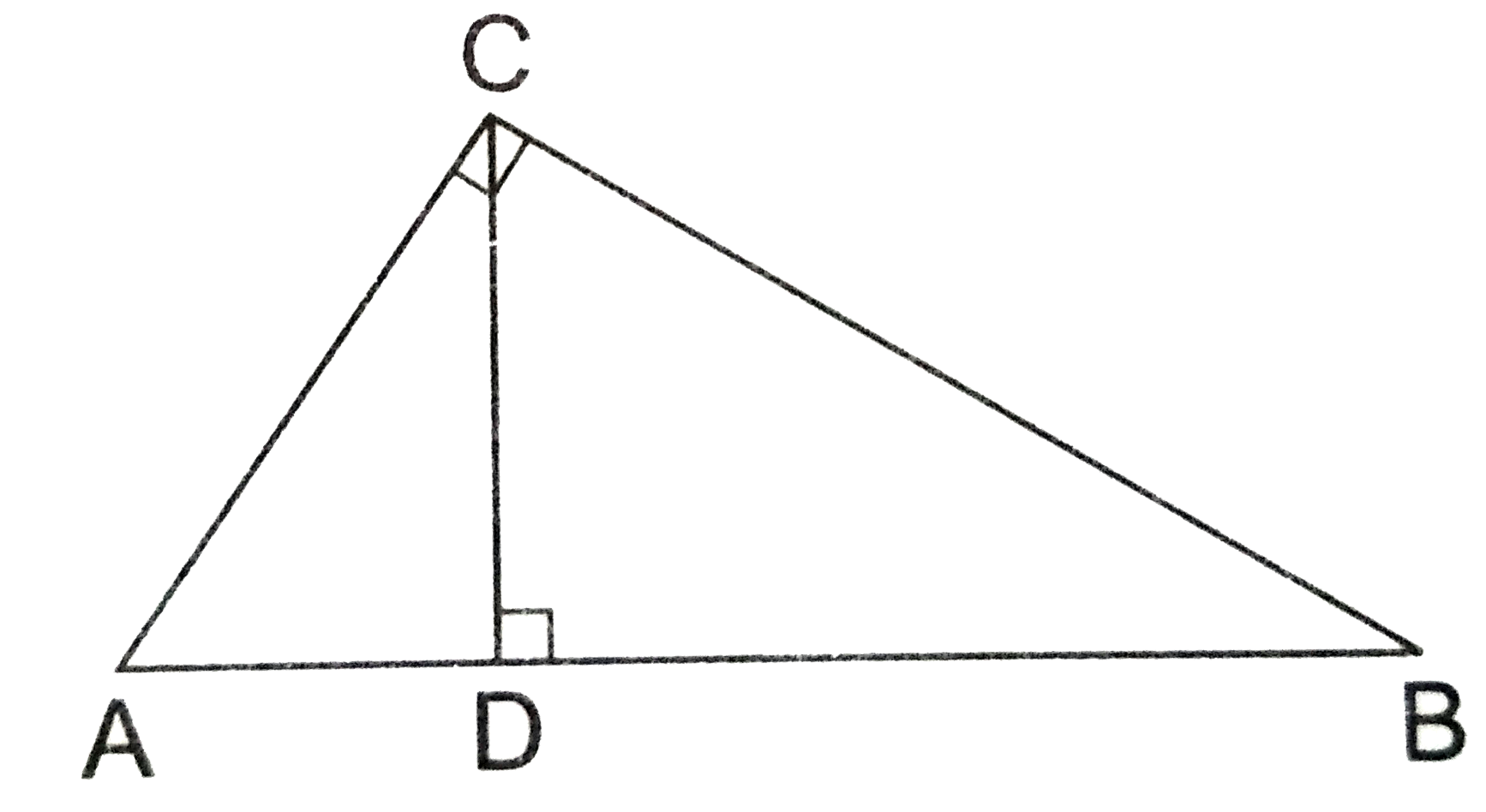 04:31View Solution
04:31View SolutionIn Fig. 4.179, ` A B C` and ` D B C` are on the same base `B C` . If `A D` and `B C` intersect at `O` , prove that `(A r e a\ ( A B C))/(A r e a\ ( D B C))=(A O)/(D O)` (FIGURE)
03:10View SolutionIf AD and PS are medians of `triangleABC and trianglePQR` respectively where `triangleABC ~ trianglePQR,` Prove that `(AB)/(PQ)=(AD)/(PS)`.
03:35View SolutionIn the given figure, DE || AC. Which of the following is correct? `x=(a+b)/(ay) or x=(ay)/(a+b)`
 02:24View Solution
02:24View SolutionProve that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
05:22View SolutionA street light bulb is fixed on a pole 6 m above the level of the street. If a women of height 1.5 m casts a shadow of 3 m, then find how far she is away from the base of the pole.
03:22View SolutionTwo poles of height a metres and `b` metres are `p` metres apart. Prove that the height of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is given by `(a b)/(a+b)` metres.
07:21View SolutionIn the given figure AB || PQ || CD, AB=x, CD=y and PQ=z. Prove that `1/x+1/y=1/z`
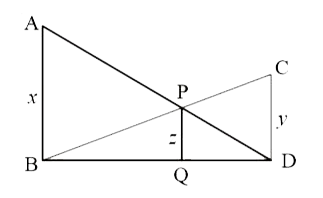 03:09View Solution
03:09View SolutionIn the given figure `(PS)/(SQ)=(PT)/(TR) and anglePST = anglePRQ.` Prove that PQR is an isoscles triangle.
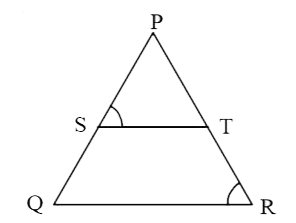 03:50View Solution
03:50View SolutionIn the figure, a point O inside `triangleABC` is joined to its vertices. From a point D on AO, DE is drawn parallel to AB and from a point E on BO, EF is drawn parallel to BC. Prove that DF || AC.
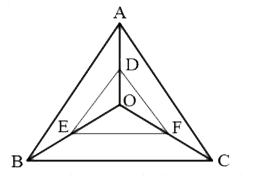 02:53View Solution
02:53View SolutionTwo triangles `B A Ca n dB D C` , right angled at `Aa n dD` respectively, are drawn on the same base `B C` and on the same side of `B C` . If `A C` and `D B` intersect at `P ,` prove that `A PxP C=D PxP Bdot`
02:17View SolutionThe Hypotenuse of a right triangle is 25 cm and out of the remaining two sides, one is larger than the other by 5 cm, find the lenghts of the other two sides.
03:40View SolutionIn the given figure DE || AC and `(BE)/(EC)=(BC)/(CP)`. Prove that DC || AP.
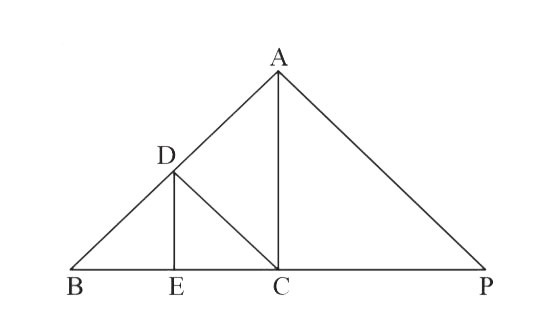 03:04View Solution
03:04View SolutionIn a quadrilateral ABCD, `angleB=90^(@) and AD^(2)= AB^(2) + BC^(2)+CD^(2)` prove that ` angleACD= 90^(@)` .
02:05View SolutionIn the given figure, DE || BC, DE= 3 cm, BC = 9 cm and ar (DADE) = `30cm^2`. Find ar (BCED).
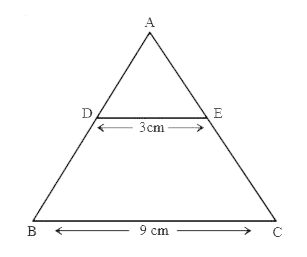 03:41View Solution
03:41View SolutionIn an equilateral triangle ABC, D is a point on side BC such that `B D=1/3B C`. Prove that `9A D^2=7A B^2`.
07:33View SolutionIi `DeltaPQR`, PD`bot`QR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=d, then prove that (a+b)(a-b)=(c+d)(c-d).
02:48View SolutionThe ratio of the the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides/altitudes.
07:50View SolutionIn the given figure, the line segment XY is Parallel to AC of ΔABC and it divides the triangle into two parts of equal areas. Prove that `(AX)/(AB)=(sqrt2-1)/(sqrt2)`
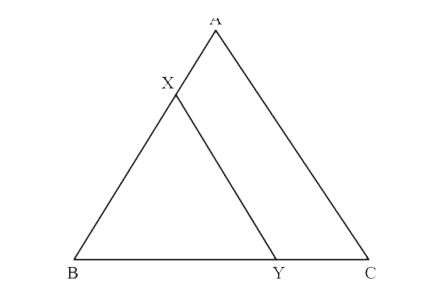 04:51View Solution
04:51View SolutionThrough the vertex D of a parallelogram ABCD, a line is drawn to intersect the sides BA and BC produced at E and F respectively. Prove that `(DA)/(AE)= (FB)/(BE)= (FC)/(CD)`
04:46View SolutionTheorem 6.9 : In a triangle, if square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
08:08View SolutionProve that is a right angle triangle, the square of the hypotenuse is equal the sum of the squares of other two sides.
04:40View SolutionTheorem 6.1 : If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
08:03View Solution
Short Answer Type Questions-II questions and complete solutions for chapter TRIANGLE of CBSE COMPLEMENTARY MATERIAL MATHS (HINGLISH) of Class 10
