Complete Solutions to बहुविकल्पीय-प्रश्न of chapter त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | त्रिभुज |
| DEEPAK PUBLICATION | बहुविकल्पीय-प्रश्न |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
यदि दो त्रिभुजों में संगत कोण बराबर हों, तो उनकी संगत भुजाएँ एक ही अनुपात में (समानुपाती) होती हैं और इसलिए ये समरूप होते हैं। सिद्ध करें।
View Solutionएक त्रिभु की एक भुजा के समानान्तर खींची गई रेखा अन्य दो भुजाओं की जिन दो बिन्दुओं पर प्रतिच्छेद करती है , वे बिन्दु उन भुजाओं को समान अनुपात में विभाजित करते है । यह प्रमेय किस नाम से जानी जाती है ?
View Solutionसिद्ध कीजिए कि यदि एक रेखा, एक त्रिभुज की किन्ही दो भुजाओं को समान अनुपात विभाजित करती है तो रेखा को तीसरी भुजा के समान्तर होना चाहिए |
View Solutionदी गई आकृति में, यदि DE `|| `AB हो तो x का मान क्या होगा ?
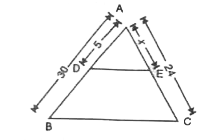
View Solutionदी गई आकृति में, यदि DE `|| `AB हो तो x का मान क्या होगा ?

View Solutionत्रिभुज की किसी भुजा के मध्य-बिन्दु से दूसरी भुजा के समान्तर खींची गई ।रेखा तीसरी भुजा को ......... करती है।
View Solutionरिक्त स्थानों की पूर्ति कीजिये -
सभी वृत्त....................होते है।
View Solution`triangle`ABC की भुजाएँ AB व AC पर क्रमश: D व E बिंदु इस प्रकार स्थित है कि DE||BC हो तो
यदि AD=6 सेमी., DB=9 सेमी. और AE=8 सेमी. हो तो AC का मान ज्ञात कीजिये।
View Solutionरिक्त स्थानों की पूर्ति कीजिये -
सभी...............त्रिभुज समरूप होते है।
View Solutionभुजाओं की समान संख्याओं वाले दो बहुभुज समरूप होते है , यदि (a) उनके संगत कोण ………... हो , तथा (b) उनकी संगत भुजाएँ ……………. हों ।
View Solutionदी गई आकृति में, यदि DE `|| `AB हो तो x का मान क्या होगा ?

View Solutionदी गई आकृति में `AB ||CD`, तो x का मान ज्ञात करें
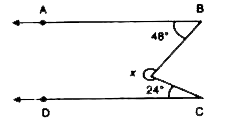
View Solution`DeltaABC` में, AB तथा AC पर क्रमशः D तथा E बिंदु इस प्रकार है कि DE||BC यदि `frac{AD}{DB}=frac{3}{4}` तथा AC=15 `"सेमी"@` निम्न से AE का मान ज्ञात कीजिए:
View Solutionरिक्त स्थानों को भरें:
किसी त्रिभुज की दो भुजाओं के मध्य बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर और ................... होती है।
View Solutionसंलग्न आकृति AABC में, DE || BC तथा `(AD)/(DB) = 3/5` यदि AC = 4.8 cm हो तो AE का मान होगा|
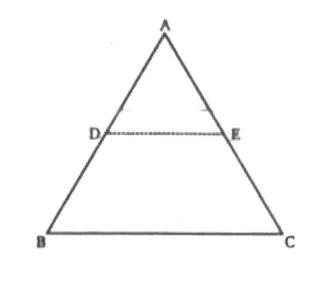
View Solutionदी गई आकृति में `triangleODC ~ triangleOAB, triangleBOC = 100^(@), angleODC = 60^(@)`, तो `angleOAB` का मान है:
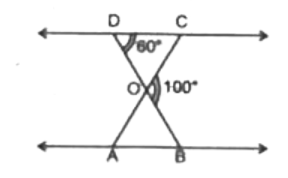
View Solution`Delta ABC` में भुजाओ AB और AC पर बिंदु D और E इस प्रकार है कि DE||BC है
(i) यदि `(AD)/(DB)=2/3` और AC=18 सेमी , तो AE ज्ञात कीजिये
(ii) यदि AD=4 सेमी , DB=4. 5 सेमी और AE=8 सेमी तो AC ज्ञात कीजिये
(iii)यदि AD=x , DB=x-2 , AE=(x+2) और EC=(x-1), तो x का मान ज्ञात कीजिये
(iv) यदि AD=4x-3, AE=8x-7, BD=3x-1 और तो CE=5x-3 तो x का मान ज्ञात कीजिये
View Solution10.5 cm लम्बे रेखाखण्ड को 3:4 के आन्तरिक अनुपात में विभाजित करने पर छोटे भाग की लम्बाई होगी|
View Solutionयदि दो त्रिभुजों में संगत कोण बराबर हों तो त्रिभुजें समरूप होती हैं क्योंकि उनकी संगत भुजाएँ आनुपातिक होती हैं, इस समरूपता को कहा जाता है-
View Solutionयदि दो त्रिभुजों की भुजाएँ आनुपातिक हों तो वे त्रिभुज समरूप कहलाते हैं क्योंकि उनके संगत कोण बराबर होते हैं, इस समरूपता को कहा जाता है-
View Solutionआकृति में , `angleX` का मान बताइए।
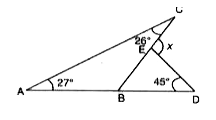
View Solutionत्रिभुजों के युग्मों में से कौन-सा युग्म समरूप नहीं है?
View Solutionदी गई आकृति में `triangleODC ~ triangleOAB, angleBOC = 125^(@), angleODC = 70^(@)` तो `angleOAB` का मान है :
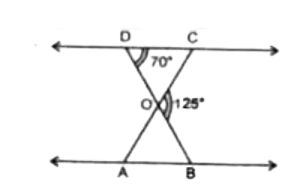
View Solutionदो समरूप त्रिभुजों के परिमाप 30 सेमी और 20 सेमी है यदि पहले त्रिभुज की एक भुजा 12 सेमी है तो दूसरे त्रिभुज की संगत भुजा ज्ञात कीजिये
View Solutionसंलग्न आकृति में, यदि EB = 2 cm, AE = 5 cm, AF =x, FC=x-1 तथा EF || BC, तो x का मान होगा |
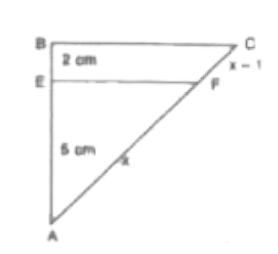
View Solutionयदि दो समरूप त्रिभुजों कि भुजाओं का अनुपात 3 : 5 है तो इन त्रिभुजों के क्षेत्रफलों का अनुपात …… है
View Solutionदो समरूप त्रिभुजों के क्षेत्रफल का अनुपात `64:121` है, तो उनकी भुजाओं में अनुपात होगा :
View Solutionकुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं :
( 1 ) 3 cm , 6 cm , 8 cm
( ii ) 5 cm , 13 cm , 12 cm
( ii ) 5 cm , 8 cm , 10 cm
इनमें से समकोण त्रिभुज है :
View Solutionयदि दो त्रिभुज ABC और DEF इस प्रकार है कि `(AB)/(DE)=(BC)/(EF)=(CA)/(FD)=(2)/(5)" तो "ar (Delta ABC): ar (Delta DEF)=`
View Solutionयदि दो समरूप त्रिभुजों की भुजाओं का अनुपात `2:3` है , तो उनके क्षेत्रफल का अनुपात है:
View Solutionदो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 64 : 121 है , तो उनकी भुजाओं का अनुपात होगा :
View Solutionसिद्ध कीजिए कि किसी वर्ग की एक भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल, इसके विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
View Solutionमान लीजिए `Delta ABC ~ Delta DEF` है और इनके क्षेत्रफल क्रमशः `64 cm^(2)` और `121 cm^(2)` है यदि EF=15.4 cm हो तो BC ज्ञात कीजिए
View Solutionदि दो समरूप त्रिभुजों की भुजाओं का अनुपात `3 : 2` है, तो उनके क्षेत्रफलों का अनुपात है:
View Solutionयदि `triangle ABC ~ triangle DEF` तथा `(triangle ABC)` का क्षेत्रफल = 16 सेमी`""^(2),(triangle DEF)` का क्षेत्रफल = 25 सेमी`""^(2)` तथा BC = 2.3 सेमी है तो EF ज्ञात कीजिए |
View Solutionविश्लेषिक विधि से सिद्ध कीजिए कि एक समकोण त्रिभुज में कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर होता है ।
View Solutionरिक्त स्थानों को उचित उत्तर से भरिए-
यदि किसी त्रिभुज की किसी एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो, तो पहली भुजा के सामने का कोण .... होता है।
View Solutionत्रिभुज ABC और DEF समरूप हैं। यदि AC = 19 cm और DF = 8 cm, तो दोनों त्रिभुजों के क्षेत्रफलों का अनुपात है-
View Solutionएक सीढ़ी इस प्रकार रखी है कि इसका निचला सिरा दीवार से 5 मी. की दूरी पर है और ऊपरी सिरा खिड़की तक पहुँचता है , जो भूमि से 12 मी. ऊपर है। सीढ़ी की लंबाई ज्ञात कीजिए।
View Solutionयदि एक समबाहु त्रिभुज ABC इस प्रकार है कि `AD bot BC` है, तो `AD^(2)=`
View Solutionएक सीढ़ी किसी दीवार पर इस प्रकार टिकी हुई है कि इसका निचला सिरा दीवार से 2.5 m की दूरी पर है तथा इसका ऊपरी सिरा भूमि से 6 m की ऊंचाई पर बनी एक खिड़की तक पहुचँता है । सीढ़ी की लम्बाई ज्ञात कीजिए ।
View Solution20 m लंबी एक सीढ़ी एक भवन की खिड़की पर पहुँचती है, जो भूमि से 16 m की ऊँचाई पर है। भवन से सीढ़ी के निचले सिरे की दूरी होगी
View Solutionदो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात `4:5` है, तो उनकी संगत भुजाओं का अनुपात है :
View Solutionकुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं :
( 1 ) 3 cm , 6 cm , 8 cm
( ii ) 5 cm , 13 cm , 12 cm
( ii ) 5 cm , 8 cm , 10 cm
इनमें से समकोण त्रिभुज है :
View Solutionएक आदमी उत्तर की ओर 7m जाता है और फिर पूर्व की ओर 24 m जाता है। बताइए कि वह प्रारंभिक बिंदु से कितनी दूरी पर है ?
View Solutionएक सीढ़ी सड़क के एक और 12 मी ऊँची खिड़की एक पहुँचती है। सीढ़ी के निचले सिरे को हटाए बिना वह सीढ़ी उसी सड़क के दुदृ और 9 मी ऊँची खिड़की तक पहुँचती है । यदि सीढ़ी कि लम्बाई 15 मी हो तो सड़क कि चौड़ाई मालूम कीजिए ।
View Solutionएक व्यक्ति एक निश्चित बिंदु से प्रथम पूर्व की ओर कुछ दूर चलता है तदोपरांत 12 m उत्तर की ओर जाता है और इस प्रकार वह अपनी प्रथम स्थिति से 13 m की दूरी पर पहुँचता है। उसके द्वारा पूर्व दिशा में चली दूरी होगी-
View Solution6 मी. तथा 11 मी. ऊंचाई के दो खंभे एक समतल मैदान में गड़े हैं। यदि उनके बीच की दूरी 18 मी. हो, तो उनकी ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
View Solution5 m तथा 8 m ऊँचाई के दो खंभे एक समान तल पर खड़े हुए हैं। यदि उनके निचले सिरों के मध्य की दूरी 4m हो तो उनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।
View Solution`triangleABC` एक समद्विबाहु समकोण त्रिभुज है। यदि `angleABC = 90^o` तथा `AB = 5sqrt(2) cm` हो तो AC का मान होगा-
View Solutionकिसी समबाहु त्रिभुज में , सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलंब के वर्ग के चार गुने के बराबर होता है ।
View SolutionABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है-
View Solution`triangleABC` में AD, `angleBAC` का समद्विभाजक है। यदि AB=6cm,AC=5cm and BD=3cm हो तो DC का मान होगा-
View Solutionयदि आकृति में `AD, angleA` को समद्विभाजित करता है तथा AB = 12 cm, AC = 20 cm और BD = 5 cm हो, तो CD का मान होगा-
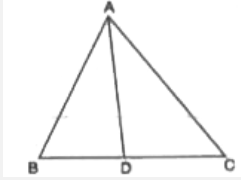
View Solutionदो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात `5:3` है, तो उनके संगत भुजाओं का अनुपात है :
View Solutionकुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं:
(i) 3 cm, 4 cm, 6 cm (ii) 5 cm, 12 cm, 16 cm (iii) 8 cm, 15 cm, 17 cm
इनमें से समकोण त्रिभुज है-
View Solution`triangleABC` में `AD, angleBAC` का समद्विभाजक है। यदि AB = 10 cm, AC =14cm व BD = 2.5 cm हो तो DC की लंबाई होगी-
View Solutionदो समरूप त्रिभुजों की संगत भुजाओं का अनुपात 4: 9 है। इन त्रिभुजों के क्षेत्रफलों का अनुपात है:
View Solution
बहुविकल्पीय-प्रश्न questions and complete solutions for chapter त्रिभुज of DEEPAK PUBLICATION of Class 10