Complete Solutions to परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न of chapter त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | त्रिभुज |
| DEEPAK PUBLICATION | परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
यदि आकृति (1) और (i) में, PQ || BC हो, तो (i) में QC और (ii) में AQ ज्ञात कीजिए-
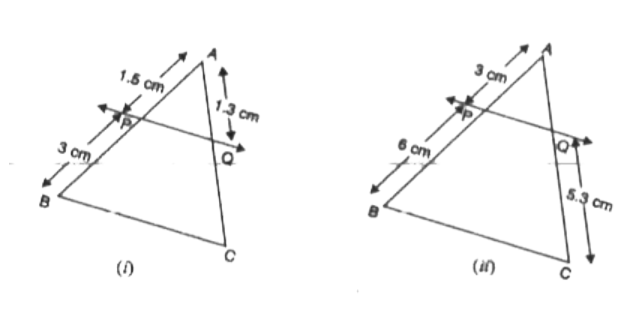
View SolutionABCD एक समलम्ब हैं जिसमे AB ||DC हैं । असमान्तर भुजाओं AD और BC पर क्रमशः बिन्दु E और F इस प्रकार स्थित हैं कि EF भुजा AB के समान्तर हैं दर्शाइए कि `(AE)/(ED)=(EF)/(FC)` हैं ।
View Solutionसिद्ध कीजिए कि समलंब कि समान्तर भुजाओ के समांतर खींची गई रेखा असमंतर भुजाओ को आनुपातिकता विभाजित करती है ।
View Solutionयदि दो समानान्तर रेखाओं को एक तिर्यक रेखा प्रतिच्छेदित करती है तो, सिद्ध कीजिए कि तिर्यक रेखा के एक ही ओर स्थित अन्तः कोनो की अर्धक रेखायें परस्पर समकोण पर प्रतिच्छेद करती है।
View Solution7 .6 सेमी लम्बा एक रेखाखंड खीचिए और इसे 5 : 8 के अनुपात में विभाजित कीजिए । दोनों भागो को मापिए ।
View Solutionसंलग्न आकृति में, यदि EB = 2 cm, AE = 5 cm, AF =x, FC=x-1 तथा EF || BC, तो x का मान होगा |
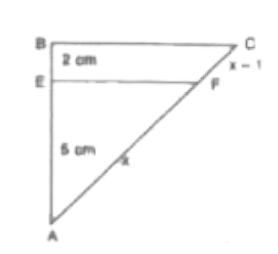
View Solutionसंलग्न आकृति में, `triangleEDC ~ triangleEBA, angleBEC = 115^(@)` और `angleEDC=70^(@)` है। `angleDEC, angleDCE, angleEAB, angleAEB` और `angleEBA` ज्ञात कीजिए।
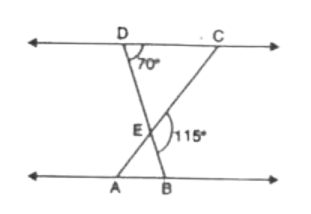
View Solutionसंलग्न आकृति में, यदि PS || QR है, तो सिद्ध कीजिए कि `anglePOS ~ triangleROQ` है।
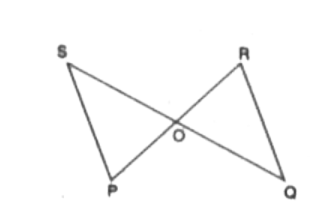
View Solutionदो समरूप त्रिभुजों के परिमाप 30 सेमी और 20 सेमी है यदि पहले त्रिभुज की एक भुजा 12 सेमी है तो दूसरे त्रिभुज की संगत भुजा ज्ञात कीजिये
View Solutionसंलग्न आकृति में, `(OA)/(OC) = (OD)/(OB)` है। सिद्ध कीजिए कि `angleA = angleC` और `angleB = angleD` है।

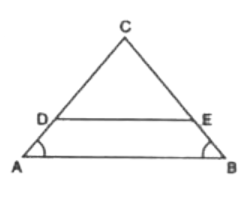
View Solutionसंलग्न आकृति में, `angleA = angleB` और AD = BE है। सिद्ध कीजिए कि DE || AB है।
View Solutionएक सीढ़ी किसी दीवार पर इस प्रकार टिकी हुई है कि इसका निचला सिरा दीवार से 2.5 m की दूरी पर है तथा इसका ऊपरी सिरा भूमि से 6 m की ऊंचाई पर बनी एक खिड़की तक पहुचँता है । सीढ़ी की लम्बाई ज्ञात कीजिए ।
View Solutionपृथ्वी से 15 m ऊँचाई पर भवन की एक खिड़की तक 17 m लम्बाई की एक सीढ़ी पहुँचती है। सीढ़ी के पाद से भवन की दूरी ज्ञात कीजिए।
View Solutionएक व्यक्ति पूरब की ओर 10 m और फिर उत्तर की ओर 30 m जाता है। प्रारंभिक बिंदु से उसकी दूरी ज्ञात कीजिए।
View Solution90 सेमी की लम्बाई वाली एक लड़की बल्ब लगे एक खंम्बे के आधार से परे 1.2 मी /सेकण्ड की चाल से चल रही है । यदि बल्ब भूमि से 3.6 मी की ऊँचाई पर है , तो 4 सेकण्ड बाद उस लड़की की छाया की लम्बाई ज्ञात कीजिए ।
View Solutionआयतन ABCD के अंदर स्थित O कोई बिन्दु है । सिद्ध कीजिए कि `OB^(2)+OD^(2)=OA^(2)+OC^(2)` है ।
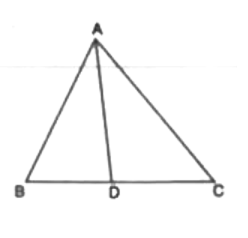
View Solutionयदि आकृति में दिए हुए `triangleABC` में AB = 5 cm, AC = 10 cm, BD = 1.5 cm और CD = 3.5 cm हो तो जाँच कीजिए कि क्या AD, `angleA` का समद्विभाजक है।
View Solutionदो खंभे जिसकी ऊंचाईयों 7 मी और 12 मी हैं, एक समतल भूमि पर खड़े है यदि इनके निचले सिरों के बीच की दूरी 12 मी है, तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए I
View Solution`triangleABC` एक समद्विबाहु समकोण त्रिभुज है। यदि `angleABC = 90^o` तथा `AB = 5sqrt(2) cm` हो तो AC का मान होगा-
View Solutionचतुर्भुज ABCD का विकर्ण `BD,angleB` और `angleD` को समद्विभाजित करता है । सिद्ध कीजिए कि `(AB)/(BC)=(DA)/(CD)`.
View Solutionदो समरूप त्रिभुजों ABC और PQR के क्षेत्रफल क्रमशः `36 cm^2` तथा `64 cm^2` हैं। यदि BC=4.2 cm हो तो QR ज्ञात कीजिए।

View Solution
परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्न questions and complete solutions for chapter त्रिभुज of DEEPAK PUBLICATION of Class 10