Complete Solutions to प्रश्नावली 6.6 (ऐच्छिक) of chapter त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | त्रिभुज |
| DEEPAK PUBLICATION | प्रश्नावली 6.6 (ऐच्छिक) |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
आकृति में PS कोण QPR का समद्विभाजक है । सिद्ध कीजिए कि `(QS)/(SR)=(PQ)/(PR)` है ।
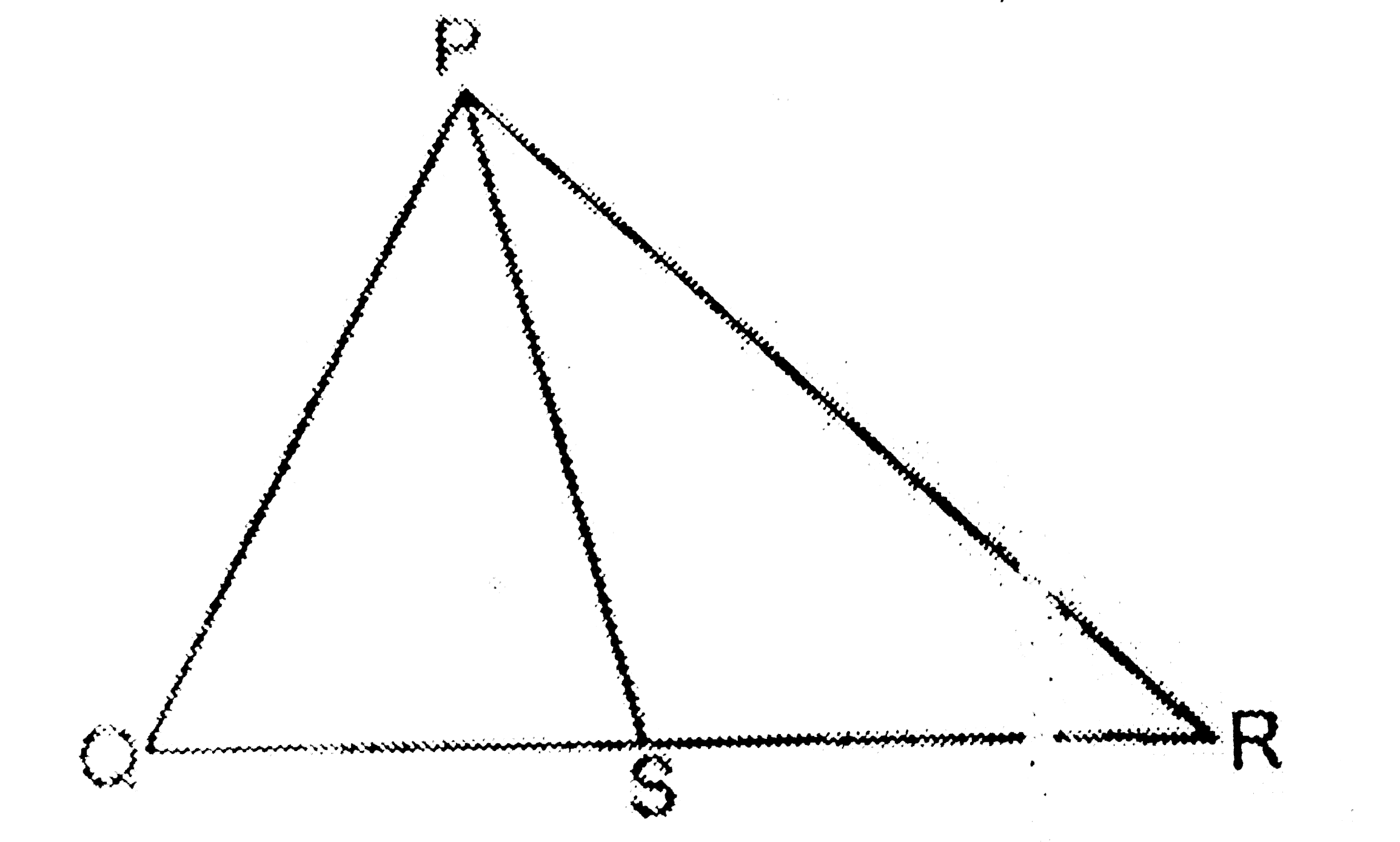
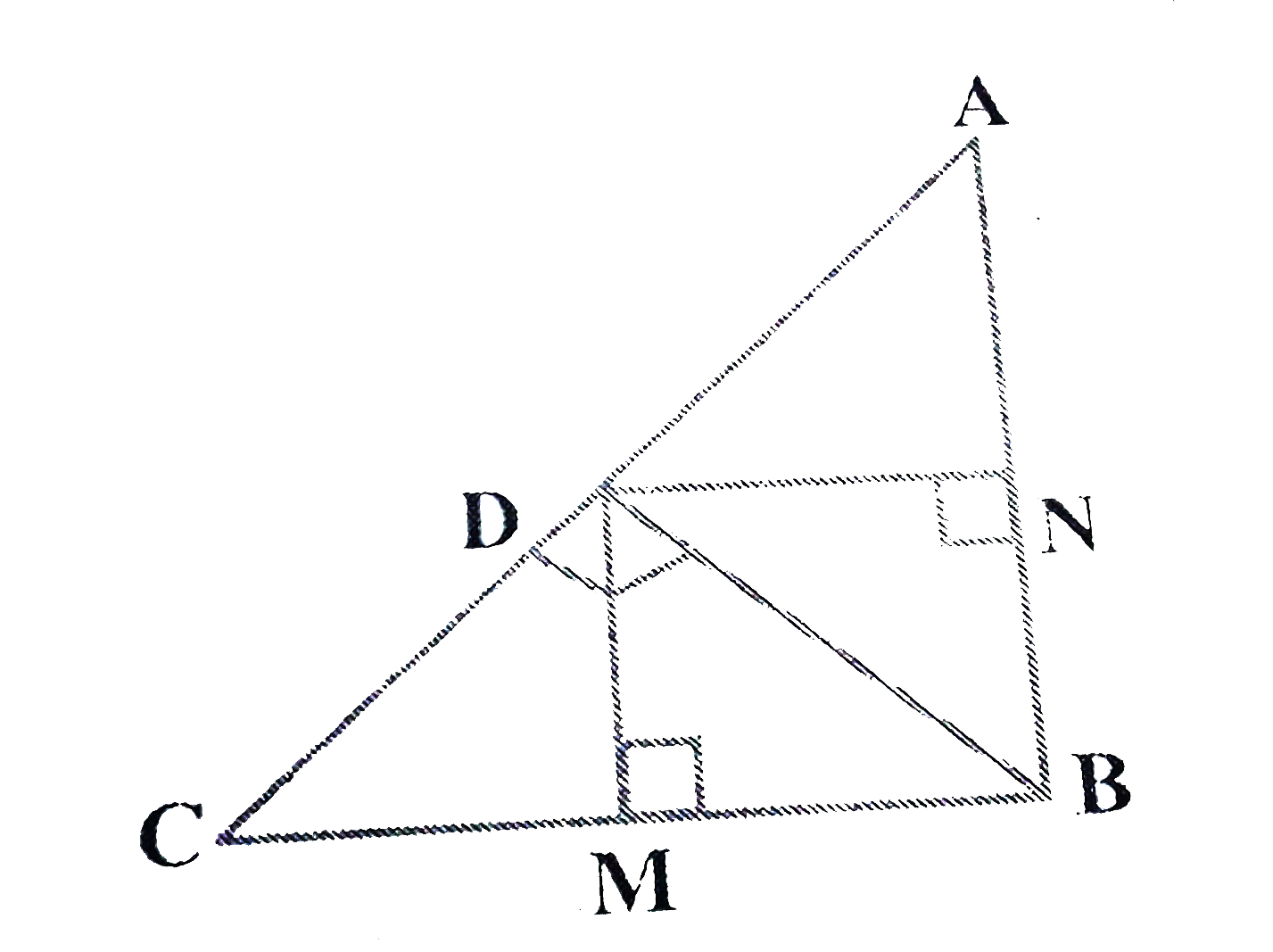
View Solutionआकृति 6.57 में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिंदु है जबकि `BD bot AC ` तथा `DM bot BC ` और `DN bot AB` है । सिद्ध कीजिए कि
(i) `DM^(2)=DN.MC` (ii) `DN^(2)=DM.AN`
View Solutionआकृति 6.68 में ABC एक त्रिभुज हैं जिसमे `angleABC gt 90^(@)` हैं तथा `AD bot CB` हैं| सिध्य कीजिये कि `AC^(2)=AB^(2)+BC^(2)+2BC.BD`

View Solutionआकृति 6.59 में ABC एक त्रिभुज हैं जिसमे `angleABC lt 90^(@)` हैं तथा `AD bot BC` हैं। सिध्य कीजिये कि `AC^(2)=AB^(2)+BC^(2)-2BC.BD` हैं।

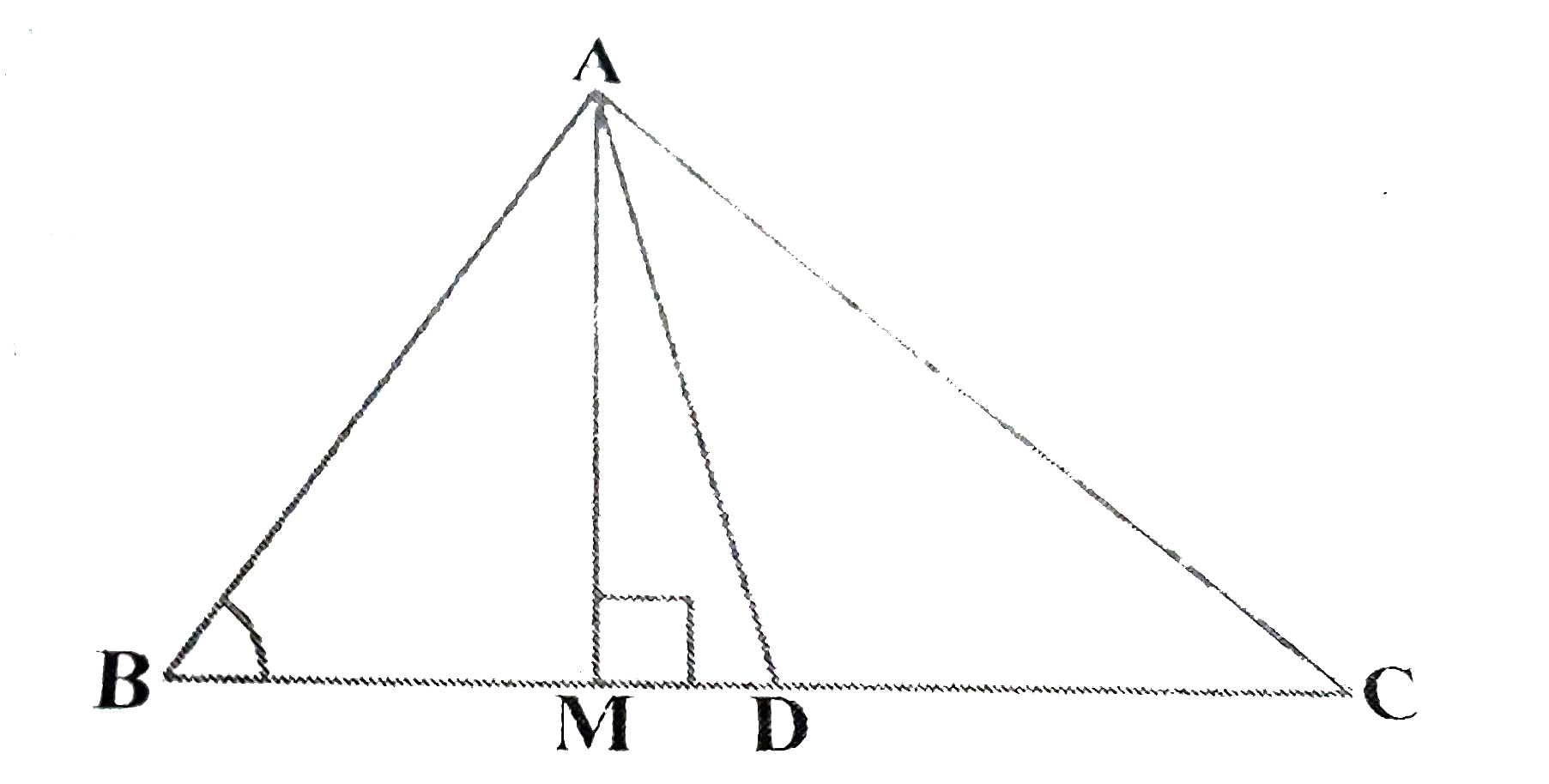
View Solutionआकृति 6.60 में AD त्रिभुज ABC कि एक माधियाका हैं तथा `AM bot BC` हैं। सिध्य कीजिये कि
i) `AC^(2)=AD^(2)+BC.DM + ((BC)/2)^(2)`
ii) `AB^(2)=AD^(2)-BC.DM+((BC)/2)^(2)`
iii) `AC^(2)+AB^(2)=2AD^(2)+1/2BC^(2)`
View Solutionसिद्ध कीजिए कि एक समांतर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है ।
View Solutionएक वृत्त की दो जीवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि:
View Solutionवृत्त की दो जीवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि:
(i) `trianglePAC ~ trianglePDB`
(ii) `PA.PB = PC. PD`
View Solutionआकृति 6.63 में त्रिभुज ABC कि भुजा BC पर एक बिंदु D इस प्रकार स्तिथ हैं कि `(BD)/(CD)=(AB)/(AC)` हैं। स्तिथ कीजिये कि AD, कोण BAC का समद्विभाजक हैं।

View Solutionनाजिमा एक नदी कि धरा में मछलियां पकड़ रही हैं। उसकी मछली पकड़ने वाली छड़ का सिरा पानी का सतह से 1.8 m ऊपर हैं तथा डोरी के निचले सिरे से लगा कांटा पानी के सतह पर स्तिथ बिंदु से उसकी दूरी 2.4 m हैं। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से कांटे तक) तानी हुई हैं, उसने कितनी डोरी बाहर निकली हुई हैं (देखिये आकृति 6.64)? यदि वह डोरी को 5cm/s कि दर से अंदर खींचे, तो 12 सेकंड के बाद नाजिमा कि कांटे से श्रीतीज दूरी कितनी होगी?

View Solution
प्रश्नावली 6.6 (ऐच्छिक) questions and complete solutions for chapter त्रिभुज of DEEPAK PUBLICATION of Class 10