Complete Solutions to UNIT EXERCISE 4 of chapter GEOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | GEOMETRY |
| FULL MARKS | UNIT EXERCISE 4 |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
In the figure, if `BD bot AC and CE bot AB` , prove that
`(i) Delta AEC~ Delta ADB " " (ii) (CA)/(AB)=(CE)/(DB)`

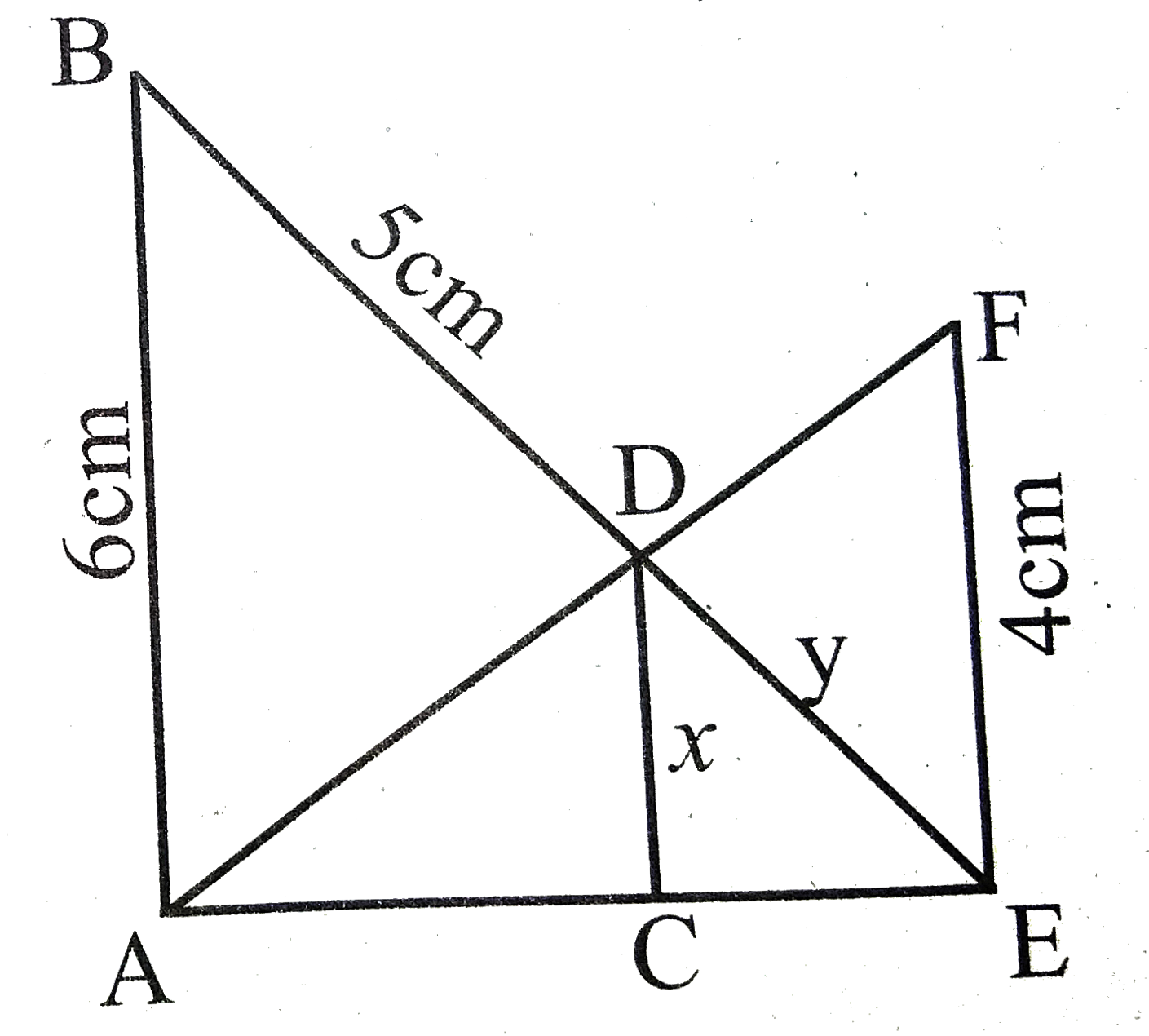
View SolutionIn the given figure, AB||CD ||EF. If AB=6 cm, CD= x cm, EF=4 cm, BD=5 cm and DE=y cm. Find x and y .
View SolutionO is any point inside a triangle ABC. The bisector of `angle AOB, angle BOC and angle COA` meet the sides AB, BC and CA in point D, E and F respectively.
Show that `AD xx BE xx CF= DB xx EC xx FA`
View SolutionIn the figure, ABC is a triangle in which AB= AC. Points D and E are points on the side AB and AC respectively such that AD=AE. Show that points B, C, E and D lie on a same circle.

View SolutionTwo trains leave a railway station at the same time. The first train travels due west and the second train due north . The first train travels at a speed of 20 km/ hr and the second train travels at 30 km/ hr. After 2 hours, what is the distance between them ?
View SolutionD is the mid point of side BC and `AE bot BC`. If BC=a, AC= b, AB=c, ED=x, AD=p and AE=h, prove that
`(i) b^(2)=p^(2)+ax+(a^(2))/(4)`
(ii) `c^(2)=p^(2)-ax+(a^(2))/(4)`
`(iii) b^(2)+c^(2)=2p^(2)+(a^(2))/(2)`
View SolutionA man whose eye-level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4m from the mirror B, he can see the reflection of the top of the tree. How height is the tree ?
View SolutionAn emu which is 8 ft tall standing at the foot of a pillar which is 30 ft height. It walks away from the pillar. The shadow of the emu falls beyond emu. What is the relation between the length of the shadow and the distance from the emu to the pillar ?
View SolutionTwo circles intersect at A and B. From a point P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
View SolutionLet ABC be a triangle and D,E,F are points on the respective sides AB, BC, AC (or their extensions). Let AD : DB=5 : 3, BE : EC= 3 : 2 and AC=21. Find the length of the line segment CF.
View Solution
UNIT EXERCISE 4 questions and complete solutions for chapter GEOMETRY of FULL MARKS MATHS (TAMIL ENGLISH) of Class 10