Two circles intersect at A and B. From a point P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.Solution in Tamil
Step by step video & image solution for Two circles intersect at A and B. From a point P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - FULL MARKSCHAPTER - GEOMETRYEXERCISE - ADDITIONAL QUESTIONS SOLVED (MULTIPLE CHOICE QUESTIONS)
23 Videos
- GEOMETRYBOOK - FULL MARKSCHAPTER - GEOMETRYEXERCISE - ADDITIONAL QUESTIONS SOLVED (ANSWER THE FOLLOWING QUESTIONS)
24 Videos
- GEOMETRYBOOK - FULL MARKSCHAPTER - GEOMETRYEXERCISE - EXERCISE 4.5 (MULTIPLE CHOICE QUESTIONS)
15 Videos
- DEPARTMENTAL MODEL PAPER BOOK - FULL MARKSCHAPTER - DEPARTMENTAL MODEL PAPER EXERCISE - PART-IV
3 Videos
- MENSURATION BOOK - FULL MARKSCHAPTER - MENSURATION EXERCISE - ADDITIONAL QUESTIONS SOLVED (iii)
8 Videos
Similar Questions
If a straight line intersects the sides AB and AC of a △ABC at D and E respectively and is parallel to BC , then AEAC= . ………..
View SolutionThe image of man height 1.8m , is of length 1.5 cm on the film of a camera . If the film is 3 cm from the camera, how far is the man from the camera ?
View SolutionIf in triangles ABC and EDF, ABDE=BCFD then they will be similar, when
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View SolutionA vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View Solutionदो वृत्त दो बिंदुओं B और C पर प्रतिच्छेद करते है । B से जाने वाले तो रेखाखंड ABD और PBQ वृत्तों को A , D और P , Q पर क्रमशः प्रतिच्छेद करते हुए खींचे गए है । सिद्ध कीजिए कि ∠ACP=∠QCD है।

View SolutionThe centre of two circle are P and Q they intersect at the points A and B. The straight line parallel to the line segment PQ through the point A intersects the two circles at the point C and D Prove that CD=2PQ
View SolutionTwo circle intersect each other at A and B and a straight line parallel to AB intersects the circles at C,D,E,F. Prove that CD = EF.
View SolutionTwo circles intersect each other at the points P and Q. A straight line passing through P intersects one circle at A the other circle at .A straight line passing through Q intersect the first circle at C and the second circle at D. Prove that AC∣∣BD.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect on circle at the points A and C and the other circle at B and D . Prove that AC||BD.
View Solutionचित्र में,l और m, एक वृत्त पर बिंदुओं A और B पर दो समानान्तर स्पर्श रेखाएँ हैं। यदि वृत्त पर बिंदु पर खींची गई स्पर्श रेखा , स्पर्श रेखाओं l और m के बीच DE अन्तः खण्ड काटती हैं और F वृत्त का केंद्र हैं ,तो सिद्ध करो कि ∠DEF=90∘
View SolutionTwo circles intersect at A and B. From a point P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
View SolutionTwo circle intersect at two points B and C. Through B, Two lines segment ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively. Prove that ACP=QCD.
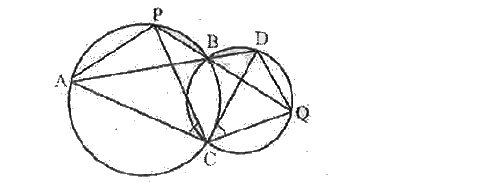
View Solutionகொடுக்கப்பட்ட படத்தில் O மையமாக உடைய வட்டத்தின் ஆரம் 5 செ .மீ ஆகும் .T ஆனது OT =13 செ .மீ என அமைந்த ஒரு புள்ளி மற்றும் OT ஆனது வட்டத்தை E ல் வெட்டுகிறது,வட்டத்தின் E என்ற புள்ளியின் வழியாக செல்லும் ஒரு தொடுகோடு AB எனில் ,AB -யின் நீளம் காண்க ?
View SolutionProve that if the two tangents drawn at the two points on the top of the circle intersect, then the lengths of the two straight lines drawn from the point of intersection to the point of tangent will be equal.
View Solution
