Complete Solutions to EXERCISE 14(C) of chapter EQUATION OF A LINE of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | EQUATION OF A LINE |
| SELINA PUBLICATION | EXERCISE 14(C) |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
Find the equation of a line whose :
y-intercept = 2 and slope = 3.
View SolutionFind the equation of a line whose :
y-intercept = -1 and inclination = `45^@`.
View SolutionFind the equation of the line whose slope is `- 4/3` and which passes through `(-3, 4)`.
View SolutionFind the equation of a line which passes through (5, 4) and makes an angle of `60^@` with the positive direction of the x-axis.
View SolutionFind the equation of the line passing through:
(0, 1) and (1, 2)
View SolutionFind the equation of the line passing through:
(-1, -4) and (3, 0)
View SolutionThe co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively. Find :
the gradient of PQ.
View SolutionThe co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively. Find :
the equation of PQ
View SolutionThe co-ordinates of two points P and Q are (2, 6) and (-3, 5) respectively. Find :
the co-ordinates of the point where PQ intersects the x-axis.
View SolutionThe co-ordinates of two points A and B are (-3, 4) and (2, -1). Find :
the equation of AB.
View SolutionThe co-ordinates of two points A and B are (-3, 4) and (2, -1). Find :
the co-ordinates of the point where the line AB intersects the y-axis.
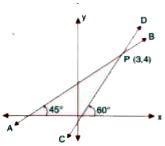
View SolutionThe figure given alongside shows two straight lines AB and CD intersecting each P (3,4) other at point P (3, 4). Find the equations `45^@` of AB and CD.
View SolutionIn `DeltaABC, A = (3,5), B = (7, 8) ` and `C = (1, -10)`. Find the equation of the median through. A.
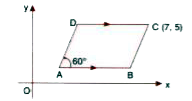
View SolutionThe following figure shows a parallelogram ABCD whose side AB is parallel to the x-axis, `/_A = 60^@` and vertex `C = (7, 5)`. Find the equations of BC and CD.
View SolutionFind the equation of the straight line passing through origin and the point of intersection of the lines `x + 2y = 7` and `x - y = 4` .
View SolutionIn triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (-2, 3) and (0, 1) respectively. Find the equation of median through vertex A.
Also, find the equation of the line through vertex B and parallel to AC.
View SolutionA, B and C have co-ordinates (0, 3), (4, 4) and (8, 0) of triangle ABC respectively. Find the equation of the line through A and perpendicular to BC.
View SolutionFind the equation of the perpendicular dropped from the point (-1, 2) onto the line joining the points (1, 4) and (2, 3).
View SolutionFind the equation of the line, whose :
x-intercept = 5 and y-intercept = 3
View SolutionFind the equation of the line, whose :
x-intercept = -4 and y-intercept = 6
View SolutionFind the equation of the line, whose :
x-intercept = -8 and y-intercept = -4
View SolutionFind the equation of the line whose slope is `-5/6 ` and x-intercept is 6.
View SolutionFind the equation of the line with x-intercept 5 and a point on it (-3, 2).
View SolutionFind the equation of the line through (1, 3) and making an intercept of 5 on the y-axis.
View SolutionFind the equations of the lines passing through point (-2, 0) and equally inclined to the co-ordinate axes.
View SolutionThe line through P(5, 3) intersects y-axis at Q.
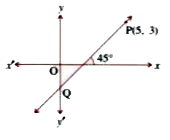
Write the slope of the line.
View SolutionThe line through P(5, 3) intersects y-axis at Q.

Write the equation of the line.
View SolutionThe line through P(5, 3) intersects y-axis at Q.

Find the co-ordinates of Q.
View SolutionWrite down the equation of the line whose gradient is `-2/5 ` and which passes through point P, where P divides the line segment joining A (4, -8) and B (12, 0) in the ratio 3:1.
View Solution`A (1, 4), B (3, 2) and C (7,5)` are vertices of a triangle ABC. Find :
the co-ordinates of the centroid of triangle ABC.
View Solution`A (1, 4), B (3, 2) and C (7,5)` are vertices of a triangle ABC. Find :
the equation of a line, through the centroid and parallel to AB.
View Solution`A (7, -1), B (4, 1) and C (-3, 4) ` are the vertices of a triangle ABC. Find the equation of a line through the vertex B and the point P in AC, such that `AP : CP = 2 : 3`.
View Solution
EXERCISE 14(C) questions and complete solutions for chapter EQUATION OF A LINE of SELINA MATHS (ENGLISH) of Class 10