Complete Solutions to QUESTIONS of chapter EQUATION OF A LINE of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | EQUATION OF A LINE |
| SELINA PUBLICATION | QUESTIONS |
| Number Of Questions | 36 |
| Academic Year | 2023-24 |
Check, whether point (4, -2) lies on the line represented by equation `3x + 5y = 2` or not?
View SolutionThe straight line represented by equation `x - 3y + 8 = 0 ` passes through (2, 4). Is this true ?
View SolutionThe line, represented by the equation `3x - 8y = 2`, passes through the point (k, 2). Find the value of k.
View SolutionDoes the line `3x = y + 1` bisect the line segment joining A (-2, 3) and B (4, 1)?
View SolutionThe line joining the points `(2,\ 1)` and `(5,\ -8)` is trisected at the points `P` and `Q` . If point `P` lies on the line `2x-y+k=0` . Find the value of `k` .
View SolutionFind the slope of the line segment whose inclination is :
`60^@`
View SolutionFind the slope of the line segment whose inclination is :
`52^@`
View SolutionFind the inclination of the line whose slope is:
1
View SolutionFind the inclination of the line whose slope is:
2.9042
View SolutionFind the slope of the line passing through the points A (-2, 3) and B (2,7). Also find the inclination of the line AB.
View SolutionFind the slope of the line passing through the points A (-2, 3) and B (2,7). Also find the inclination of the line AB.
View SolutionFind the slope of the line passing through the points A (-2, 3) and B (2,7). Also find the inclination of the line AB.
View SolutionThe line joining A (-3, 4) and B (2, -1) is parallel to the line joining C (1, -2) and D (0, x). Find x.
View SolutionGiven the points A (2, 3), B (-5, O) and C (-2, a) are collinear. Find 'a'.
View SolutionFind the equation of a line :
whose inclination is `45^@` and y-intercept is 5.
View SolutionFind the equation of a line :
with inclination = `60^@` and passing through (-2, 5).
View SolutionFind the equation of a line :
passing through the points (-3, 1) and (1,5).
View SolutionFind the equation of the line whose x-intercept is 8 and y-intercept is -12.
View SolutionFind the equation of the line whose slope is -3 and x-intercept is also -3.
View SolutionFind the equation of the line which passes through (2, 7) and whose y-intercept is 3.
View SolutionThe equation of a line is `3x - 4y + 12 = 0`. It meets the x-axis at point A and the y-axis at point B. Find :
the co-ordinates of points A and B.
View SolutionThe equation of a line is `3x - 4y + 12 = 0`. It meets the x-axis at point A and the y-axis at point B. Find :
the length of intercept AB, cut by the line within the co-ordinate axes.
View SolutionWrite down the equation of the line whose gradient is `3/2` and which passes through P, where P divides the line segment joining `A(-2, 6) and B(3,-4) ` in the ratio 2 : 3.
View SolutionA straight line passes through the point P(3, 2). It meets the x-axis at point A and the y-axis at point B. If `(PA)/(PB) = 2/3 `. find the equation of the line that passes through the point P and is perpendicular to line AB.
View SolutionFind the equations of the lines which pass through the point (-2, 3) and are equally inclined to the co-ordinate axes.
View SolutionFind the slope and y-intercept of the line `2x - 3y - 4 = 0`
View SolutionGiven two straight lines `3x - 2y = 5` and `2x + ky + 7 =0`. Find the value of k for which the given lines are :
parallel to each other.
View SolutionGiven two straight lines `3x - 2y = 5` and `2x + ky + 7 =0`. Find the value of k for which the given lines are :
parallel to each other.
View SolutionFind the equation of the line passing through (2, -1) and parallel to the line `2x - y = 4`.
View SolutionFind the equation of the line which passes through the point (-2, 3) and is perpendicular to the line `2x + 3y + 4 = 0`
View SolutionGiven two points A (-5, 2) and B (1, -4), find :
mid-point of AB.
View SolutionGiven two points A (-5, 2) and B (1, -4), find :
slope of AB.
View SolutionGiven two points A (-5, 2) and B (1, -4), find :
slope of perpendicular to AB
View SolutionGiven two points A (-5, 2) and B (1, -4), find :
equation of the perpendicular bisector of AB.
View SolutionABCD is a rhombus. The co-ordinates of A and Care (3, 6) and (-1, 2) respectively. Find the equation of BD.
View SolutionMatch the equations A, B, C, D and E with the lines `L_1, L_2, L_3, L_4 and L_5`, whose graphs are roughly drawn in the given diagram.
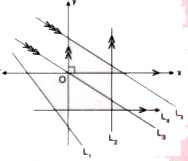
`A -= 2x + y = 0, " " B -= 2x + y = 20 `
`C -= x = 8`,
`D = y = -12 " " E = 2x + 3y + 12 = 0`
View Solution
QUESTIONS questions and complete solutions for chapter EQUATION OF A LINE of SELINA MATHS (ENGLISH) of Class 10