Complete Solutions to EXERCISE 6.3 of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| KUMAR PRAKASHAN | EXERCISE 6.3 |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
State which pairs of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :
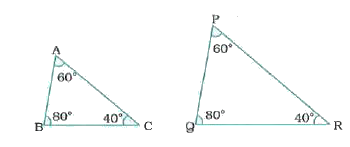
View SolutionState which pairs of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

View SolutionState which pairs of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

View SolutionState which pairs of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :
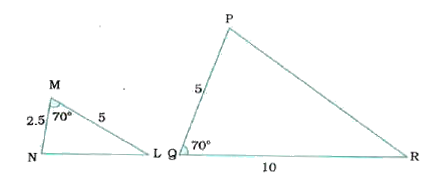
View SolutionState which pairs of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

View SolutionState which pairs of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :
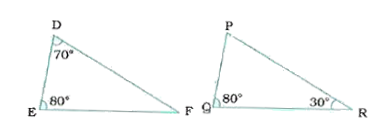
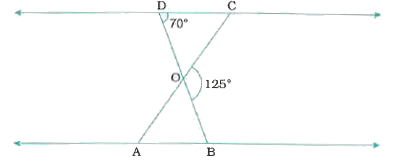
View SolutionIn the given figure `DeltaODC ~ DeltaOBA, /_BOC= 125^(@)" and "/_CDO= 70^(@)`. Find `/_DOC, /_DCO" and "/_OAB`.
View SolutionDigonal AC and BD of a trapezium ABCD with `AB||DC` intersects each other at the point O. Using a similarity criterion for two triangles, show that `(OA)/(OC)=(OB)/(OD)`.
View SolutionIn the given figure `(QR)/(QS)=(QT)/(PR)" and "/_1= /_2`. Show that `DeltaPQS ~ DeltaTQR`.
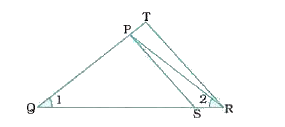
View SolutionS and T are points on sides PR and QR of `DeltaPQR` such that `/_P= /_RTS`. Show that `DeltaRPQ ~ DeltaRTS`.
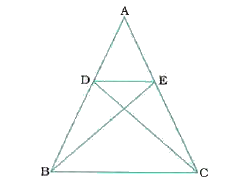
View SolutionIn the given figure, if `DeltaABE cong DeltaACD`, show that `DeltaADE ~ DeltaABC`
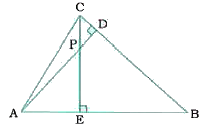
View SolutionIn the given figure, altitudes AD and CE of `DeltaABC` intersect each other at the point P. Show that :
`DeltaAEP ~ DeltaCDP`
View SolutionIn the given figure, altitudes AD and CE of `DeltaABC` intersect each other at the point P. Show that :
`DeltaABD ~ DeltaCBE`

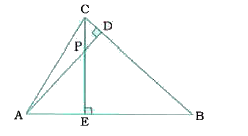
View SolutionIn the given figure, altitudes AD and CE of `DeltaABC` intersect each other at the point P. Show that :
`DeltaAEP ~ DeltaADB`
View SolutionIn the given figure, altitudes AD and CE of `DeltaABC` intersect each other at the point P. Show that :
`DeltaPDC ~ DeltaBEC`

View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that `DeltaABE ~ DeltaCFB`.
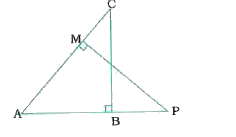
View SolutionIn the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that :
`DeltaABC ~ DeltaAMP`

View SolutionIn the given figure, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that :
`(CA)/(PA)=(BC)/(MP)`
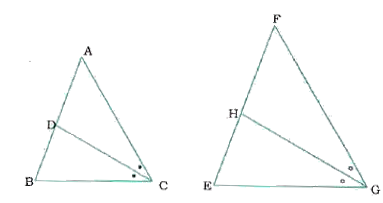
View SolutionCD and GH are respectively the bisectors of `/_ACB" and "/_EGF` such that D and H lie on sides AB and FE of `DeltaABC" and "DeltaEFG` respectively. If `DeltaABC ~ DeltaFEG`, show that :
`(CD)/(GH)=(AC)/(FG)`
View SolutionCD and GH are respectively the bisectors of `/_ACB" and "/_EGF` such that D and H lie on sides AB and FE of `DeltaABC" and "DeltaEFG` respectively. If `DeltaABC ~ DeltaFEG`, show that :
`DeltaDCB ~ DeltaGHE`
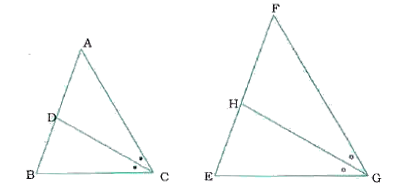
View SolutionCD and GH are respectively the bisectors of `/_ACB" and "/_EGF` such that D and H lie on sides AB and FE of `DeltaABC" and "DeltaEFG` respectively. If `DeltaABC ~ DeltaFEG`, show that :
`DeltaDCA ~ DeltaHGF`

View SolutionIn the given figure, E is a point on side CB produced of an isosceles triangle ABC with AB=AC. If `AD bot BC" and "EF bot AC`, prove that `DeltaABD ~ DeltaECF`
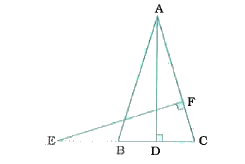
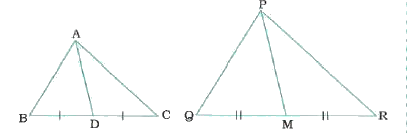
View SolutionSides AB and BC and median AD of a DeltaABC are respectively proportional to sides PQ and QR and median PM of `DeltaPQR` (see the given figure). Show that `DeltaABC ~ DeltaPQR`.
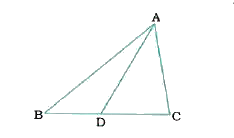
View SolutionD is a point on the side BC of a triangle ABC such that `/_ADC= /_BAC`. Show that `CA^(2)= CB*CD`.
View SolutionSides AB and BC and median AD of a DeltaABC are respectively proportional to sides PQ and QR and median PM of `DeltaPQR` (see the given figure). Show that `DeltaABC ~ DeltaPQR`.

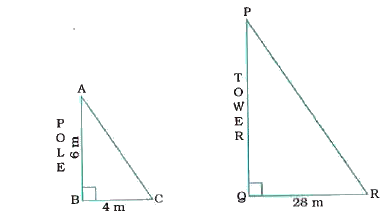
View SolutionA vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
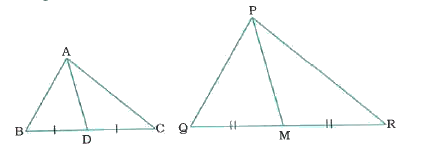
View SolutionIf AD and PM are medians of triangles ABC and PQR respectively , where `DeltaABC ~ DeltaPQR`, prove that `(AB)/(PQ)= (AD)/(PM)`.
View Solution
EXERCISE 6.3 questions and complete solutions for chapter TRIANGLES of KUMAR PRAKASHAN of Class 10