Complete Solutions to OTHER IMPORTANT EXAMPLES of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| KUMAR PRAKASHAN | OTHER IMPORTANT EXAMPLES |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
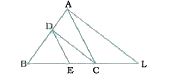
In the given figure, `CD||LA" and "DE||AC`. Find the length of CL if BE= 4 cm and EC= 2 cm.
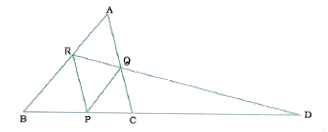
View SolutionIn the given figure, `PQ||BA" and "PR||CA`. If PD= 12 cm, find `BD xx CD`.
View SolutionIn the given figure, `AB||DE" and "BD||EF`. Prove that `DC^(2)= CF xx AC`.
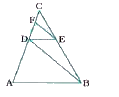
View SolutionABC is a triangle with AB= AC and D is a point on AC such that `BC^(2)= AC xx CD`. Prove that BD= BC.
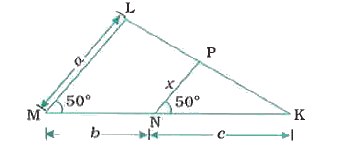
View SolutionIn the given figure, find the value of x in terms of a, b and c.
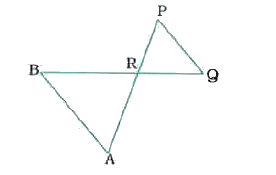
View SolutionIn the given figure, `DeltaABR ~ DeltaPQR`. If PQ= 30 cm, AB= 45 cm, AP= 72 cm and QR= 42 cm, find PR, AR and BR.
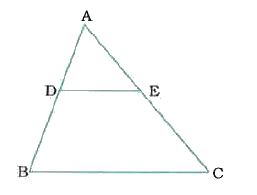
View SolutionIn the given figure, `DE||BC`. If `DE : BC = 3 : 5`, find `(ar(ADE))/(ar(BCED))`.
View SolutionThe areas of two similar triangles are `121 cm^(2)` and `64 cm^(2)` respectively. If the median of the first triangle is`12.1 cm`, find the corresponding median of the second triangle.
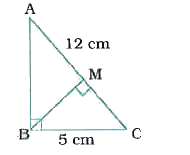
View SolutionIn `DeltaABC, /_B= 90^(@), BM bot AC`, BC= 5 cm and AC = 12 cm. Find the ratio of areas of `DeltaBMC" and "DeltaABC`.
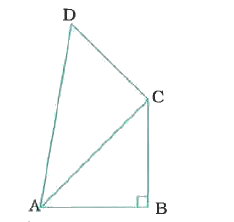
View SolutionIn a quadrilateral ABCD, `/_B= 90^(@)" and "AD^(2)= AB^(2)+BC^(2)+CD^(2)`. Prove that `/_ACD= 90^(@)`.
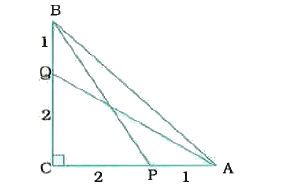
View SolutionIn a right trianlge ABC right angled at C, P and Q are the points on the sides CA and CB respectively which divide these sides in the ratio 2 : 1. Prove that `9(AQ^(2)+BP^(2))= 13AB^(2)`.
View SolutionIn `triangleABC`, AD, BE, CF are the medians. Prove that, `4(AD^(2)+BE^(2)+CF^(2))= 3(AB^(2)+BC^(2)+AC^(2))`.
View Solution
OTHER IMPORTANT EXAMPLES questions and complete solutions for chapter TRIANGLES of KUMAR PRAKASHAN of Class 10