Complete Solutions to Exercise of chapter VOLUME AND SURFACE AREA OF SOLIDS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | VOLUME AND SURFACE AREA OF SOLIDS |
| NAGEEN PRAKASHAN | Exercise |
| Number Of Questions | 68 |
| Academic Year | 2023-24 |
A solid is in the form of a cone standing on a hemisphere with both their radii being equal to 8 cm and the height of cone is equal to its radius . Find the volume of solid.
View SolutionThe following figure shows a model of rocket consisting of a cylinder surmounted by a cone at one end . The dimensions of the model are radius = 3 cm and height of the cone =4 cm and total height =14 cm. Find the (i) total surface area of the model in `pi m^(2)` (ii) the total volume of model in `pi m^(3)`.

View SolutionTwo cubes with each side 10 cm are joined are joined end to end . Find the total surface area of the resulting cuboid.
View SolutionThree equal cubes are placed adjacently in a row. Find the ratio of the total surface area of the resulting cuboid to that of the sum of the total surface areas of the three cubes.
View SolutionFour identical cubes are joined end to end to form a cuboid .If the total surface area of the resulting cuboid is 648 `cm^(2)` .Find the length of edge of each cube.
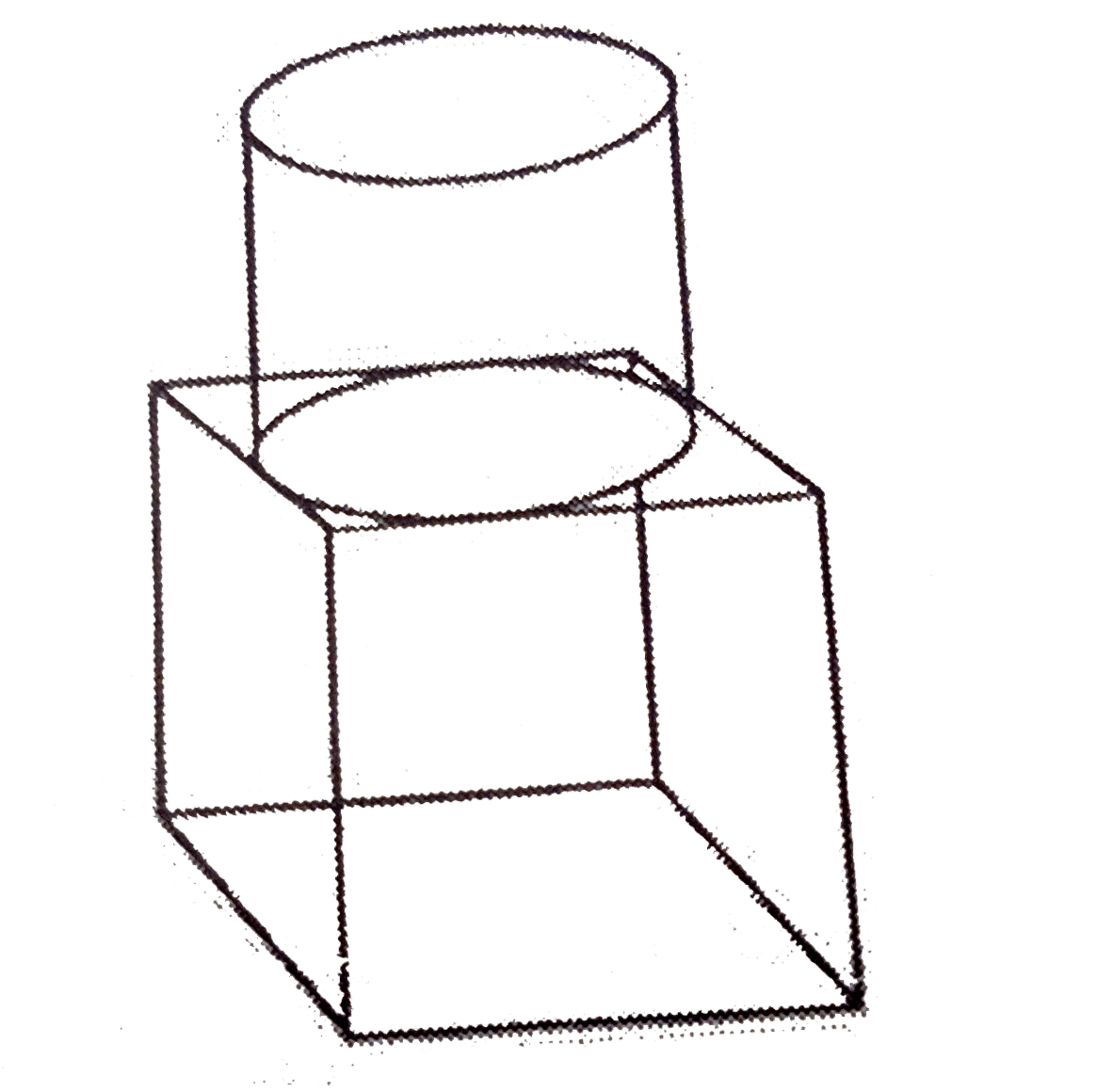
View SolutionThe given figure showns a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown .Find the volume and the total surface area of the whole solid (Take `pi`=3.14)`
View SolutionA circus tent is in the form of a right circular cylinder and right circular cone above it . The diameter and the height of the cylindrical part of the tent are 126 m and 5 m respectively.The totla height of the tent is 21 m. Find the total cost of the tent if the canvas used costsRs 12 per square metre.
View SolutionAn exhibition tent is in the form of a cylinder surmounted by a ocne .The height of the tent above the gournd is 85 cm and the height of the cylindrical part is 50 m. If the diameter of the base is 168 m , find the quantity of canvas required to make the tent . Allow 20% extra for folds and stitching .Give your answer to the nearest `m^(2)`.
View SolutionA pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are `15 cm xx 10 cm xx3.5 cm`.The radius of each of the depression is 0.5 cm and the depht is 1.4 cm .Find the volume of the wood in the entire stand correct to 2 decimal places.
View SolutionA solid consisting of a right circular cone standing on a hemisphere is placed upright in a right circular cylinder full of water and touches the bottom .Find the volume of the water left in the cylinder having given that the radius of the cylinder is 3 cm and its height is 6 cm .The radius of the hemisphere is 2cm and height of the cone is 4 cm. Give your answer to the nearest cubic centimetre.
View SolutionAn iron pillar has some part in the form of a right circular cylinder and remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cubic cm of iron weighs 7.8 grams.
View SolutionA solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
View SolutionA right cylinder , a right cone and a hemishpere have the same height and the same base area .Find the ratio of their (i) volumes
View SolutionFrom a circular cylinder of diameter 10 cm and height 12 cm a conical cavity of the same base radius and of the same height in hollowed out. Find the volume and the whole surfce of the remianing solid .Leave the answer in `pi`.
View SolutionThe height of a solid cylindr is 15 cm and diameter is 7 cm .Two equal conical holes of radius 3 cm and height 4 cm are cut off . Find the volume and surface area of the solid.
View SolutionFind the volume of the largest curcular cone that can be cut out from a cube whose edge is 9 cm.
View SolutionFrom a rectangular solid of metal `42 cm xxx 30 cm xx20 cm` a conical cavity of diameter 14 cm and depth 24 cm is drilled out. Find:
(i) the surface area of remaining solid
(ii) the volume of remaining solid
(iii) the weight of the material drilled out if it weighs `7 gm//cm^(3)`
View SolutionA wooden toy is in the shape of a cone mounted on a cylinder as shown alongside If the height of the cone is 24 cm the total height of the toy is 60 cm and the radius of the base of the cone= twice the radius of the base of the cylinder = 10 cm .Find the total surface area of the you.

View SolutionA sphere just fits in a cylindrical vessel and the height of the cylindrical vessel is the same as the height of the spere . Show that the curved surface area of the cylinder is the same as the curved surface area of the sphere .
View SolutionA room in the form of a cylinder surmounted by a hemisphere valuted dome contains 17.7 `m^(3)` .After recycling, this water is used to irriegate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irrigting the park write you views on recycling of water.
View SolutionIn a hospital used water is collected in a cylindrical tank of diameter 2 m and hight 5 m.After recycling this water is used to irrigate a park of hospital whose length is 25 m and breadth is 20 m. If tank is filled completely then what will be the height of standing water used for irigating the park write your views on recycling of water.
View SolutionThree metal cubes with edges 6cm , 8cm and 10cm respectively are melted together and formed in to a single cube. Find the diagonal of this cube.
View SolutionSix cubes each of side 12 cm are joined end to end .Find the surface area of the cuboid so formed .
View SolutionTwo cubes each of volume 64 `cm^(3)` are joined end to end.Find the surface of the resulting cuboid.
View Solution40 circular plates each of radius 7 cm and thickness 1.5 cm are placed one above the other to form a solid right circular cylindr. Find the total surface area and volume of cylinder so formed.
View SolutionA right circular cone is 8 cm high and radius of its base is 2 cm .The cone is metted and recaset in to a sphere. Determine the diameter of the sphere.
View SolutionA girl fills a cylindrical bucket 32 cm in height and 18 cm in radius with sand .She empties the bucket on the ground and makes a conical heap of the sand .If the height of the conical heap is 24 cm find (i) its radius (ii) its slant height.
View SolutionThe volume of a sphere is `(4pi)/(3) cm^(3)`.Find the volume of that cube whose edge is equal to the diameter of the sphere.
View SolutionA cone of height 4 cm is melted and recast into a sphere of diameter 8 cm .Find the radius of the base of the cone.
View SolutionA metallic sphere of radius 7 cm is melted and recast in to right circular cone of same radius. Find the height of the cone.
View SolutionThe height and base radius of a metallic cone are 216 cm and 16 cm respectively.It melted and recast into a sphere .Find the surface area of the spere.
View SolutionThe base diameter and height of a metallic cone are 24cm and 6cm respectively .It is melted and recast in to a sphere.Find the surface area of the sphere.
View Solution(a) Three metallic spherical balls of radii 3 cm , 4cm and 5 cm are melted and reacast in to a big spherical ball find the radius of this big ball.
(b) Three metallic spheres are melted and recast in to a big solid sphere.Find the radius of big solid sphere if the diameter of three metalic sphres are 16 cm . 12 cm and 2 cm.
View Solution(a) How many balls of radius 1 cm can be drawn by melting metallic sphere of radius 3 cm?
(b) The small spherical balls of diameter 0.6 cm are drawn by melting solid metallic sphere of 3cm radius .Find the number of small balls constructed.
View Solution(a) How many spherical balls of diameter 12 cm can be construct ed by melting a metalic cylinder of diameter 8cm and height 90 cm?
(b) How many spherical balls of diameter 12 cm can be constructed by melting a metallic cylinder of radius 4 cm and height 72 cm.
View SolutionA metallic sphere of radus 4 cm and a metallic cone of base readius 3 cm and height 6 cm are melted and recast a cylinder of 5 cm radus. Find the height of the cylinder.
View SolutionHow many solid speherical balls of radus 3.5 cm can be recast by melting a metallic cone of height 35 cm and base radius 7 cm?
View SolutionThere is some water in a cylindrical vessel of radus 6 cm a sphere of radus 2 cm is dropped in to the vessel .Find the increase in the height of water surface.
View SolutionA solid metallic ball is dropped in a cylindrical vessel which has some waater .when this ball is fully immersed in water the water surface rises by 2 cm find the volume of ball if the radius of base of cylindrical vessel is 7cm.
View Solution(i) The radius of a metallic sphere is 3 cm .It melted and recast in to wire of diameter 0.4 cm Find the length of wire.
(ii) An iron ball oif radius 4 cm is melted .How many small spheres of radus 2 cm can be formed from the material?
View SolutionHow many metallic cones of radius 3 cm and height 13.5 cm are required to construct a metallic sphere of radius 4.5 cm?
View SolutionThe inner radius of a hemispherical cup is 9 cm and it is completely full of water .This water is filled in cylindrical bottles of diameter 3cm and height 4 cm Find the number of bottles required.
View SolutionTwo metallic cones of equal radii 2.1 cm and heights 4.1 cm and 4.3 cm are metled together and recast a sphere. Find the number of sphere so formed.
View SolutionThreee metallic cones of radius 2cm and height 9cm are melted and recast in to a solid sphere. Fuind the radius of the sphere.
View SolutionThreee metallic cones of radius 2cm and height 9 cm are melted and recast in to a solid sphere. Find the radius of the sphere.
View SolutionA metallic cone is melted and recast in to a cylinder of same radius and height 9 cm . Find the height of the cone.
View SolutionA cone of height 15 cm is melted and reacast in to cylinder of same base .Find the height of the cylinder.
View SolutionA cone of same height and same base radius is cut from a cylinder of height 8 cm and base radius 6 cm .Find the total surface area and volume of the remaining solid.
View SolutionThe heights of two cones are same and equal to 6cm .Their radii are 4cm and 3cm .They are melted and recast in to a cylinder of base radius 5cm.Find the height of this cylinder. Volume and surface area of solids
View SolutionFind the volume of a cube whose diagonal is 17.32 metre.
View SolutionThe radius of a spherical ball of iron is 1.5 cm. It is melted and recast into three spherical balls. If the radii of two such balls are 0.75 cm and 1 cm, then find the radius of 3rd ball.
View SolutionWater is being pumped out through a circular pipe whose internal diameter is 7 cm. If the flow of water is 72 cm per second, how many litres of water are being pumped out in one hour?
View SolutionA hemispherical tank of radius 1.75 m is full of water. It is connected with a pipe which empties it at the rate of 7 litres per second. How much time will it take to empty the tank completely?
View SolutionThe curved surface of a cylinder is 100 sq cm .A wire of diameter 5mm is wound round it so as to cover it completely .Find the length of the wire.
View SolutionHow many square metres of canvas will be required to make a conical tent 3 metre high so that a man 2 metre high may stand anywhre with in a radius opf 70 cm from the centre without stoping? Give hyour answwer to the nearest whole number.
View SolutionA rectangular sheet of tin 58 `cmxx44cm` is to be made into an open box by cutting off equal squares from the corners and folding up the flaps.What should be the volume of box if the surface area of box is 2452 `cm^(2)`?
View SolutionA solid metallic right circular cone of height 30cm and radius of the base 12 cm is melted and two solid spheres formed from it. If the volume of one of the sphere is 8 times that of the other find the radius of the smaller sphere.
View SolutionOne cubic metre of a certain metal weighing 900 Kg is melted and then rolled in to a bar whose cross section is a squre and whose length is 9 meter .An exact cube is cut off from it . Find the weight oif this cube.
View SolutionA cone made of paper has height 3h and vertical angle `2 alpha` It contains two other cones of height 2h and h and vertical angles `4 alpha` and `6 alpha` respectively. Find the ratio of the two volumes in between the cones.
View SolutionA solid metal sphere is melted and smaller spheres of equal radii are formed. 10% of volume of the sphere is lost in the process. The smaller spheres have a radius that is `(1/9)th` the larger sphere .If 10 liter of paint were needed to paint the larger sphere .Find how many litres are needed to pausing all the smaller spheres.
View SolutionThe radius of the ends of a bucket of height 24 cm are 15 cm and 5 cm. Find its capacity .Also find the surface area of the buket .
View SolutionThe radii of the ends of a frustum of a cone 45 cm high are 28 cm and 7 cm. Find its volume, the curved surface area and the total surface area.
View SolutionA buket is made of chart paper in the form of cone open at both ends. The radii of its ends are 16 cm and 24 cm and its height is 6 cm .Find the cost of the paper used if one square metre of paper costsRs 0.70.
View SolutionA wooden right circular cone has a bse of radius 3 cm and height 4 cm .The upper part of the cone is cut in such a way that the conical piece will have height 1 cm and base radius 0.75 cm .Find the volume of the remaining porition.
View SolutionThe lower portion of a haystaack is and inverted cone frustum and upper part is a cone as shown in figure .Find the total volume of haystack if AB =3 m and CD=2 m height of cone = 7 m and height of haystack =10.5 m

View SolutionA Hollow cone is cut by a plane parallel to the base and upper portion is removed. If the curved surface of the remainder is 8/9 of the curved surface of the whole cone; find the ration of the line-segment into which the cone's altitude is divided by the plane.
View SolutionA solid metallic right circular cone 20 cm high with vertical angle `60o` is cut into two parts at the middle point of its height by a plane parallel to the base. If the frustum, so obtained, be drawn into a wire of diameter `1/(16)\ c m` , find the length of the wire.
View SolutionThe radius of the base of a right circular cone is r. It is cut by a plane parallel to the base at aheight h from the base. The slant height of the frustum is `sqrt(h^2+4/9r^2)`. Show that the volume of13the frustum is `13/27 pi r^2 h`.
View Solution
Exercise questions and complete solutions for chapter VOLUME AND SURFACE AREA OF SOLIDS of NAGEEN MATHS (HINGLISH) of Class 10