Complete Solutions to Solved Examples of chapter VOLUME AND SURFACE AREA OF SOLIDS of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | VOLUME AND SURFACE AREA OF SOLIDS |
| NAGEEN PRAKASHAN | Solved Examples |
| Number Of Questions | 64 |
| Academic Year | 2023-24 |
A tent of cloth is cylindrical up to 1 m height and conical above it of the same radius of base . If the diameter of tent is 6 m and the slant height of conical part is 5 m, find the cloth required to make this tent
View SolutionA toy is in the form of a cone surmounted by a hemisphere whose radius is `3.5 cm` . If the total height of the toy is `15.5 cm` then find its total surface area and the Volume
View SolutionThe base and top of a right circular cylindrical drum are hemispherical .The diameter of cylindrical part is 14 cm and total height is 30 cm .Find the total surface area of the drum.
View SolutionThere is a hemispherical roof on the cylindrical room .There is 5236 `m^(3)` air in this room .The inner diameter of the floor is equal to the maximum height of the room. Find the height of room . (Given that `pi`=3.1416)
View SolutionThree cubes each with 8 cm edge are joined end to end. Find the total surface area of the resulting cuboid.
View SolutionA rectangular sheet of tin 58 `cmxx44cm` is to be made into an open box by cutting off equal squares from the corners and folding up the flaps.What should be the volume of box if the surface area of box is 2452 `cm^(2)`?
View SolutionThere is some water in a cylindrical vessel of diameter 11 cm .If an iron cube of edge 5.5 cm is entrirely immersed in the water what is the rise in the height of the water in the vessel?
View SolutionThe radii of two right circular cylinders are in the ratio 2: 3 and their heights are in the ratio 5:4 calculate the ratio pof their curved surface areas and also the ratio of their
View SolutionThe dimentsions of a solid iron cuboid are `4.4 m xx 2.6 m xx 1.0 m ` .It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5cm .Find the length of the pipe.
View SolutionIn a rain water harvesting system the rain water form a roof of 22 m `xx` 20m drains in to a cylindrical tank having diameter of base 2m and height 3.5 m . If the tank is full find the rainfall in cm . Write your views on water conservation .
View SolutionVolume and surface area of a solid hemisphere are numerically equal what is the diameter of the hemisphere?
View SolutionThe curved surface are of a cone of height 8 m is 188.4 `m^(2)` .Find the volume of cone
View SolutionA conical tent is required to accommodate 157 persons each person must have 2 m`m^(2)` of space on the ground and 15 `m^(3)` of air to breath .Find the height of the tent , also calculate the slant height.
View SolutionThe radius and height of a solid right circular cone are in the ratio of 5:12 .If its volume is 314 `cm^(3)` Find its total surface area .`[Take pi =3.14]`
View SolutionA right angle triangle with sides 3 cm and 4 cm is revolved around its hypotenuse . Find the volume of the double cone thus generated.
View SolutionIf h,C,V respecitively are the height the curved surface area and volume of a cone prove that `3piVh^(3)-C^(2)h^(2)+9V^(2)=0`
View SolutionA cone of equal height and equal base is cut off from a cylinder of height 24 cm and base radius 7 cm .Find the total surface and volume of remaining solid.
View SolutionFrom a wooden cubical block of edge 7 cm , the largest paossible right conical piece is cut out whose base is on one of the faces of the cube. Calculate .
(i) the volume of the wood left in the block and
the total surface area of the block left (Taken `pi=(22)/(7)`
View SolutionA sphere is inscribed in a cylinder such that spere touches the cylinder . Show that the curved surface of spere is equal to the curved surface of cylinder.
View SolutionThe largest possible cube is made from a wooden sphere of radius `6sqrt(3) cm` . Find the surface area of the cube.
View SolutionThe adjoining figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other end. Given that common radius =3.5 cm the height of the cylinder =6.5 cm and the total height =12.8 cm , claculate the volume of the solid correct to the nearest cm.
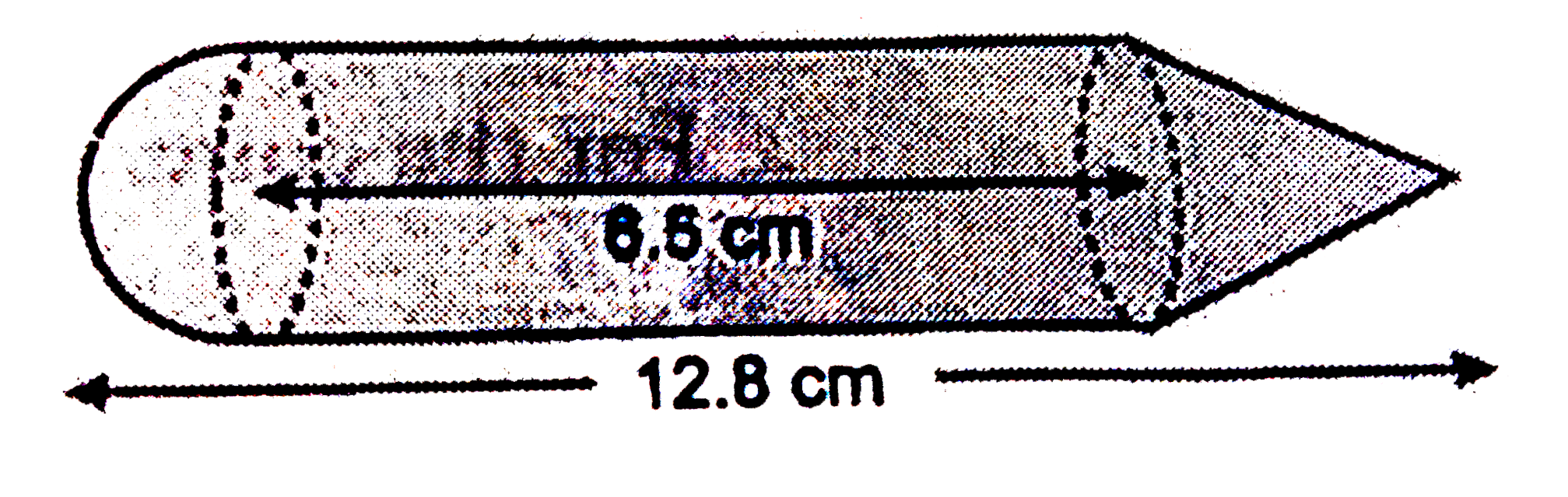
View SolutionFrom a solid cylinder of height 36 cm and radius 14 cm a conical cavity of radus 7 cm and height 24 cm is drilled out . Find the volume and the total surface area of the remaining solid.
View SolutionA hemisphere is inscribed in a cylinder and a cone is inscribed in the hemisphere .The vertex of cone lies on the centre of the upper circular part of the cylinder .Show that , `(1)/(3)xx`Volume of cylinder =`(1)/(2) xx`Volume of hemishphere= Volume of cone
View SolutionA tank measures 2 m long 1.6 m wide and 1m depth water is there up to 0.4 m height .Bricks measuring `25cm xx14cm xx 10 cm` are put in to the tank so that water may come up to the top. Each brick absorbs water equal to `(1)/(7)` th of its own volume
Hopw many bricks will be needed?
View SolutionA solid metal sphere is melted and smaller sperees of equal radii are formed. 10% of the volume of the sphere is lost in the process. The smaller spheres have a radius , that is `(1)/(9)` th the larger sphere . Iof 10 litres of paint were needed to paint the larger sphere. Find how many letres are needed to paint all the smaller spheres?
View SolutionA metallic solid sphere of radius 10.5 is melted and recasted in to smaller solid cones each of radius 3.5 cm and height 3 cm .How many cones will be made?
View SolutionThe three different face diagonals of a cuboid (rectangular parallelopipd ) have lengths 39,40 and 41 units .Find the length of the main diagonal of the cuboid which joins a pair of opposite corners.
View SolutionThree spheres of radius 'r' are kept inside a cuylinder such that two of the speres are at bottom touching each other and sides of the cylinder while the third sphere is touching the two bottom spheres and the top of the cylinder .Find the volume of the cylinder .
View SolutionWater in a canal 5.4 m wide and 1.8 m deep is following with a speed of `25 km//hr` How much area can it irriagae in 40 munutes if 10 cm of standing watr is required for irrigation?
View SolutionA solid metallic cuboid of dimensions `9m xx 8m xx2` is melted and recast in to solid cubes of edge 2 m .find the number of cubes so formed.
View SolutionThree cubes of metal whose edges are in the ratio 3:4:5 are melted down in to a single cube whose diagonal is `12(sqrt(3))` cm. Find the edges of the three cubes.
View SolutionA cube of metal of 2.5 cm edge is melted and cast in to rectangular solid whose base is 1.25 cm by 0.25 cm .Assuming no loss in melting find the height of the solid . Also find the gain in the surface area.
View SolutionA granary is in the shape of a cuboid of size 8m `xx` 6m `xx`3x .If a bag of grain occupies a space of 0.65 `m^(3)` how many bags can be stored in the granary?
View SolutionA cylinderical bucket 28 cm in diameter and 72 cm high is full of water . The water is emptied in to a rectangualr tank 66 cm long and 28 cm wide .Find the height of water level in the tank.
View SolutionA rectangualr container whose base is a square of side 15 cm stands on a horizointal table and holds water up to 3cm from the top .When a cube is placed in the water and is completely submerged , the water rises to the top and 54 `cm^(3)` of water overflows.
Calculate the volume of the cube and its surface area.
View SolutionA solid spherical ball of iron with radius 6 cm is melted and recase tin to three solid spherical balls . The radii of the two of the balls are 3 cm and 4 cm respectively determine the diameter of the third ball.
View Solution50 circular paltes each of radius 7 cm and thickness 0.5 cm are placed one above the other to form a solid right circular cylinder .Find (i) the total surface area and (ii) the volume of the cylinder so formed.
View SolutionA rectangular paper of 22 cm `xx` 12 cm is folded in two different ways and formed two cylinders .
(i) Find the ratio of the volumes of two cylinders
(ii) Find the difference of the volumes of two cylinders.
View SolutionA semicircle of radius 17.5 cm is ratiatied about its diameter. Find the curved surface of so generated solid
View SolutionThe rain water from a roof af dimensions ` 22 m xx 20 m ` drains into a cylindrical vessel having diameter of bases 2 m and height 3.5 m. If the rain water collected form the roof just fill the cylindrica vessl, them find the rainfull (in cm).
View SolutionA sphere of radius 6 cm is melted and reacst in to a cone of height 6 cm .Find the radius of the cone.
View SolutionThe height and radius of base of a metallic cone are 27 cm and 16 cm respectively .It is melted and recast into a sphere .Find the radius and curved surface of the sphere.
View SolutionThere is some water in a cylindrical vessel of diameter 12 cm. A solid metallic spere of redius 4 cm is dropped in to it . Find the increase in height of the water surface if sphere is fully immersed in to the water.
View SolutionThe radius of a metallic sphere is 60 mm .It is melted and recast in to wire of diameter 0.8 mm .Find the length of the wire.
View SolutionA wire of diameter 3mm is wounded around a cylinder whose height is 12 cm and radius 5 cm so as to cover the curved surface of the cylinder completely: find
(i) length of the wire.
(ii) mass of the wire assuming the density of copper to be 8.88 g per `cm^(3)`
View SolutionA metallic cylinder of diameter 16 cm and height 9 cm is melted and recast in to sphere of diameter 6cm .How many such spheres can be formed?
View SolutionA solid metallic right circular cone of height 6.75 cm and radius of the base 12 cm is melted and two solid sphees formed form it. If the volume of one of the sphere is 8 times that of the other find the radius of the smaller sphere.
View SolutionThe radius of a sphericla ball of iron is 1.5 cm .It is melted and recast into three sperical balls .If the radii of two such balls are 0.75 cm and 1 cm , then find the radius of 3rd bal .
View SolutionThe diameter of a hollow cylindrical vessel is 14 cm .There is some water in it. When a cubical iron piece is fully immeresed in it , the water surface rises by `8(9)/(14)`cm .Find the edge of the cube.
View SolutionHow many metallic balls of radius 1 cm can be recast by melting a metallic sphere of radius 8 cm?
View SolutionWater is flowing at the rate of 3km/hr through a circular pipe of 20cm internal diameter into a circular cistern of diameter 10m and depth 2m. In how much time will the cistern be filled?
View SolutionVolume of a sphere is 288 `picm^(3)` .27 small spheres can be formed with this sphee .find the radus of small sphere.
View SolutionA lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interiro .The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm . If length of the pencil is 10 cm, find the voluem of the wood and that of the graphite.
View SolutionFind(i) the lateral or curved surface area of a closed cylindrical petrol storage tank that is4.2 m in diameter and 4.5 m high.(ii) how much steel was actually used, if `1/(12)` of the steel actually used was wasted in making the tank
View SolutionA conical vessel of radius 6 cm and height 8 cm is completely filled with water. a sphere is lowered into the water and its size is such that when it touches the the sides, it just immersed. what fraction of water overflows.
View SolutionA golf ball has diameter equal to 4.1 cm. Its surface has 150 dimples each of radius 2 mm. Calculate totals area which is exposed to the surrounding assuming that the dimples are hemispherical.
View SolutionIn one fortnight of a given month, there was a rainfall of 10cm in a river valley. If the area of the valley is 7280` km^2`. show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
View SolutionA cone is divided in to two parts by drawing a plane through the mid point of its adis parallel to its base. Compare the volume of two parts.
View SolutionThe height of a right circular cone is trisected by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1:7:19.
View SolutionThe radii of the faces of a frustum of a cone are 3 cm and 4 cm and its height is 5 cm find its volumen.
View SolutionThe height of a cone is 30 cm .A small cone is cut off at the top by a plane parallel to the base . If its volume be `(1)/(27)` of the volume of the given cone, at what height above the base the section has been made?
View SolutionThe radii of the ends of a bucket 30 cm high are 21 cm and 7 cm. Find its capacity in litres and the amount of sheet required to make this bucket.
View SolutionA bucket is 32 cm in diameter at the top and 20 cm in diameter at the bottom. Find the capacity of bucket in litres if it is 21 cm deep. Also find the cost of tin sheet used in making the bucket at the rate of Rs 1.50 per sq dm.
View SolutionFind the volume and whole surface of frustum of a square pyramid , thje sides of whose base and top are 24 cm and 16 cm respectively and each of the edges of the frustum is 20cm.
View Solution
Solved Examples questions and complete solutions for chapter VOLUME AND SURFACE AREA OF SOLIDS of NAGEEN MATHS (HINGLISH) of Class 10