Complete Solutions to Coordinate Geometry of chapter COORDINATE GEOMETRY of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | COORDINATE GEOMETRY |
| NCERT EXEMPLAR | Coordinate Geometry |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
The distance of the point `P(2,3)` from the `X`-axis is
View SolutionThe distance between the points `A(0,6)` and `B(0,-2)` is
View SolutionThe distance of the point `P(-6,8)` from the origin is
View SolutionThe distance between the points `(0,5)` and `(-5,0)` is
View SolutionIf `AOBC` is a rectangle whose three vertices are `A(0,3)`,`O(0,0)` and `B(5,0)`, then find the length of its diagonal.
View SolutionThe perimeter of a triangle with vertices (0,4),(0,0) and (3,0) is
View SolutionThe area of a triangle with vertices A(3,0),B(7,0) and C(8,4) is
View SolutionThe points `(-4,0)`,`(4,0)` and `(0,3)` are the verticess of a
View SolutionThe point which divides the line segment joining the points (7,-6) and (3,4) in ratio ` 1 : 2` internally lies in the
View SolutionThe point which lies on the perpendicular bisector of the line segment joining the points A(-2,-5) and B (2,5) is
View SolutionThe fourth vertex D of a parallelogram `ABCD` whose three vertices are `A(-2,3)`, `B(6,7)` and `C(8,3) `is
View Solutionif A(2,1) cuts line P(2,1) and B(8,4) then
View SolutionIf `P((a)/(3),4)` is the mid - point of the line segment joining the points `Q(-6,5)` and `R(-2,3)`, then the value of `a` is
View SolutionThe perpendicular bisector of the line segment joining the points A(1,5) and B(4,6) cuts the Y-axis at
View SolutionThe coordinates of the point which is equidistant from the three vertices of the `triangle AOB` as shown in the figure is
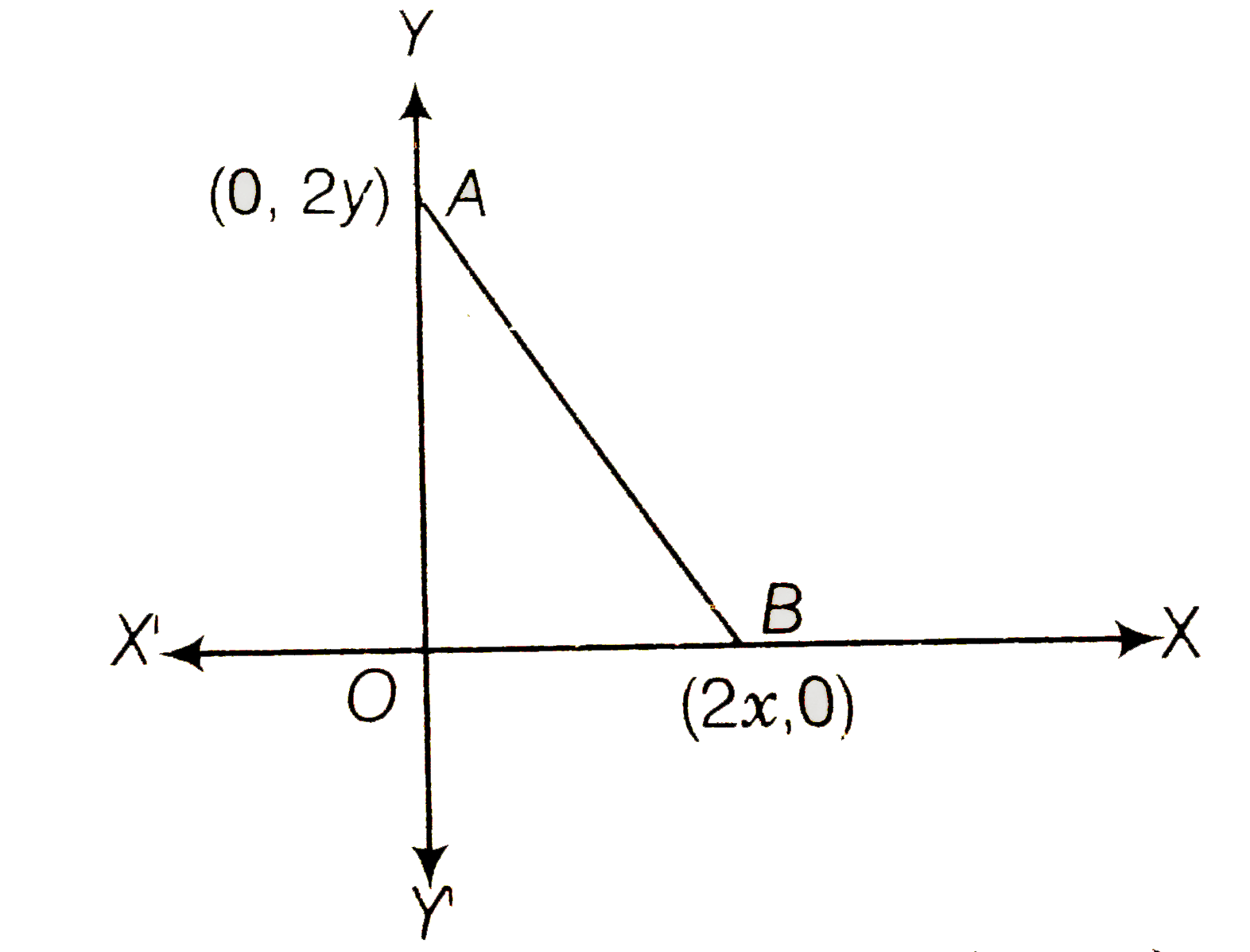
View SolutionIf a circle drawn with origin as the centre passes through `(13/(2),0)`, then the point which does not lie in the interior of the circle is
View SolutionA line intersects the Y- axis and X-axis at the points P and Q, respectively. If (2,-5) is the mid- point of PQ, then the coordinates of P and Q are, respectively.
View SolutionThe area of a triangle with vertices (a,b+c), (b,c+a) and (c,a+b) is
View SolutionIf the distance between the points (4,p) and (1,0) is 5 , then find the value of p.
View SolutionIf the points A(1,2) , B(0,0) and C (a,b) are collinear , then
View Solution`triangle` ABC with vertices A(0-2,0),B(2,0) and C(0,2) is similar to `triangle` DEF with vertices D(-4,0) ,E(4,0) and F(0,4).
View SolutionThe point P(-4,2) lies on the line segment joining the points A(-4,6) and B (-4,-6).
View SolutionThe points (0,5) , (0,-9) and (3,6) are collinear.
View SolutionPoint P(0,2) is the point of intersection of Y-axis and perpendicular bisector of line segment joining the points A(-1,1) and B(3,3).
View SolutionThe points A(3,1) , B (12,-2) and C(0,2) cannot be vertices of a triangle.
View SolutionProve that the points A(4,3), B(6,4), C(5,-6) and D(-3,5) are vertices of a parallelogram.
View SolutionA circle has its centre at the origin and a point P (5,0) lies on it . The point Q (6,8) lies outside the circle.
View SolutionThe point A (2,7) lies on the perpendicular bisector of the line segment joining the points P (5,-3) and Q(0,-4).
View SolutionThe point P (5,-3) is one of the two points of trisection of line segment joining the points A(7,-2) and B(1,-5).
View SolutionThe points A (-6,10), B(-4,6) and C(3,-8) are collinear such that
AB `=-(2)/(9)AC`.
View SolutionThe points P (-2,4) lies on a circle of radius 6 and centre (3,5).
View SolutionThe points A (-1,-2), B (4,3) ,C (2,5) and D (-3,0) in that order form a rectangle.
View SolutionName the type of triangle formed by the points A (-5,6) , B (-4,-2) and C (7,5).
View SolutionFind the points on the X-axis which are at distance of `2sqrt(5)` from the point (7,-4) . How many such points are there ?
View SolutionWhat type of quadrilateral do the points `A (2,-2), B (7,3), C(11,-1) and D (6,-6)` taken in that order form?
View SolutionFind the value of a , if the distance between the points A (-3,-14) and B (a,-5) is 9 units.
View SolutionFind a point which is equidistant from the points A(-5,4) and B (-1,6). How many such points are there ?
View SolutionFind the coordinates of the point Q on the X- axis which lies on the perpendicular bisector of the line segment joining the points A (-5,-2) and B (4,-2). Name the type of triangle formed by the points Q , A and B.
View SolutionFind the value of m, if the points (5,1), (-2,-3) and (8,2m) are collinear.
View SolutionIf the points A(2,-4) is equidistant from P (3,8) and Q (-10,y), then find the value of y . Also , find distance PQ.
View SolutionFind the area of the triangle wohose vertices are (-8,4) ,(-6,6) and (-3,9).
View SolutionIn what ratio does the X -axis divide the line segment joining the points (-4,-6) and (-1,7) ? Find the coordinates of the points of division.
View SolutionFind the ratio in which the point P`((3)/(4),(3)/(12))` divides the line segment joining the points A `((1)/(2),(3)/(2))` and B `(2,-5)`.
View SolutionIf P (9a-2,-b) divides line segment joining A (3a+1,-3) and B(8a,5) in the ratio `3 : 1`, then find the values of a and b.
View SolutionIf (a,b) is the mid - point of the line segment joining the points A (10,-6), B(k,4) and a-2b =18, then find the value of k and the distance AB.
View SolutionIf the centre of a circle is (2a,a-7) ,then Find the value of a , if the circle passes through the point (11,-9) and has diameter `10sqrt(2)` units .
View SolutionThe line segment joining the points A(3,2) and B (5,1) is divided at the point P in the ratio `1 : 2` and it lies on the line `3x-18y+k=0`. Find the value of k.
View SolutionIf D `(-(1)/(2),(5)/(2))`, E (7,3) and F `((7)/(2),(7)/(2))` are the mid - points of sides of `triangle ABC`, then find the area of the `triangleABC`.
View SolutionIf the points A (2,9), B (a,5) and C (5,5) are the vertices of a `triangleABC`. Right-angled at B, then find the values of a and hence the area of `triangleABC`.
View SolutionFind the coordinates of the point R on the line segment joining the points P`(-1,3)` and Q `(2,5)` such that PR `=(3)/(5)` PQ.
View SolutionFind the values of k, if the points A (k+1,2k) ,B (3k,2k+3) and C (5k-1,5k) are collinear.
View SolutionFind the ratio in which the line `2x+3y-5=0` divides the line segment joining the points (8,-9) and (2,1). Also find the coordinates of the points of division.
View SolutionIf (-4,3) and (4,3) are two vertices of an equilateral triangle, then find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
View SolutionA(6,1) , B (8,2) and C (9,4) are three vertices of a parallelogram ABCD . If E is the mid - point of DC , then find the area of `triangle`ADE.
View SolutionThe points A `(x_(1),y_(1)), B (x_(2),y_(2)) and C (x_(3),y_(3))` are the vertices of `triangle`ABC.
(i) The median from A Meets Bc at D. Find the coordinates of the points D.
(ii) Find the coordinates of the point P on Ad such that `AP : PD = 2 : 1`.
(iii) Find the coordinates of points Q and R on medians BE and CF, respectively such that `BQ : QE=2 :1 and CR : RF =2 : 1`.
What are the coordinates of the centroid of the `triangle` ABC?
View SolutionIf the points A (1,-2), B (2,3) , C (a,2) and D (-4-,3) form a parallelogram , them find the value of a and height of the parallelogram taking AB as base.
View SolutionStudents of a school are standing in rows and columns in their playground for a drill practice . A, B, C and D are the positions of four students as shown in figure . Is it possible to place Jaspal inn the drill in such a way that he is equidistant from each of the four students A, B C and D ? If so, what should be his position ?
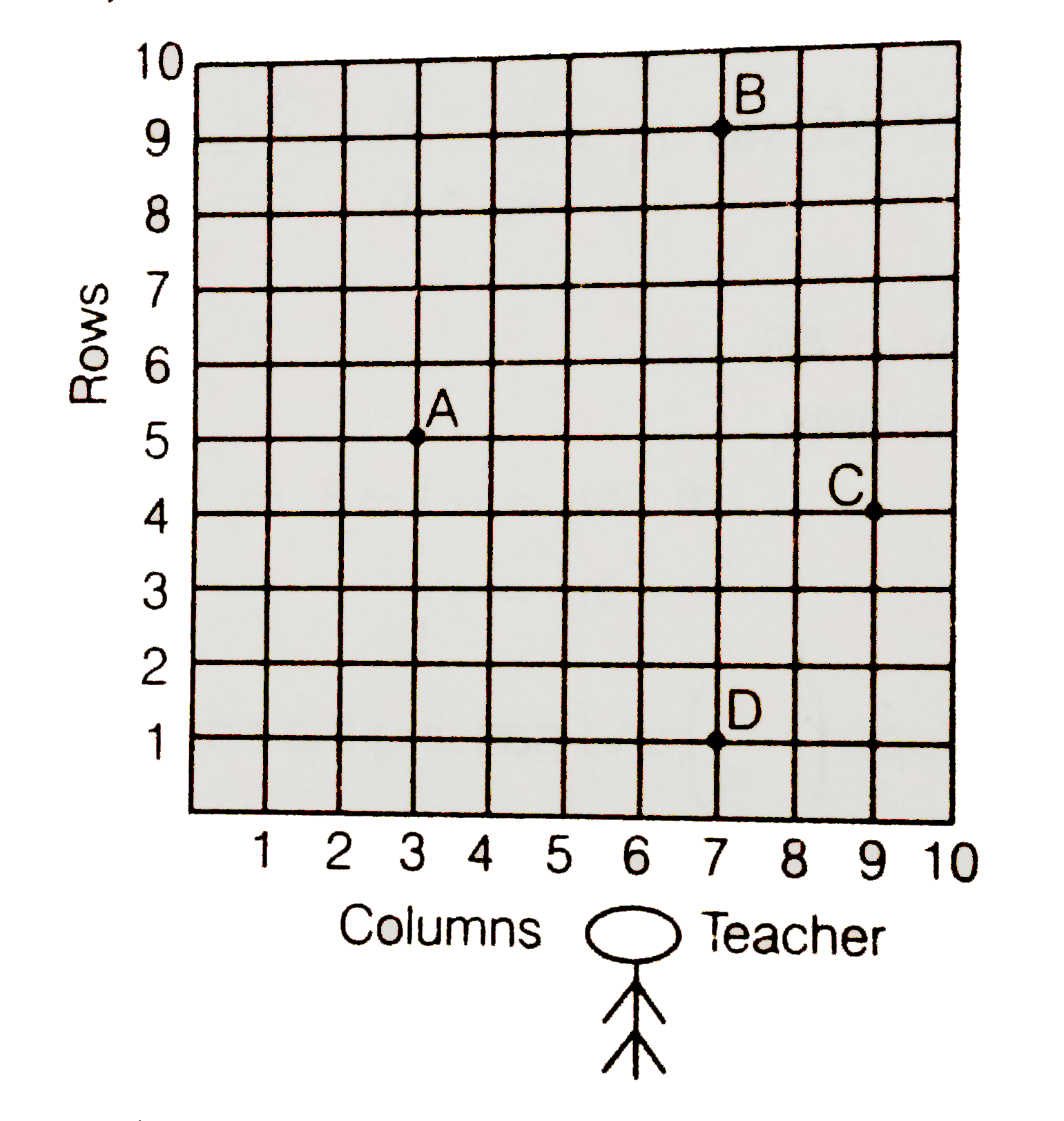
View SolutionAyush starts walking from his house to office . Instead of going to the office directly , he goes to bank first , from there to his daughter 's school and then reaches the office. What is the extra distance travelled by Ayush in reaching his office ? (Assume that all distance covered are in straight lines ). If the house is situated at (2,4) bank at (5,8), school at (13,14) and office at (13,26) and coordinates are in km.
View Solution
Coordinate Geometry questions and complete solutions for chapter COORDINATE GEOMETRY of NCERT EXEMPLAR MATHS (HINGLISH) of Class 10