Complete Solutions to एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.3) of chapter त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | त्रिभुज |
| MADHUR GUPTA | एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.3) |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
बताइये कि आकृति में दिए त्रिभुजों के युग्मो में कोण-कोण से युग्म समरूप है उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप व्यक्त कीजिये
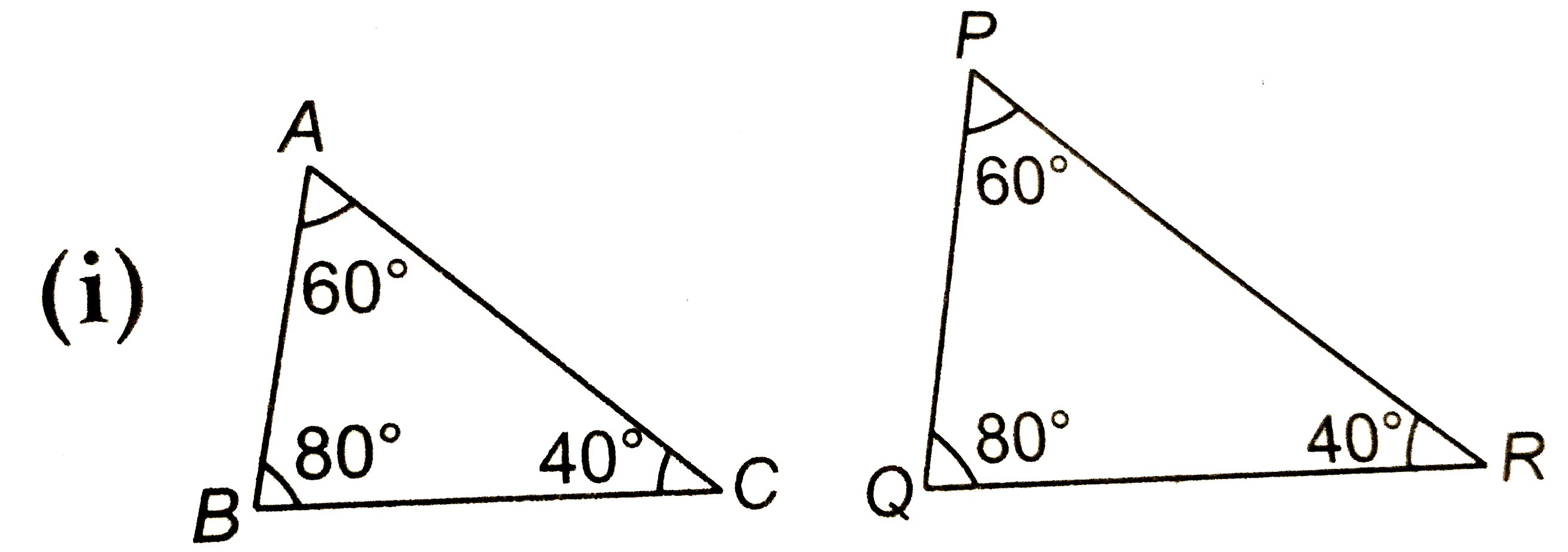
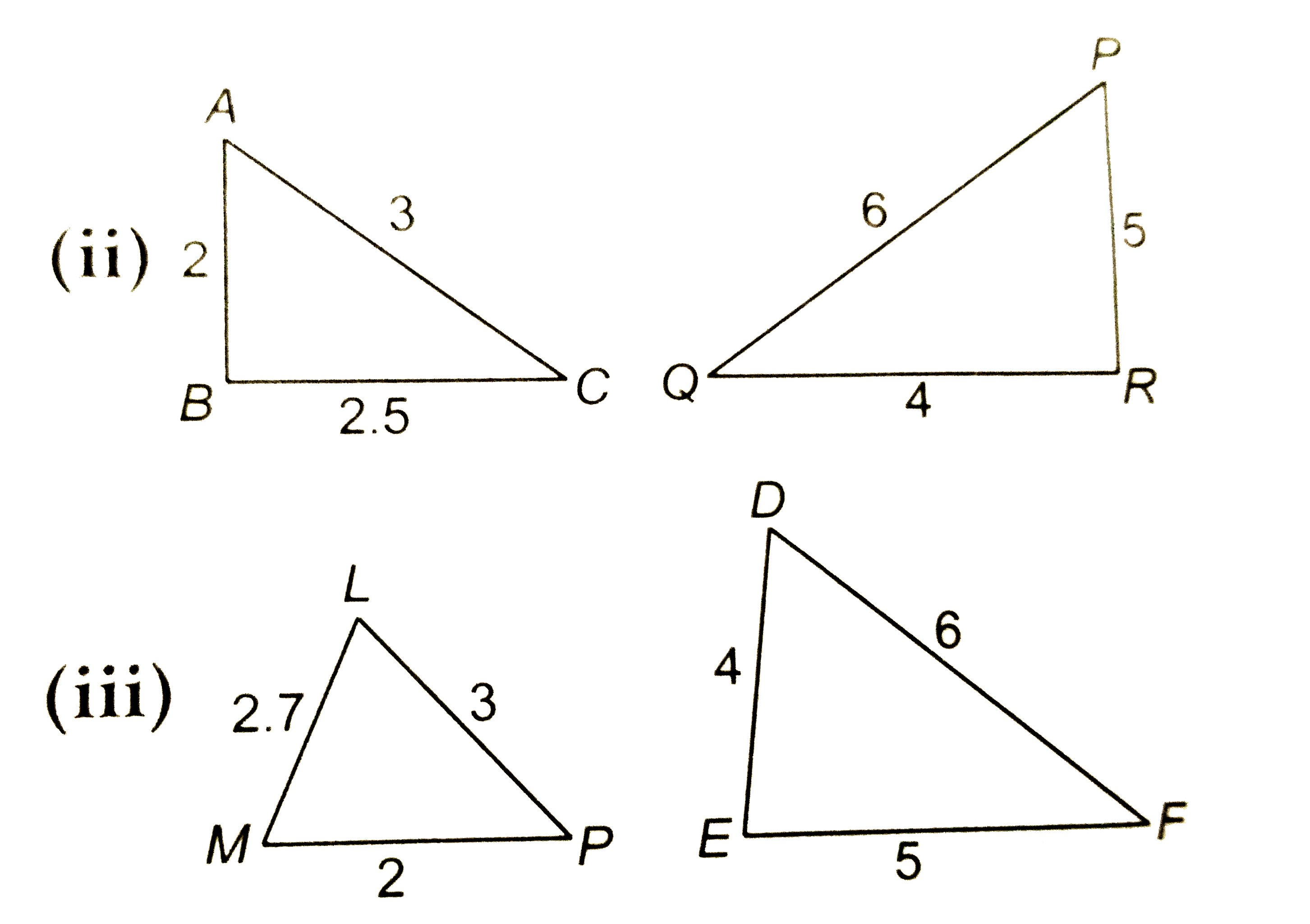
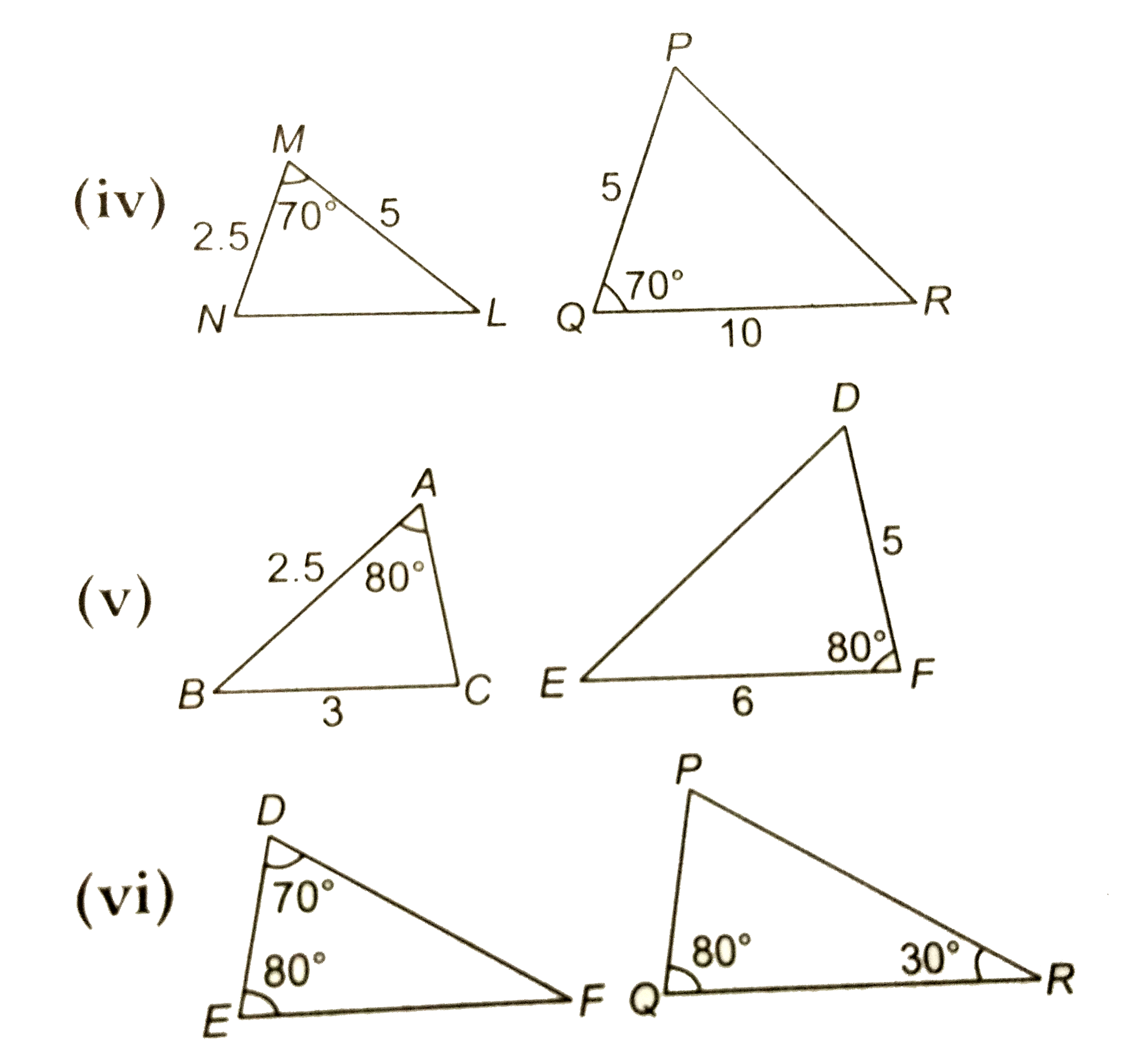
View Solutionआकृति में, `DeltaODC~DeltaOBA, angleBOc=125^@` और `angleCDO=70^@` है `angleDOC,angleDCO` और `angleOAB` ज्ञात कीजिये
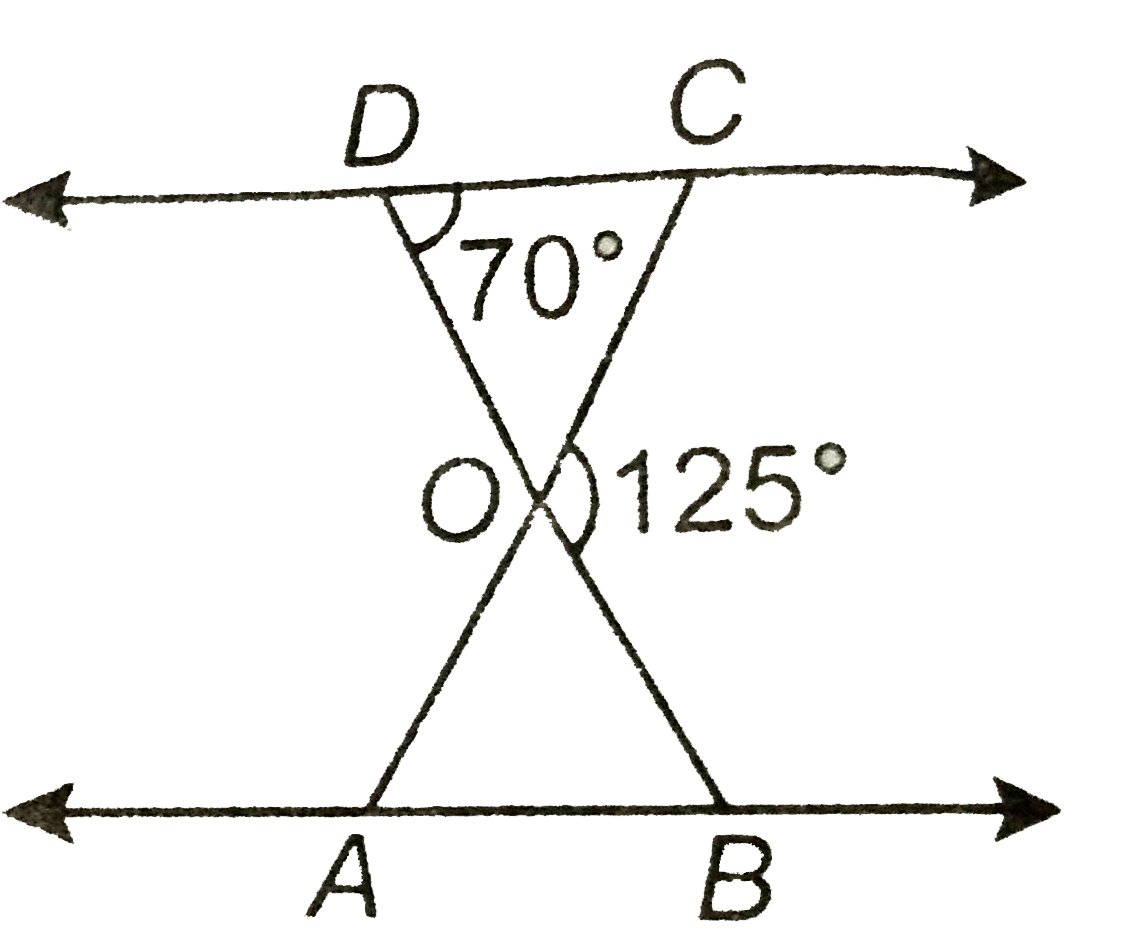
View Solutionसमलम्ब ABCD , जिसमे AB||DC है के AC विकर्ण BD और परस्पर O पर प्रतिच्क्षेद करते है दो त्रिभुजों की समरूपता कसौटी का प्रयोग करते हुए , दर्शाइए कि `(OA)/(OC)=(OB)/(OD)` है
View Solutionआकृति म, `(QR)/(QS)=(QT)/(PR)` तथा `angle1=angle2` है दर्शाइए कि `DeltaPQS~DeltaTOR` है
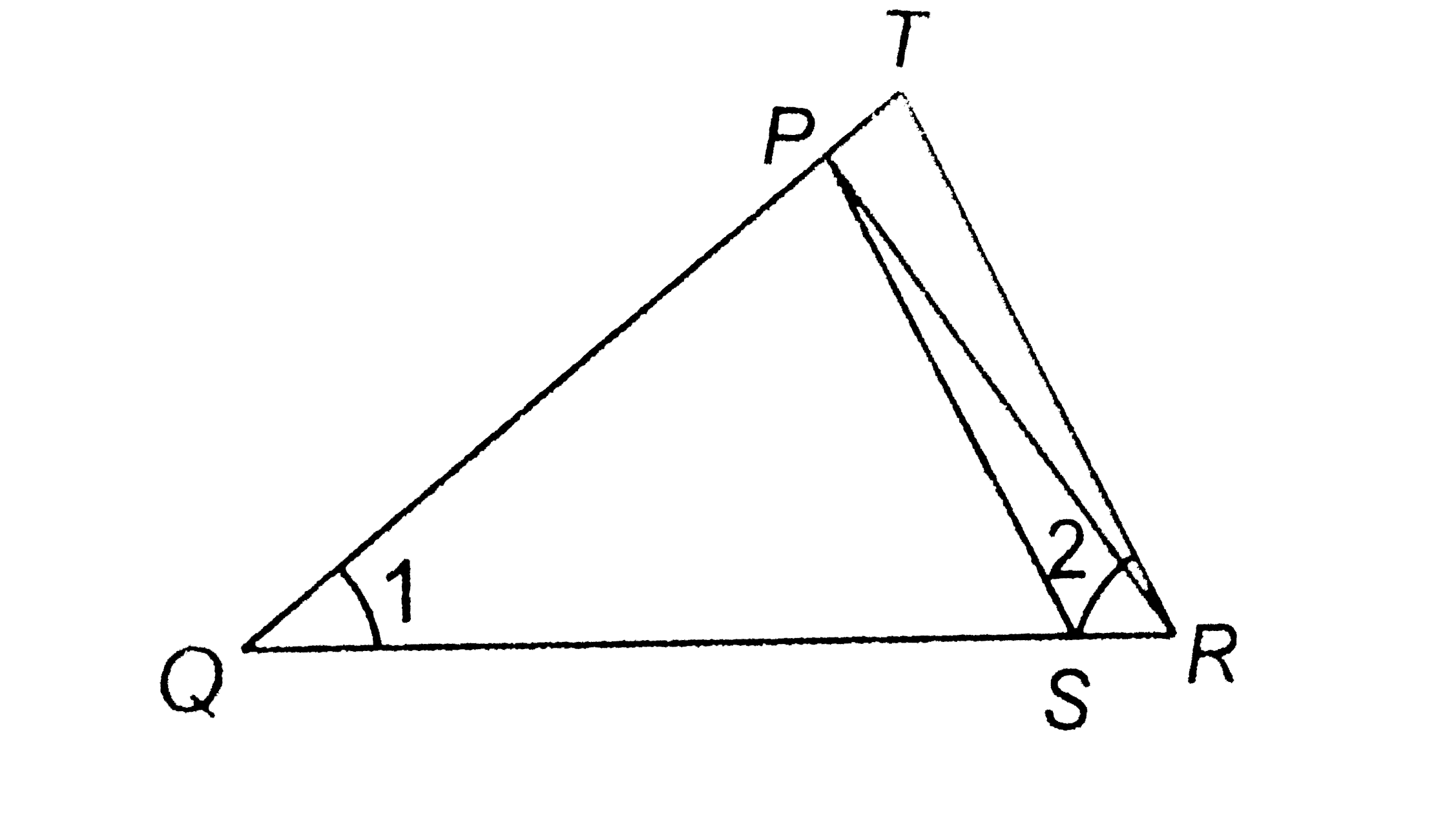
View Solution`DeltaPQR` की भुजाओ PR और QR पर क्रमशः बिन्दु S और T इस प्रकार स्थित है कि `angleP=angleRTS` है दर्शाइए कि `DeltaRPQ~DeltaRTS` है
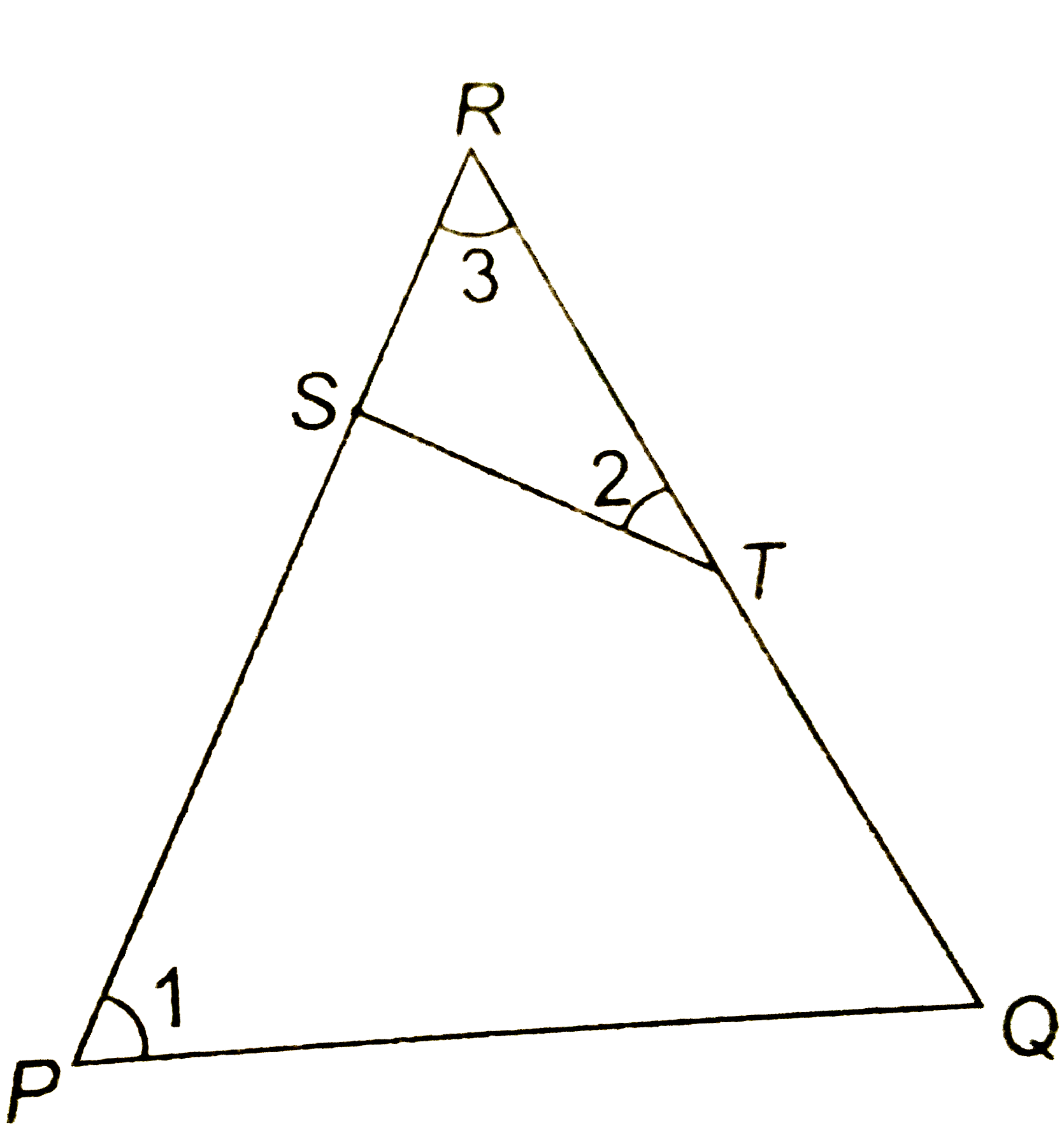
View Solutionआकृति में यदि `DeltaABE~=DeltaACD` है तो दर्शाइए कि `DeltaADE~=DeltaABC` है
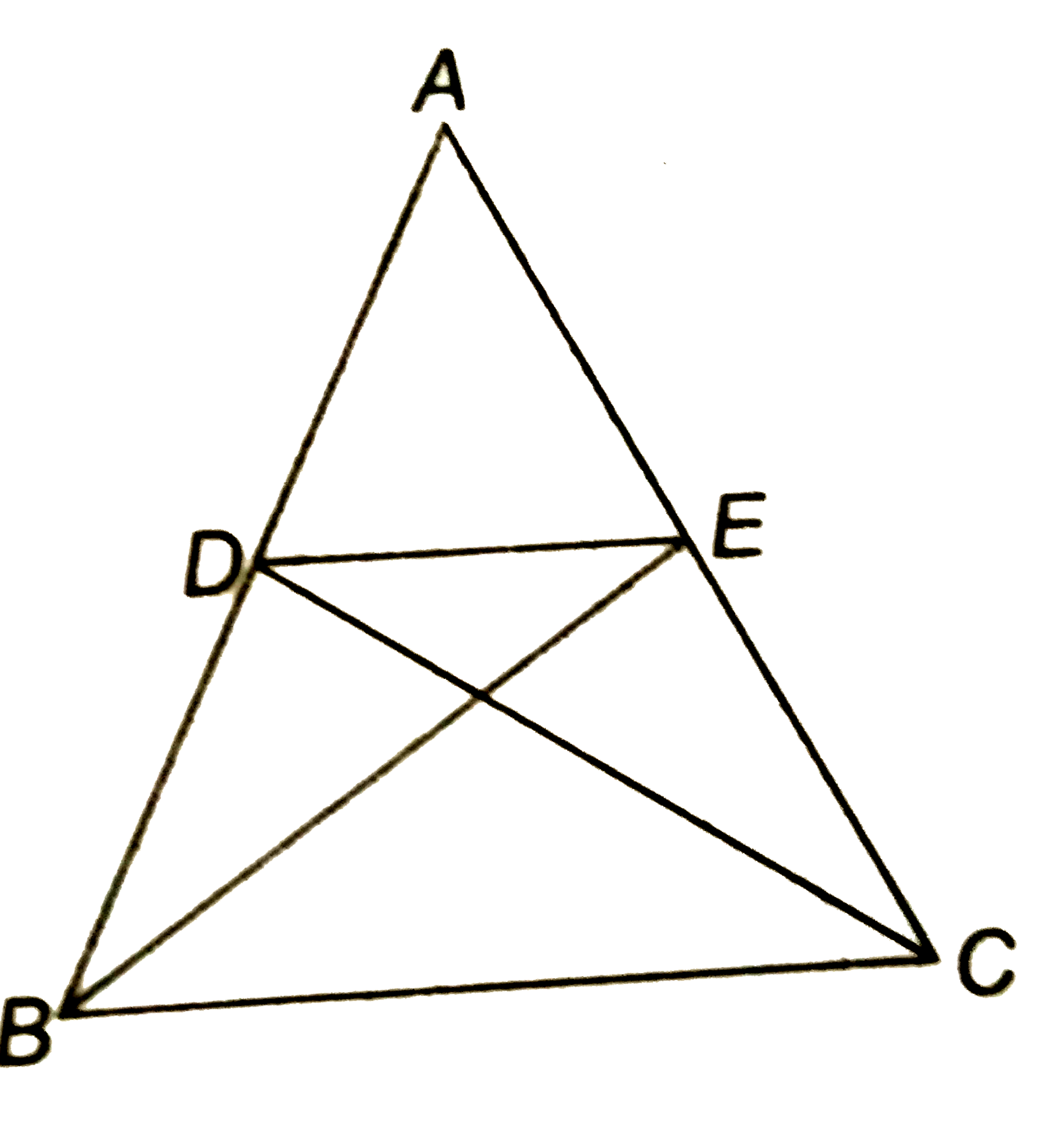
View Solutionआकृति में `DeltaABC` के शीर्षलम्ब AD और CE परस्पर बिन्दु P पर प्रतिच्छेद करते है दर्शाइए कि
(i) `DeltaAEP~DeltaCDP`
(ii) `DeltaABD~DeltaCBE`
(ii) `DeltaAEP~DeltaADB`
`DeltaPDC~DeltaBEC`
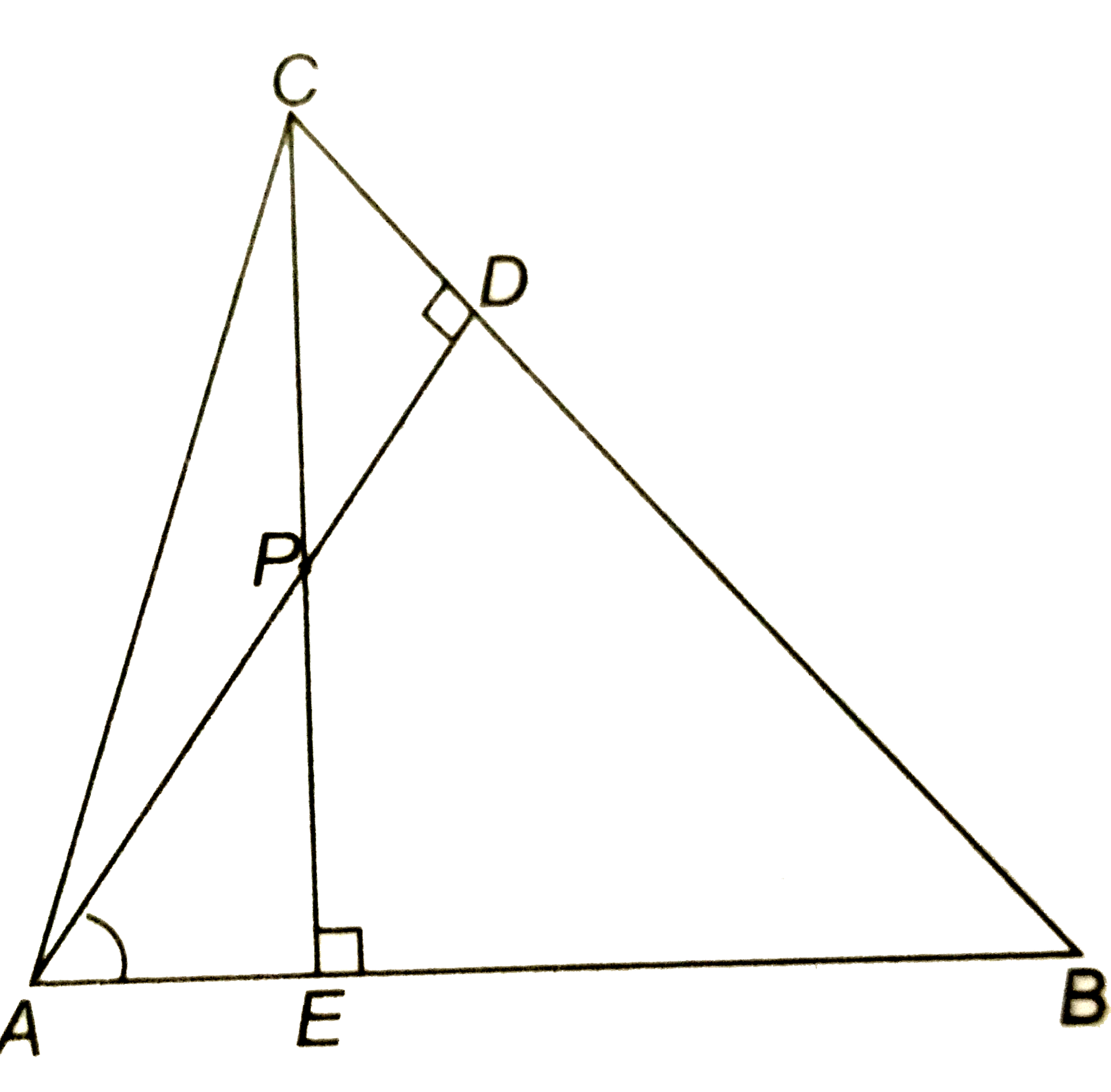
View Solutionसमान्तर चतुर्भुज ABCD कि बढ़ाई गयी भुजा AD पर स्थित E एक विन्दु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है दर्शाइए कि `DeltaABE~DeltaCFB` है
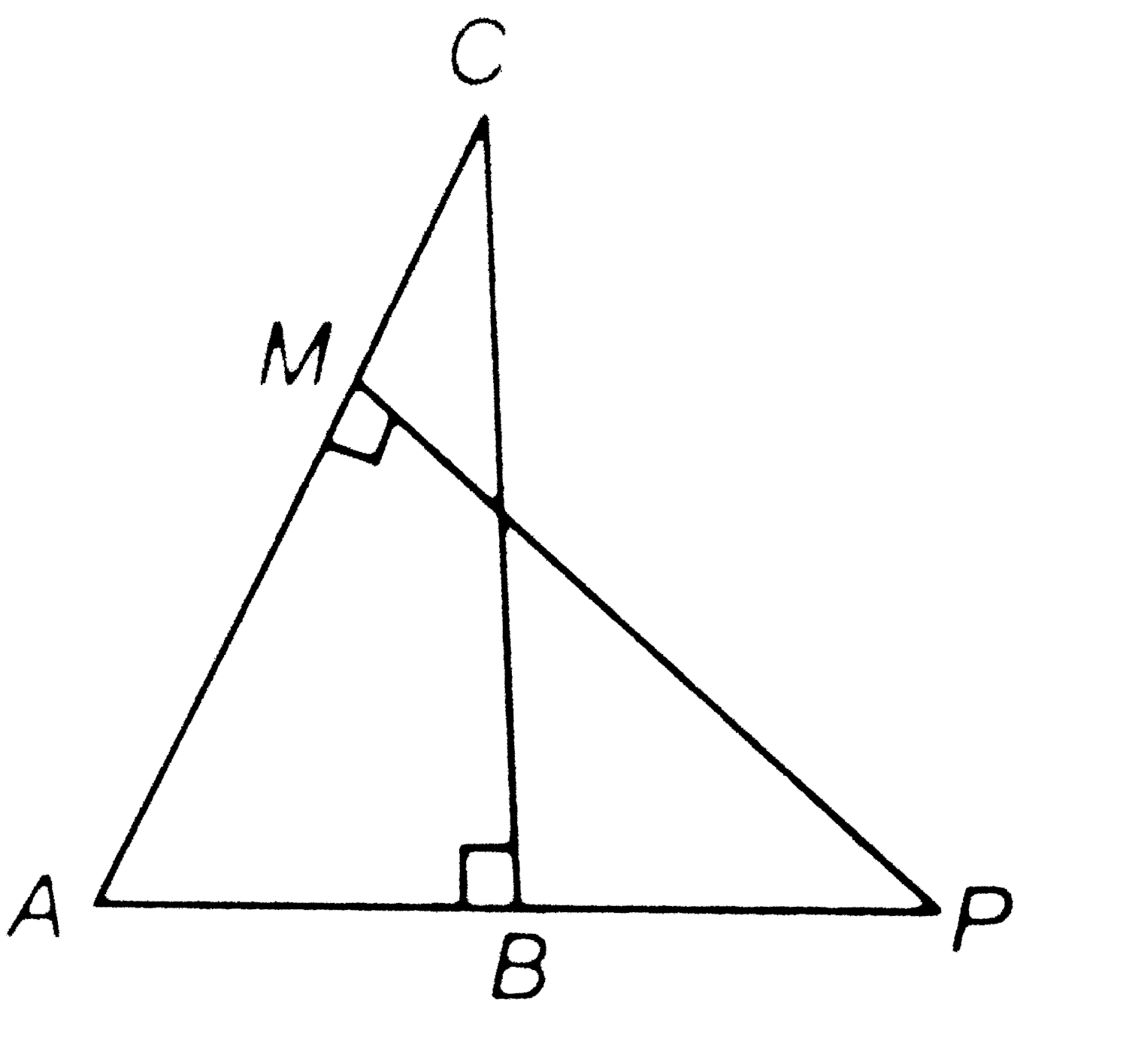
View Solutionआकृति में , ABC और AMP दो समकोण त्रिभुज है जिनके B और M समकोण है सिद्ध कीजिये कि
(i) `DeltaABC~DeltaAMP`
(ii) `(CA)/(PA)=(BC)/(MP)`
View SolutionCD और GH क्रमशः `angleACB" और "angleEGF` के ऐसे समद्विभाजक है कि बिंदु D और H क्रमशः `DeltaABC` और `DeltaFEG` की भुजाओ AB और FE पर स्थित है यदि `DeltaABC~DEltaFEG` है तो दर्शाइए कि
(i) `(CD)/(GH)=(AC)/(FG)`
(ii) `DeltaDCB~DeltaHGF`
(iii) `DeltaDCA~DeltaHGF`
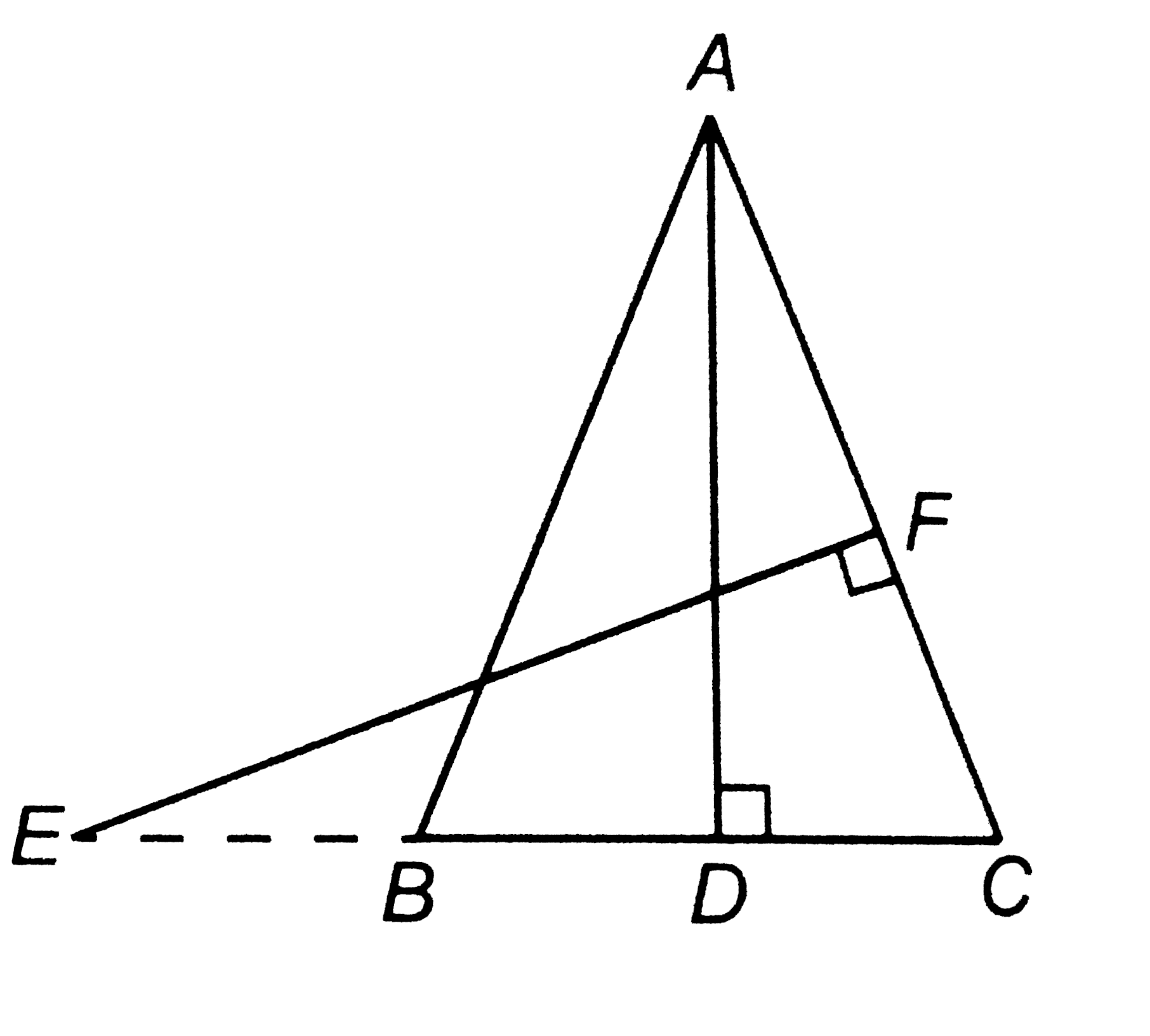
View Solutionआकृति में AB = AC वाले , एक समद्विबाहु त्रिभुज ABC कि बढ़ाई गयी भुजा CB पर स्थित E बिंदु है यदि `ADbotBC" और "EFbotAC` है तो सिद्ध कीजिये कि `DeltaABD~DeltaECF` है
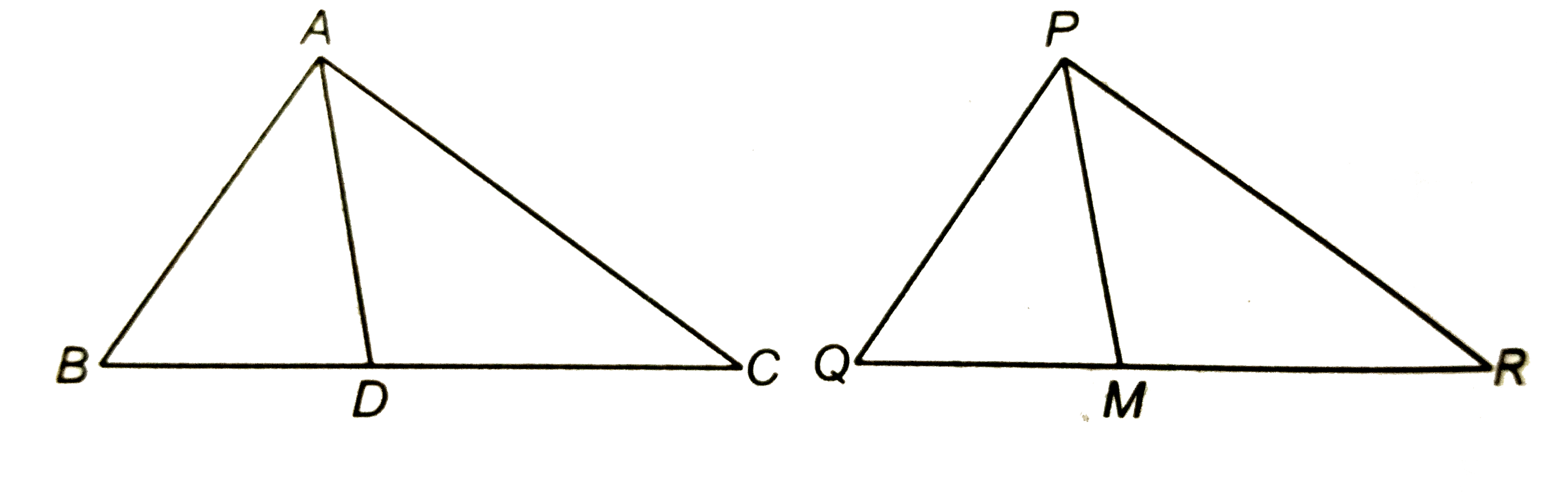
View Solutionएक त्रिभुज ABC की भुजाये AB और BC तथा मध्यिका AD एक अन्य त्रिभुज PQR कि क्रमशः भुजाओ PQ और QR तथा मध्यिका PM के समानुपाती है (देखिये आकृति) दर्शाइए कि `DeltaABC~DeltaPQR` है
View Solutionएक त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि `angleADC=angleBAC` है दर्शाइए कि `CA^2=CB.CD` है
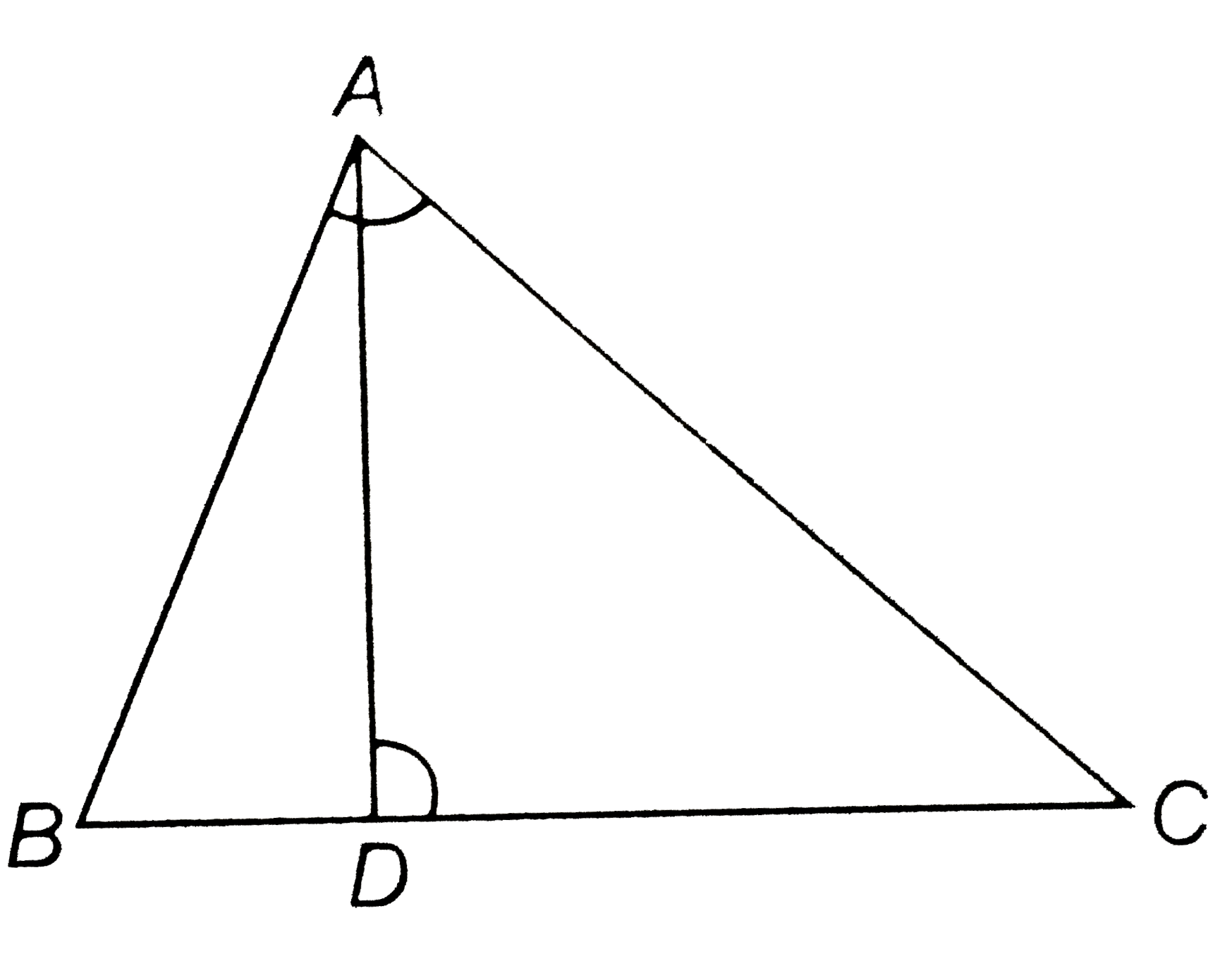
View Solutionएक त्रिभुज ABC की भुजाये AB और AC तथा मध्यिका AD एक अन्य त्रिभुजों PQ और PR तथा मध्यिका PM के क्रमशः समानुपाती है दर्शाइए कि `DeltaABC~DeltaPQR` है
View Solutionलम्बाई 6 मी वाले एक ऊर्ध्वाधर स्तम्भ की भूमि पर छाया की लम्बाई 4 मी है जबकि उसी समय एक मीनार की छाया कि लम्बाई 28 मी है मीनार कि ऊंचाई ज्ञात कीजिये
View SolutionAD और PM त्रिभ्जो ABC और PQR में क्रमशः ,मध्यिकाये है जबकि `DeltaABC~DeltaPQR` है सिद्ध कीजिये कि `(AB)/(PQ)=(AD)/(PM)` है
View Solution
एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.3) questions and complete solutions for chapter त्रिभुज of NAGEEN MATHS (HINDI) of Class 10
All Exercises from MADHUR GUPTA Class 10 MATHS त्रिभुज
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.1)
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.2)
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.3)
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.4)
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.5)
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.6 (ऐच्छिक))
- प्रश्नावली 6A
- प्रश्नावली 6B
- प्रश्नावली 6C
- प्रश्नावली 6D
- विविध प्रश्नावली (अति लघु उत्तरीय प्रश्न)
- विविध प्रश्नावली (दीर्घ उत्तरीय प्रश्न)
- विविध प्रश्नावली (बहु विकल्पीय प्रश्न)
- विविध प्रश्नावली (लघु उत्तरीय प्रश्न)
- साधित उदाहरण