Complete Solutions to प्रश्नावली 6D of chapter त्रिभुज of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | त्रिभुज |
| MADHUR GUPTA | प्रश्नावली 6D |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
निम्नलिखित प्रत्येक में बताइये कि त्रिभुज कि भुजाये समकोण बनती है या नहीं
(i) 9 सेमी , 12 सेमी और 15 सेमी
(ii) 8 सेमी , 15 सेमी और 17 सेमी
(iii) 7 सेमी , 24 सेमी और 25 सेमी
View Solutionसमकोण `DeltaABC` में , `angleC` समकोण है
(i) AB=1.7 सेमी, BC=1.5 सेमी, तो CA ज्ञात कीजिए
CA=2.4 सेमी, AB=4.0 सेमी तो BC ज्ञात कीजिए
View Solutionएक सीढ़ी सड़क के एक ओर जमीन से 15 मीटर ऊँची खिड़की तक पहुँचती है इसके पाद को उसी स्थान पर रखकर , सीढ़ी को दूसरी ओर घुमाने पर यह 8 मीटर ऊँची खिड़की पर पहुँचती है यदि सीढ़ी की लम्बाई 17 मीटर है तो सड़क की चौड़ाई ज्ञात कीजिये
View Solutionएक व्यक्ति 40 मी उत्तर में तथा इसके बाद 50 मी पश्चिम में जाता है इसकी प्रारम्भिक बिंदु से दूरी ज्ञात कीजिये
View Solutionकिसी समचतुर्भुज की भुजाओं में प्रत्येक 13 सेमी है एवं एक विकर्ण 24 सेमी है, तो दूसरे विकर्ण की लंबाई है
View Solutionसंलग्न चित्र में , `anglePSQ=90^@` , PQ=10 सेमी , QS= सेमी और RQ=9 सेमी तो PR की लम्बाई ज्ञात कीजिये
View SolutionABC एक समद्विबाहु समकोण त्रिभुज है जिसमे C समकोण है सिद्ध कीजिये कि `AB^2=2AC^2`
View Solution`DeltaABC` एक समद्विबाहु त्रिभुज है जिसमे AC=BC है यदि `AB^2=2AC^2` तो सिद्ध कीजिये कि `DeltaABC` समकोणीय है

View Solutionसमबाहु `DeltaABC` में A से भुजा BC पर लम्ब AD है सिद्ध कीजिये कि `3AB^2=4AD^2`
View Solution`Delta PQR` में `angleQ` समकोण है भुजाओ QR और PQ पर क्रमशः बिन्दु M और N है सिद्ध कीजिये कि `PM^2+RN^2=PR^2+MN^2`
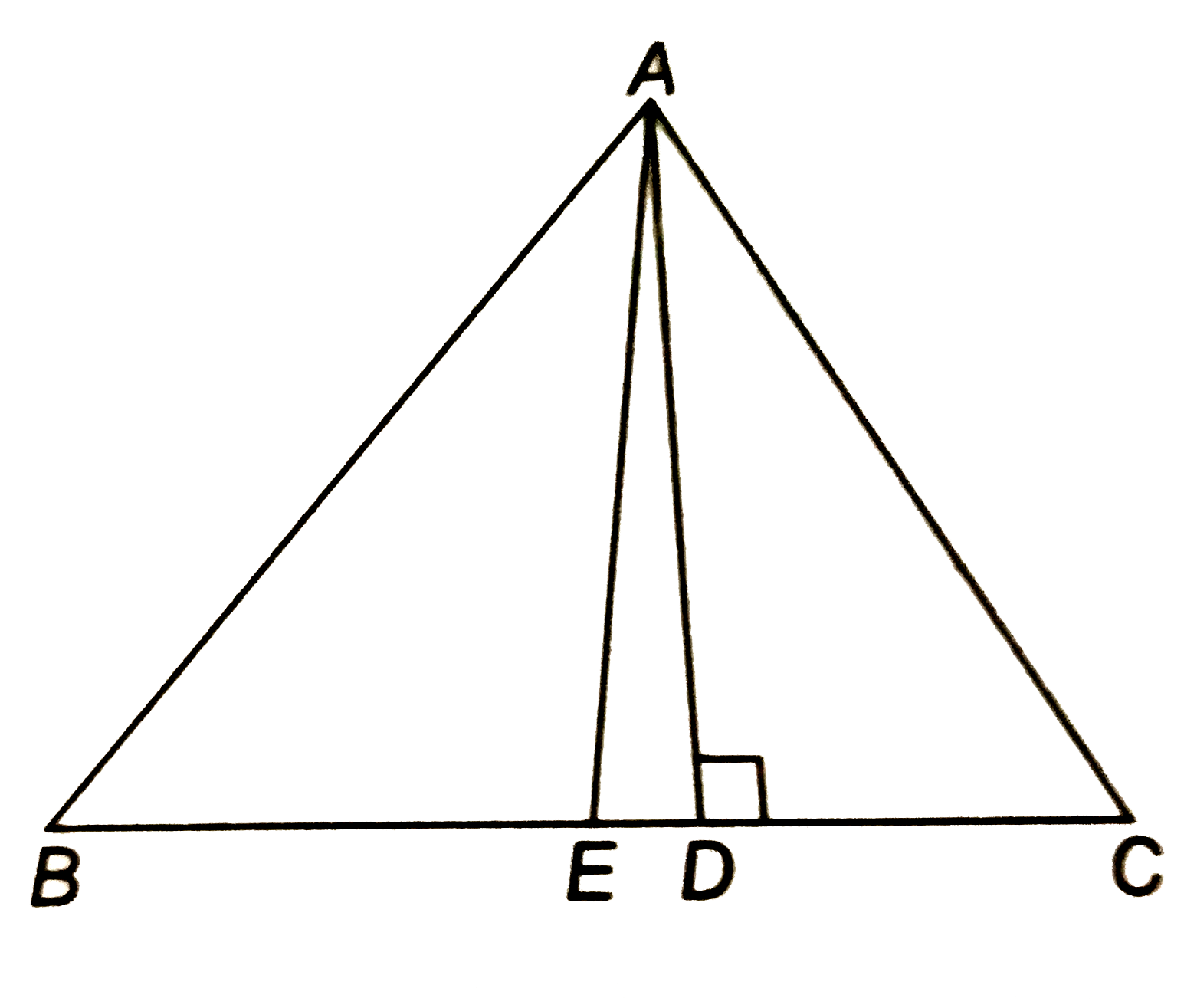
View Solutionदिए चित्र में एक त्रिभुज ABC है जिसमे `ABgtAC` है BC का मध्य बिन्दु E तथा BC पर लम्ब AD है सिद्ध कीजिये कि `AB^2 +AC^2 =2AE^2 +2BE^2`
View Solutionवर्ग ABCD में सिद्ध कीजिये कि `AC^2=2AB^2`
View Solutionसमचतुर्भुज ABCD में सिद्ध कीजिये कि `AC^2+BD^2=4AB^2`
View Solution`DeltaABC` में `angleA=90^@` CA=AB और बढ़ाई गयी AB पर एक बिन्दु D है सिद्ध कीजिये कि
`DC^2-BD^2=2AB.AD`
View Solutionन्यूनकोणीय `DeltaABC` में AD मध्यिका तथा AE शीर्ष लम्ब है सिद्ध कीजिये कि : `AC^2=AD^2+BCxxDE+1/4BC^2` `AB^2=AD^2-BCxxDE+1/4BC^2`
`AC^2+AB^2=2AD^2+1/2BC^2`
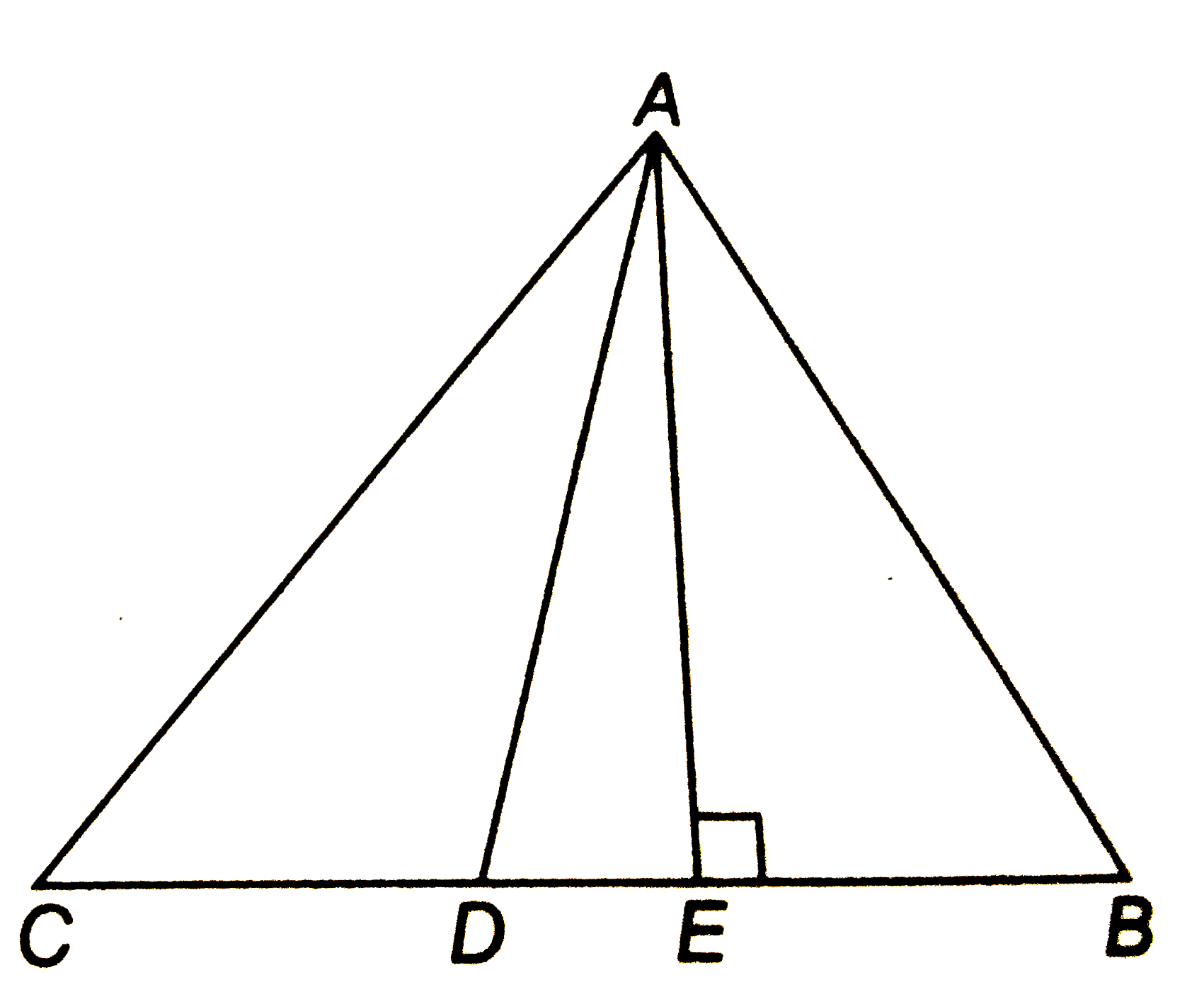
View Solutionसंलग्न चित्र में , ABC एक त्रिभुज है जिसमे AD मध्यिका है और `AEbotBC` है सिद्ध कीजिये कि
`2AB^2+2AC^2=4AD^2+BC^2`
View Solution`DeltaABC` के अन्दर स्थित बिंदु O से भुजाओ BC , CA और AB पर क्रमशः OD , OE और OF लम्ब डाले गए है सिद्ध कीजिये कि
(i) `4F^2+BD^2+CE^2=OA^2+OB^2+OC^2-OD^2-OE^2-OF^2`
(ii) `AF^2+BD^2+CE^2=AE^2+CD^2+BF^2`
View Solutionन्यूनकोण त्रिभुज ABC में , AD इसकी मध्यिका है सिद्ध कीजिये कि :
`AD^2=(AB^2)/2+(AC^2)/2-(BC^2)/4`
View Solutionसमकोण `DeltaABC` में `angleA=90^@` तथा AD भुजा BC पर लम्ब है सिद्ध कीजिये कि
`AB^2-BD^2=AC^2-CD^2`
View Solutionदिए चित्र में `DeltaABC` में `angleB` समकोण है मध्यिकाओ AD और CE की लम्बाईयाँ क्रमशः 5 सेमी और `2sqrt5` सेमी है AC की लम्बाई ज्ञात कीजिये

View Solution`DeltaABC` की भुजा BC को समत्रिभाजित करने वाला बिन्दु L बिन्दु B के पास है सिद्ध कीजिये कि
`2AB^2+AC^2=3AL^2+2BL^2+CL^2`
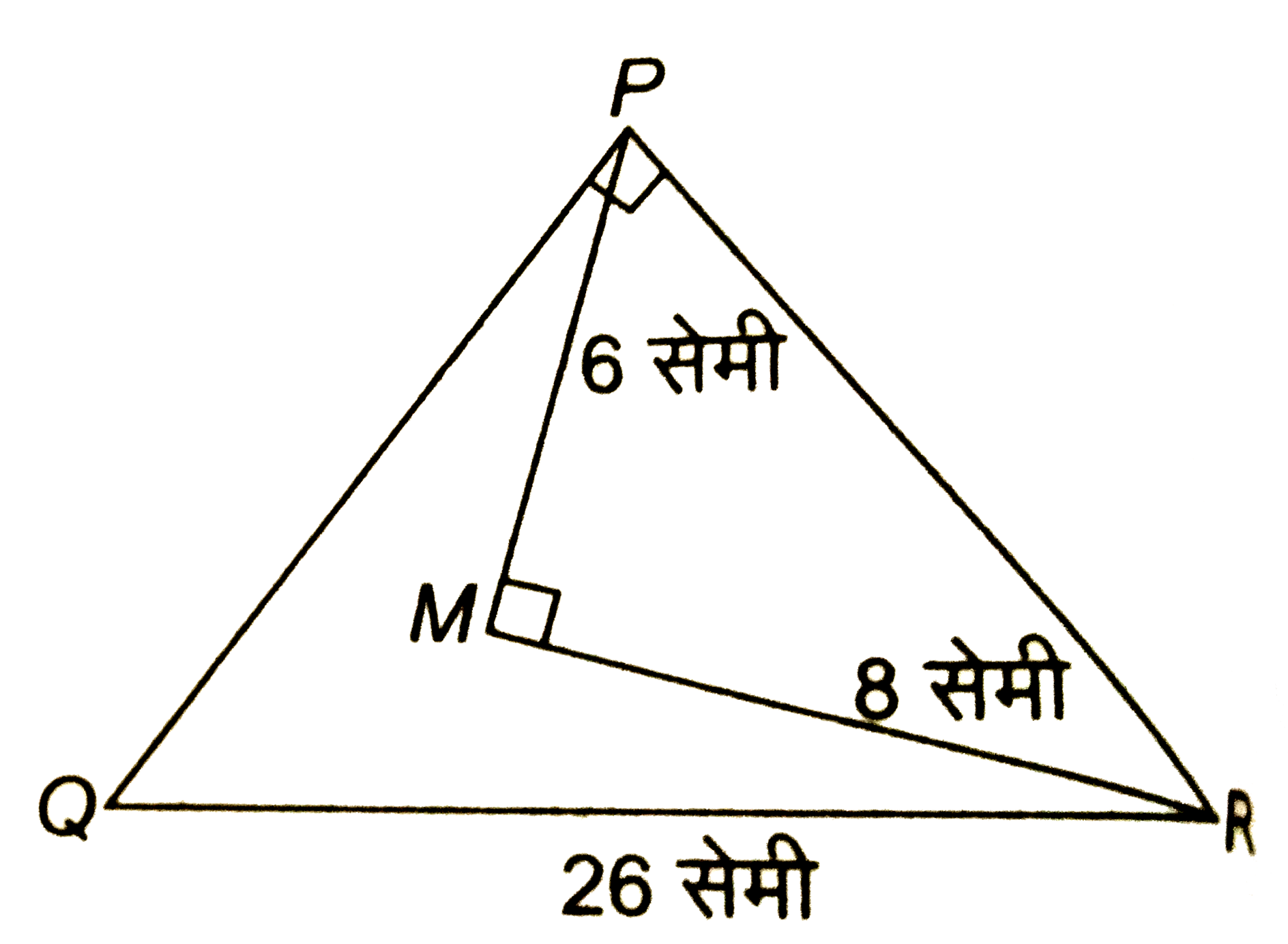
View Solutionदिए चित्र में `angleQPR=90^@` , QR=26 सेमी , PM=6 सेमी , MR=8 सेमी और `anglePMR=90^@` है `DeltaPQR` का क्षेत्रफल ज्ञात कीजिये
View Solutionएक समकोण त्रिभुज ABC दिया है समकोण बनाने वाली भुजाएँ 6 सेमी और 8 सेमी है `DeltaABC` के अंतर्गत एक वृत्त बनाया गया है इस वृत्त की त्रिज्या ज्ञात कीजिये
View Solutionएक न्यूनकोण त्रिभुज में , इसकी एक मध्यिका को इसकी भुजाओ के पदों में व्यक्त कीजिये
View Solutionएक चतुर्भुज ABCD में `angleB=90^@` और `AD^2=AB^2+BC^2+CD^2` है सिद्ध कीजिये कि `angleACD=90^@`
View SolutionABC एक समकोण त्रिभुज है जिसमे समकोण है और `AC=sqrt3BC` है सिद्ध कीजिये कि `angleABC=60^@`
View Solution`DeltaABC` में `angleA =60^@` है सिद्ध कीजिये कि `BC^2=AB^2+AC^2-AB.AC.`
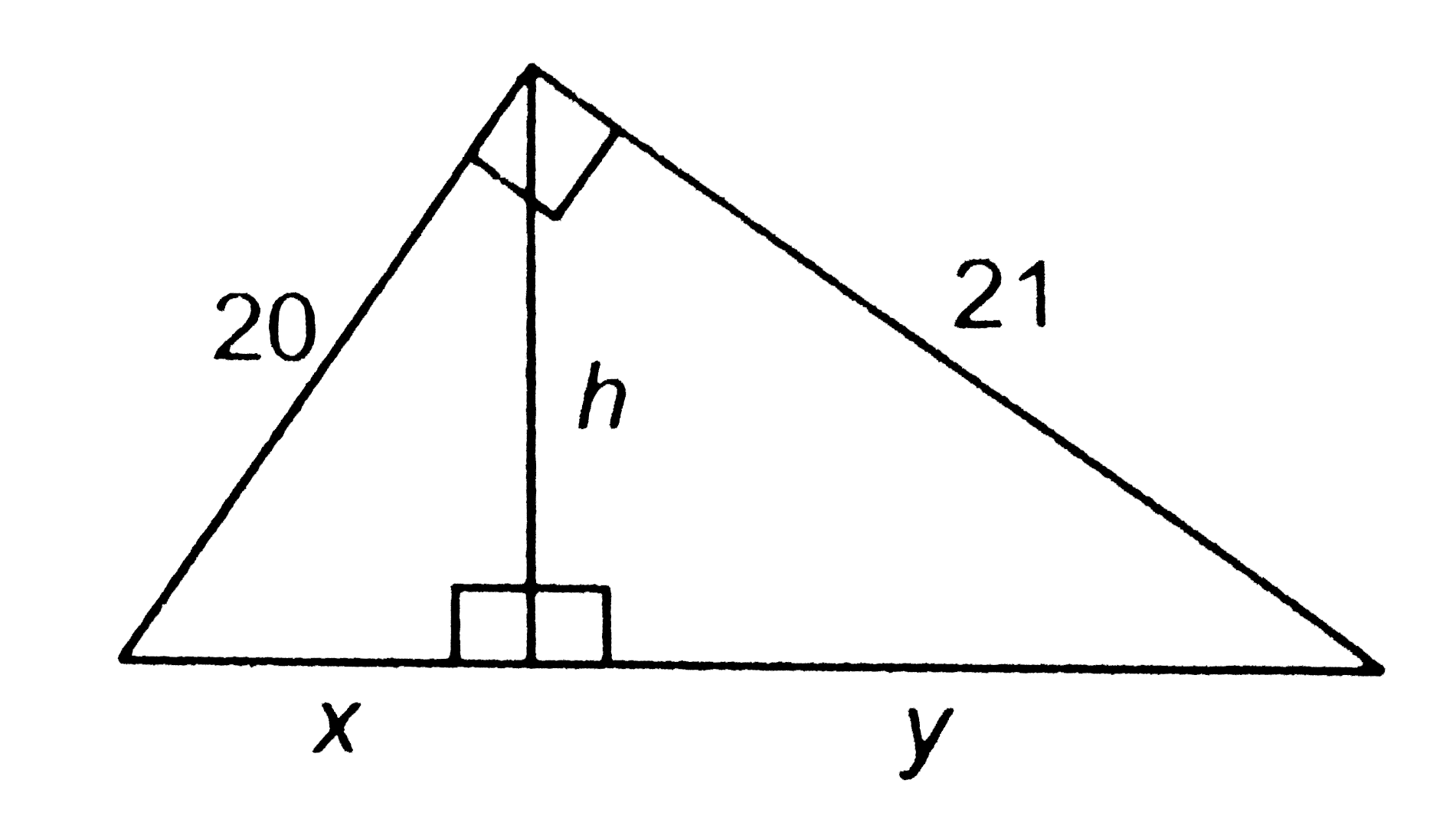
View Solutionसंलग्न चित्र में, x,y और h ज्ञात कीजिये
View Solution
प्रश्नावली 6D questions and complete solutions for chapter त्रिभुज of NAGEEN MATHS (HINDI) of Class 10
All Exercises from MADHUR GUPTA Class 10 MATHS त्रिभुज
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.1)
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.2)
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.3)
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.4)
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.5)
- एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.6 (ऐच्छिक))
- प्रश्नावली 6A
- प्रश्नावली 6B
- प्रश्नावली 6C
- प्रश्नावली 6D
- विविध प्रश्नावली (अति लघु उत्तरीय प्रश्न)
- विविध प्रश्नावली (दीर्घ उत्तरीय प्रश्न)
- विविध प्रश्नावली (बहु विकल्पीय प्रश्न)
- विविध प्रश्नावली (लघु उत्तरीय प्रश्न)
- साधित उदाहरण