CD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक है कि बिंदु D और H क्रमशः ΔABC और ΔFEG की भुजाओ AB और FE पर स्थित है यदि ΔABC~DE<aFEG है तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGF
(iii) ΔDCA~ΔHGF
ΔACD और ΔFGH में
∠CAD=∠GFH …(1) (∴ΔABC~ΔFEG)
परन्तु ΔABC~ΔFEG दिया है
∴ ∠C=∠G ⇒ ∠ACD=∠FGH …(2)
समीकरण (1) और (2) से
ΔACD~ΔFGH (A.A समरूपता से)
⇒CDGH=ACFG
(ii) ΔABC~ΔFEG⇒∠ACB=∠FGB
⇒12∠ACB=12∠FGE
⇒∠DCB=∠HGE
तथा ∠DBC=∠HEG (∴ΔABC~ΔFEG⇒∠B=∠E)
∴ ΔDCB~ΔHGE (A.A समरूपता से)
(iii) ΔABC~ΔFEG
∴ ∠CAB=∠GFE
⇒ ∠CAD=∠GFH
⇒ ∠DAC=∠HFG
तथा ΔABC~ΔFEG
⇒ ∠ACB=∠FGE
⇒ 12∠ACB=12∠FGE
∠DCA=∠HGF
अब ∠DAC=∠HFG
अब ∠DCA=∠HGF
∴ ΔDCA~ΔHGF (A.A समरूपता) यही दर्शाना था
Topper's Solved these Questions
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.4)
9 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.5)
17 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - एन0 सी0 आर0 टी0 प्रश्न (प्रश्नावली 6.2)
10 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग BOOK - NOOTAN HINDICHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - विविध प्रश्नावली (दीर्घ उतरिये प्रश्न)
6 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - NOOTAN HINDICHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - विविध प्रश्नावली (बहुविकल्पीय प्रश्न)
7 Videos
Similar Questions
मान लीजिये ΔABC~ΔDEF है और इनके क्षेत्रफल क्रमशः 64 सेमी2 और 121 सेमी2 है यदि EF=15.4 सेमी हो तो BC ज्ञात कीजिये
View Solutionकुछ त्रिभुजों कि भुजाये नीचे दी गयी है निर्धारित कीजिये कि इनमे से कोण-कोण से त्रिभुज समकोण त्रिभुज है इस स्थिति में कारण कि लम्बाई भी लिखिए
(i) 7cm,24cm,25cm
(ii) 3cm,8cm,6cm
(iii) 50cm,80cm,100cm
(iv) 13cm,12cm,5cm
View Solutionआकृति (i) और (ii) में , DE || BC है (i) में EC और (ii) में AD ज्ञात कीजिये
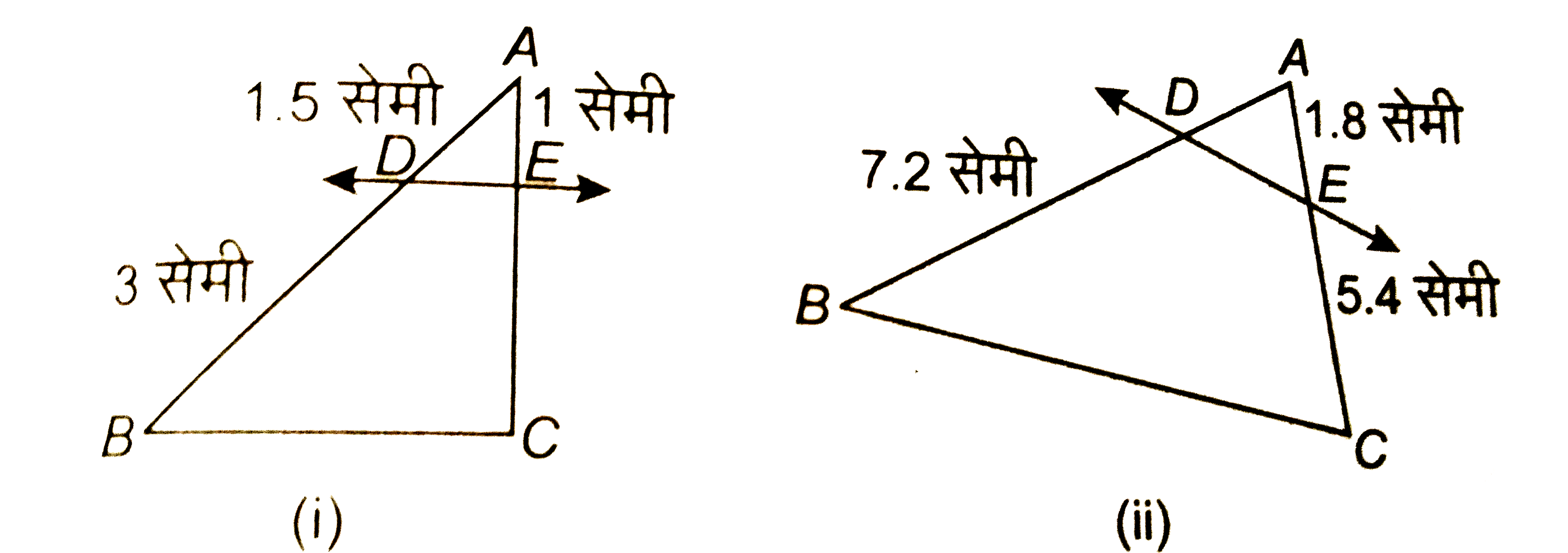
View Solutionकिसी सीधी क्षैतिज सड़क के ऊपर एक हवाई जहाज क्रमागत किलोमीटर के दो पत्थरों के बीच उड़ रहा है। ये पत्थर हवाई जहाज के दोनों ओर स्थित हैं। हवाई जहाज से पत्थरों के अवनतांश 30∘ और 60∘ हैं। सड़क से वायुयान की ऊँचाई मीटर में ज्ञात कीजिए।
View Solutionसमीकरण 5x−15y=16 और 3x−9y=485 के युग्म का के हल होंगे :
View SolutionCD और GH क्रमशः ∠ACB और ∠EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः ΔABC और ΔEFG की भुजाओं AB और FE पर स्थित हैं । यदि ΔABC~ΔFEG तो दर्शाइए कि
(i) CDGH=ACFG
(ii) ΔDCB~ΔHGE
(iii) ΔDCA~ΔHGF
View SolutionCD and GH are the bisectors of ∠ACB and ∠EGF respectively. If D lies on AB of ΔABC and H lies on EF of ΔEFG and if ΔABC~ΔEFG, then prove that (a) CDGH=ACFG, (b)ΔDCB~ΔHGE, (c)ΔDCA~ΔHGF
View Solutionदो स्थिर बिंदु A और B के निर्देशांक क्रमशः (a,0) और (−a,0) है , तो चर बिंदु P का बिन्दुपथ ज्ञात कीजिए जबकि :
PA=nPB , जहाँ n अचर है ।
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
CDGH=ACFG
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABCandΔFEG respectively. IF ΔABC~ΔFEG then show that
ΔDCA~ΔHGF
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
CDGH=ACFG
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCB~ΔHGE
View SolutionGD and GH are respectively the bisectors of ∠ACBand∠EGF such that D and H lie on sides AB and FE of ΔABCandandΔEFG respectively. If ΔABC~ΔFEG , show that:
ΔDCA~De<HGF
View SolutionCD and GH are respectively the bisectors of ⌊ACBand⌊EGF such that D and H lie on sidea AB and FE of ΔABCandΔEFG respectively. If ΔABC~ΔFEG, show that.
i] CDGH=ACFG
ii] ΔCDB~ΔHGE
iii] ΔDCA~ΔHGF
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
CDGH=ACFG
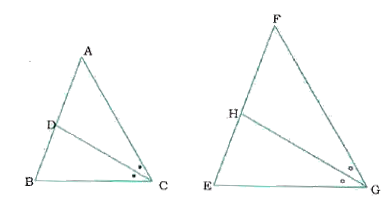
View SolutionCD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC~ΔFEG, show that :
ΔDCB~ΔGHE
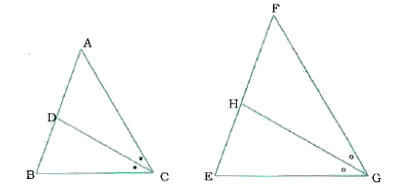
View Solution
