Complete Solutions to EXAMPLE of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| R G PUBLICATION | EXAMPLE |
| Number Of Questions | 68 |
| Academic Year | 2023-24 |
In `triangleABC` two points L and M are taken in the sides AB and AC such that `LM|\|BC` and BL=x-3,AB=2x,CM=x-2,AC=2x+3 then find the value of x.
View SolutionIn the given figure `DE|\|BC`,If `(AD)/(DB)=2/3 `and AC=18 cm.then find AE.

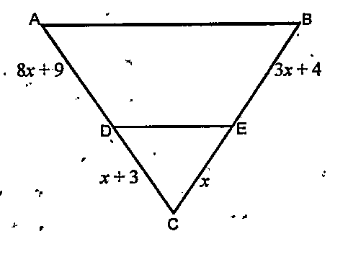
View SolutionIn the given figure for what value of x will be `DE|\|AB?
View SolutionIn `triangle ABC`D and E are respectively two points on the side AB and AC.AB=12 cm,AD=8 cm,AE=12 cm and AC=18 cm then show that `DE|\|BC`.
View SolutionD and E are respectively the point on the sides AB and AC of a trinagle ABC such that `DE|\|BC`. Through the point E a line parallel to CD is drawn which cut AB at the point F then show that `AD^2=ABxxAF`
View SolutionABC is an isosceles triangle with AB = AC and D is a point on AC such that `BC^2=ACxxCD`. Prove that BD = BC
View SolutionIf `triangle ABC`is similar to `triangleDEF` such that BC = 4 cm, EF = 5 cm and area of `triangleABC = 64cm^2`. Determine the area of `triangleDEF `
View SolutionIn `triangleABC`if `AD_|_BC` and `AD^2=BDxxDC` then prove that, `angleBAC =90^@`
View SolutionD and E are two points on the sides AC and AB respectively of `triangleABC`such that `triangle ADE~triangleABC`.If AD=1.9cm,AE=3.6cm.BE=2.1cm.and BC=8.4 cm.find DE.
View SolutionD is a point on the side BC of a triangle ABC such that`angleADC=angleBAC`.Show that`CA^2=CB.CD`.
View SolutionIf BD and CE are two altitudes of `triangleABC`,prove that`(CA)/(AB)=(CE)/(DB)`
View Solution`triangleBAC and triangleBDC` are two right-triangle on the same side of the base BC.If AC ans DB intersect each other at a point P,show that `APxxPC=DPxxPB`.
View SolutionIf BD is the perpendicular drawn from the vertex B of the right triangle ABC to the hypotenuse AC,prove that(i)`BD^2=ADxxDC`
View SolutionIf BD is the perpendicular drawn from the vertex B of the right triangle ABC to the hypotenuse AC,prove that(ii)`AB^2=ADxxAC`
View SolutionIf BD is the perpendicular drawn from the vertex B of the right triangle ABC to the hypotenuse AC,prove that(iii)`BC^2=CDxxAC`
View SolutionABC is an isosceles triangle with AB = AC and D is a point on AC such that `BC^2=ACxxCD`. Prove that BD = BC
View SolutionIf AD is the altitudè of `triangleABC and (BD)/(DA)=(DA)/(DC) `prove that `triangleABC` is right-angled
View SolutionD and E are respectively two points on the sides AB and AC of `triangleABC` such that `DE||BC`.If (AD)/(DB)=2/3 find (BC)/(DE)
View SolutionOf the trapezium ABCD, `AB||DC` and DC = 2AB. If the line segment EF drawn parallel to AB meets AD and BC at the points Fand E respectively so that (BE)/(EC)=3/4 and the diagonal DB meets EF at the points G, prove that 7FE=11AB
View SolutionAB and EF are two parallel line segments and D is the point of intersection of BE and AF. C is a point on AE such that `CD||AB`. If AB = 6 cm., EF = 10cm .,BD = 4 cm.,find the lengths of CD and DE.
View SolutionProve that in two equiangular triangles the ratio of the corresponding sides and the ratio of the bisectors of the corresponding angles are equal. [The end-points of the bisectors are on the opposite sides of the angles.]
View SolutionProve that in two similar triangles the ratio of corresponding sides is equal to the ratio of the corresponding altitudes.
View SolutionIf two sides and the median drawn to one of these two sides of a trlangle are proportional to the corresponding sides and median of another triangle,prove that the two triangles are similar.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding altitudes of the triangles.
View SolutionProve that the ratio of the areas of two similar triangle is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the ratio of the areas of two similar triangles is equal to the ratio of the squares of the bisectors of the corresponding angles of the triangles. [The end-points of the angular bisectors are on the opposite sides of the angles.]
View SolutionProve that the area of an equilateral triangle with sides equal to the sides of a square is half the area of the equilateral triangle with sides equal to țhe length of the diagonals of the square.
View SolutionFind the length of the hypotenuse of the triangles whose other two sides are:(i)6cm ,8 cm
View SolutionFind the length of the hypotenuse of the triangles whose other two sides are:(ii)24 cm ,7 cm
View SolutionFind the length of the hypotenuse of the triangles whose other two sides are:(iii)5 cm ,12 cm
View SolutionIn the `triangle ABC,AB=p^2-q^2,BC=p^2+q^2` and CA=2pq then prove that `triangleABC`is right angled.Which of the angles of the triangle is right angle?
View SolutionProve that the sum of the squares of the sides of a rhombus is equal to the sum of the squarea of its diagonals.
View SolutionProve that the sum of the squares drawn on the sides of a square is equal to the sum of the squares drawn on its diagonals.
View SolutionIf one side of an equilateral triangle measures 5 cm,then find the measure of its altitude.
View SolutionThe sides of a triangle measure 13 cm,12 cm,and 5 cm.prove that the triangle is right angled.
View SolutionOf the right triangle ABC,`AB=a+b,BC=2sqrt(ab) and anglec=90^@` .Find AC.
View SolutionOf the right triangle PQR PQ = ax - by, QR = bx + ay and `angleQ`=Right angle then find PR
View SolutionA man walked 7 km. to the north and then turning to the east , walked 3 km.Finally he turned to the south and walked 3 km.Find the minimum distance between the starting point and the finishing point of his journey.
View Solution`angleQ of trianglePQR` is a right angle.If PQ=4 cm,QR=3cm,then find the length of the median drawn from Q to PR.
View SolutionThe length of the hypotense of an isosecles right, triangle is `4sqrt2`.Find the length of its side.
View SolutionIf the length of the diagonals of a rhombusare 10 cm and 24 cm. then find the length of its sides.
View SolutionIf the length of one side of an equilateral triangle is 10 cm. then find the length of its altitude.
View SolutionIf the length of the diagonals of a rhombus are 18 cm and 24cm. then find the length of sides.
View SolutionIf the length of one of the diagonals of a rhombus is 24 cm. and the length of one of its sides is 15 cm.find the length of the other diagonal.
View SolutionIf `angleC` of the isosceles triangle ABC is measure `90^@`, then prove that`AB^2=2AC^2`.
View SolutionIf PS is the altitude on the base QR `trianglePQR`,then prove that `PQ^2+SR^2=PR^2+QS^2`
View SolutionIf ABCD is a square, then show that `AC^2=2AB^2`
View SolutionThe sides of the quadriIateraI ABCD are not equal to one another and `AC_|_BD` prove that `AB^2+CD^2=AD^2+BC^2`
View SolutionP is any point inside the rectangle ABCD. Prove that `AP^2+CP^2=BP^2+DP^2`
View SolutionProve that the area of the equilateral triangle drawn on the hypotenuse of a right angle triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides.
View SolutionAD is the perpendicular from A and BC of `triangleABC`.If AB=c,BC=a,CA=b and AD=x then prove that `a=sqrt(b^2-x^2)+sqrt(c^2-x^2)`
View SolutionOf triangle ABC,`angleB=90^@ and BD_|_AC`.IF AB=c,BC=a,CA=b and BD=p then prove that ,`1/p^2=1/a^2+1/c^2`.
View SolutionThe square of the length of the hypotenuse of an isosceles right triangle is `32cm^2`.Find the length of the other two sides.
View SolutionIf one diagonal of a square measures `12sqrt2`cm. find the length of its side.
View SolutionIf one side of an equilateral triangle measures 10cm. find its height.
View SolutionThe perimeter of two similar triangles are respectively 25cm. and 15 cm. If one side of the first triangle is 9 cm.,find the corresponding side of the second triangle.
View SolutionIn triangle ABC,D and E are points on the sides AB and AC such that `angleAED=angleC`. Prove that `triangleADE~triangleABC`
View Solution`triangleBAC and triangleBDC` are two right-triangle on the same side of the base BC.If AC ans DB intersect each other at a point P,show that `APxxPC=DPxxPB`.
View SolutionM is the mid point of the side CD of the parallelogram ABCD. The line BM is drawn intersecting AC in L and AD produced Prove that (i)`ALxxLM=CLxxBL`
View SolutionM is the mid point of the side CD of the parallelogram ABCD. The line BM is drawn intersecting AC in L and AD produced at E.Prove that(ii) EL = 2BL
View SolutionIn trapezium ABCD ,`AB||DC` and AC and BD diagonal intersect at the point E. Prove that (EA)/(EC)=(EB)/(ED).
View SolutionThe bisector of `angleC and angleG`of two similar triangle ABC and EFG are meet the side AB and EF respectively at the point D and H.Prove that`triangleDCA~triangleHGE`
View SolutionIn the right triangleACB,`angleC=90^@ and CD_|_AB`.Prove that,`(BC^2)/(AC^2)=(BD)/(AD)`
View Solution`PA_|_AC and RC_|_AC`such that PA=x and RC = z .If PC and AR are intersect at thepoint Q , perpendicuIar distance from AC is y then prove that 1/x+1/z=1/y.
View SolutionIf two triangles are equiangular then prove that the ratio of the corresponding sides is (i)Same as the ratio of the corresponding sides.
View SolutionProve that in two equiangular triangles the ratio of the corresponding sides and the ratio of the bisectors of the corresponding angles are equal. [The end-points of the bisectors are on the opposite sides of the angles.]
View SolutionIf two triangles are equiangular then prove that the ratio of the corresponding sides is (iii)Same as the ratio of the corresponding altitude.
View SolutionIf one angle of a triangle is equal to one angle of another triangle and the bisectors of these equal angles divide the opposite side in the same ratio then show that the triangle are similar.
View Solution
EXAMPLE questions and complete solutions for chapter TRIANGLES of R G PUBLICATION of Class 10