Complete Solutions to EXERCISE of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| R G PUBLICATION | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
All circles are ______ . (congruent, similar)
View SolutionAll squares are __-. (Similar, congruent)
View SolutionAll____ triangles are similar. (isosceles, equilateral)
View SolutionTwo polygons of the same number of sides are similar, if(a) their corresponding angles are ___
View SolutionTwo polygons of the same number of sides are similar, if(b) their corresponding sides are___(equal ,proportional)
View SolutionGive two different examples of pair of(i) similar figures
View SolutionGive two different examples of pair of((ii) non-simiIar figures
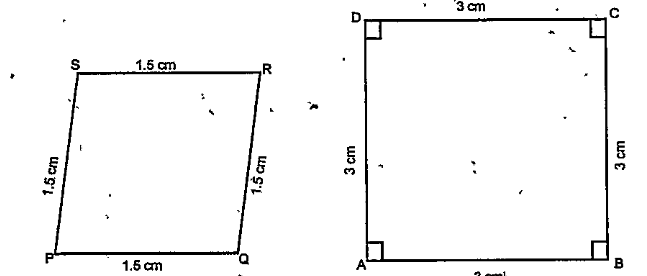
View SolutionState whether foIIowing quadrilaterals are similar or not:
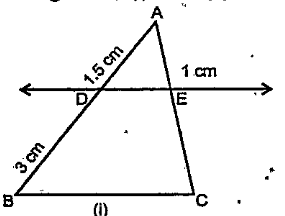
View SolutionIn fig(i) ,`DE||BC`.Find EC in (i).

View SolutionE and F are points on the sides PQ and PR respectively of a `trianglePQR`.For each of the following cases, state whether `EF||QR`:(i)PE = 3.9 cm,EQ = 3 cm,PF= 3.6 cm and FR = 2.4 cm
View SolutionE and F are points on the sides PQ and PR respectively of a `trianglePQR`.For each of the following cases, state whether `EF||QR`:(ii) PE = 4 cm, QE =4.5 cm, PF = 8 cm and RF = 9 cm
View SolutionE and F are points on the sides PQ and PR respectively of a `trianglePQR`.For each of the following cases, state whether `EF||QR`:(iii)PQ =.1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
View SolutionIn Fig. , if `LM||CB` and `LN||CD`,prove that `(AM)/(AB)=(AN)/(AD)`
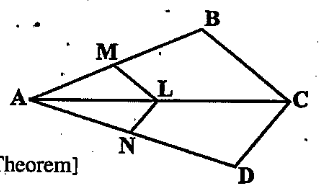
View SolutionIn Fig. `DE||AC and DF||AE`.Prove that `(BF)/(FE)=(BE)/(EC)`

View SolutionIn Fig. 6.20, `DE||OQ and DF||OR`.Show that `EF||QR`.

View SolutionIn Fig., A, B and C are points on OP, OQ and OR respectively such that `AB||PQ and AC||PR`.Show that `BC||QR`.
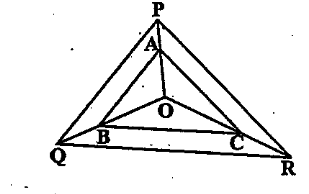
View SolutionUsing Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.. (Recall that you have proved it in class IX).
View SolutionUsing Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in class IX).
View SolutionABCD is a trapezium in which `AB||DC`and its diagonals intersect each other at the point O.Show that `(AO)/(BO)=(CO)/(DO)`
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that (AO)/(BO)=(CO)/(DO)`. Show that ABCD is a trapezium.
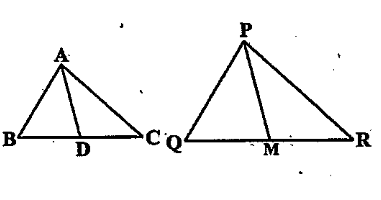
View SolutionState which pairs of triangles in Fig. are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
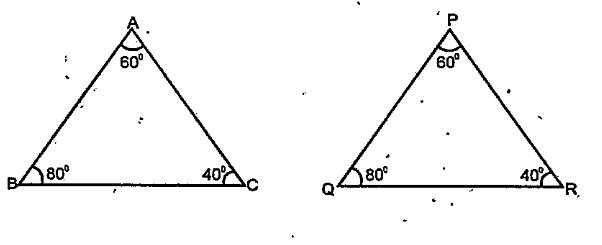
View SolutionState which pairs of triangles in Fig. are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
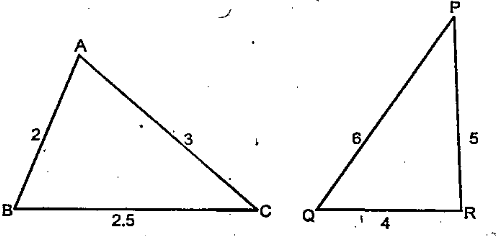
View SolutionState which pairs of triangles in Fig.are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
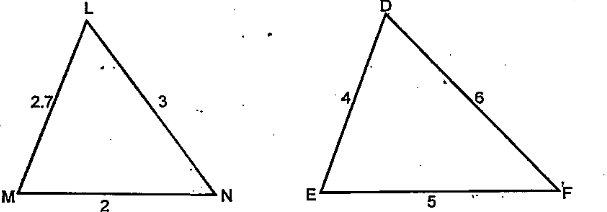
View SolutionState which pairs of triangles in Fig.are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
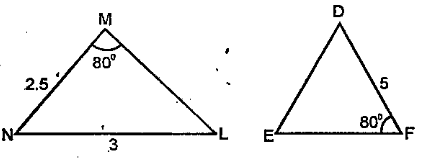
View SolutionState which pairs of triangles in Fig.are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

View SolutionState which pairs of triangles in are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

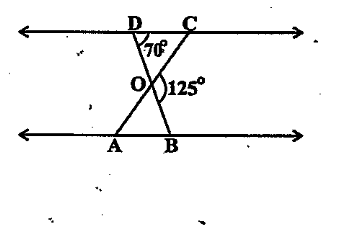
View SolutionIn Fig. 6.35, `triangleODC~triangleOBA,angleBOC=125^@ and angle CDO=70^@` Find `angle DOC,angle DCO,and angle OAB`.
View SolutionDiagonals AC and BD of a trapezium ABCD with `AB||DC` intérsect each other at the point O.Using a similarity ciiterion for two triangles, show that `(OA)/(OC)=(OB)/(OD)`.
View SolutionIn Fig. 6.36, `(QR)/(QS)=(QT)/(PR)` and `angle 1=angle 2`.Show that `trianglePQS~triangle TQR`

View SolutionS and T are points on sides PR and QR of `triangle PQR` such that `angleP=angleRTS`.Show that`triangleRPQ~triangleRTS`
View SolutionIn Fig.6.38,altitudes AD and CE of `triangleABC`intersect each other at the point P.Show that:
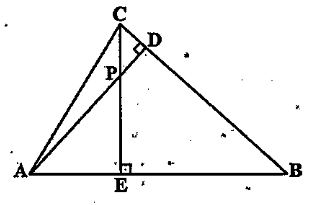 (i)`triangleAEP~triangleCDP`
(i)`triangleAEP~triangleCDP`
View SolutionIn Fig.6.38,altitudes AD and CE of `triangleABC`intersect each other at the point P.Show that:
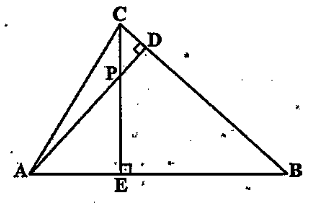 (ii)`triangleABD~triangleCBE`
(ii)`triangleABD~triangleCBE`
View SolutionIn Fig.6.38,altitudes AD and CE of `triangleABC`intersect each other at the point P.Show that:
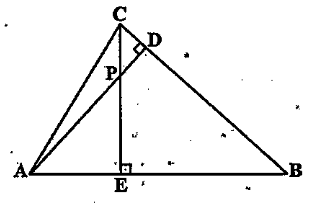 (iii)`triangleAEP~triangleADB`
(iii)`triangleAEP~triangleADB`
View SolutionIn Fig.6.38,altitudes AD and CE of `triangleABC`intersect each other at the point P.Show that:
 (iv)`trianglePDC~triangleBEC`
(iv)`trianglePDC~triangleBEC`
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that `triangleABE~triangleCFB`.
View SolutionIf Fig. 6.3 ,ABC and AMP are two right triangles right angled at B and M respectively.Prove that :(i)`triangleABC~triangleAMP`
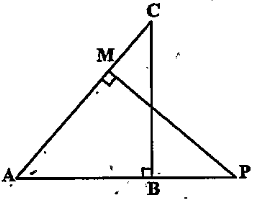
View SolutionIf Fig. 6.3 ,ABC and AMP are two right triangles right angled at B and M respectively.Prove that :
 (ii)`(CA)/(PA)=(BC)/(MP)`
(ii)`(CA)/(PA)=(BC)/(MP)`
View SolutionCD and GH are respectively the bisectors of `angleACB and angleEGF`such that D and H lie on sides AB and FE of `triangleABC and triangleFEG` respectively. If `triangleABC~triangleFEG`.show that:(i)`(CD)/(GH)=(AC)/(FG)`
View SolutionCD and GH are respectively the bisectors of `angleACB and angleEGF`such that D and H lie on sides AB and FE of `triangleABC and triangleFEG` respectively. If `triangleABC~triangleFEG`.show that:(ii)`triangleDCB~triangleHGE`
View SolutionCD and GH are respectively the bisectors of `angleACB and angleEGF`such that D and H lie on sides AB and FE of `triangleABC and triangleFEG` respectively. If `triangleABC~triangleFEG`.show that:(iii)`triangleDCA~triangleHGF`
View SolutionIn FIg. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB=AC. If `AD_|_BC` and `EF_|_AC`, prove that `triangleABD~triangleECF`.

View SolutionSides AB and BC and median AD of a triangle ABC are respeetively proportional to sides PQ and QR and median PM of `trianglePQR`(see Fig. 6.41). Show that `triangleABC~trianglePQR`.
View SolutionD is a point on the side BC of a triangle ABC such that`angleADC=angleBAC`.Show that`CA^2=CB.CD`.
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR.Show that `triangleABC~trianglePQR`.
View SolutionA vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long.Find the height of the tower.
View SolutionIf AD and PM are medians of triangles ABC and PQR,respectively where `triangleABC~trianglePQR`,prove that`(AB)/(PQ)=(AD)/(PM)`.
View SolutionLet `triangleABC~triangleDEF` and their areas be,respectively,`64cm^2 and 121cm^2`.If EF=15.4 cm,find bc.

View SolutionDiagonals of a trapezium ABCD with`AB||DC` intersect each other at the point O.If AB=2 CD,find the ratio of the areas of triangle AOB and COD.
View SolutionIf Fig.6.44 ABC and DBC are two triangles on the same base BC.If AD intersects BC atb O,show that `(ar(ABC))/(ar(DBC))=(AO)/(DO)`

View SolutionIf the areas of a similar triangle are equal,prove that they are congruent.
View SolutionD,E and F are respectively the mid-points of sides AB,BC and CA of `triangleABC`.Find the ratio of the areas of `triangleDEF and triangleABC`.
View SolutionProve that the ratio of the areas of two similar triangle is equal to the square of the ratio of their corresponding medians.
View SolutionProve that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC.Ratio of the areas of triangle ABC and BDE is
a)`2:1` b)`1:2` c)`4:1` d)`1:4`
View SolutionSides of two similar triangle are in the ratio 4:9.Areas of these triangle are in the ratio
a)`2:3` b)`4:9` c)`81:16` d)`16:81`
View SolutionSides of triangle are given below.Determine which of them are right triangles.In case of a right triangle,write the length of its hypotenuse.(i)7 cm,24 cm,25cm
View SolutionSides of triangle are given below.Determine which of them are right triangles.In case of a right triangle,write the length of its hypotenuse.((ii)3 cm,5 cm,6 cm
View SolutionSides of triangle are given below.Determine which of them are right triangles.In case of a right triangle,write the length of its hypotenuse.((iii)50cm,80 cm,100 cm
View SolutionSides of triangle are given below.Determine which of them are right triangles.In case of a right triangle,write the length of its hypotenuse.((iv)13 cm,12 cm,5 cm
View SolutionPQR is a triangle right angled at P and M is a point on QR such that `PM_|_QR`.Show that `PM^2=QM.MR`.
View SolutionIn Fig.6.53,ABD is a triangle right angle at A and `AC_|_BD`.Show that
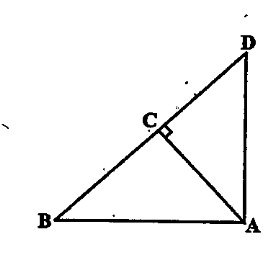 (i)`AB^2=BC.BD`.
(i)`AB^2=BC.BD`.
View SolutionIn Fig.6.53,ABD is a triangle right angle at A and `AC_|_BD`.Show that
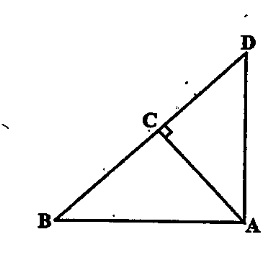 (ii)`AC^2=BC.DC`.
(ii)`AC^2=BC.DC`.
View SolutionIn Fig.6.53,ABD is a triangle right angle at A and `AC_|_BD`.Show that
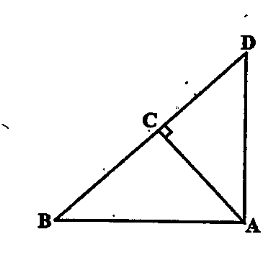 (iii)`AD^2=BD.CD`.
(iii)`AD^2=BD.CD`.
View SolutionABC is an isosceles triangle right angled at C.Prove that`AB^2=2AC^2`.
View SolutionABC is an isosceles triangle with AC=BC.If `AB^2=2AC^2`.prove that ABC is a right triangle.
View SolutionABC is an equilateral triangle of sides 2a.Find each of its altitudes.
View SolutionProve that the sum of the squares of the sides of a rhombus is equal to the sum of the squarea of its diagonals.
View SolutionIn Fig.6.45,O is a point in the interior of a triangle ABC,`OD_|_BC,OE_|_AC and OF_|_AB`.Show that
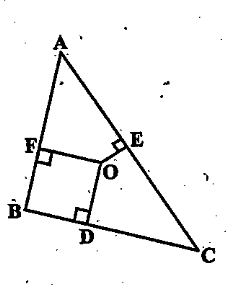 (i)`OA^2+OB^2+OC^2-OD^2-OE^2-OF^2=AF^2+BD^2+CE^2`
(i)`OA^2+OB^2+OC^2-OD^2-OE^2-OF^2=AF^2+BD^2+CE^2`
View SolutionFig.6.45,O is a point in the interior of a triangle ABC,`OD_|_BC,OE_|_AC and OF_|_AB`.Show that
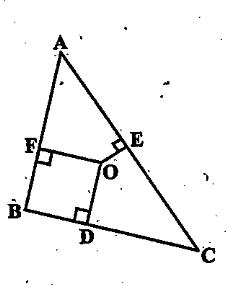 (ii)`AF^2+BD^2+CE^2=AE^2+CD^2+BF^2`
(ii)`AF^2+BD^2+CE^2=AE^2+CD^2+BF^2`
View SolutionA ladder 10 m long reaches a window 8m above the ground. Find the distance of the foot of the ladder from base of the wall.
View SolutionA guy wire attached to a vertical pole of heigh 18 m is 24 m long and has a stake attached to the other end. How far from the base of tho pole should the stake be driven so that the wire will be taut?
View SolutionAn aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the twö planes after `1(1/2)` hours?.
View SolutionTwo poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
View SolutionD and E are points on the sides CA and CB respectively of a triangle ABC right angled at C.Prove that,`AE^2+BD^2=AB^2+DE^2`.
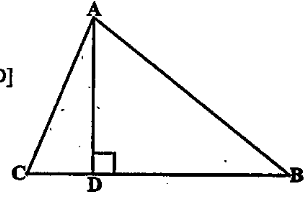
View SolutionThe perpendicular from A on side BC of a`triangleABC` intersects BC at D such that DB = 3 CD (see Fig. 6.55). Prove that `2AB^2=2AC^2+BC^2`.
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD =1/3BC.Prove that `9AD^2=7AB^2`
View SolutionIn an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
View SolutionTick the correct answer and a justify :In `triangleABC,AB=6sqrt3,AC=12cm` and BC=6cm.The angle B is
a)`120^@` b)`60^@` c)`90^@` d)`45^@`
View SolutionIn Fig.6.56,PS is the bisector of `angleQPR of trianglePQR`.Prove that `(QS)/(SR)=(PQ)/(PR)`.

View SolutionIn Fig.6.57,
 D is point on hypothenuse AC of `triangleABC`,such that`BD_|_AC,DM_|_BC and DN_|_AB`.Prove that :(i)`DM^2=DN.MC`
D is point on hypothenuse AC of `triangleABC`,such that`BD_|_AC,DM_|_BC and DN_|_AB`.Prove that :(i)`DM^2=DN.MC`
View SolutionIn Fig.6.58,
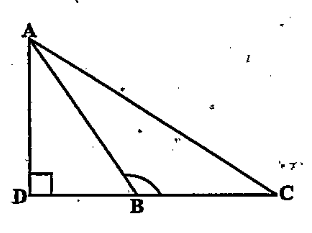 ABC is a triangle in which `angleABC>90^@ and AD_|_CB`produced.Prove that `AC^2=AB^2+BC^2+2BC.BD`.
ABC is a triangle in which `angleABC>90^@ and AD_|_CB`produced.Prove that `AC^2=AB^2+BC^2+2BC.BD`.
View SolutionIn Fig.6.59,
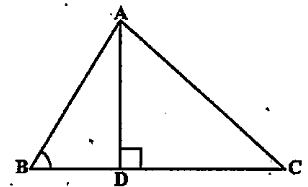 ABC is a triangle in which `angleABC<90^@ and AD_|_BC`.Prove that `AC^2=AB^2+BC^2-2BC.BD`.
ABC is a triangle in which `angleABC<90^@ and AD_|_BC`.Prove that `AC^2=AB^2+BC^2-2BC.BD`.
View SolutionIn Fig.6.60,
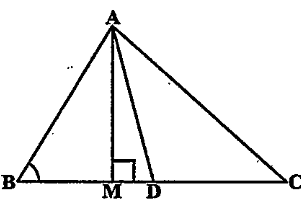 AD is a median of a triangle ABC and `AM_|_BC`.Prove that :(i)`AC^2=AD^2+BC.DM+((BC)/2)^2`
AD is a median of a triangle ABC and `AM_|_BC`.Prove that :(i)`AC^2=AD^2+BC.DM+((BC)/2)^2`
View SolutionIn Fig.6.60,
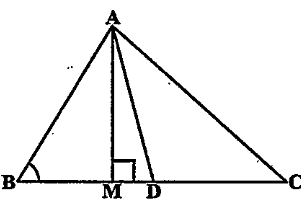 AD is a median of a triangle ABC and `AM_|_BC`.Prove that :(ii)`AB^2=AD^2-BC.DM+((BC)/2)^2`
AD is a median of a triangle ABC and `AM_|_BC`.Prove that :(ii)`AB^2=AD^2-BC.DM+((BC)/2)^2`
View SolutionIn Fig.6.60,
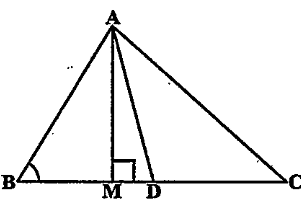 AD is a median of a triangle ABC and `AM_|_BC`.Prove that :(iii)`AC^2+AB^2=2AD^2+1/2BC^2`
AD is a median of a triangle ABC and `AM_|_BC`.Prove that :(iii)`AC^2+AB^2=2AD^2+1/2BC^2`
View SolutionIn Fig.6.61,
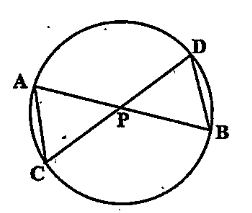 two chords AB and CD intersect each other at the point P.Prove that :(i)`triangleAPC~triangleDPB`
two chords AB and CD intersect each other at the point P.Prove that :(i)`triangleAPC~triangleDPB`
View SolutionIn Fig.6.61,
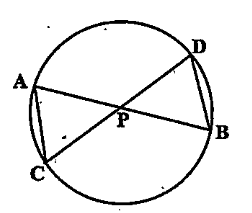 two chords AB and CD intersect each other at the point P.Prove that :(ii)PA.PB=CP.DP
two chords AB and CD intersect each other at the point P.Prove that :(ii)PA.PB=CP.DP
View SolutionIn Fig.6.62,
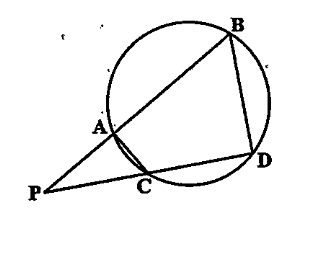 two chords AB and CD of a circle intersect each other at the point P(when produced)outside the circle.Prove that (i)`trianglePAC~trianglePDB`
two chords AB and CD of a circle intersect each other at the point P(when produced)outside the circle.Prove that (i)`trianglePAC~trianglePDB`
View SolutionIn Fig.6.62,
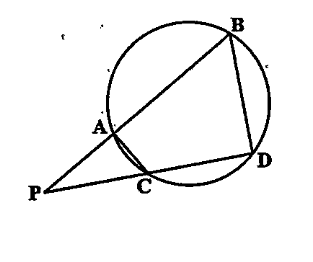 two chords AB and CD of a circle intersect each other at the point P(when produced)outside the circle.Prove that (ii)PA.PB=PC.PD
two chords AB and CD of a circle intersect each other at the point P(when produced)outside the circle.Prove that (ii)PA.PB=PC.PD
View SolutionState basic proportionality theorem.
View SolutionIn the adjoining figure,
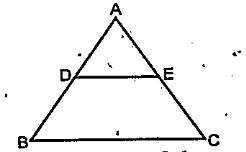 `DE||BC` and AD=1 cm,BD=2 cm.What is the ratio of the area of `triangleABC`to the area of `triangleADE`?
`DE||BC` and AD=1 cm,BD=2 cm.What is the ratio of the area of `triangleABC`to the area of `triangleADE`?
View SolutionThe areas of two similar triangles are `169cm^2 and 121cm^2`respectively.If the longest side of the larger triangle is 26 cm.what is the length of longest side of the smaller triangle.
View SolutionIf `triangle ABC and triangleDEF`are similar triangle such that`angleA=57^@ and angleE=73^@`,what is the measure of `angleF`?
View SolutionIf the altitude of two similar triangle are in the ratio 2:3 what is the ratio of their areas?
View SolutionState Pythagoras theorem.
View SolutionThe lengths of the diagonals of a rhombus are 30cm and 40cm.Find the side of the rhombus.
View SolutionIn an isosceles `triangleABC`if `AC=BC and AB^2=2AC^2` then what is the measure of `angleC`?
View SolutionWhat is the height of an equilateral triangle having each side 12 cm?
View SolutionSides of two similar triangle are in the ratio 4:9.Areas of these triangle are in the ratio
a)`2:3` b)`4:9` c)`81:16` d)`16:81`
View Solution`triangleABC~triangleDEF`such that ar`(triangleABC) =36cm^2and(triangleDEF)=49cm^2`.Then the ratio of their corresponding sides is
View Solution
EXERCISE questions and complete solutions for chapter TRIANGLES of R G PUBLICATION of Class 10