Complete Solutions to Exercise 7A of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| RS AGGARWAL | Exercise 7A |
| Number Of Questions | 12 |
| Academic Year | 2023-24 |
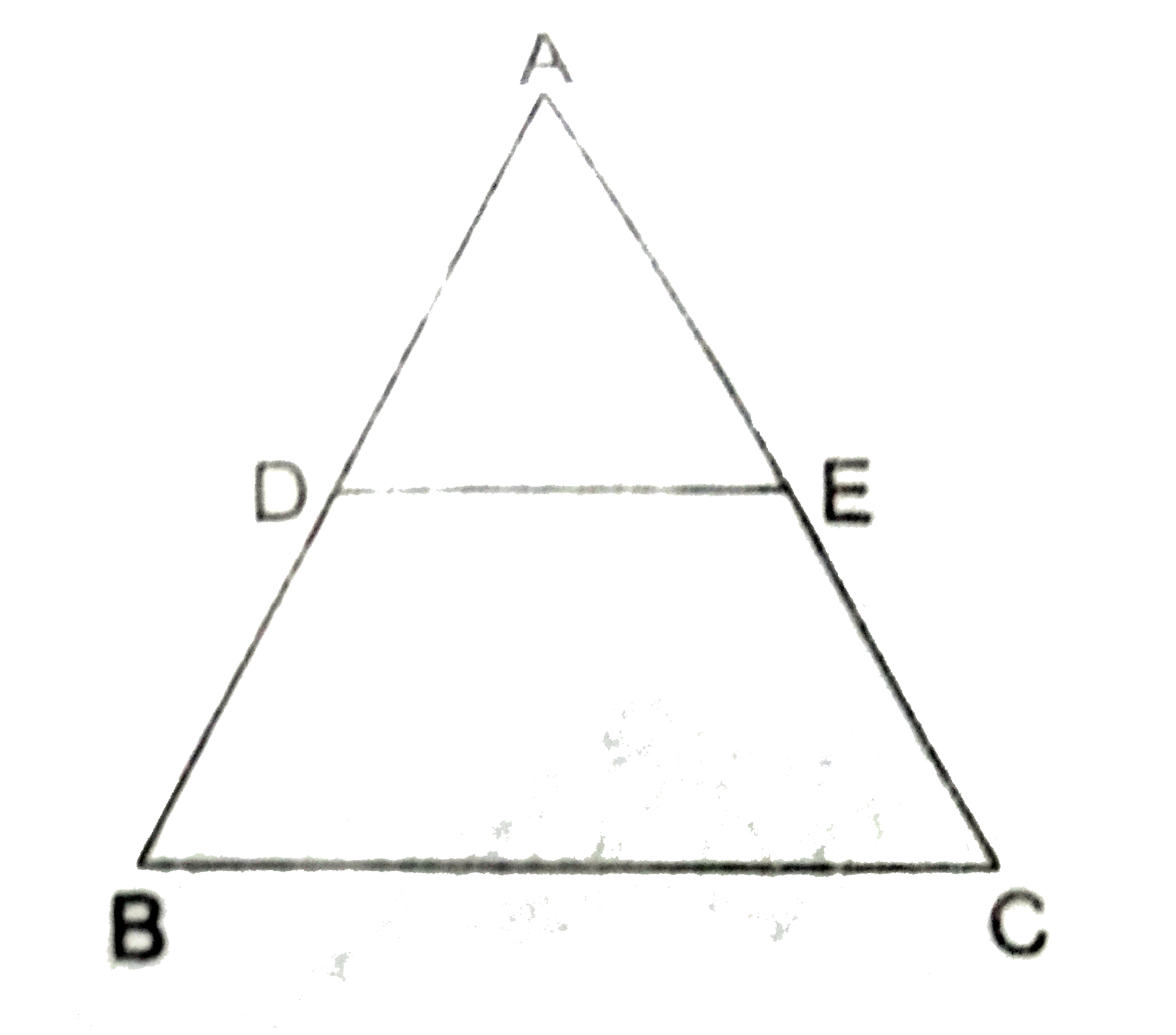
D and E are points on the sides AB and AC respectively of a `Delta ABC` such that `DE||BC`.
Find the value of x, when
(i) `AD =x cm, DB=(x-2) cm`,
`AE=(x+2) cm and EC =(x-1) cm`.
(ii) `AD=4 cm, DB =(x-4) cm, AE =8 cm`
and `EC=(3x-19) cm`.
`(iii) AD =(7x-4) cm, AE =(5x-2) cm, DB (3x+4) cm and EC= 3x cm`.
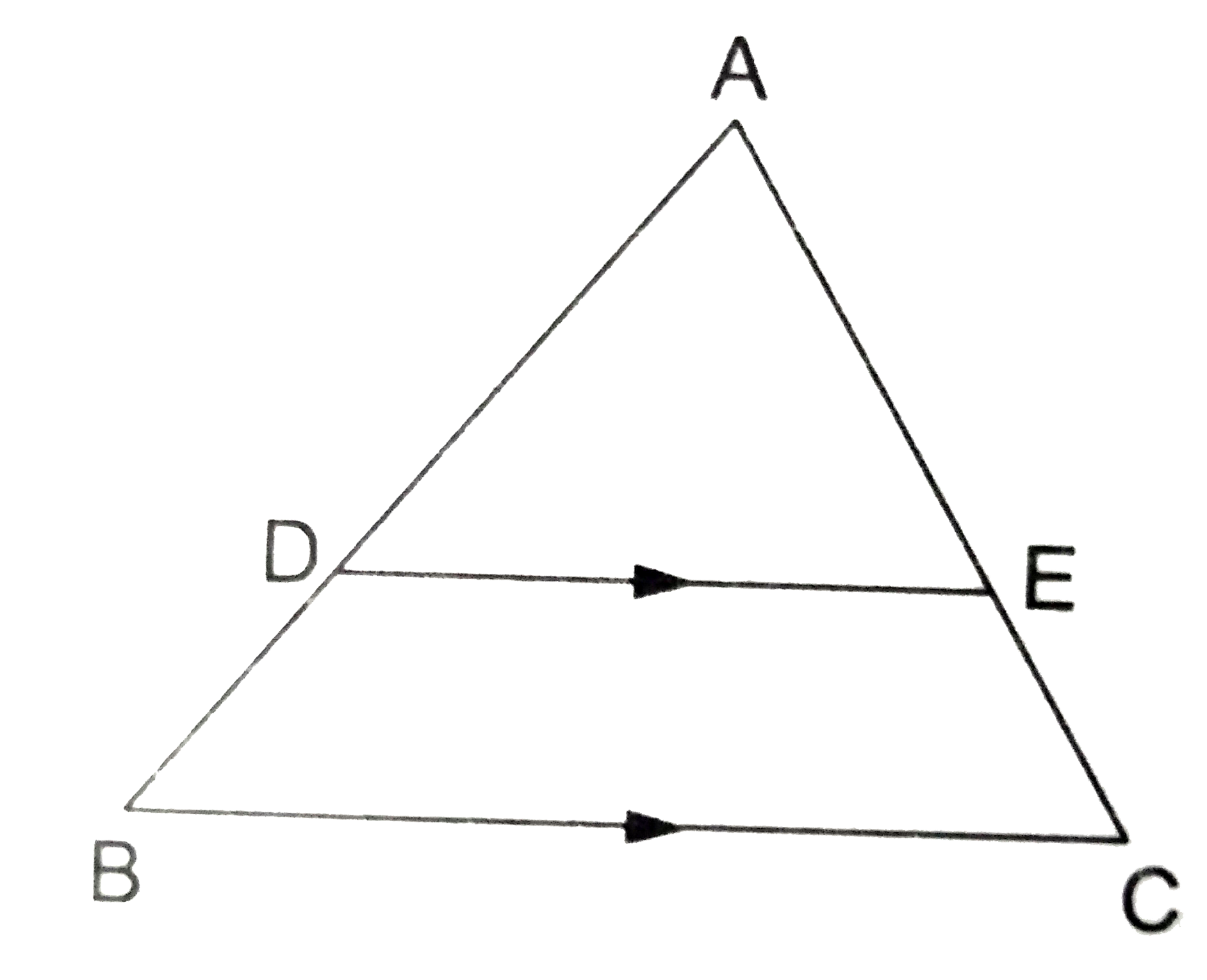
View SolutionD and E are points on the sides AB and AC respectively of `Delta ABC `. In each of the following cases, determine whetheer `DE||BC` or not. (i) `AD=5.7 cm, DB =9.5 cm, Ae =4.8 cm and EC=8 cm`. (ii) `AB=11.7 cm, AC =11.2 cm , AD= 6.5cm and AE =41.2 cm`, (iii) `AB=10.8 cm, AD=6.3 cm, AC=9.6 cm and EC=4 cm`. (iv) `AD=7.2 cm AE=6.4 cm. AB =12 cm and AC=10 cm`.
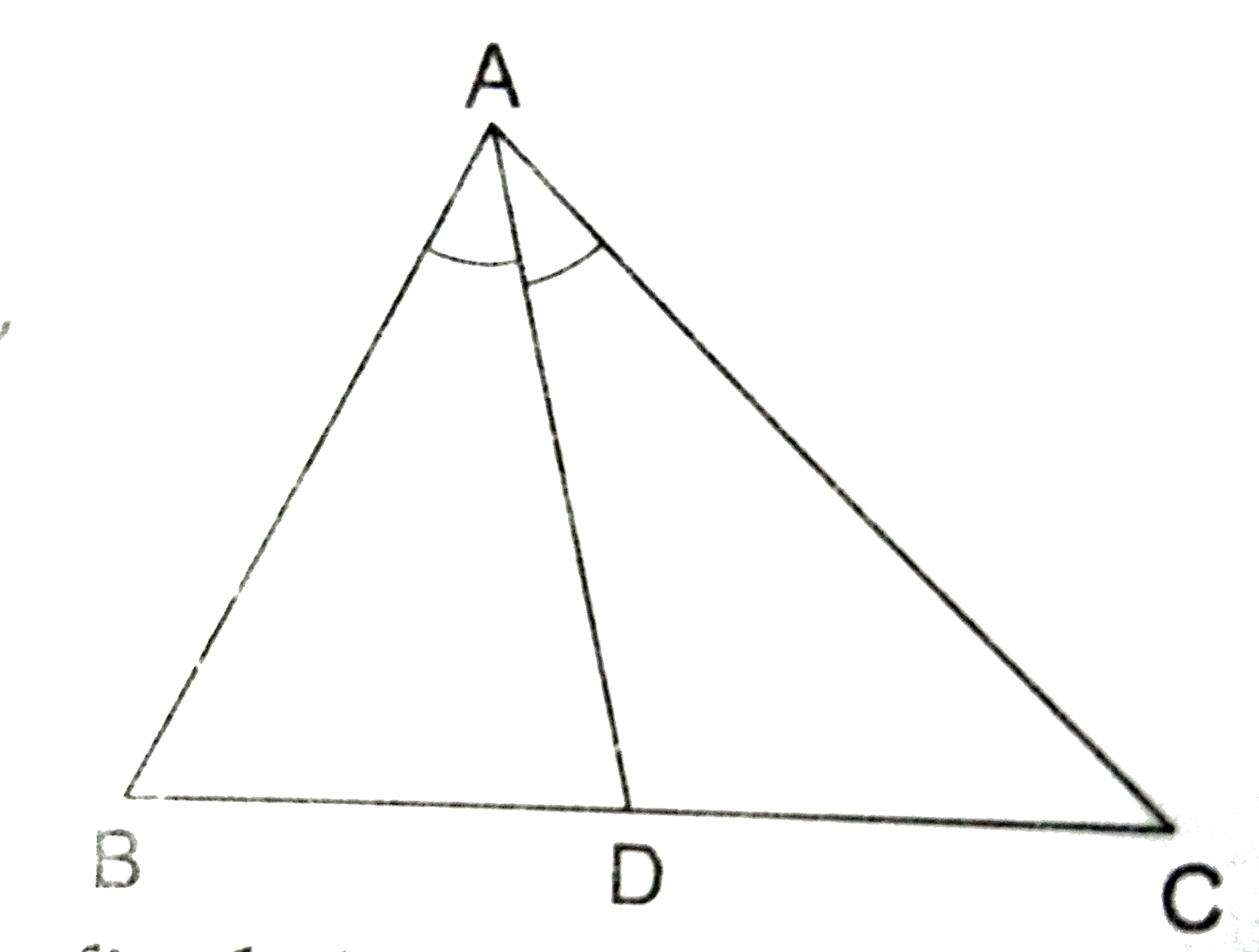
View SolutionIn a `Delta ABC, AD` is the bisector of `angle A`.
(i) If `AB=6.4 cm, AC=8 cm and BD=5.6 cm,` find DC.
(ii) If `AB=10 cm, AC=14 cm and BC=6 cm`, find BD and DC.
(iii) If `AB=5.6 cm, BD=3.2 cm, and BC=6 cm`, find AC.
(iv) If `AB=5.6 cm, AC=4 cm, and DC 3 cm`, find BC.
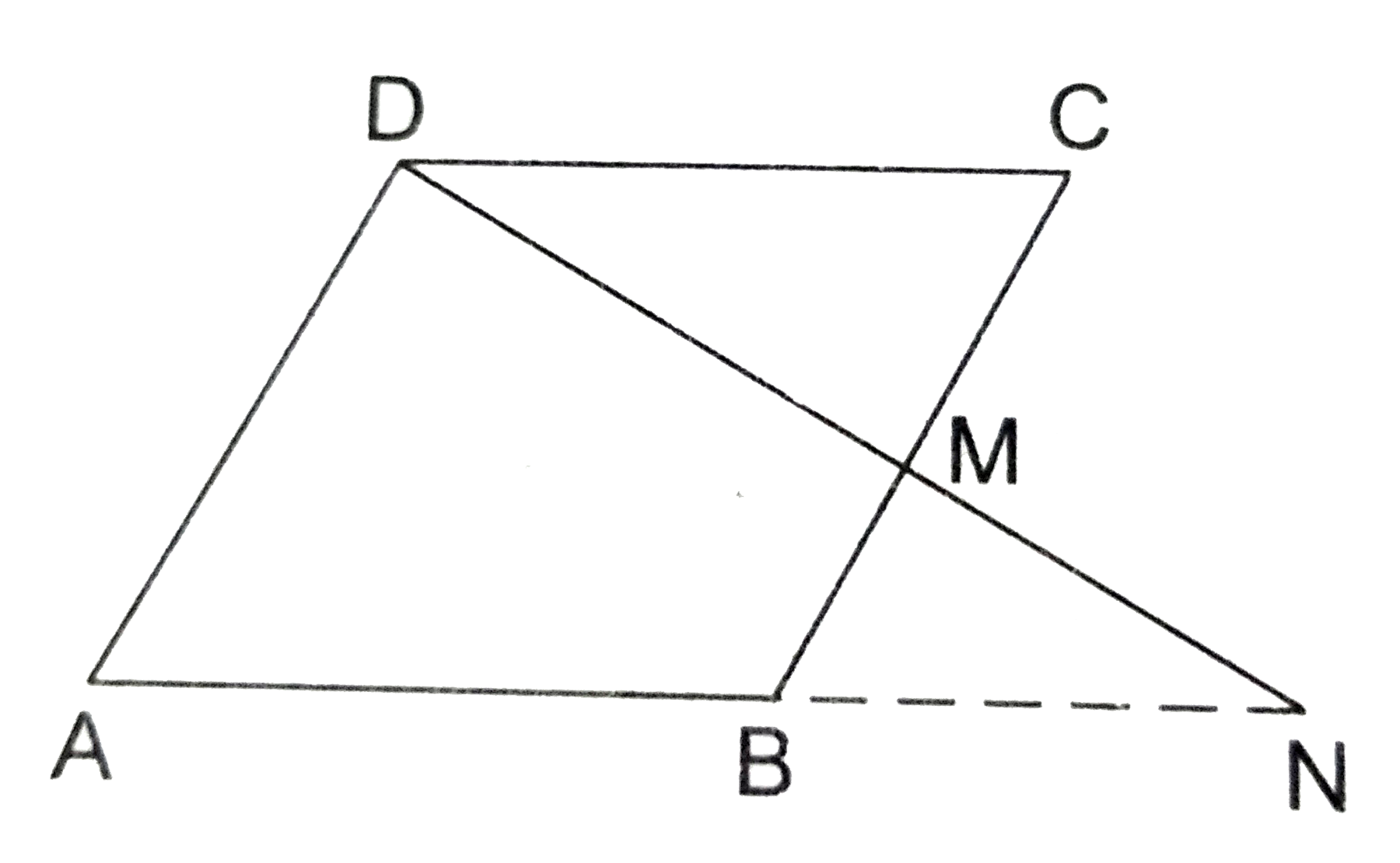
View SolutionM is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
` (i) (DM)/(MN)=(DC)/(BN)" " (ii) (DN)/(DM)=(AN)/(DC)`
View SolutionShow that the line segment which joins the midpooints of the oblique sides of a trapesium is parallel to the sides.
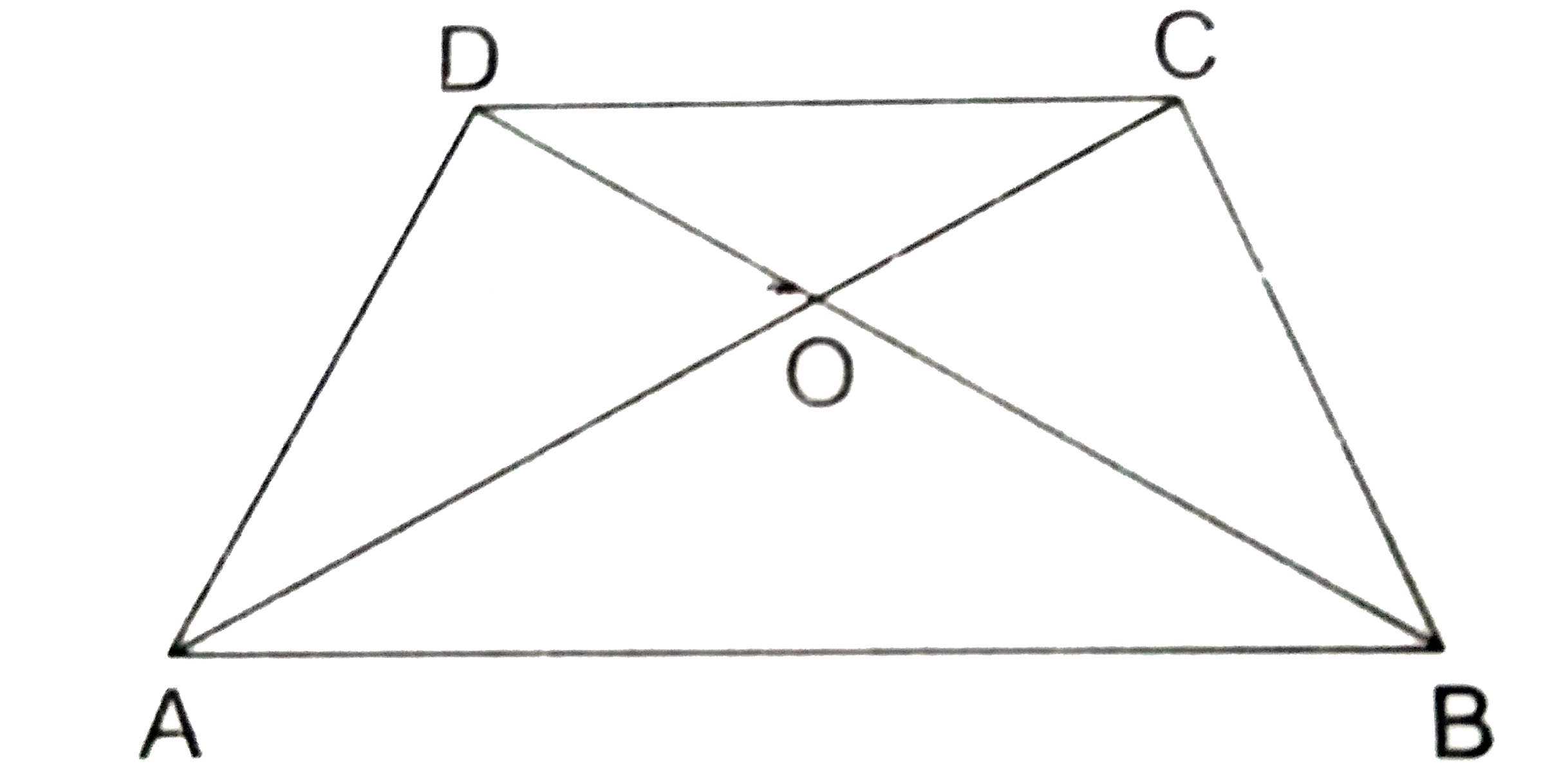
View SolutionIn the adjoining figure, ABCD is a trapezium in which `CD||AB` and its diagonals intersect at O. if `AO= (5x-7) cm, OC =(2x+1)cm, BO=(7x-5) cm and OD =(7x+1)cm`, find the value of x.
View SolutionIn `Delta ABC, M and N` are points on the sides AB and AC respectively such that `BM=CN`. If `angle A= angle C` then show that `MN||BC`.
View Solution`Delta ABC and Delta DBC` lie on the same side of BC, show in the figure. From a point on `BC.PQ||AB and PR||BD` are drawn, meeting AC at Q, and CD at R respectively. Prove that `QR||AD`.
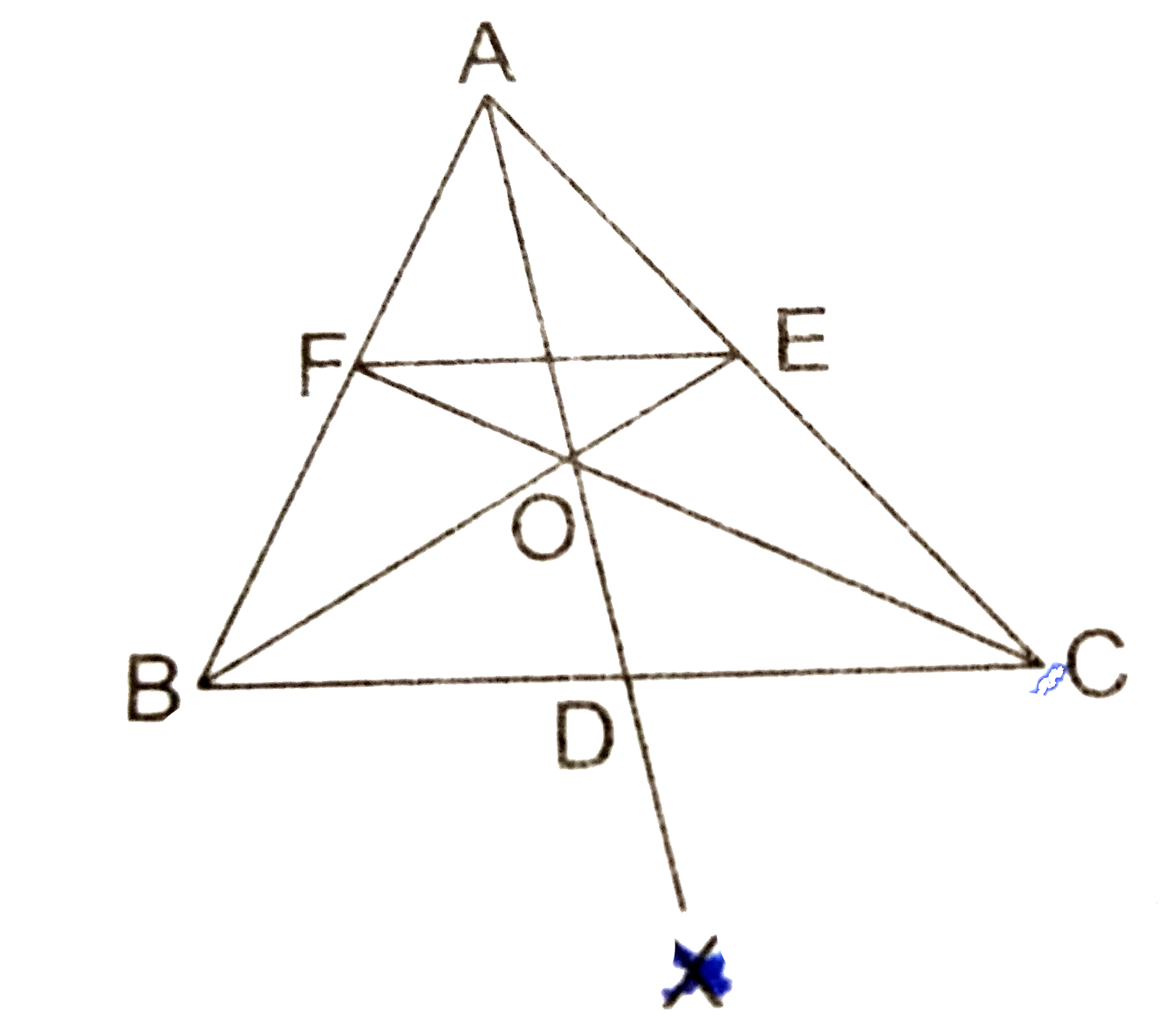
View SolutionIn the given figure, side BC of `Delta ABC` is bisected at D and O is any point AD.BO and CO produced meet AC and AB at E and F respectively, and AD is respectively, and AD is produced to X so that D is the midpoint of OX. Prove that `AO:AX=AF:AB` and show that `EF||BC`.
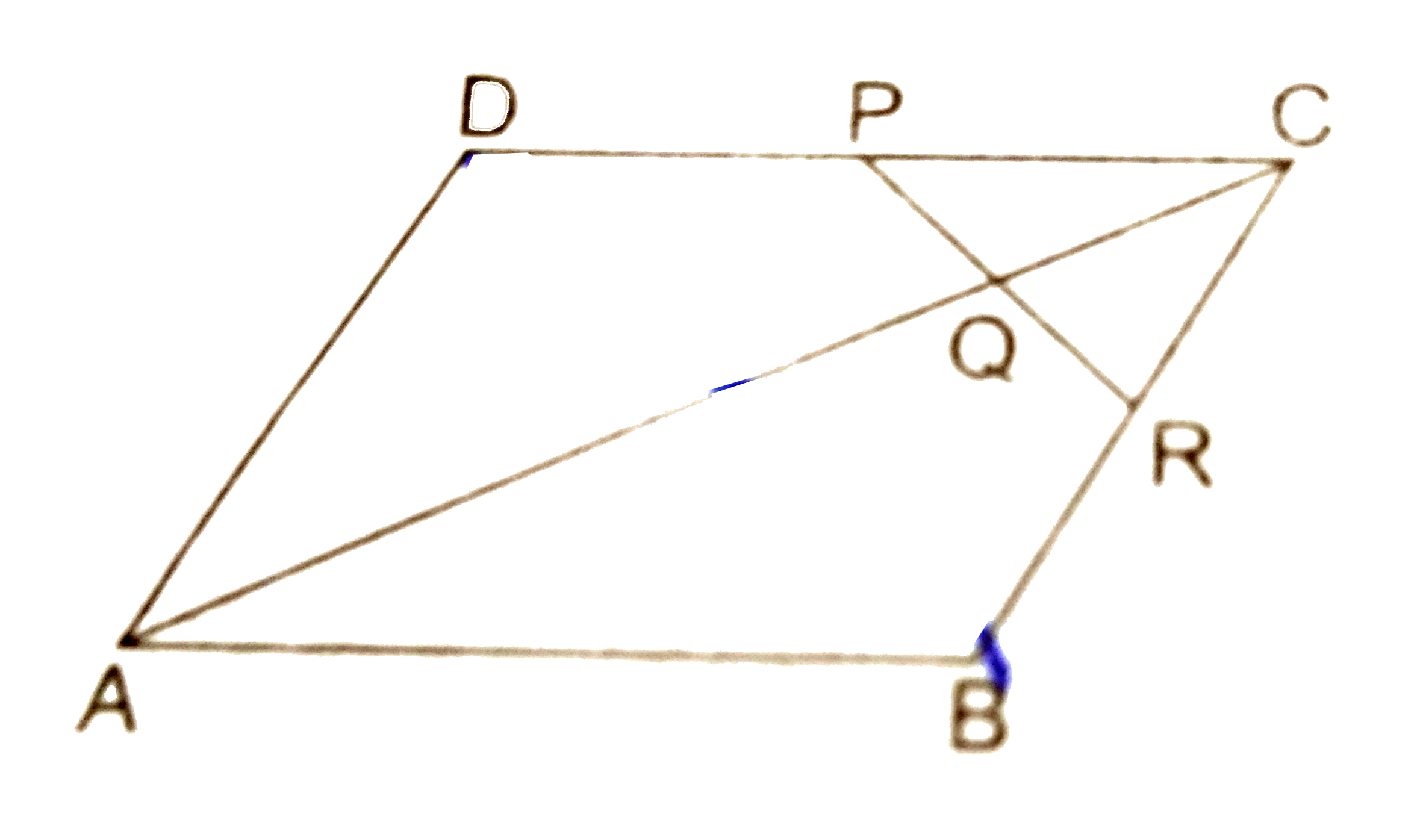
View SolutionABCD is a parallelogram in which P is the midpoint of DC and Q is a point on AC such that CQ `=(1)/(4) AC`. If PQ produced meets BC at R, prove that R is the midpoint of BC.
View SolutionIn the adjoining figure, ABC is a triangle in whcich AB=AC. If D and E are poitns on AB and AC respecrtively such that AD=AE, show that the points B,C,E and D are concyclic.
View SolutionIn `Delta ABC`, the bisector of `angle B` meets AC at D. A line `PQ||AC` meets AB,BC and BD at P,Q and R respectively. Show that `BPxxQR=BQxxPR`.
View Solution
Exercise 7A questions and complete solutions for chapter TRIANGLES of RS AGGARWAL MATHS (HINGLISH) of Class 10