Complete Solutions to Exercise 7D of chapter TRIANGLES of Class 10 book with complete answers and questions
| Class 10 | MATHS |
| Chapter | TRIANGLES |
| RS AGGARWAL | Exercise 7D |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
Find in each cash whether the sides of the triangle, as given below form a right triangle or not
(1) 9 cm, 12 cm and 15 cm (ii) 8 cm,15 cm and 17 cm
(iii) 7 cm, 24 cm and 25 cm
View SolutionA man goes 80 m due east and then 150 m due north. How far is he from the starting point?
View SolutionA man goes 10 m due south and then 24 n due west. How far is from the starting point ?
View SolutionA 13-m long ladder reaches a window of building 12 m above the ground. Determine the distance of the foot the ladder from the building.
View SolutionA ladder is placd in such a way that its foot is a distance of 15 m from a wall and its top reaches a window 20m abvoe the ground. Find the leng of the ladder .
View SolutionTwo poles of height `9`m and `14`m stand on a plane ground. If the distance between their feet is `12`m, find the distance between their tops.
View SolutionA guy wire attached to a vertical pole of height 18m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
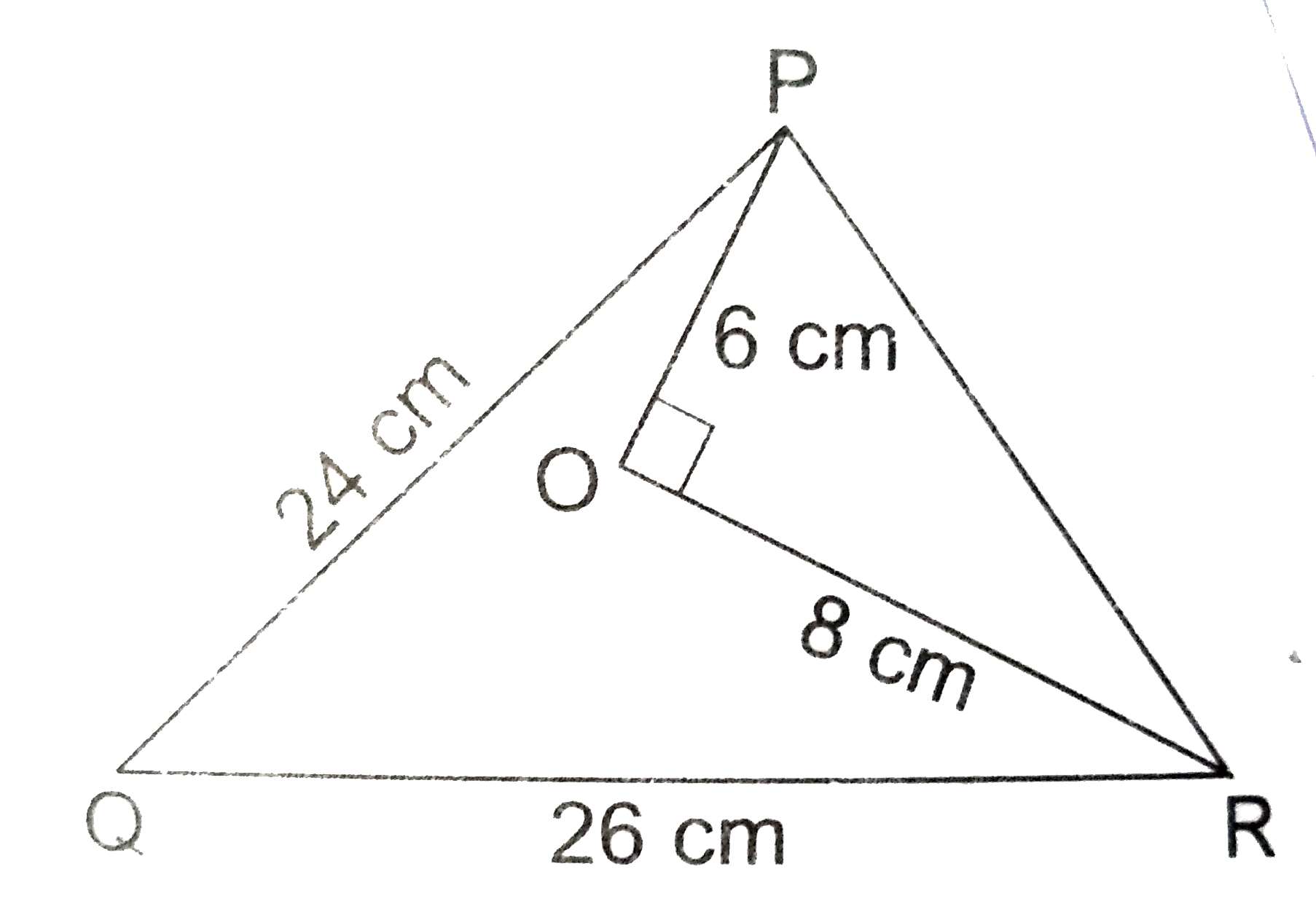
View SolutionIn the given figure, O is point inside a `Delta PQR` such that `angle POR=90^(@), OP=6 cm and OR=8 cm`. If `PQ=24cm and QR=26cm`, prove that `Delta PQR` is right angled.
View SolutionIn an isosceles triangle `A B C` , if `A B=A C=13` cm and the altitude from `A` on `B C` is 5 cm, find `B C` .
View SolutionFind the length of altitude AD of an isosceles `Delta ABC` in which `AB=AC=2a` units and BC=a units.
View Solution`Delta ABC ` is an equilateral triangle of side 2a units. Find each of its altitudes.
View SolutionFind the height of an equilateral triangle of side 12 cm
View SolutionFind the length of a diagonal of reactangle whose adjacent sides are 30 and 16 cm
View SolutionFind the length of each side of a rhombus whose diagonals are 24 cm and 10 m long.
View SolutionIn `Delta ABC , D` is the midpoint of BC and `AE bot BC`. If `AC gtAB`, show that `AB^(2)=AD^(2)-BC*DE+(1)/(4)BC^(2)`
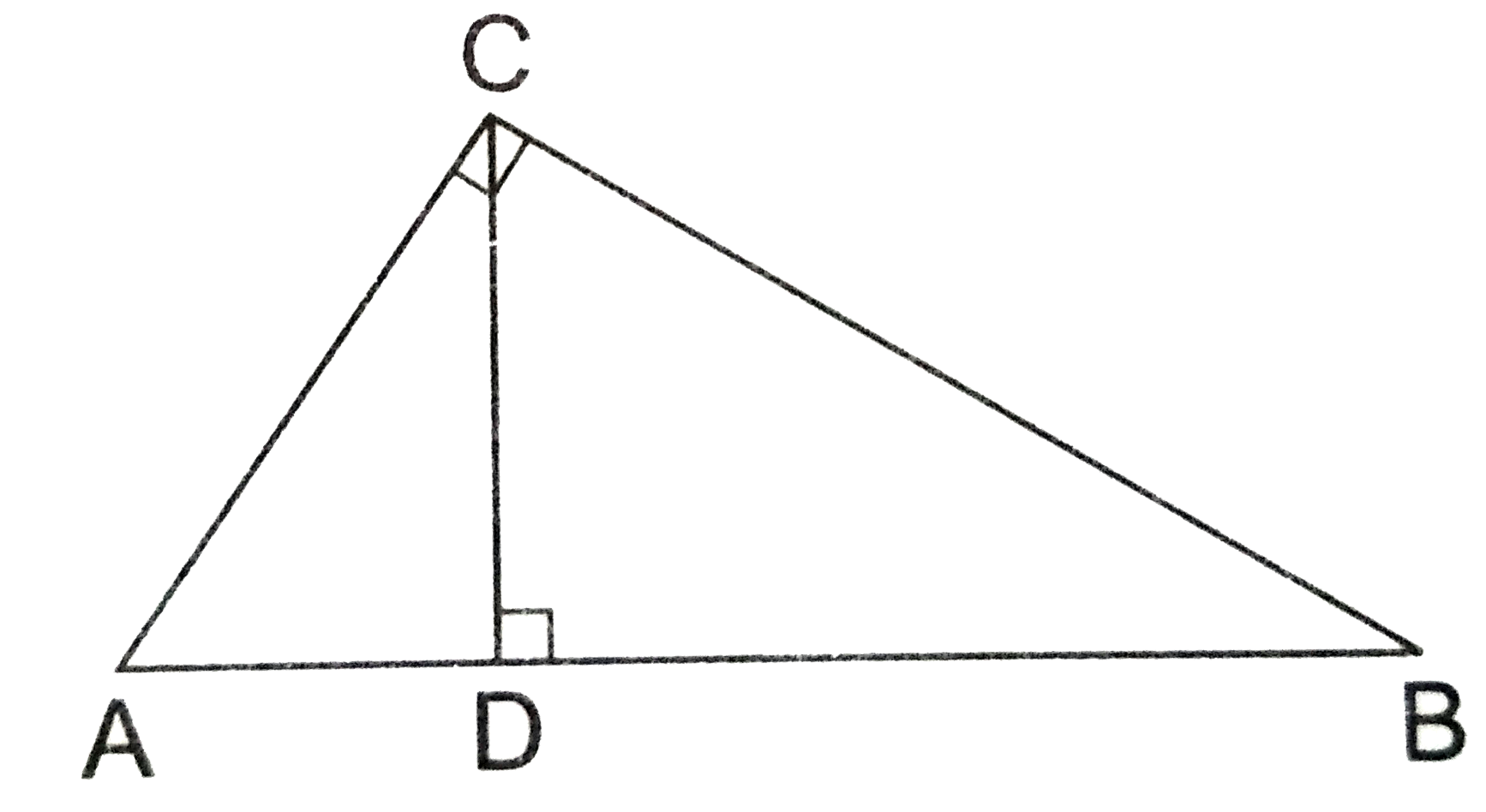
View SolutionIn the given figure `angleABC=90^(@) and CD bot AB`. Prove that `(BC^(2))/(AC^(2))=(BD)/(AD)`
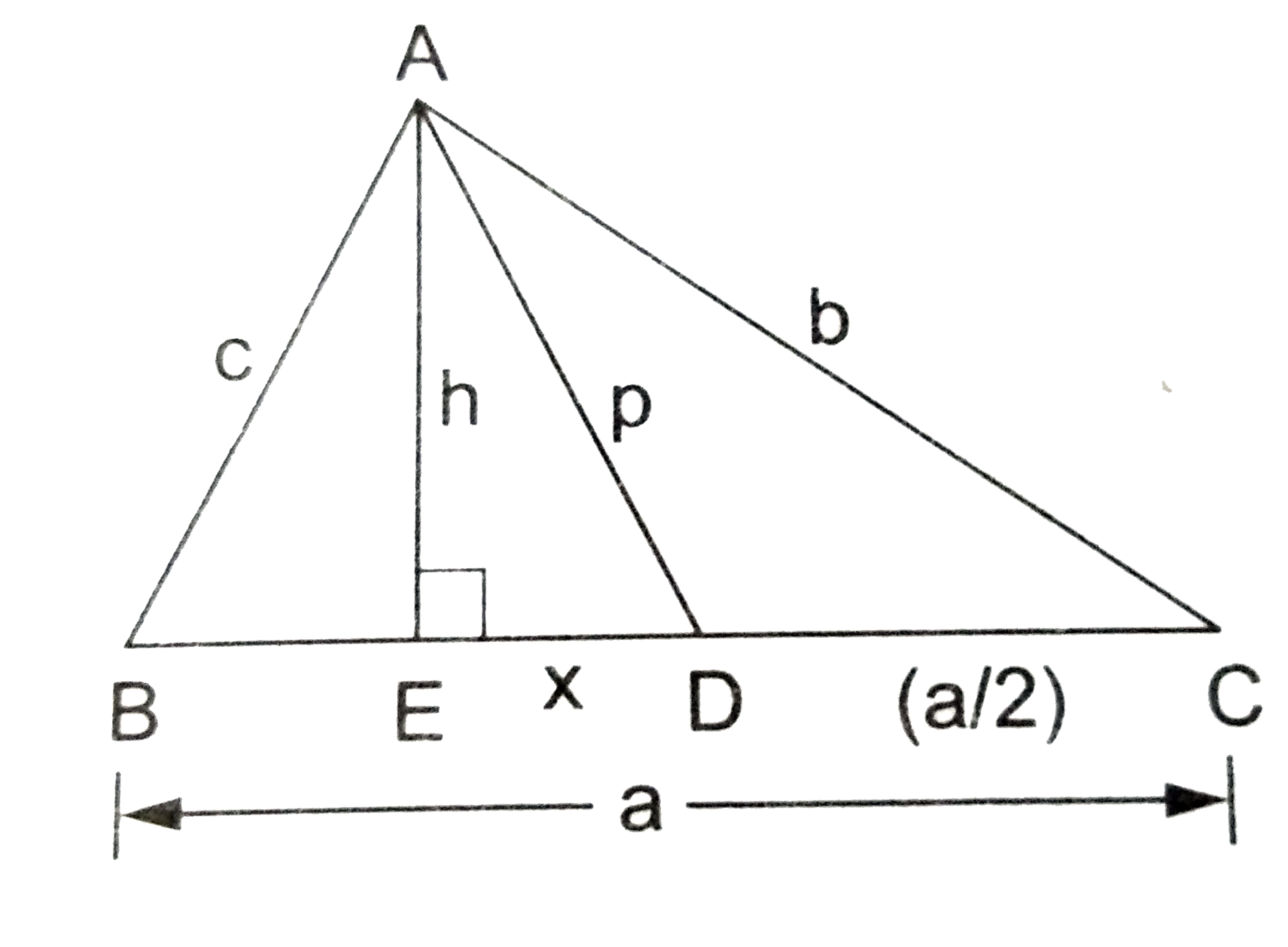
View SolutionIn the given figure, D is the midpoint of side BC and `AE bot BC`. If `BC=a, AC =b, AB= c, ED =x AD=p and AE =h` prove that
`(i) b^(2)=p^(2)+ax +(a^(2))/(4)`
(ii) `c^(2)=p^(2)-ax+(a^(2))/(4)`
(iii) `(b^(2)+c^(2))=2p^(2)+(1)/(2)a^(2)`
`(iv) (b^(2)-c^(2))=2ax`.
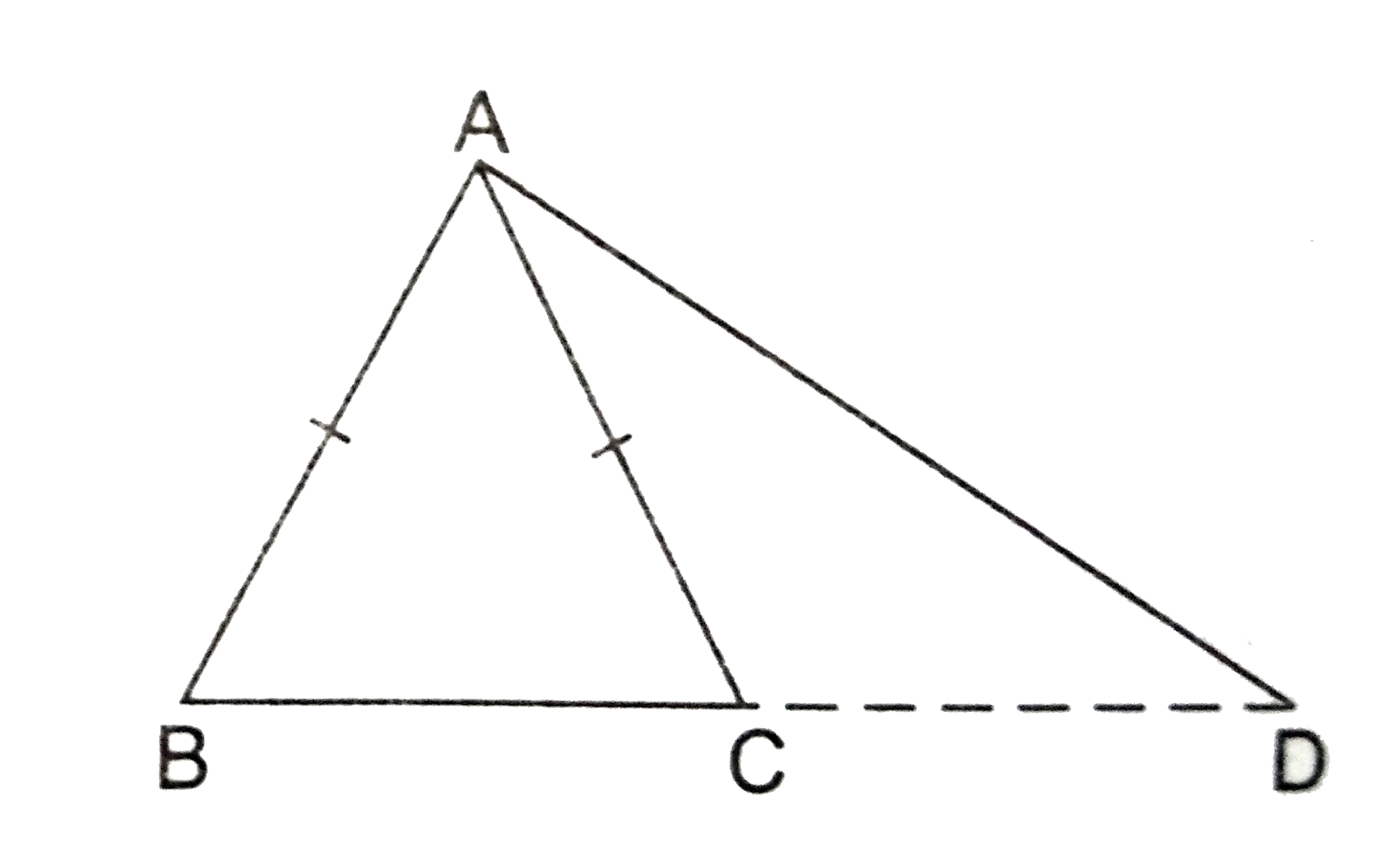
View SolutionIn `Delta ABC, AB= AC`. Side BC is produced to D. Prove that `(AD^(2)-AC^(2))=BD*CD`.
View SolutionABC is an isosceles triangle, right-angled at B. Similar trianles ACD and ABE are constructed on sides AC and AB. Find ratio between the areas of `Delta ABE and Delta ACD`.
View SolutionAn aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same tune, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. |How far apart will be the two planes after 1`1/2
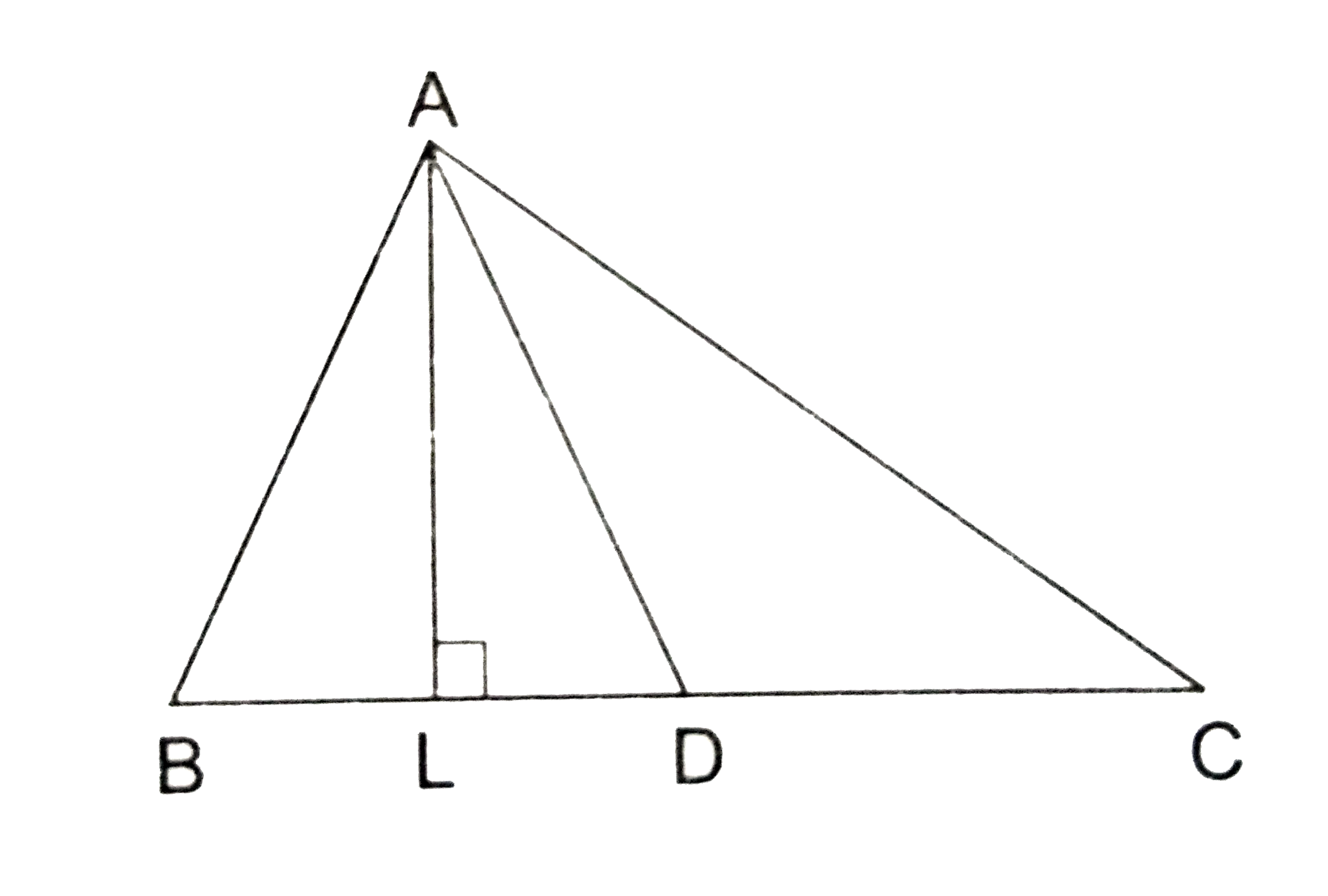
View SolutionIn `a Delta ABC, AD` is a median and `AL bot BC`.
Prove that
(a) `AC^(2)=AD^(2)+BC*DL+((BC)/(2))^(2)`
(b) `AB^(2)=AD^(2)-BC*DL+((BC)/(2))^(2)`
(c) `AC^(2)+AB^(2)=2AD^(2)=2AD^(2)+(1)/(2)BC^(2)`
View SolutionNazinia is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that h
View Solution
Exercise 7D questions and complete solutions for chapter TRIANGLES of RS AGGARWAL MATHS (HINGLISH) of Class 10