Complete Solutions to Gravitational Potential, Energyand Escape Velocity of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| A2Z | Gravitational Potential, Energyand Escape Velocity |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
There is no atomosphere on moon because
01:50View SolutionA projectile is launched from the surface of earth with a velocity less than the escape velocity. Its total mechanical energy is
03:33View SolutionThe intensity of gravitational field at a point situated at a distance of 8000km form the centre of the earth is `6//kg`. The gravitational potential at that point is -(in joule /kg)
02:27View SolutionA body of mass m kg starts falling from a point 2R above the earth's surface. Its kinetic energy when its has fallen to a point 'R' above the earth's surface [R Radius of earth M-mass of earth, G-gravitational constant]
03:46View SolutionThe escape velocity for a body projected vertically upwards from the surface of earth is 11km/s. If the body is projected at an angle of `45^@` with the vertical, the escape velocity will be
01:03View SolutionA body of mass m is situated at a distance `4R_(e)` above the earth's surface, where `R_(e)` is the radius of earth. How much minimum energy be given to the body so that may escape
03:20View SolutionAssuming earth as a uniform sphere of radius R, if we project a body along the smooth diametrical chute form the centre of earth with a speed v such that it will just reach the earth's surface then v is equal to :
04:55View SolutionIn the above question, escape speed from the centre of earth is :
03:22View SolutionLet the minimum external work done in shifting a particle from centre of earth to earth's surface be `W_(1)` and that from surface of earth to infinity be `W_(2)` . Then `(W_(1))/(W_(2))` is equal to
04:03View SolutionThe escape velocity form the centre of a unifrom ring of mass M and radius R is :
05:49View SolutionA shell of mass M and radius R has point mass m placed at a distance r from its centre. The gravitational potential energy U(r) vs r will be
02:31View SolutionA projectile is launched from the surface of earth with a velocity less than the escape velocity. Its total mechanical energy is
03:33View SolutionThe gravitational potential energy of body of mass 'm' at the earth's surface `mgR_(e)`. Its gravitational potential energy at a height `R_(e)` fromt the earth's surface will be (here `R_(e)` is the radius of the earth)
03:19View SolutionA rocket is launched vertically from the surface of earth with an initial velocity `v`. How far above the surface of earth it will go? Neglect the air resistance.
02:57View SolutionA body of mass m kg starts falling from a point 2R above the earth's surface. Its kinetic energy when its has fallen to a point 'R' above the earth's surface [R-Radius of earth M-mass of earth, G-gravitational constant]
03:46View SolutionMaximum height reached by a rocket fired with a speed equal to 50% of the escape velocity from earth's surface is:
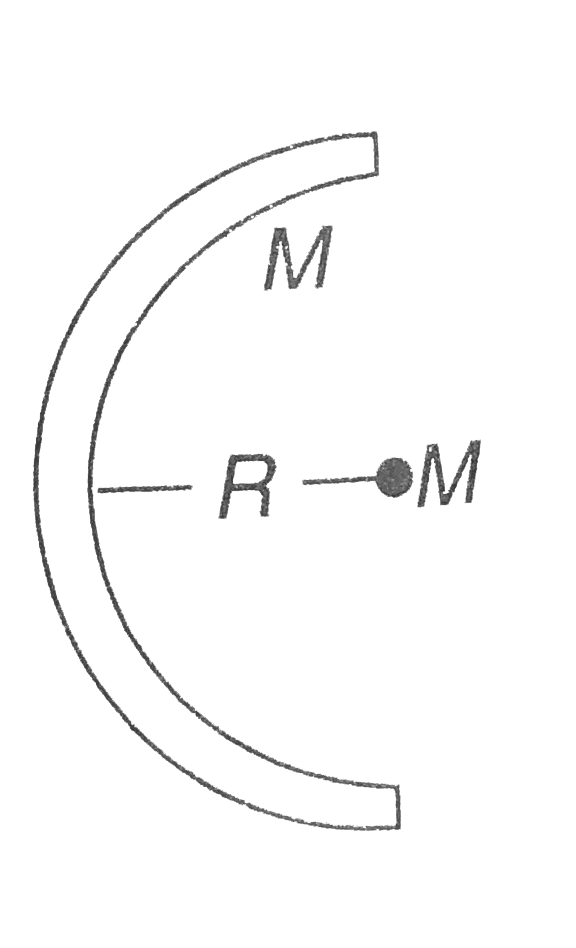
05:13View SolutionThe potential energy of interaction between the semi-circular ring of mass M and radius R, and the particle of mass M placed at the centre of curvature of the semi-circular arc is:
 05:15View Solution
05:15View SolutionTwo oppositely rotating satellities of same are launched in the same orbit round the earth. The collide idealistically. What is the ratio of gravitational potential energy before and after collistion?
04:46View SolutionA body of mass `m` is lifted up from the surface of earth to a height three times the radius of the earth `R`. The change in potential energy of the body is
02:50View SolutionFour particles each of mass `m` are kept at the four vertices of a square of side 'a' . Find gravitational potential energy of this system.
04:16View SolutionFour particles each of mass m are placed at the vertices of a square of side `l`. the potential at the centre of square is
04:00View SolutionThe change in the gravitational potential energy when a body of a mass `m` is raised to a height `nR` above the surface of the earth is (here `R` is the radius of the earth)
03:31View SolutionA particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
02:08View SolutionTwo spheres each of mass `M` and radius `R` are separated by a distance of `r`. The gravitational potential at the midpoint of the line joining the centres of the spheres is
02:21View SolutionThe mass of the earth is `6xx10^(24)kg` and that of the moon is `7.4xx10^(22)kg`. The potential energy of the system is `-7.79xx10^(28)J`. The mean distance between the earth and moon is `(G=6.67xx10^(-11)Nm^(2)kg^(-2))`
02:59View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance `a/2` from the centre.
05:01View SolutionThe escape velocity of a body form the earth depends on
(i) the mass of the body.
(ii) the location from where it is projected.
(iii) the direction of projection.
(iv) the height of the location form where the body is launched.01:46View SolutionThe escapoe speed of a body on the earth's surface is `11.2kms^(-1)`. A body is projected with thrice of this speed. The speed of the body when it escape the gravitational pull of earth is
03:54View SolutionThe escape velocity for a body of mass `1kg` from the earth surface is `11.2kms^(-1)`. The escape velocity for a body of mass `100kg` would be
01:41View SolutionThe mass of a planet is six times that of the earth. The radius of the planet is twice that of the earth. It's the escape velocity from the earth is `v`, then the escape velocity from the planet is:
01:57View SolutionIf `v_(e)` is escape velocity and `v_(0)`, is orbital velocity of satellite for orbit close to the earth's surface. Then are related by
01:01View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
03:07View Solution
Gravitational Potential, Energyand Escape Velocity questions and complete solutions for chapter GRAVITATION of A2Z PHYSICS (HINGLISH) of Class 11
