Complete Solutions to Problems Based On Mixed Concepts of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| A2Z | Problems Based On Mixed Concepts |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
A body is fired with a velocity of magnitude `sqrt(gR) lt Vsqrt(2gR)` at an angle of `30^(@)` with the radius vector of earth. If at the highest point the speed of the body is `V//4`, the maximum height attained by the body is equal to:
05:48View SolutionThe gravitational field intensity at a point `10,000km` from the centre of the earth is `4.8Nkg^(-1)`. The gravitational potential at that point is
02:17View SolutionA small body of superdense material, whose mass is twice the mass of the earth but whose size is very small compared to the size of the earth, starts form rest at a height `H lt lt R` above the earth's surface, and reaches the earth's surface in time `t`. then `t` is equal to
04:37View SolutionThe density of the core a planet is `rho_(1)` and that of the outer shell is `rho_(2)`. The radii of the core and that of the planet are `R` and `2R` respectively. The acceleration due to gravity at the surface of the planet is same as at a depth `R`. Find the ratio of `(rho_(1))/(rho_(2))`
 03:48View Solution
03:48View SolutionWork done by an external agent in bringing three particles each of mass `m` at the vertices of an equilateral triangle of length `l` is
02:52View SolutionThe ratio of KE of a planet at the points `1` and `2` is :
 02:47View Solution
02:47View SolutionIf radius of the earth contracts to half of its present value without change in its mass, what will be the new duration of the day?
03:19View SolutionFind the escape velocity of particle of mass `m` which is situated at a radial distance `r` (from centre of earth) above the earth's surface. `M` is the mass earth.
02:48View SolutionIf a particles of mass `m` is projected with minimum velocity form the surface of a star with kinetic energy `(K_(1)GMm)/a` and potential energy at surface of the star `(K_(2)GMm)/a` towards the star of same mass `m` and radius `a` (`K_(1)` and `K_(2)` are constant) to reach the other star. Find the distance between the centre of the two stars:
06:24View SolutionThe mass of a satellite is `M//81` and radius is `R//4` where `M` and `R` are the mass and radius of the planet. The distance between the surfaces of planet and its satellite will be atleast greter than:
05:03View SolutionThe orbital velocity of a satellite at point `B` with radius `r_(B)` and `n`. The radius of a point `A` is `r_(A)`. If the orbit is increased in radial distance so that `r_(A)` becomes `.12r_(A)` find the orbital velocity at `(1.2 r_(A))`:
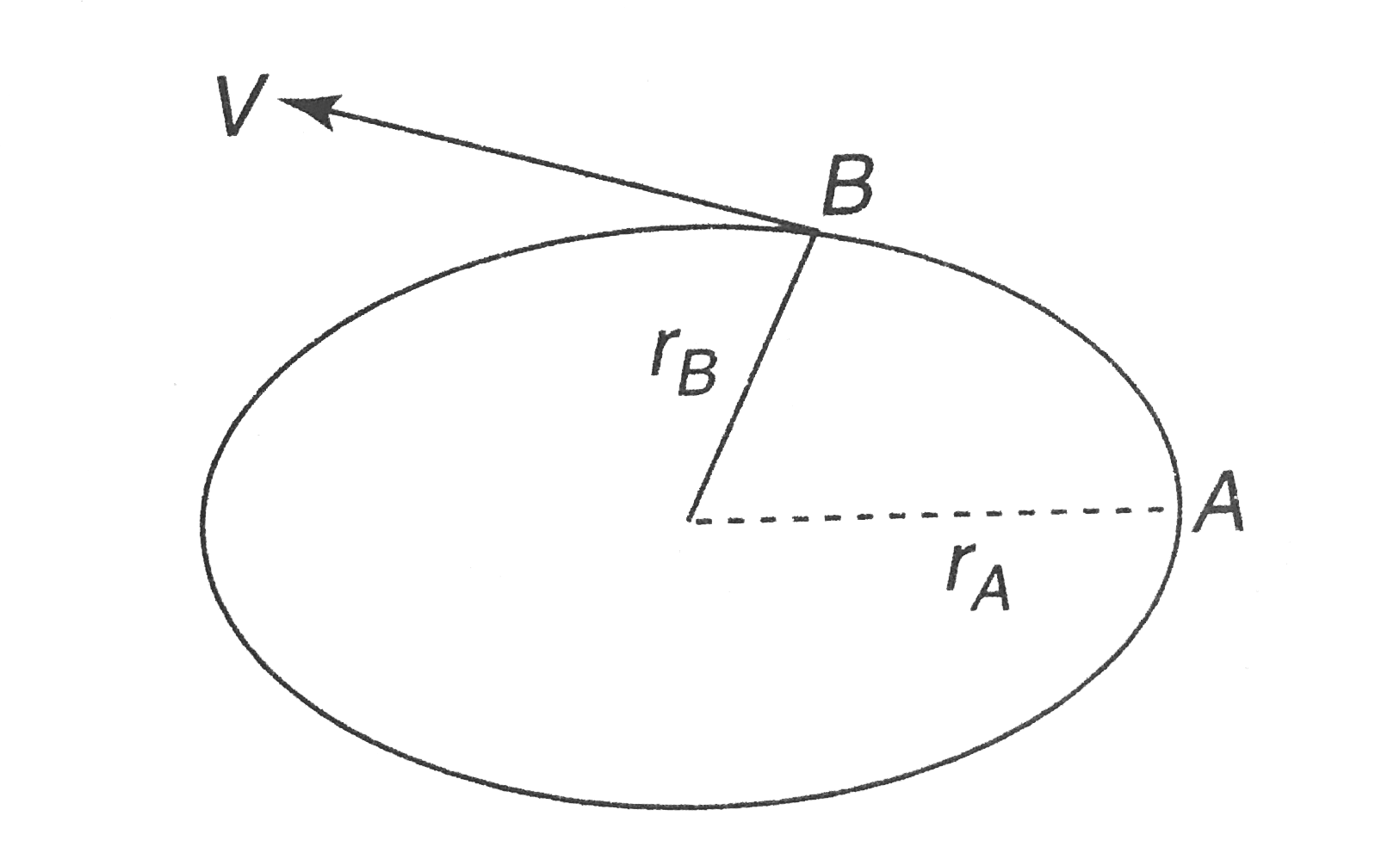 04:48View Solution
04:48View SolutionAn asteroid of mass `m` is approaching earth, initially at a distance `10R_(E)` with speed `v_(i)`. It hits earth with a speed `v_(f)` (`R_(E)` and `M_(E)` are radius and mass of earth),. Then
03:20View SolutionA projectile rises upto a maximum height of `R//(1-K^(2))` where `K` is a constant and `R` is the radius of earth. If the velocity of projectile with which it should be fired upwards form the surface of the earth to reach this height is equal to the product of a coeffiecient and escape velocity then this coeffiecient is equal to:
05:32View SolutionA particle is projected from the surface of one star towards other star of same radius `a` and mass with such a minimum velocity `Ksqrt((GM)/a)`, so that it is attracted towards other star. Find the value of `K` if two stars are `2r` distance apart:
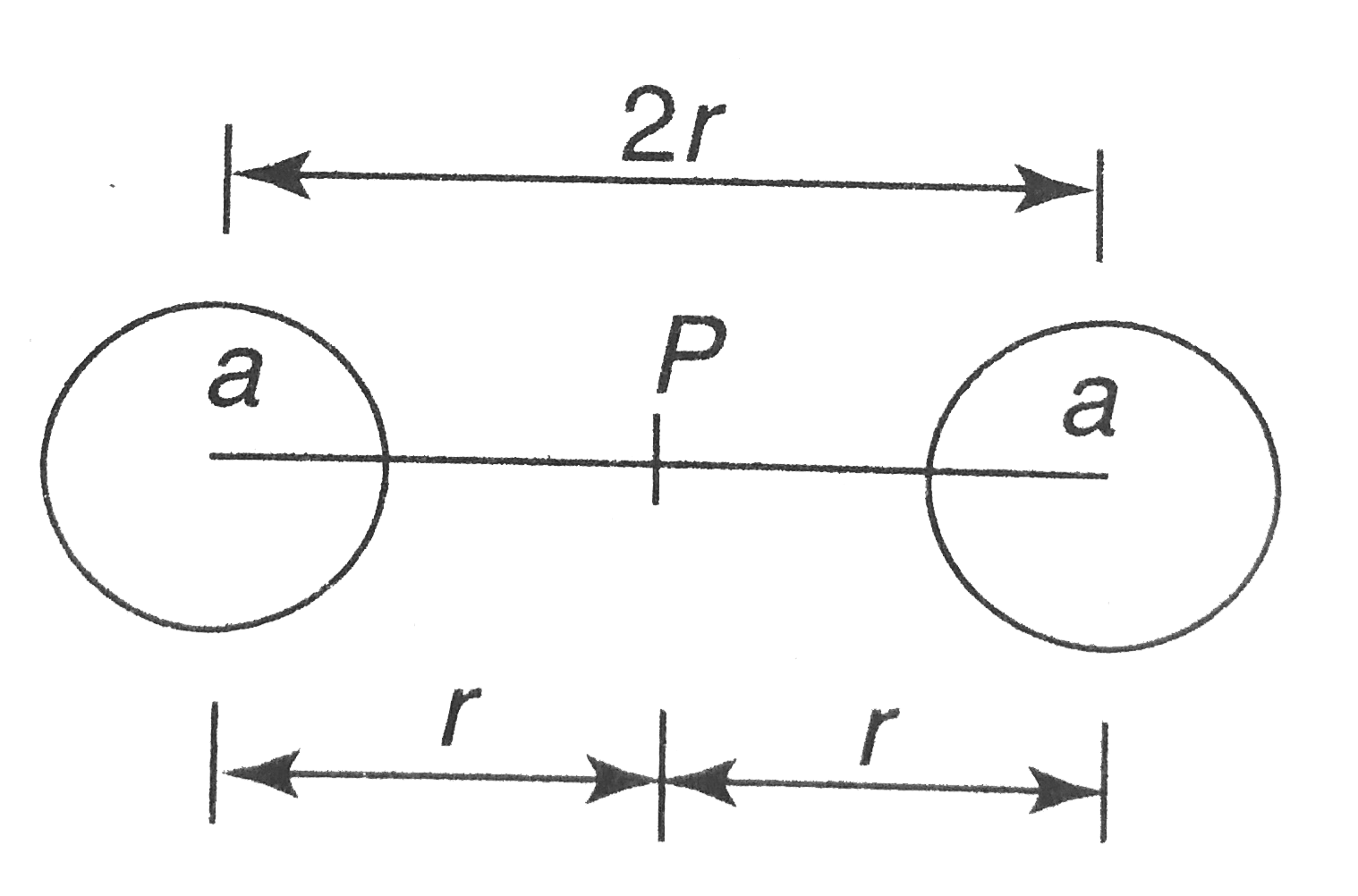 08:12View Solution
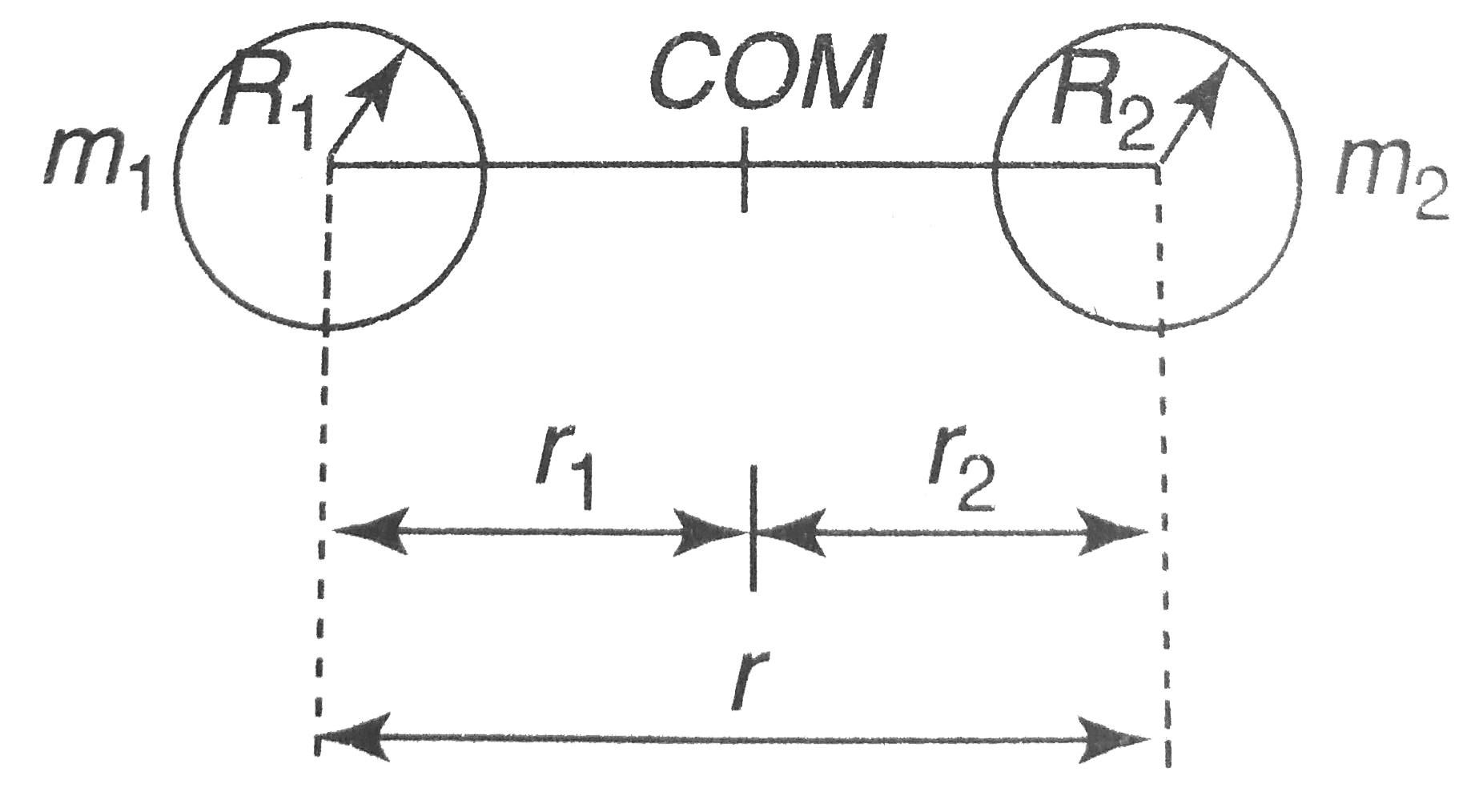
08:12View SolutionTwo stars of mass `m_(1)` and `m_(2)` are parts of a binary star system. The radii of their orbits are `r_(1)` and `r_(2)` respectivey, measured from the centre of mass of the system. The magnitude of gravitational force `m_(1)` exerts on `m_(2)` is
02:03View SolutionBinary stars of comparable masses rotates under the influence of each other's gravity at a distance `[(2G)/(omega^(2))]^(1//3)` where `omega` is the angular velocity of each of the system. If difference between the masses of two stars is `6` units. Find the ratio of the masses of smaller to bigger star.
 05:50View Solution
05:50View SolutionThe ratio of cube of circumferences of the orbit of a satellite to the volume of the earth is `6xx10^(10)(g//R)`, where `g` is the acceleration of gravity. Find the time period of satellite (in secods). `R` is the radius of earth
05:29View SolutionTwo planets revolve with same angular velocity about a star. The radius of orbit of outer planet is twice the radius of orbit of the inner planet. If `T` is time period of the revolution of outer planet, find the time in which inner planet will fall into the star. If it was suddenly stopped.
View SolutionWhat would be the projections velocity of a satellite so that intersteller (interspace with no gravitation) velocity of the satellite becomes the orbital velocity when it is in the orbit at height of `10R` from earth's surface, where `R` is the radius of the earth?
04:05View SolutionA satellite in equatorial plane is rotating in the direction of earth's rotation with time interval between its two consecutive appearence over head of an observer as time period of rotation of the earth, `T_(E)`. What is the time period of the satellite?
03:49View SolutionA satellite is orbiting with areal velocity `v_(a)`. At what height form the surface of the earth, it is rotating, if the radius of earth is `R`?
03:35View SolutionThe magnitude of the gravitational field at distance `r_(1)` and `r_(2)` from the centre of a uniform sphere of radius `R` and mass `M` are `F_(1)` and `F_(2)` respectively. Then:
03:35View SolutionA spherical planet has uniform density `pi/2xx10^(4)kg//m^(3)`. Find out the minimum period for a satellite in a circular orbit around it in seconds (Use `G=20/3xx10^(-11) (N-m^(2))/(kg^(2))`).
04:51View SolutionA particle is projected from point `A`, that is at a distance `4R` form the centre of the earth, with speed `V_(1)` in a direction making `30^(@)` with the line joining the centre of the earth and point `A`, as shown. Consider gravitational interaction only between thesetwo. (Use `(GM)/R=6.4xx10^(7) m^(2)//s^(2)`). The speed `V_(1)` if particle pasess grazing the surface of the earth is
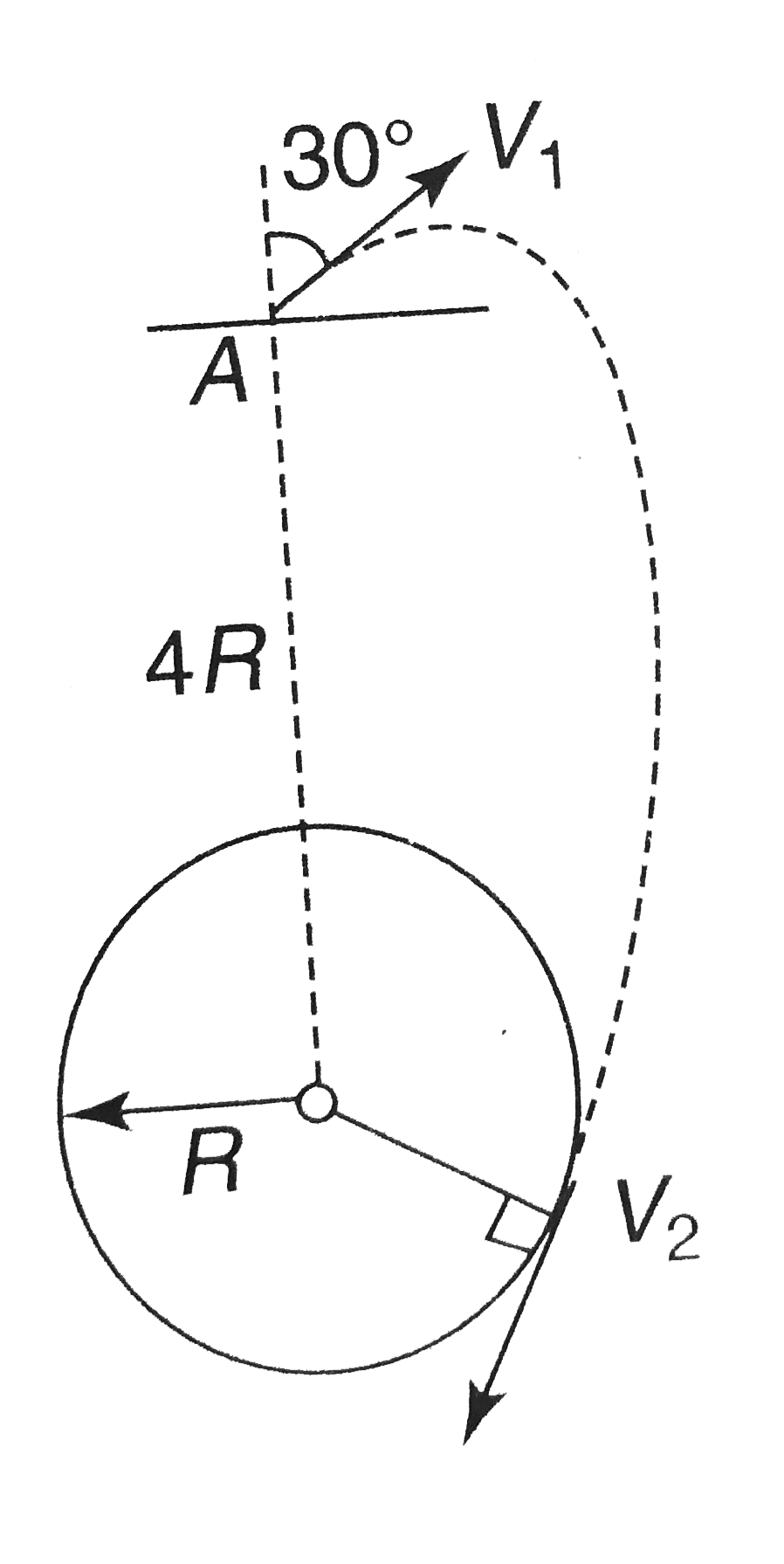 06:48View Solution
06:48View SolutionThree identical stars, each of mass `M`, from an equilateral triangle (stars are positioned at the corners) that rotates around the centre of the triangle. The system is isolated and edge length of the triangle is `L`. The amount of work done, that is required ot dismantle the system, is:
09:15View SolutionA satellite can be in a geostationary orbit around earth in an orbit of radius `r`. If the angular velocity of earth about its axis doubles, a satellite can now be in a geostationary orbit aroun earth radius
03:03View SolutionThe density of a newly discovered planet is twice that of earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the earth. If the radius of the earth is `R`, the radius of the planet would be
03:20View SolutionImagine a new planet having the same density as that of earth but `3` times bigger than the earth in size. If the acceleration due to gravity on the surface of earth is `g` and that on the new plane is `g` , then :
03:21View SolutionA cavity of radius `R//2` is made inside a solid sphere of radius `R`. The centre of the cavity is located at a distance `R//2` from the centre of the sphere. The gravitational force on a particle of a mass `'m'` at a distance `R//2` from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here `g=GM//R^(2)`, where `M` is the mass of the solid sphere]
08:25View Solution
Problems Based On Mixed Concepts questions and complete solutions for chapter GRAVITATION of A2Z PHYSICS (HINGLISH) of Class 11
