Complete Solutions to Vibration Of String of chapter WAVES AND ACOUSTICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WAVES AND ACOUSTICS |
| A2Z | Vibration Of String |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
A tuning fork vibrating with a sonometer having 20 cm wire produces 5 beats per second. The beat frequency does not change if the length of the wire is changed to 21 cm. The frequency of the tuning fork (in Hertz) must be
03:30View SolutionIn order to double the frequency of the fundamental note emitted by a stretched string, the length is reduced to `(3)/(4)`th of the original length and the tension is changed. The factor by which the tension is to be changed is
01:58View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N. Then speed of a wave on the string is
00:51View SolutionA second harmonic has to be generated in a string of length l stretched between two rigid supports. The point where the string has to be plucked and touched are
01:59View SolutionTwo wires are fixed in a sanometer. Their tension are in the ratio `8:1` The lengths are in the ratio `36:35` The diameter are in the ratio `4:1` Densities of the materials are in the ratio `1:2` if the lower frequency in the setting is `360Hz`. The beat frequency when the two wires are sounded together is
07:03View SolutionA string is rigidly tied at two ends and its equation of vibration is given by `y=sin2pix.cos2pit`. Then minimum length of string is
01:24View SolutionFundamental frequency of sonometer wire is `n`. If the length, tension and diameter of wire are tripled. The new fundamental frequency is
02:36View SolutionA string of length 2 m is fixed at both ends. If this string vibrates in its fourth normal mode with a frequency of 500 Hz then the waves wouldf travel on it is with a velocity of
01:38View SolutionFour wires of identical lengths, diameters and materials are stretched on a sonometer box. The ratio of their tension `1:4:9:16`. The ratio of their fundamental frequencies is
01:39View SolutionA guitar string of length L has a fundamental frequency. Where should it be pressed to produced another fundamental frequency. If the two fundamental frequenccis is f?
01:12View SolutionThe first overtone of a stretched string of given length is 320 Hz. The first harmonic is
01:03View SolutionA wire having a linear mass density `5.0xx10^(3) kg//m` is stretched between two rigid supports with tension of 450 N. The wire resonates at a frequency of `420 Hz`. The next higher frequency at which the same wire resonates is ` 480 N`. The length of the wire is
01:29View SolutionA wire of length l having tension T and radius `r` vibrates with fundamental frequency `f`. Another wire of the same metal with length `2l` having tension `2T` and radius `2r` will vibrate with fundamental frequency :
01:19View SolutionThe equation for the vibration of a string fixed at both ends vibrating in its third harmonic is given by `y=2cm sin[(0.6cm^-1)x]cos[(500pis^-1)t]`. The length of the string is
01:54View SolutionA violin string oscillating in its fundamental mode, generates a sound wave with wavelength `lambda`. To generate a sound wave with wavelength `(lambda)/(2)` by the string still oscillating is its fundamental mode, tension must be changed by the multiple.
01:19View Solution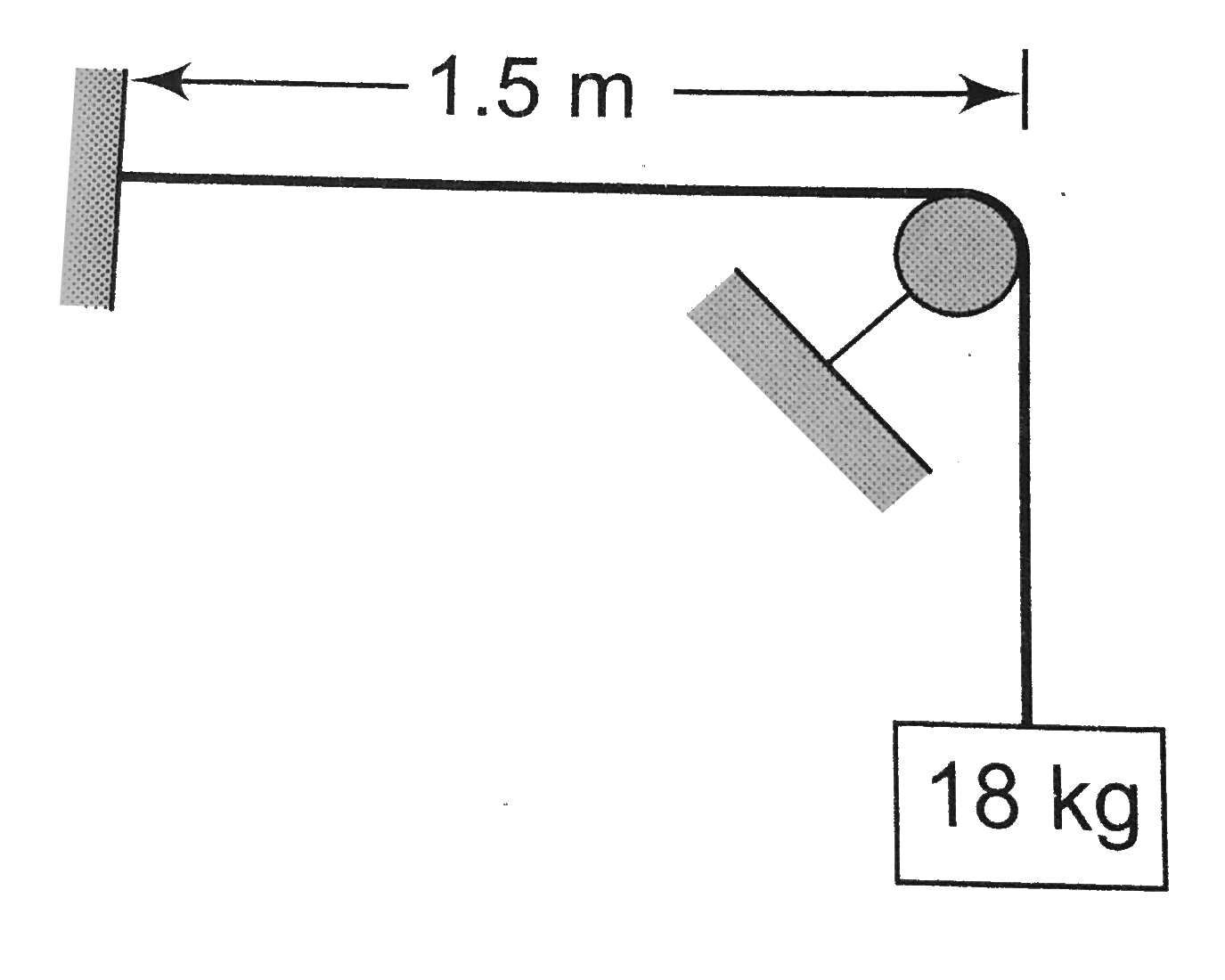
The length of the wire shown in Fig. Between the pulley and fixed support is `1.5m` and mass is `12.0g` the frequency of vibration with which the wire vibrate two loops leaving the middle point of the wire between the pulleys at rest is01:58View SolutionTwo wires are kept tight between the same pair of supports. The tensions in the wires are in the ratio 2 : 1, the radii are in the ratio 3 : 1 and the densities are in the ratio 1 : 2. Find the ratio of their fundamental frequencies.
03:57View Solutionthe fundamental frequency of a sonometer wire of length is `f_(0)`.A bridge is now introduced at a distance of `Deltal`from the centre of the wire `(Deltal lt lt l )`. The number of beats heard if their fundamental mode are
05:20View SolutionA string is fixed at both ends. The tension in the string and density of the string are accurately known but the length and the radius of cross section of the string are known with some errorl If maximum errors made in the measurements of length and radius are `1%` and `0.5%` respectively them what is the maximum possible percentage error in the calculation of fundamental frequencyof the that string ?
02:34View SolutionTwo vibrating string of same length, same cross section area and stretched to same tension is made of materials with densities `rho` and `2rho`. Each string is fixed at both ends If `v_0` represents the fundamental mode of vibration of the one made with density `rho` and `v_2` for another Then `v_1//v_2` is:
01:29View SolutionWhat is the percentage change in the tension necessary in a somometer of fixed length to produce a note one octave lower (half of original frequency) than before?
01:46View SolutionA string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Minimum distance between the two points having amplitude 2 mm is:
05:18View SolutionA chord attached about an end to a vibrating fork divides it into 6 loops when its tension is 36 N. The tension at which it will vibrate 4 loops is:
02:28View SolutionTwo parts of sonometer wire, divided by a movable knife edge differ in length by 2 cm and produce 1 beat/s when sounded together. Assume fundamental frequencies. If the total length of the wire is 100 cm. The frequencies. If the total length of the wire is 100 cm. The frequencies of the two parts of the wire are
02:21View Solution
Vibration Of String questions and complete solutions for chapter WAVES AND ACOUSTICS of A2Z PHYSICS (HINGLISH) of Class 11
