Complete Solutions to Superposition And Interference of chapter WAVES AND ACOUSTICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WAVES AND ACOUSTICS |
| A2Z | Superposition And Interference |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
Two sources of sound `A` and `B` produces the wave of `350 Hz`. They vibrate in the same phase. The particle `P` is vibrating under the influence of these two waves, if the amplitudes at the point P produced by the two waves is `0.3mm` and `0.4mm` then the resultant amplitude of the point `P` will be when `AP-BP=25cm` and the velocity of sound is `350m//sec`.
View SolutionTwo waves are propagating to the point P along a straight line produced by two sources A and B of simple harmonic and of equal frequency. The amplitude of every wave at P is `a` and the phase of A is ahead by `pi//3` than that of B and the distance AP is greater than BP by `50 cm`. Then the resultant amplitude at the point P will be if the wavelength is `1` meter
View SolutionThe minimum intensity of sound is zero at a point due to two sources of nearly equal frequencies when
View SolutionOut of given four waves (1),(2),(3) and (4)
`y=asin(kx+omegat)` ..(1)
`y=asin(omegat-kx)` ..(2)
`y=acos(kx+omegat)` ..(3)
`y=acos(omegat-kx)` ..(4)
emitted by four different source `S_1`,`S_2`,`S_3` and `S_4` respectively, interference phenomena would be observed in space under appropriate conditions when
View SolutionEquation of motion in the same direction is given by `y_1=Asin(omegat-kx)`, `y_2=Asin(omegat-kx-theta)`. The amplitude of the medium particle will be
View SolutionThe amplitude of a wave represented by displacement equation `y=(1)/(sqrta)sinomega+-(1)/(sqrtb)cosomegat` will be
View SolutionTwo waves having equations
`x_1=asin(omegat+phi_1)`, ` x_2=asin(omegat+phi_2)`
If in the resultant wave the frequency and amplitude remain equal to those of superimposing waves. Then phase difference between them is
View SolutionA wave travels on a light string. The equation of the wave is `Y = A sin (kx - omegat + theta))`. It is reflected from a heavy string tied to an end of the light string at `x = 0`. If `64%` of the incident energy is reflected the equation of the reflected wave is
View SolutionIn a large room, a person receives direct sound waves from a source 120 meters away from him. He also receives waves from the same source which reach him, being reflected from the 25 meter high ceiling at a point halfway between them. The two waves interfere constuctively for wavelength of
View SolutionTwo speakers connected to the same source of fixed frequency are placed 2.0m apart in a box. A sensitive microphone placed at a distance of 4.0 m from their midpoint along the perpendicular bisector shows maximum response. The box is slowly rotated until the speakers are in line with the microphone. The distance between the midpoint of the speakers and the microphone remains unchanged. Exactly five maximum responses are observed in the microphone in doing this. the wavelength of the sound wave is
View Solution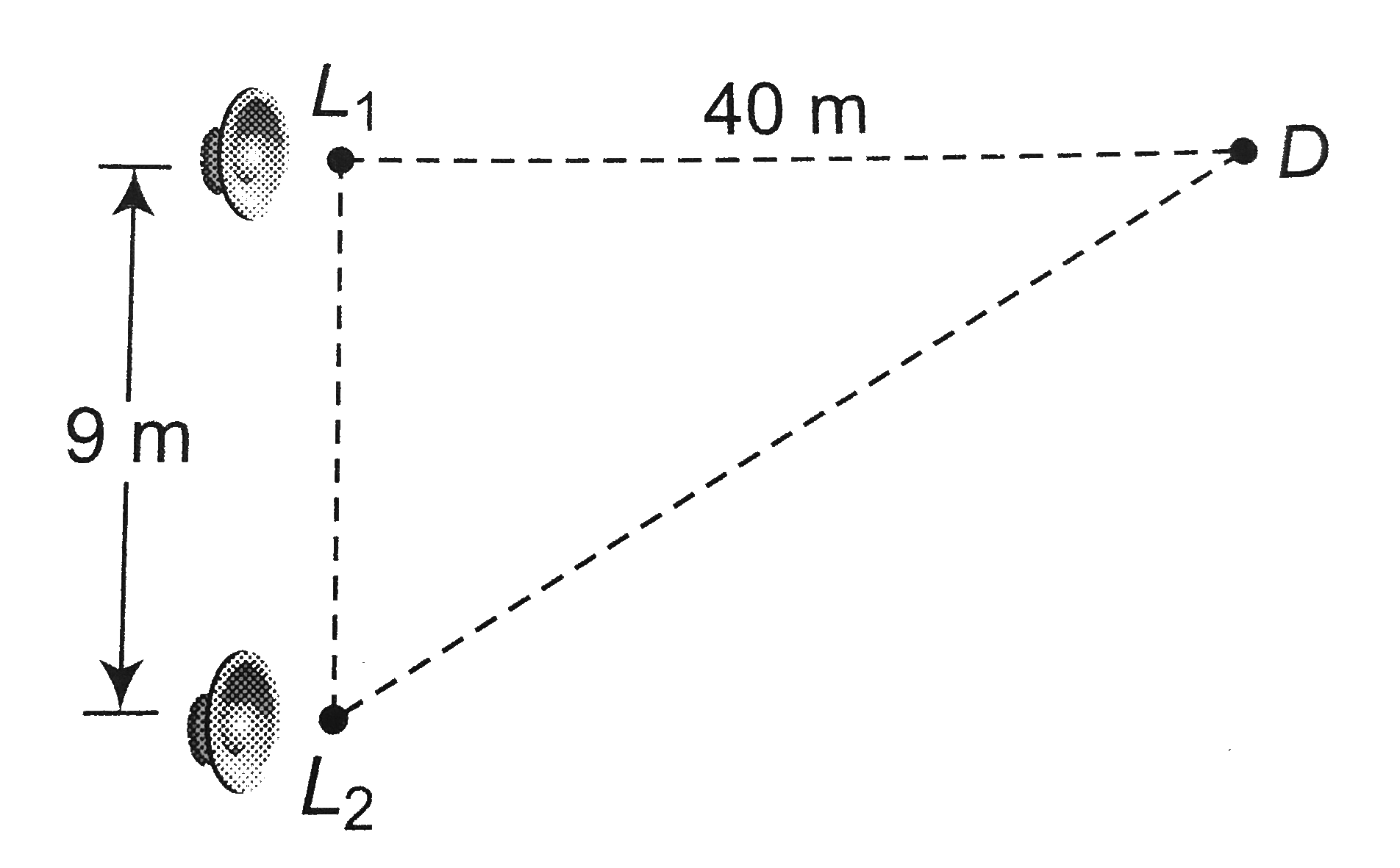
Two loudspeakers `L_1` and `L_2` driven by a common oscillator and amplifier, are arranged as shown. The frequency of the oscillator is gradually increased from zero and the detector at D records a series of maxima and minima. If the speed of sound is `330ms^-1` then the frequency at which the first maximum is observed is
View SolutionTwo pulses travel in mutually opposite directions in a string with a speed of `2.5 cm//s` as shown in the figure. Initially the pulses are `10 cm` apart. What will be the state of the string after two seconds?
View Solution
Two pulses are travelling along a string in opposite directions towards each other as shown in the figure. If the wave velocity is `2cm//s` and the pulses are 6 cm apart, then after `1.5 sec`, the energy stored in the string will be (Assume shapes of pulses to be similar)
View SolutionThere are `10` sound sources each producing intensity I at a point independently. They are incoherent. Average intensity of sound at that point will be:
View SolutionTwo coherent sources of different intensities send waves which interfere. The ratio of maximum intensity to the minimum intensity is 25. The intensities of the sources are in the ratio
View SolutionA string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cm and 16 cm respectively. The minimum possible length of the string (in cm) is:
View Solution
When a wave pulse travelling in a string is reflected from rigid wall to which string is tied as shown in figure. For this situation two statements are given below.
(1) The reflected pulse will be in same orientation of incident pulse due to a phase change of `pi` radians
(2) During reflection the wall exert a force on string in upward direction
View Solution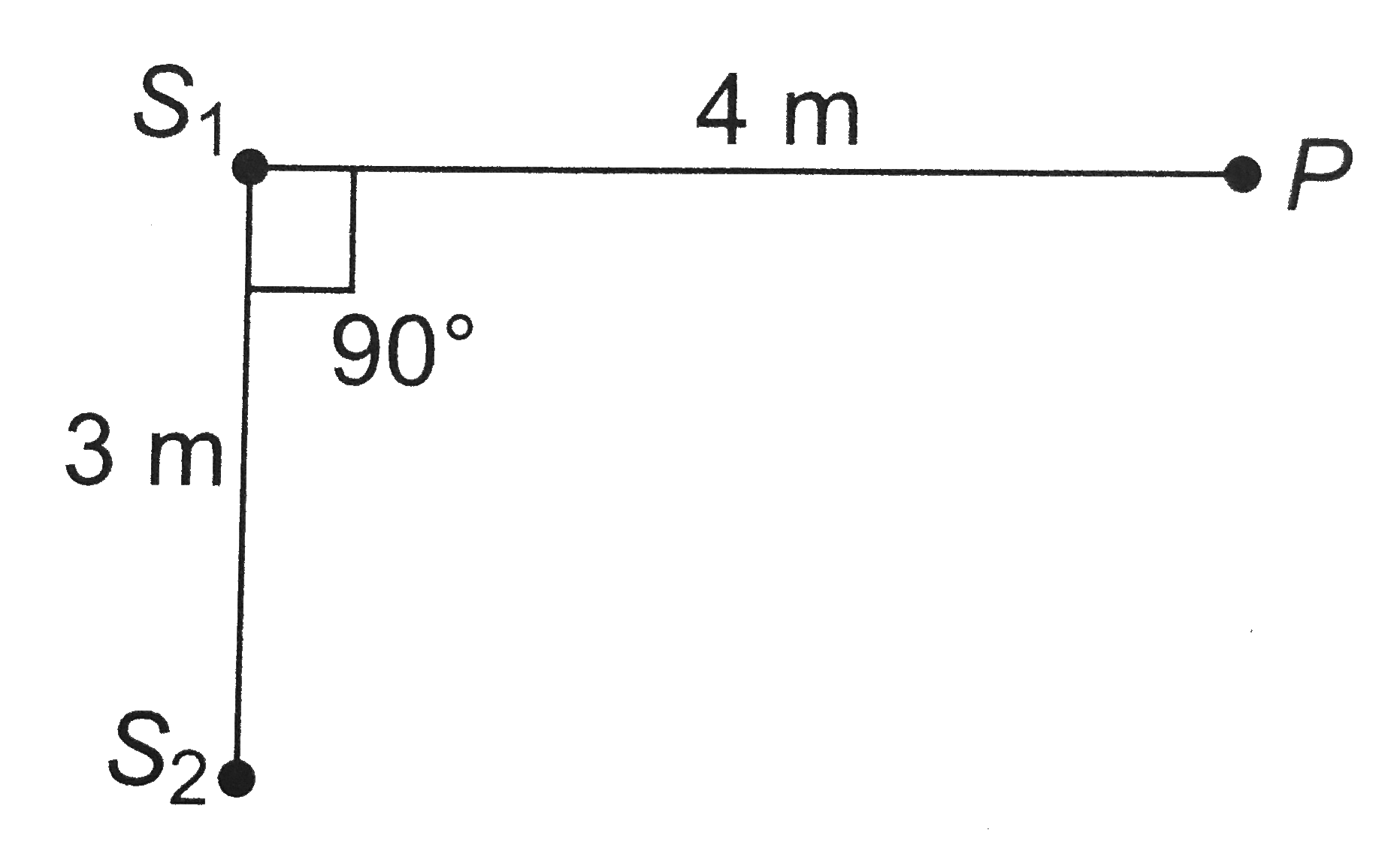
`S_(1)` and `S_(2)` are two coherent sources of sound of frequency `110Hz` each they have no initial phase difference. The intensity at a point P due to `S_(1)` is `I_0` and due to `S_2` is `4I_0`. If the velocity of sound is `330m//s` then the resultant intensity at P is
View Solution
In the figure the intensity of waves arriving at D from two coherent sources `S_1` and `S_2` is `I_0` The wavelength of the wave is `lamda=4m`. Resultant intensity at D will be:
View SolutionTwo interfering waves have intensities in the ratio `9:1`. Then the ratio of maximum to minimum intensity is:
View SolutionThe difference of loudness in decibels `(dB)` between maximum and minimum intensities of two coherent sound sources as they interfere in space is `20log3`. Find the ratio of intensities of two coherent sound sources:
View Solution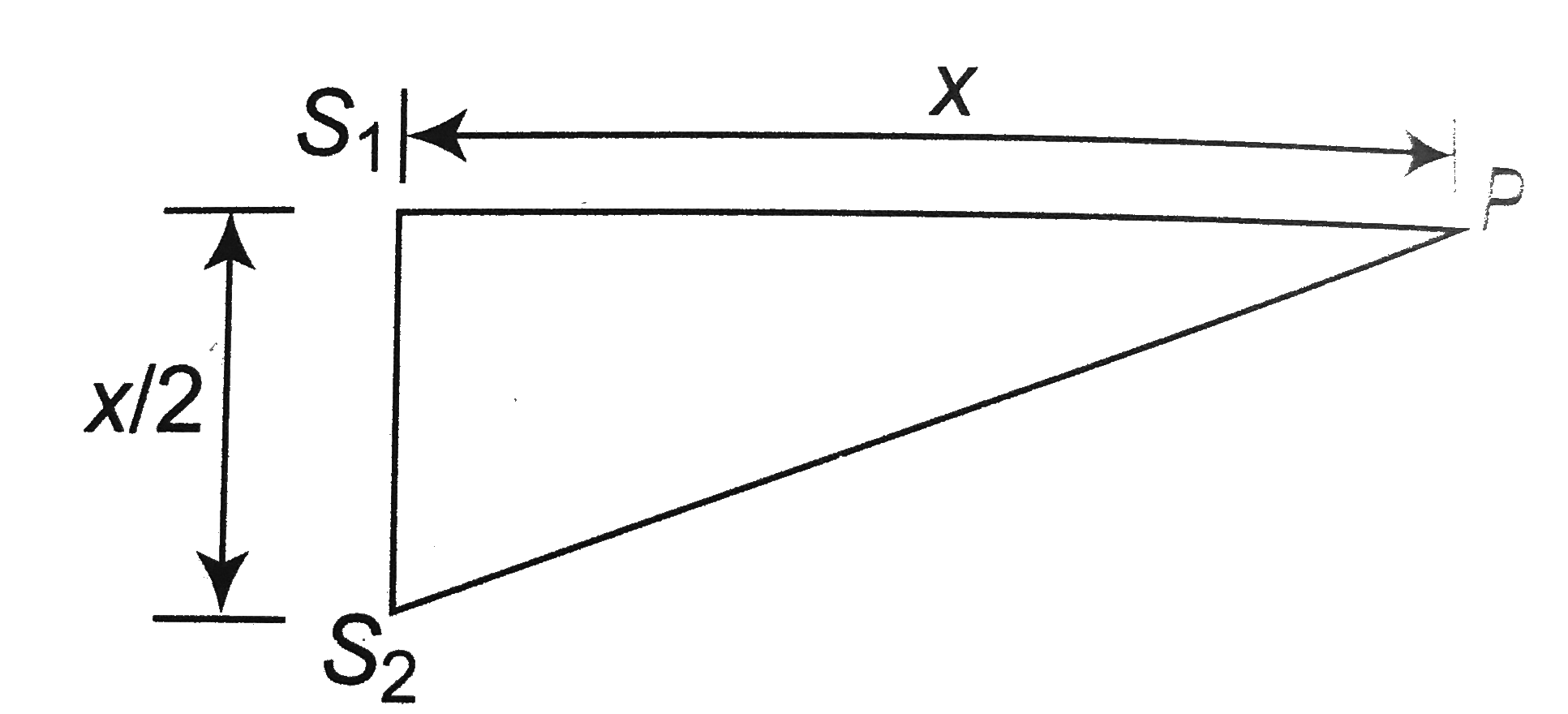
The wavelength of the waves arriving at P from two coherent sources `S_1` and `S_2` is 4m, while intensity of each wave is `I_0`. The resultant intensity at `P` is `2I_0`. Find the minimum value of `S_2P`
View Solution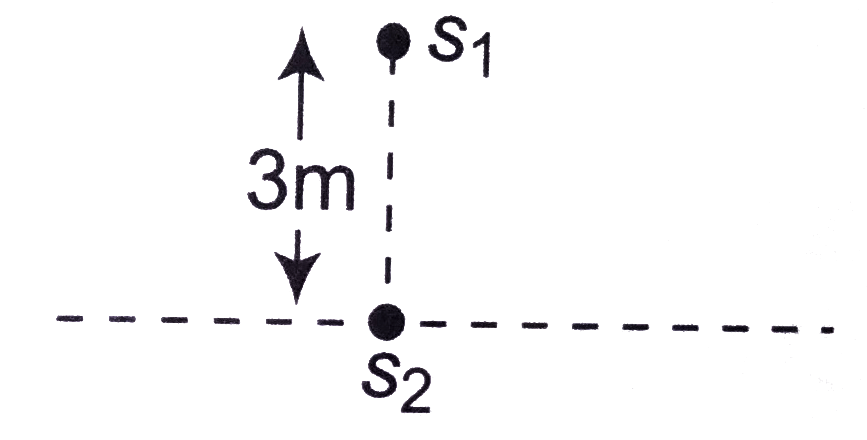
`S_1` and `S_2` are two coherent sources of sound having no initial phase difference. The velocity of sound is `330m//s`. No minima will be formed on the line passing through `S_2` and perpendicular to the line joining `S_1` and `S_2`. If the frequency of both the sources is:
View Solution
Superposition And Interference questions and complete solutions for chapter WAVES AND ACOUSTICS of A2Z PHYSICS (HINGLISH) of Class 11