Complete Solutions to Level-3 of chapter DESCRIPTION OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | DESCRIPTION OF MOTION |
| ANURAG MISHRA | Level-3 |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
A particle 'A' starts moving frorri point A with constant velocity 4 m/s along x-axis. Another particle 'B' initially at rest starts moving along x-axis after (8/3), sec after the start of A, with acceleration varying `a=4=(3-t) m//s^(2)`
Particle B will stop again at the position x equal to :
View SolutionA particle 'A' starts moving frorri point A with constant velocity 4 m/s along x-axis. Another particle 'B' initially at rest starts moving along x-axis after (8/3), sec after the start of A, with acceleration varying `a=4=(3-t) m//s^(2)`
The two particles will meet twice in the due course of their motion. The time interval between these two successive meets will be :
View SolutionA particle 'A' starts moving frorri point A with constant velocity 4 m/s along x-axis. Another particle 'B' initially at rest starts moving along x-axis after (8/3), sec after the start of A, with acceleration varying `a=4=(3-t) m//s^(2)`
Position where the two particles will meet for the second time is given by :
View SolutionA particle 'A' starts moving frorri point A with constant velocity 4 m/s along x-axis. Another particle 'B' initially at rest starts moving along x-axis after (8/3), sec after the start of A, with acceleration varying `a=4=(3-t) m//s^(2)`
Total distance traveled by the particle B when it meets the particle A for the second time is :
View SolutionA particle 'A' starts moving frorri point A with constant velocity 4 m/s along x-axis. Another particle 'B' initially at rest starts moving along x-axis after (8/3), sec after the start of A, with acceleration varying `a=4=(3-t) m//s^(2)`
Magnitude of the relative velocity of the two particles when they meet for the first time is :
View SolutionA particle 'A' starts moving frorri point A with constant velocity 4 m/s along x-axis. Another particle 'B' initially at rest starts moving along x-axis after (8/3), sec after the start of A, with acceleration varying `a=4=(3-t) m//s^(2)`
Magnitude of the relative velocity of the two particles when they meet for the second time is :
View SolutionA particle 'A' starts moving frorri point A with constant velocity 4 m/s along x-axis. Another particle 'B' initially at rest starts moving along x-axis after (8/3), sec after the start of A, with acceleration varying `a=4=(3-t) m//s^(2)`
Variation of velocity uf the particle B with time is best represented by :
View SolutionA swimmer wishes to .cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle` theta` with the perpendicular as shown ip. the. figure.
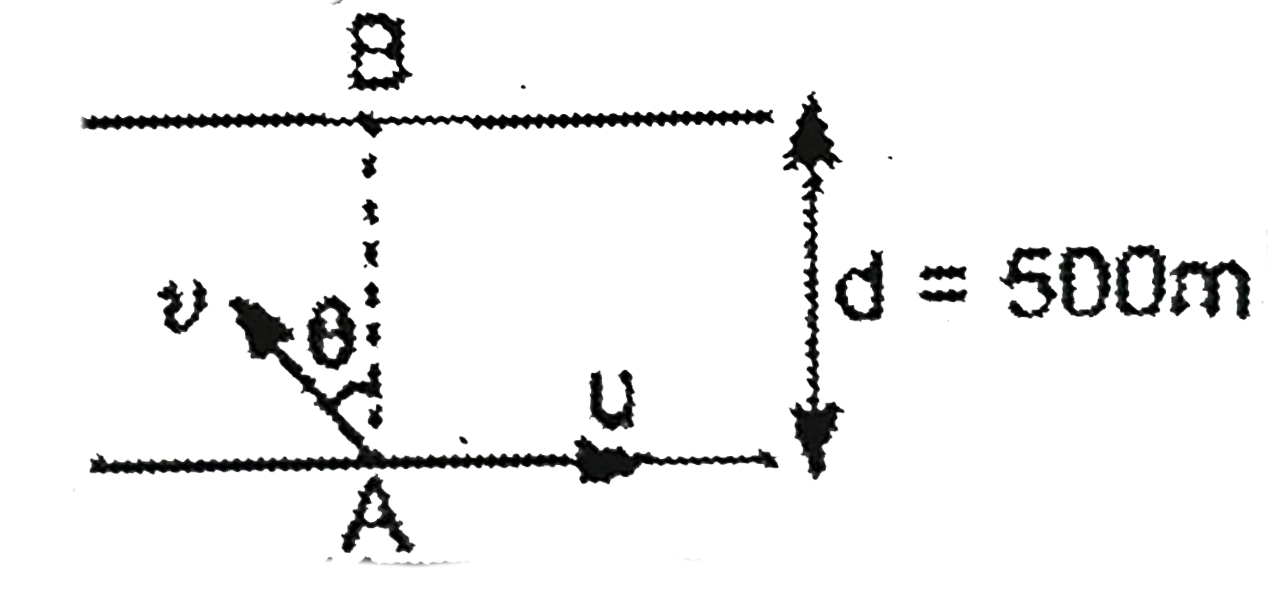
To cross the river in minimum time, the value of `theta` should be:
View SolutionA swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle` theta` with the perpendicular as shown in the figure.

To cross the river in minimum time, the value of `theta` should be.
View SolutionA swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle ` theta` with the perpendicular as shown in the figure.
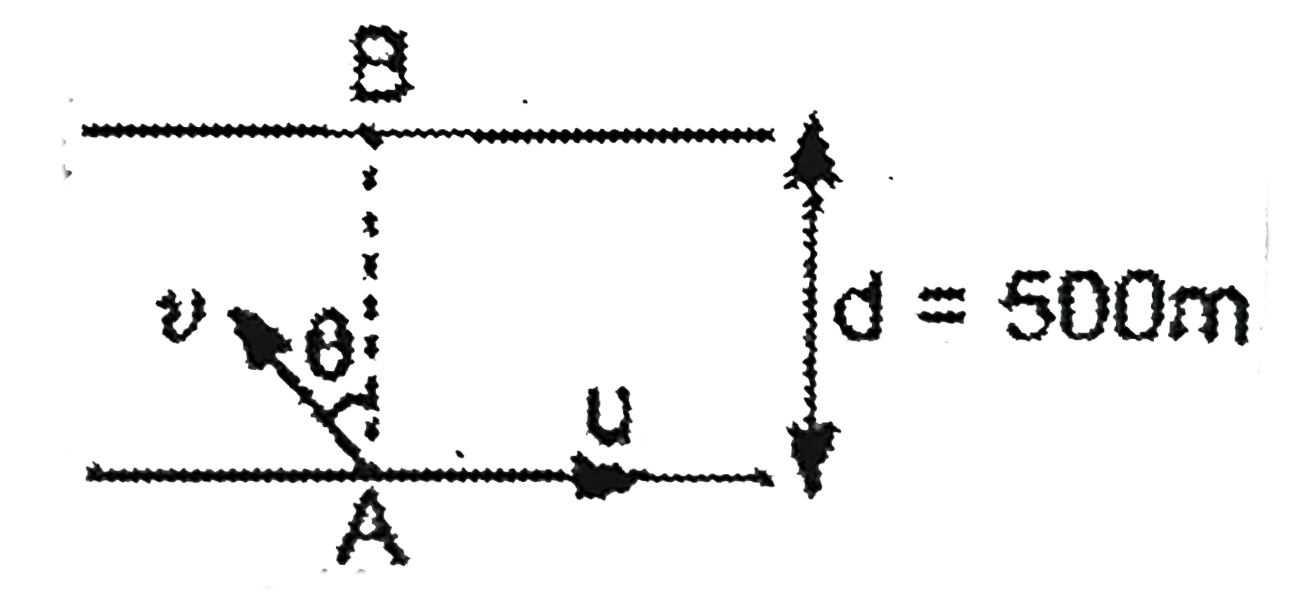
For u = 3 km/hr and v = 5 km/hr, the time taken to cross the river in minimum time will be :
View SolutionA swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle` theta` with the perpendicular as shown in the figure.

To cross the river in minimum time, the value of `theta` should be.
View SolutionA swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle` theta` with the perpendicular as shown in the figure.

To cross the river in minimum time, the value of `theta` should be.
View SolutionA swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle` theta` with the perpendicular as shown in the figure.

To cross the river in minimum time, the value of `theta` should be.
View SolutionA swimmer wishes to cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle` theta` with the perpendicular as shown in the figure.

To cross the river in minimum time, the value of `theta` should be.
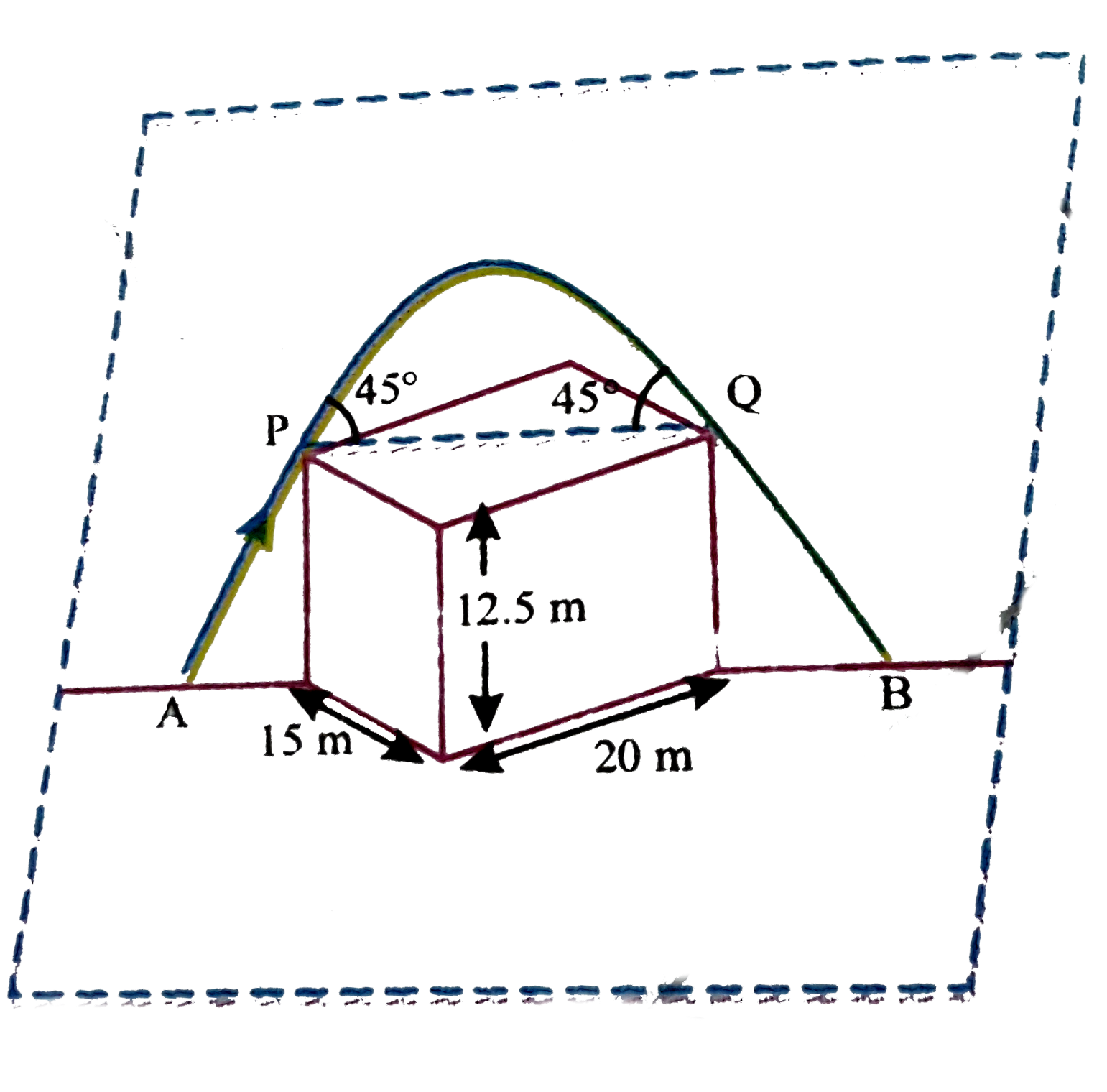
View SolutionA particle is fired from `A` in the diagonal plane of a building of dimension `20m`(length) `xx` `15m` (breadth) `xx` `12.5 m`(height), just clears the roof diagonally & falls on the other side of the building at `B`.It is observed that the particle is travelling at an angle `45^(@)` with the horizontal when it clears the edges `P` and `Q` of the diagonal. Take `g=10m//s^(2)`.
The speed of the particle at point `P` will be:
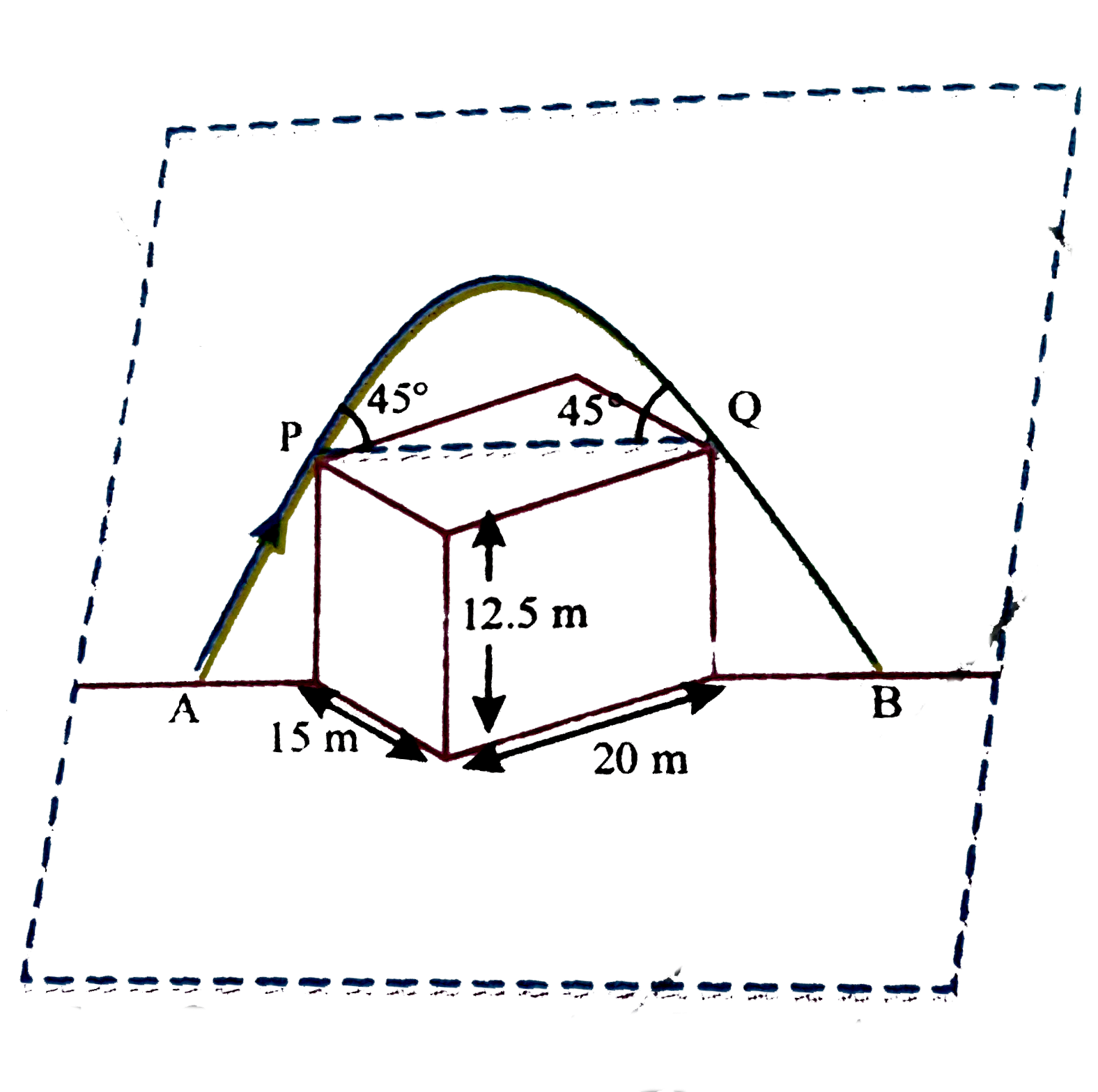
View SolutionA particle is fired from 'A' in the diagonal plane of building of dimension 20 m (length)x 1.5 m (breadth) x 12.5 m (height) , just clears the roof diagonally & falls on the other side of the building at B. it is observed that the particle is travelling at an angle `45^(@)` with the horizontal whtn it clears tha edges P and Q of the diagonal Take g=`10 m//s^(2)`

The angle pf projection at A will be :
View SolutionA particle is fired from `A` in the diagonal plane of a building of dimension `20m`(length) `xx` `15m` (breadth) `xx` `12.5 m`(height), just clears the roof diagonally & falls on the other side of the building at `B`.It is observed that the particle is travelling at an angle `45^(@)` with the horizontal when it clears the edges `P` and `Q` of the diagonal. Take `g=10m//s^(2)`.
The speed of projection of the particle at `A` will be:
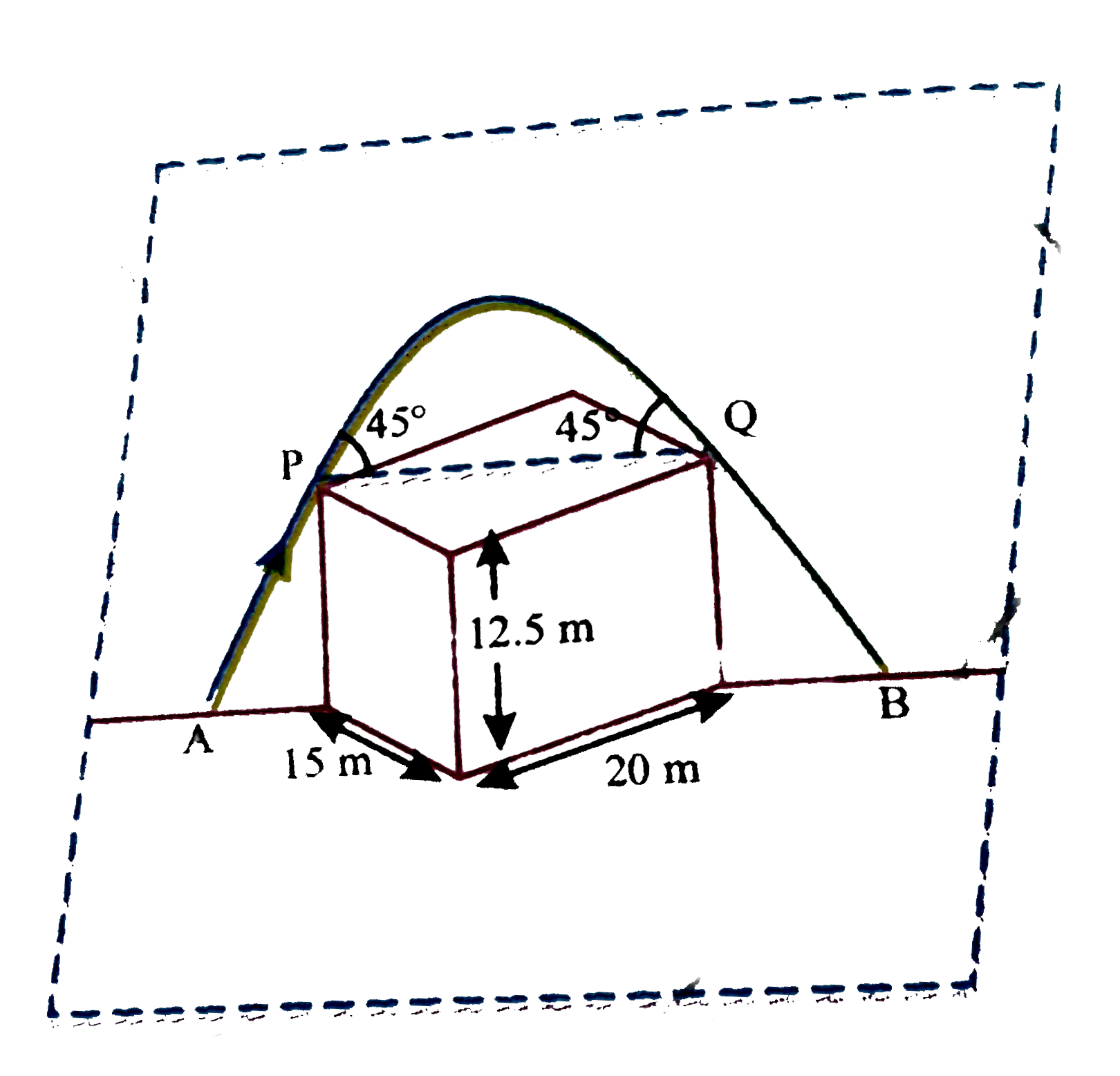
View SolutionA particle is fired from `A` in the diagonal plane of a building of dimension `20m`(length) `xx` `15m` (breadth) `xx` `12.5 m`(height), just clears the roof diagonally & falls on the other side of the building at `B`.It is observed that the particle is travelling at an angle `45^(@)` with the horizontal when it clears the edges `P` and `Q` of the diagonal. Take `g=10m//s^(2)`.
The speed of the particle at point `P` will be:

View SolutionA particle is fired from `A` in the diagonal plane of a building of dimension `20m`(length) `xx` `15m` (breadth) `xx` `12.5 m`(height), just clears the roof diagonally & falls on the other side of the building at `B`.It is observed that the particle is travelling at an angle `45^(@)` with the horizontal when it clears the edges `P` and `Q` of the diagonal. Take `g=10m//s^(2)`.
The range that is `AB` will be:
View SolutionA dart gun is fired towards a Squirrel hanging from a tree. Dart gun was initially directed towards Squirrel. P is maximum height attained by dart in its flight. Three different events can occur. (Assume Squirrel to be a particle and there is no air resistance) .
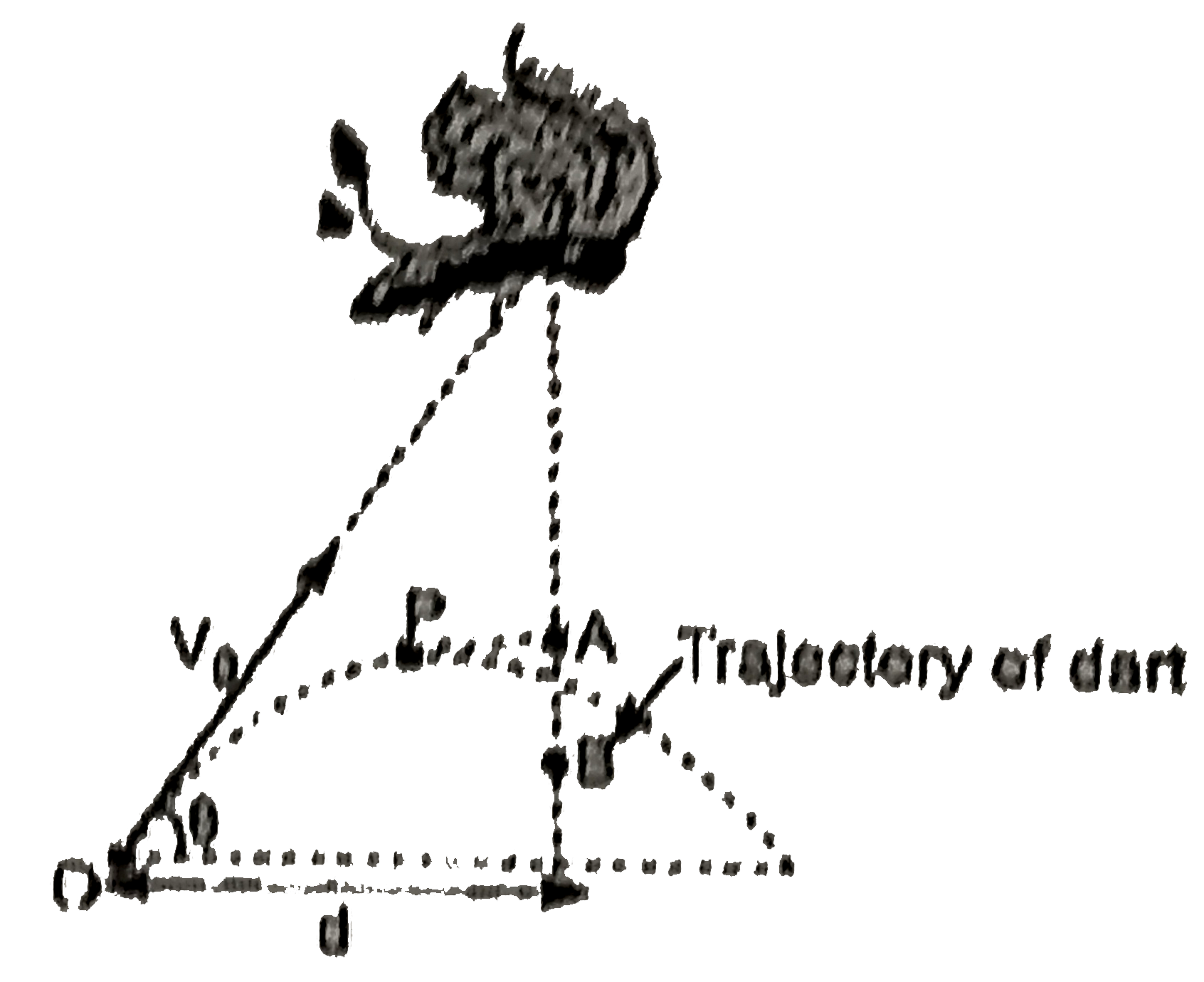

View SolutionColumn-1 shows certain situations with certain conditions and column-2 shows the parameters in which situations of column-1 match. Which can be possible combination.

View SolutionColumn-1 shows certain situations with certain conditions and column-2 shows the parameters in which situations of column-1 match. Which can be possible combination.

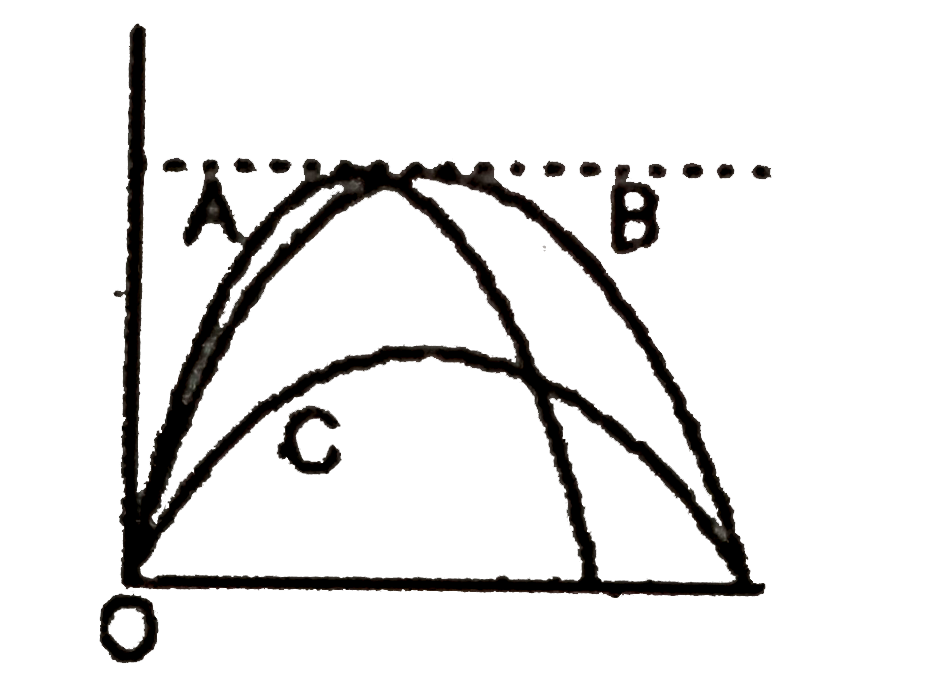
View SolutionTrajectories are shown in figure for three kicked footballs. Initial vertical and horizontal velocity components are `u_(y)` and `u_(x)` respectively. Ignoring air resistance, choose the correct statement from column-2 for the value of variable in column-1.

View SolutionShown a vector `vec(a)` angle `theta` as shown in the figure column-2. Show its unit vector representation .


View SolutionConsider an object at point P along each trajectory shown in column-1 in the direction of arrow shown. Column-2 gives algebraic sign of `v_(x), v_(y), a_(x)` and `a_(y)` .
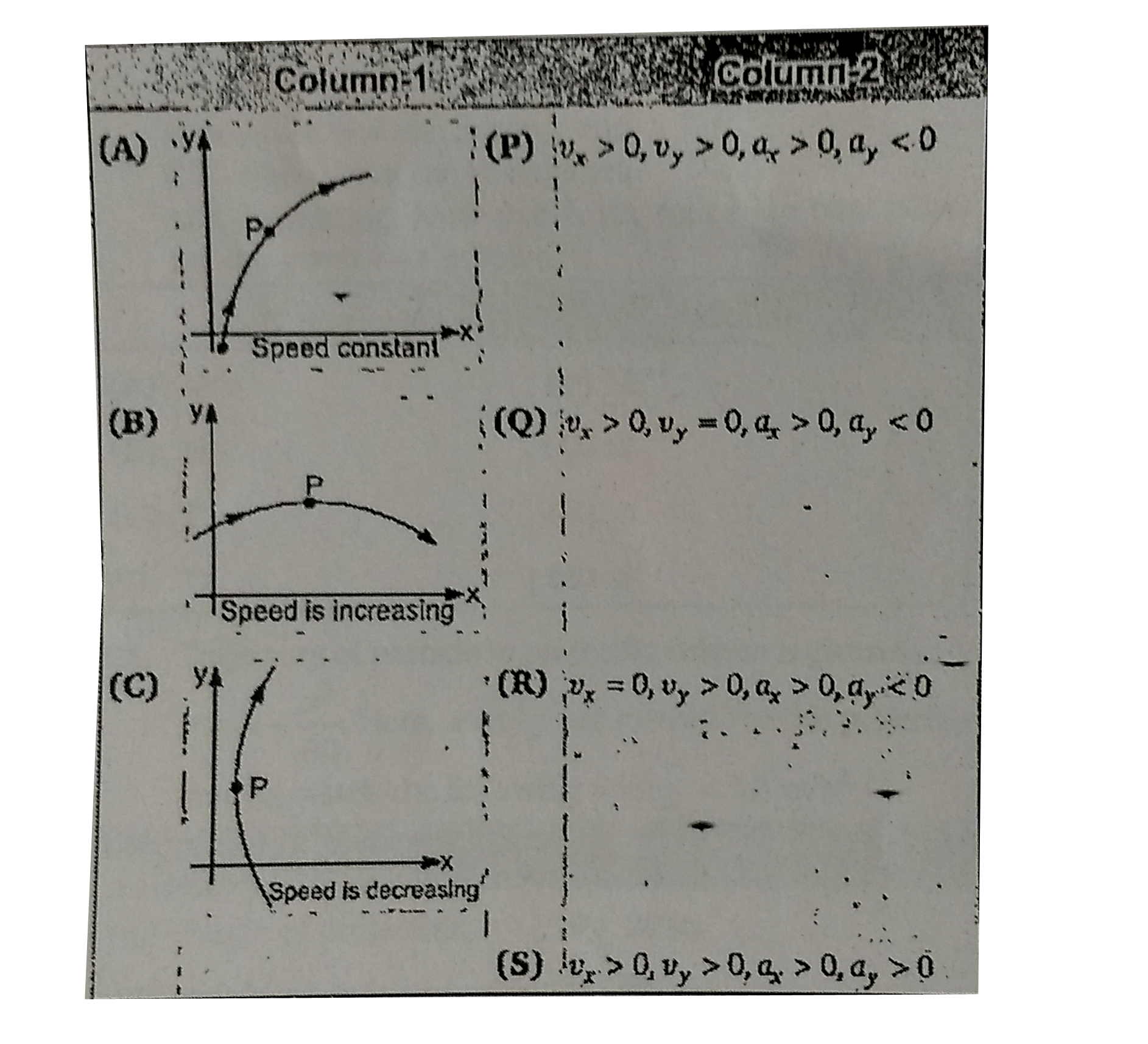
View SolutionA particle is moving along a straight line. Its v-t graph is as shown in figure. Point l, 2 and 3 marked on graph are three different instants. Column-1 has fill in the blanks, which are to be filled by the entries in column-2.


View SolutionFigure shows a cube of edge lenth a
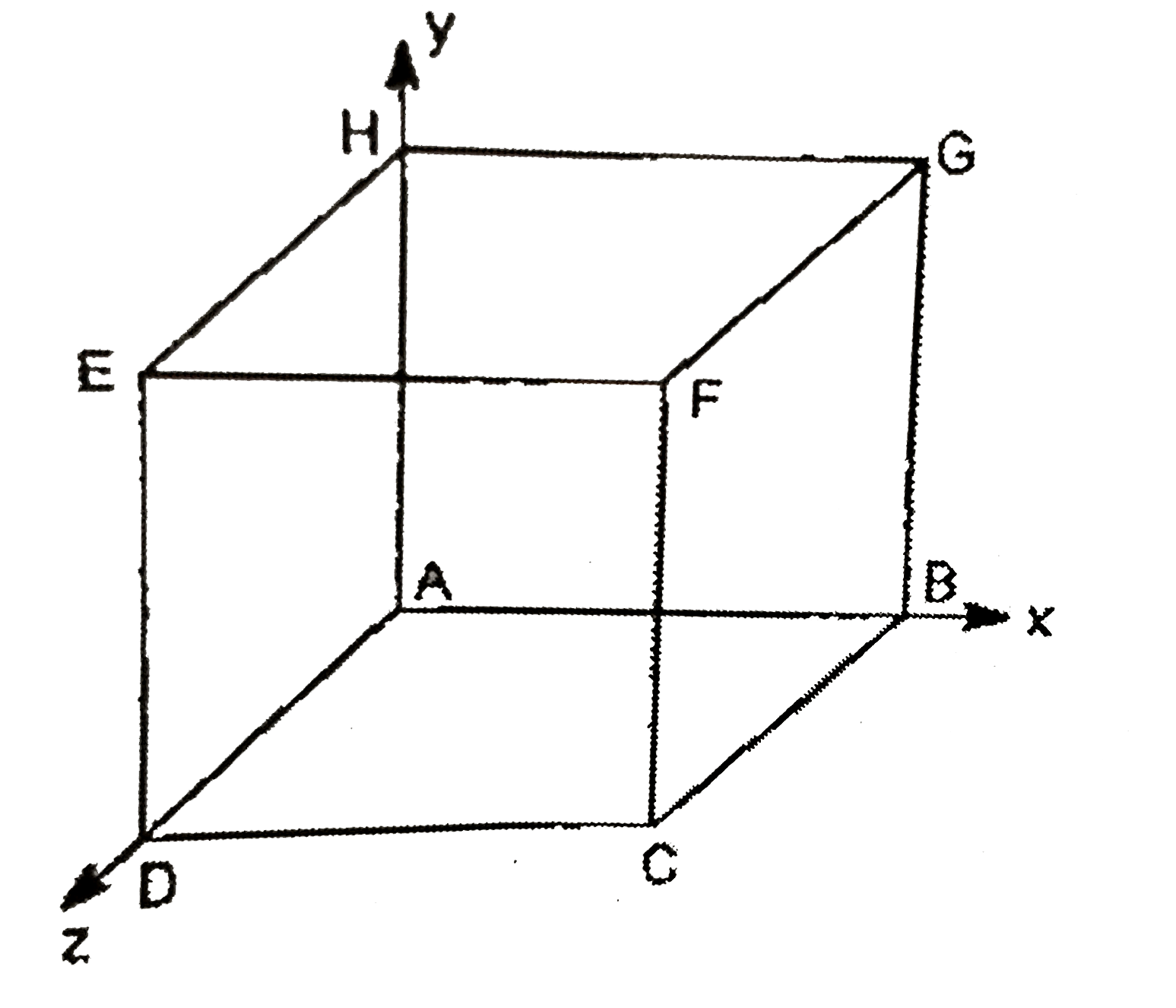

View SolutionMatch the following :



View SolutionFor the velocity -time graph shown in figure, in a time interval from `t=0` to `t=6 s`, match the following:
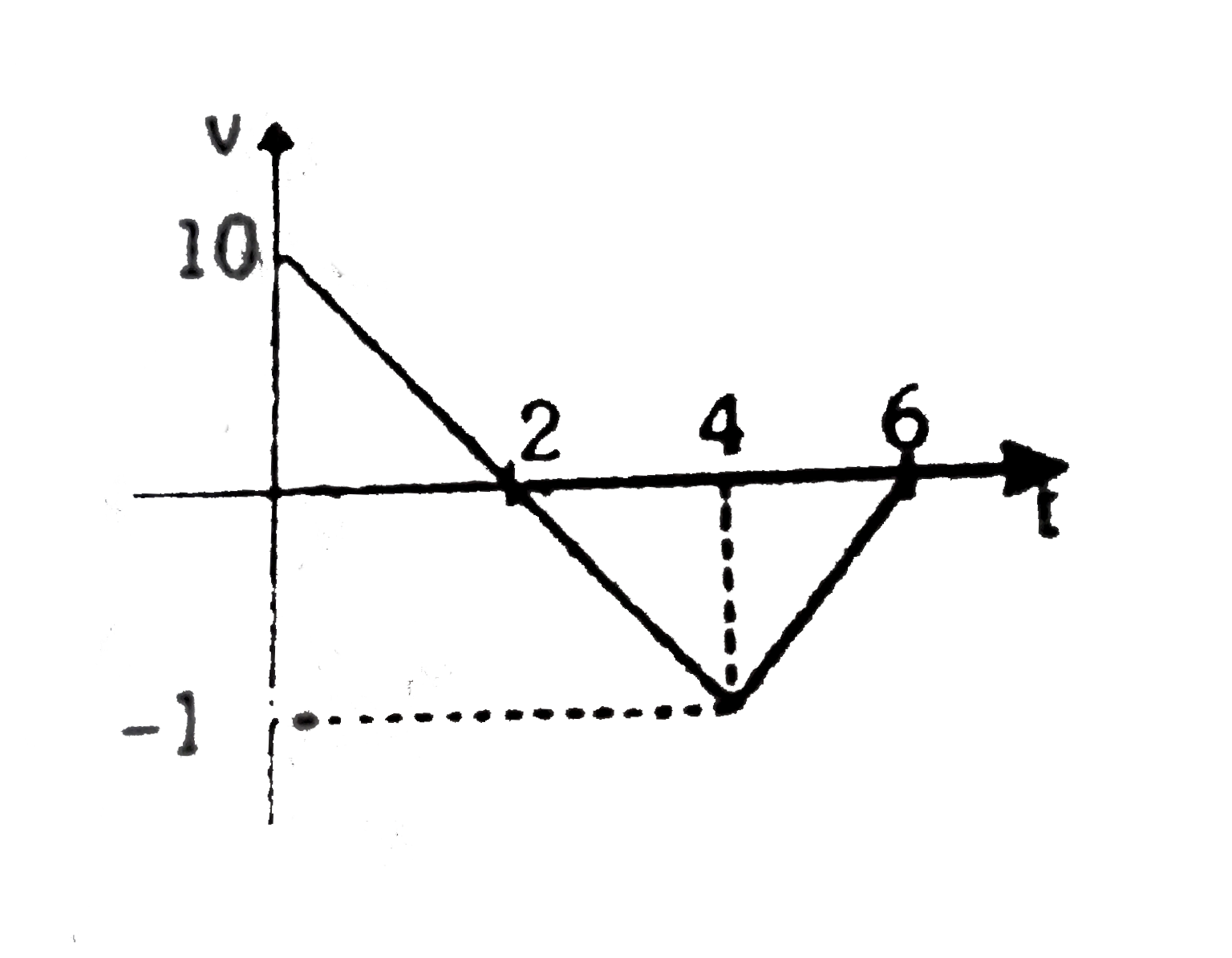
`{:(,"Column I",,,"Column II"),((A),"Change in velocity",,(p),-5//3 SI "unit"),((B),"Average acceleration",,(q),-20 SI "unit"),((C),"Total displacement",,(r),-10 SI "unit"),((D),"Acceleration ay t=3s",,(s),-5 SI "unit"):}`
View SolutionAssertion : A body can have acceleration even if its velocity is zero at a given instant of time.
Reason : A body is momentarily at rest when it reverses its direction of motion.
View SolutionAssertion : A body having uniform speed is circular path has a constant acceleration .
Reason : Direction of acceleration is always away from the centre.
View SolutionAssertion: Two bodies of masses `M` and `m(M gt m)` are allowed to fall from the same height if the air resistance for each be the same then both the bodies will reach the earth simultaneously.
Reason: For same air resistance, acceleration of both the bodies will be same.
View SolutionStatement I: A body can have acceleration even if its velocity is zero at a given instant .
Statement II: A body is momentarily at rest when it reverses its direction of velocity.
View SolutionSTATEMENT-1: A particle in motion may not have variable speed but constant velocity.
STATEMENT-2: A particle having non-zero acceleration may move with constant speed.
View Solution
Level-3 questions and complete solutions for chapter DESCRIPTION OF MOTION of SHREE BALAJI PHYSICS (HINGLISH) of Class 11