Complete Solutions to Example of chapter DESCRIPTION OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | DESCRIPTION OF MOTION |
| ANURAG MISHRA | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
A bird ,moves with velociry 20 m/ s in a direction making an, :angle of `60^(@)` with the eastern line and `60^(@)` with verticalj lupward~present the velocity vector in rectan!(Ular form.
View SolutionTwo vectors, both equal in magnitude, hav. e their resultant!! !equal in magnitude of the either vector. Find the angle between the vectors.
View SolutionThe sum of the magnitudes of two forces acting at a point is 18 and the magnitude of their resultant is 12. If the resultant is at `90^(@)` with the force of smaller magnitude, What are the magnitudes of forces?
View Solution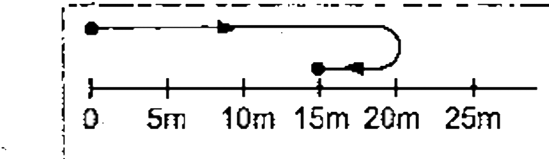
A student starts from his physics classroom considered to bel !origin, walks 20 m down the corridor, then stops, turns ,around and walks 5.0 m back towards the classroom. He stops 15.0 mfrom the door. Tota1time of motion is 25.0 sec. What is his average speed and average velociry?
View SolutionConsider three vectors `vecA,vecB and vecC` as shown in fig. perform graphically the following vector additions and subtractions (a) `vecA+vecB`
(b). `vecA+vecB+vecC`
(c). `vecA-vecB`
(d). `vecA+vecB-vecC`

View SolutionVector `vecA=3hati+5hatj-2hatk` and vector `vecB=-3hatj+6hatk` find a, vector `vecC` such that `2vecA+7vecB+4vecC=0`
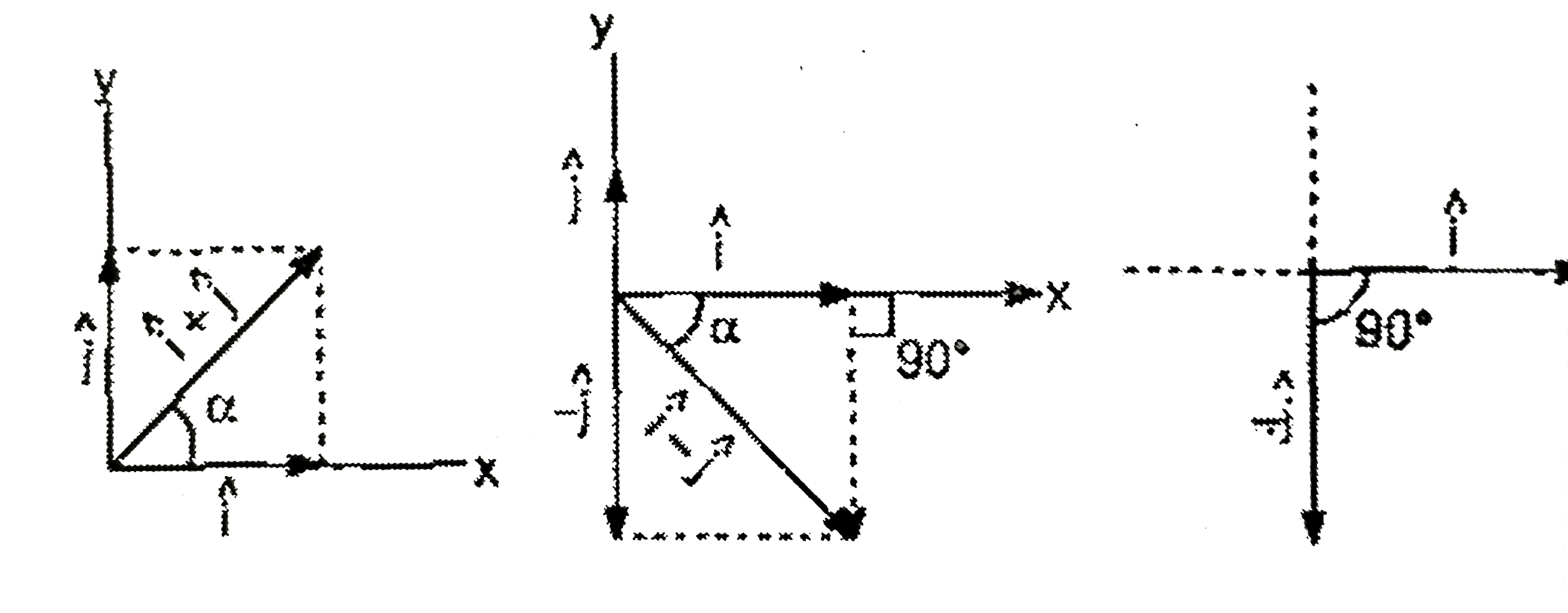
View SolutionTwo unit vectors `hati` and `hatj` are directed along x-axis and y-axis respectively. What is the magnitude and direction of the vectors `hati+hatj and hati-hatj`?
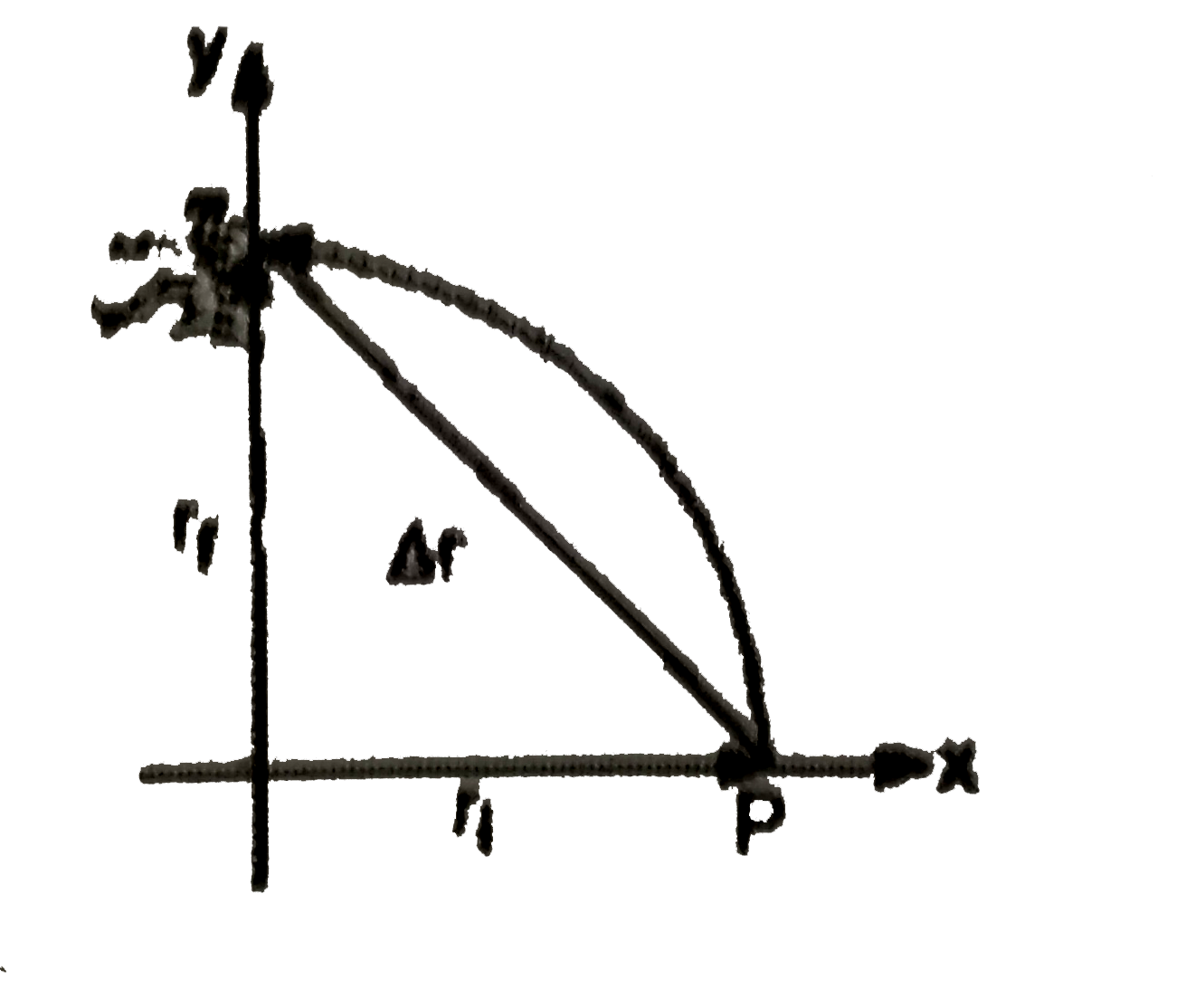
View SolutionA girl is jogging along a circular path of radius. 25. 0 m. In 1 110.0 second she jogs a. quarter ofa circle starting from point1 P. (a) Compute her displacement and average velocity, and (b) Compute the magnirude of the runner's average velocity and her average speed.
View SolutionFind he component of `veca=2hati+3hatj` along the direction of vectors `(hati+hatj)`
View SolutionIf `vecA=3hati+4hatj` and `vecB=7hati+24hatj`, find a vector having the same magnitude as `vecB` and parallel and same direction as `vecA`.
View SolutionUnder a fore `(10hati-3hatj+6hatk)` newton a bod of mass 5 kg moves from position `(6hati+5hatj-3hatk)` m to position `(10hati-2hatj+7hatk)`m. deduce the work done.
View SolutionA particle moves in the x-y plane under the action of a force `vecF` such that the value of its linear momentum `vecP` at any time t is `P_(x)=2` cost and `p_(y)=2sint`. What is the angle `theta` between `vecF` and P at a given time t?
View SolutionThe velocity of a particle is `3hati+2hatj+3hatk`. Find the vector component of the velocity along the line `hati-hatj+hatk` and its magnitude.
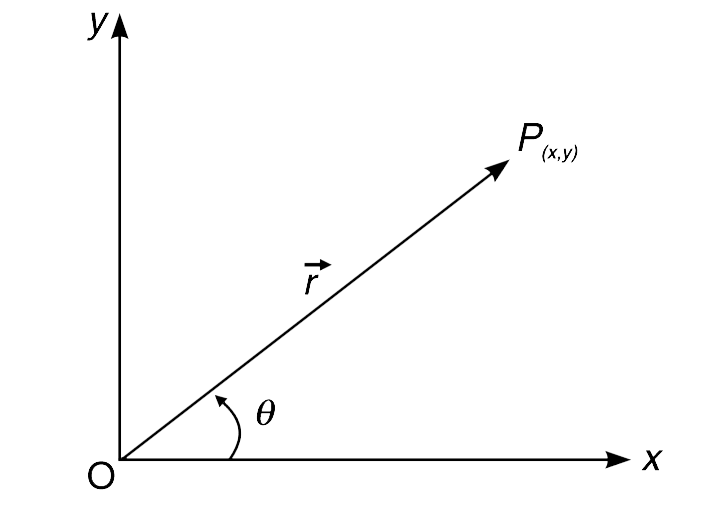
View SolutionA particle has co-ordinates (x, y). Its position vector makes on angle `theta` with positive x direction. In an infinitesimally small interval of time the particle moves such that length of its position vector does not change but angle `theta` increases by `d theta`. Express the change in position vector of the particle in terms of x, y, `d theta` and unit vectors `hati` and `hatj`.
View SolutionIf two non-zero vectors `vecA` and `vecB` obey the relation `vecA+vecB=vecA-vecB`, the angle between them is
(a). `120^(@)`
(b). `90^(@)`
(c). `60^(@)`
(d). `0^(@)`
View Solution`hati` and `hatj` are unit vectors along x-axis and y-axis respectively what is the magnitude and direction of the vector `hati+hatj` and `hati-hatj` ? What are the magnitudes of components of a vector `veca=2hati+3hatj` along the directions of `hati+hatj and hati-hatj`?
View SolutionGiven `veca=hati+2hatj+3hatk,vecb=-hati++2hatj+hatk and vec c=3hati+hatj` find the angle of resultant with x-axis. Also finid a unit vector in the direction of the resultant of these vectors. Also find a unit vecotr `vecr` which is normal to both `veca and vecb` what is the inclination of `vecr and vec c`?
View SolutionIf `veca=2hati+3hatj+6hatk` and `vecb=6hati+3hatj-2hatk`, find the angle, between vectors `veca and vecb`. Also find unit vector perpendicular to both `veca and vecb`
View SolutionA cyclist starting from a point A travels 200m due north to a point B at constant speed of 5 `ms^(-1)`. He rests at B for 30 seconds and then travels 300 m due south to a point G at a constant speed of `10ms^(-1)` find average velcity.
View SolutionA particle is travelling in a straight line, it has a initial velocity of `10ms^(-1)`. When it is subjected to an acceleration of `-2ms^(-2)` for 8 sec. find displacement and distance traversed in 8 sec.
View SolutionA particle moves in a straight line with constant velocity of 5 `ms^(-1)` for 2 sec. it then moves with a constant acceleration of `-2ms^(-2)` for 8 sec. draw velocity-time graph for 10 sec of motion and find
(a). Final velocity
(b). Displacement
(c). Total distance.
View SolutionDifferentiate
(a). `f(x)=(1)/(x^(2))`
(b). `y=root2(x^(2))`
View SolutionFind the points on the curve `y=x^(4)-6x^(2)+4` where the tangent line is horizontal.
View Solutionif `f(x)=xe^(x)` find `f'(x)`
View SolutionDifferentiate the function `f(t)=sqrt(t)(1-t)`
View Solutionif `f(x)=sqrt(xg)(x)` where `g(4)=2` and `g(4)=3,findf(4)`
View SolutionFind an equation of the tangent line to the curve `y=e^(x)//(1+x^(2))` at the point `(1,e//2)`
View Solutiondifferentiate `y=x^(2)sinx`.
View SolutionDifferentiate `y=tanx`
View SolutionFind `F'(x)` if `(F(x)=sqrt(x^(2)+1))`
View SolutionDifferentiate `y=(x^(3)-1)^(100)`
View SolutionFind `f(x)` if `f(x)=(1)/(root3(x^(2)+x+1))`
View Solutionfind the derivative of the function
`g(t)=((t-2)/(2t+1))^(9)`
View SolutionDefferentiate `y=e^(sinx)`
View SolutionLet `s(t)=t^(3)-6t^(2)` be the position function of a particle moving along an s-axis, where s is in meters and t is in sec. find the instantaneous acceleration a(t) and show the graph of acceleration versus time.
View SolutionThe po9sition of aparticle is given by the equation.
`s=f(t)=t^(3)-6t^(2)-9t`
where r is is measure in seconds and s in meters.
(a). Find the velocity at the t
(b). What is thhe velocity after 2s ? After 4 s ?
(c). When is the particle at rest ?
(d). When is the particle moving formward that is, ini the positive direction)?
(e). Find the total distance traveled by the particle during the first five sec.?
View Solutionsketh the region whose area is represented by the definite integral and evaluat the integral using an appropriate formula form geometry.
(a). `int_(1)^(4) 2dx`
(b). `int_(-1)^(2) (x+2)dx`
(c) `int_(0)^(1) sqrt(1-x^(2))dx`
View SolutionEvaluate
(a). `int_(0)^(2)(x-1)dx`
(b). `underset(0)overset(2)(x-1)dx`
View Solution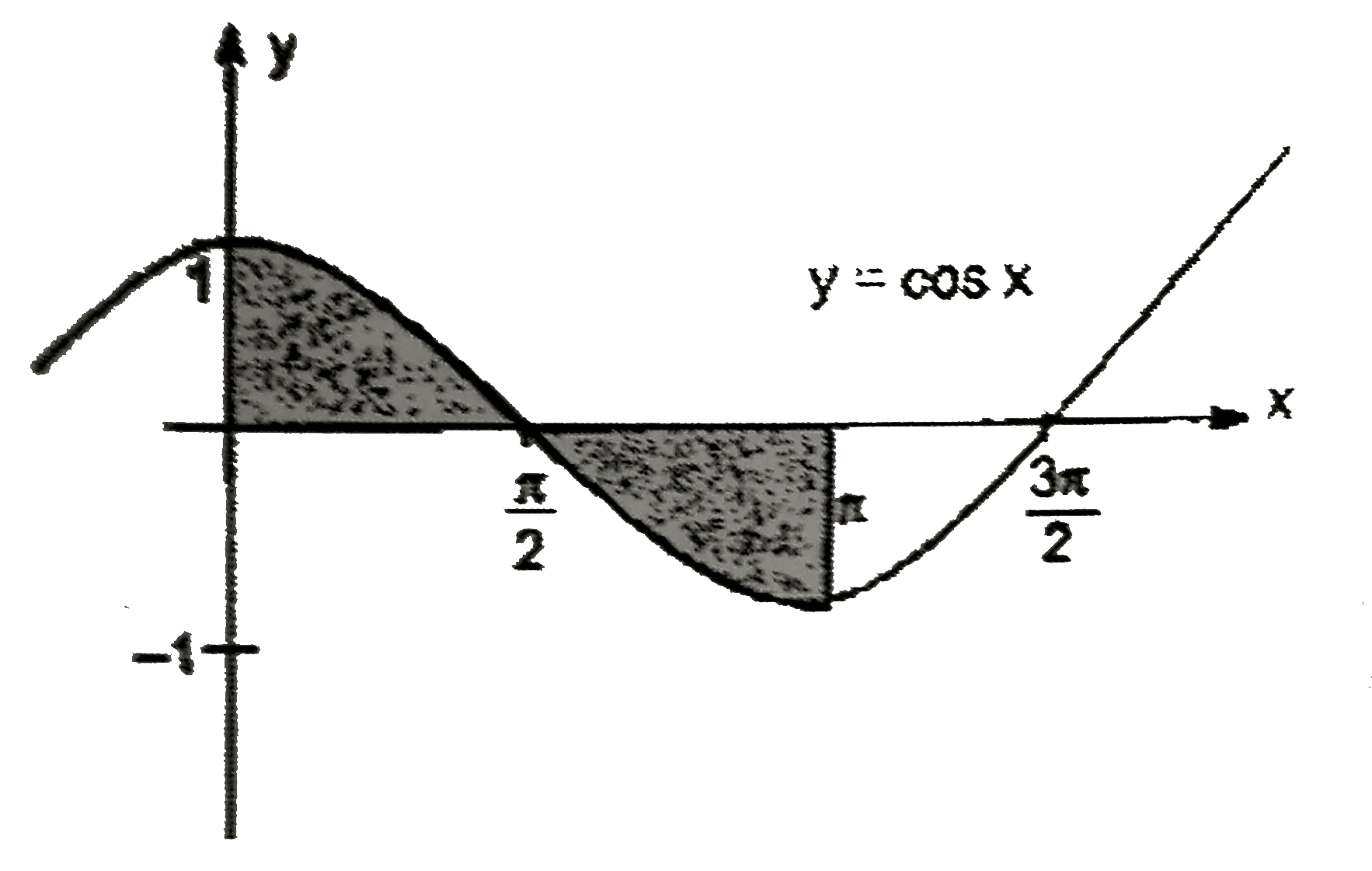
(a). Find the area under the curve `y=cosx` over the interval `[0,pi//2]` and `[0,pi]`
View SolutionEvaluate
`int_(0)^(3)(x^(3)-6x)dx`
View SolutionFind `int_(0)^(2)(2x^(3)-6x+(3)/(x^(2)+1))dx`
View SolutionEvaluate `underset(1)overset(9) ((2t^(2)+t^(1/2)sqrt(t)-1)/(t^2)dt)`
View SolutionA particle moves along a line so that its velocity at time t is
`v(t)=t^(2)-t-6` (measured in meters per second) ltbr. (a). Find the displacement of the particle during the time period `1letle4`
(b). Find the distance traveled dring this time period.
View SolutionFind the position function of a particle that moves with velocity `v(t)=cospit` along a coordinate line, assuming that the particle has coordinate `s=4` or time t=0.
View SolutionSuppose that a particle mvoes on a straight line so that is velocity at time `t` is `v(t)=(t^(2)-2t)m//s`.
(a). Find the displacement of the particle during the time interval `0 le t le 3`
(b). Find the distance traveled by the particle during the time interval `0 le t le 3`.
View Solution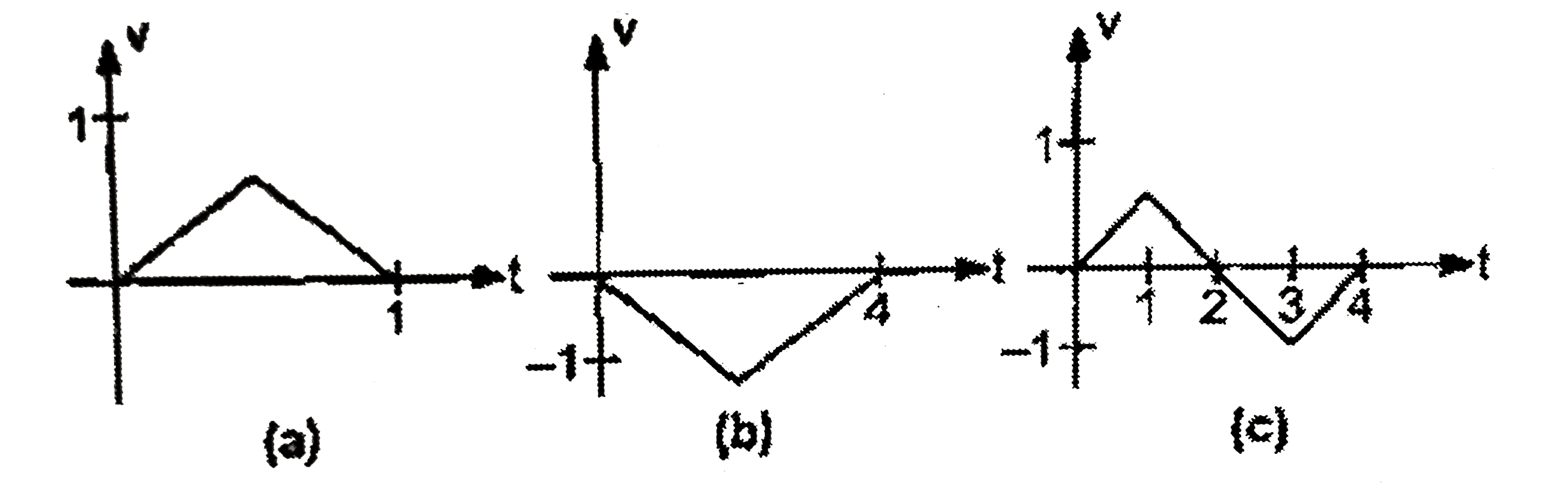
Fig. shows thre velocity versus time curves for a particle in rectilinear motionalong a horizontal line. In each case, find the displacement of the particle over the time interval `0 le t le 4`, and explain what it tells you about the motion of the particle.
View Solution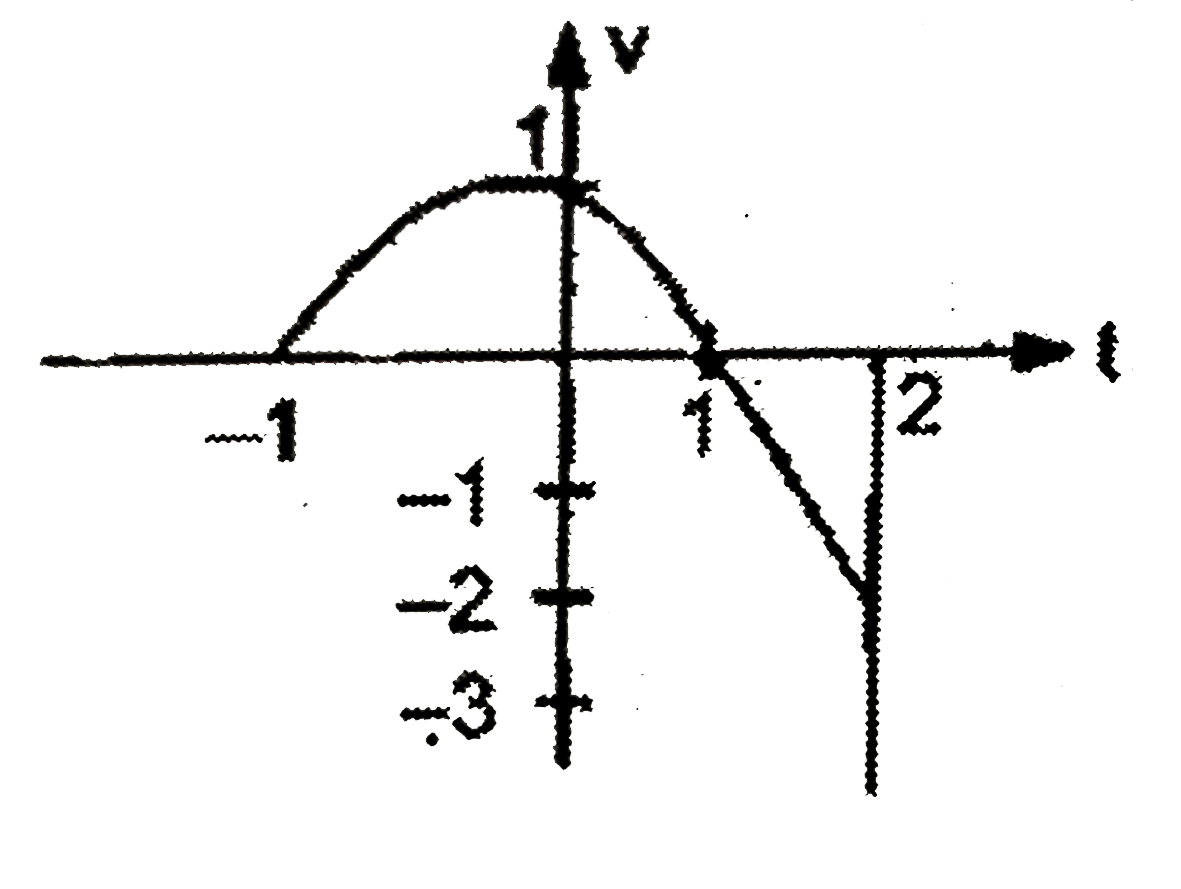
find the total area between the cuve `y=1-x^(2)` and the x-axis over the interval [0,2] (fig).
View Solution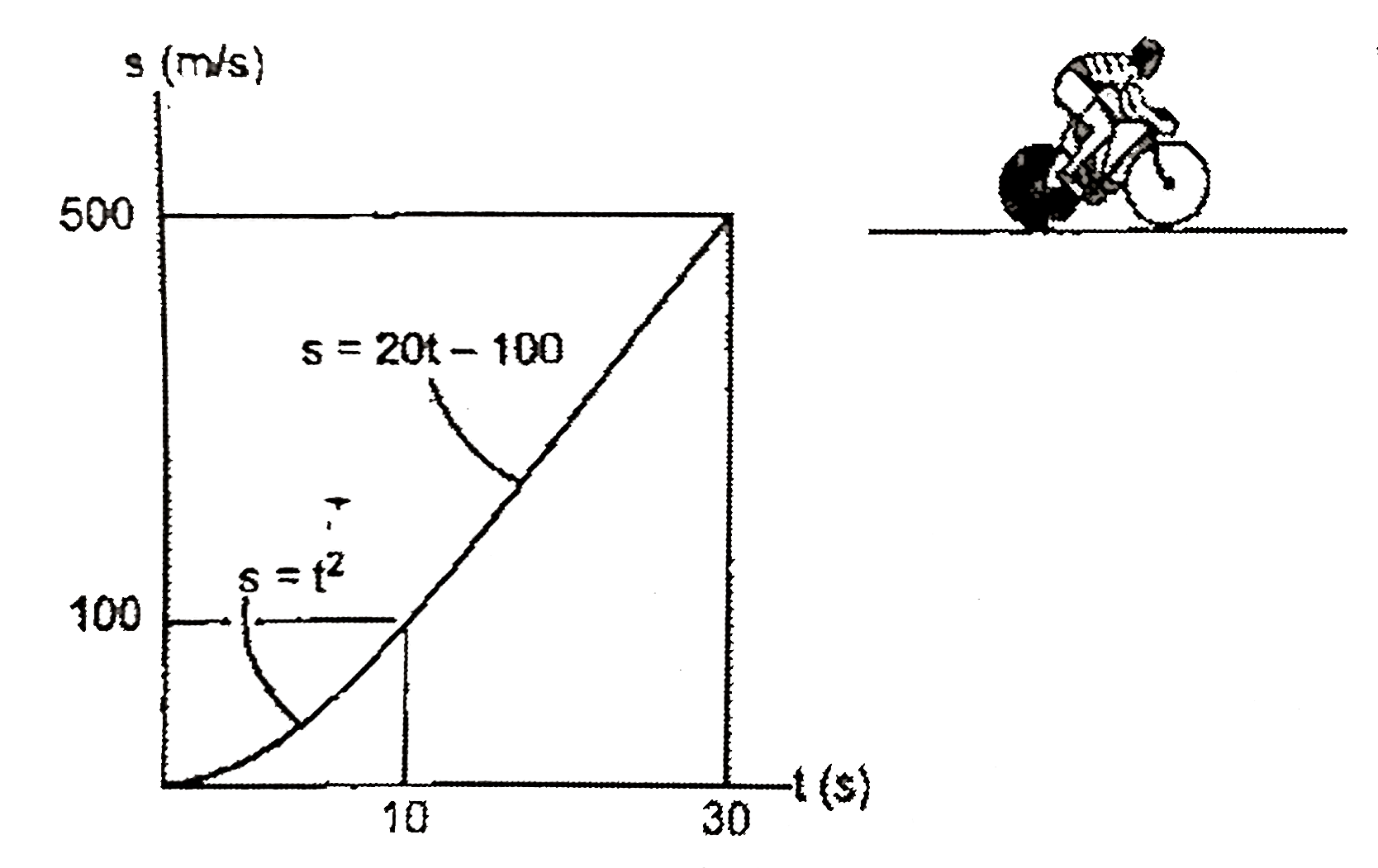
A bicycle moves along a stragith road such that its construct the v-t and a-t graphs for `0 le t le 30`.
View SolutionAn experimental car in fig (a) starts from rest and travels along a straight track such that it accelerates at a constant rate for 10 s and then decelerates at a constant rate draw the v-t and s-t graphs and determine the time t' needed to stop the car. how far has the car travelled.?
View SolutionGiven `a=4-2t`, initial velocity at `t=0,u=5,` find distance travelled till 12 sec.
View SolutionIf a particle with `a = kv^(2)` and initial velocity is u then velocity after S displacement. Here `k` is a constant
View SolutionGiven `a=-cost,` at `t=0,u=0,x=1`
Position at `t=pi`
Find distance from 0 to `2pi`.
View SolutionA particle moves along x-axis with acceleration `a=6(t-1)` where t is in second. If the particle is initially at the origin and it moves along positive x-axis with `v_(0)=2m//s`, find the nature of motion of the particle.
View SolutionA particle moves alo g a straight line and its velocity depends on time as `v=6t-3t^(2)` where 'v' is in m/sec and 't' is in sec. find average velocity and average speed forr first four seconds.
View SolutionVelocity vector of a particle is given as
`vecv=4thati+3hatj`
At t=0 position of the particle is given as `vecr_(0)=2hatj`
Find the position vector of the particle at t=2 sec and te average acceleration of the particle for t=0 to t=2sec.
View SolutionGiven that `x=120-15t-6t^(2)+t^(3)(tgt0)`, find the time when the velocity is zero. Find the displacement at this instant.
View Solution(The figure shows the (V,t) graph for the train .accelerating' ifrom resi up to a maximum speed of `Vms-1.` and then decelerating to a speed of `10ms^(-1)`The acceleration and deceleration. have , the same magnitude which is equal to `0.5 m//s`
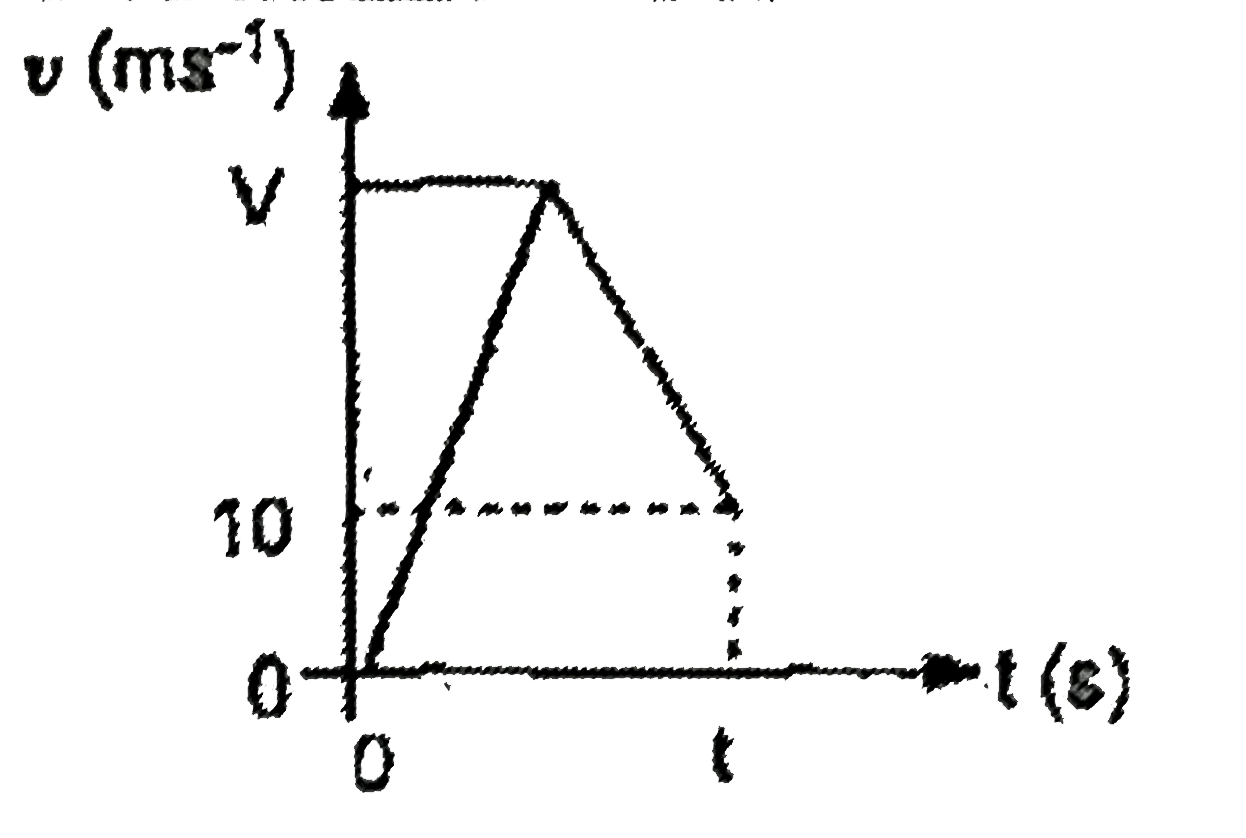
show that the distance travelled is `(2V^(2)-100)` metre
View SolutionThe velocily-time graph for a particle travelling along a straight line is.shown in the Fig. 1E:61. Find
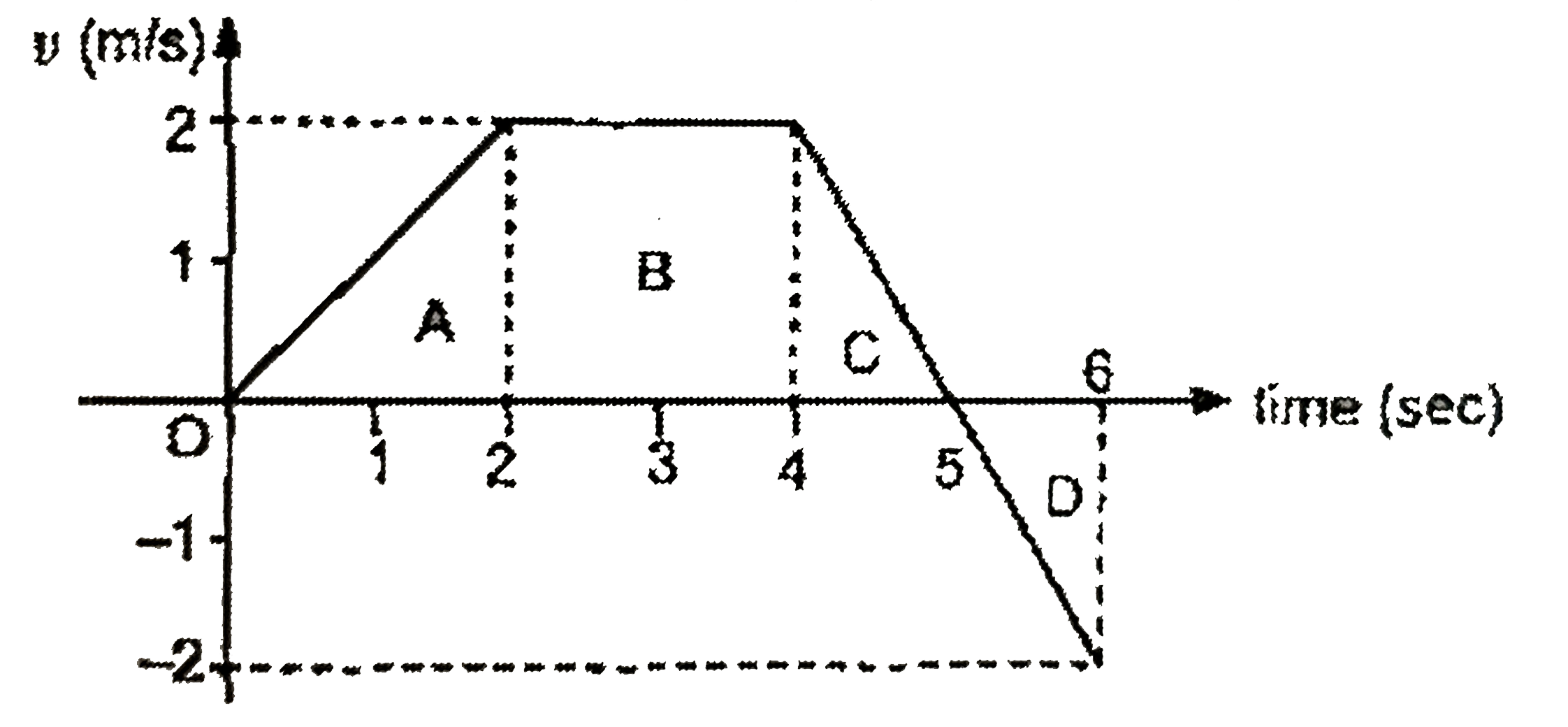
(a). distance travelled from zero to 6 sec.
displacement in the above time interval
View SolutionA bird flies for 4s with a velocity `V=(t-2) m//s` in a straight line where t= time in second Calculate the displacement and distance covered by the bird
View SolutionA particle moves in such a way that its position vector at any time `t "is" `t "is" hati+`1/2 t^(2) hatj + thatK` Find a function of time (a) the velocity, (b) the speed, (c) the acceleration, (d) the magnitude of the acceleration, (e) the magnitude of the component of acceleration along velocity (called tangential' acceleration), (f) the magnitude of the component ofacceleration perpendicular to velocity (called normal acceleration).
View SolutionA particle moves in xy plane with a velocity given by `vecV = (8t-2)hati+2hatj.`. If it passes through the point `(14,4)` at `t=2 sec , then give eqution of the point
View SolutionFirst, an auto starts from rest and accelerates uniformly for 15 s acquiring a velocity of `30m//s.` Secondly, the auto then moves:at this constant velocity of `30 m//s` for the next 15 s, after which thirdly, the auto decelerates uniformly by braking at `1.5 m// s^(2)` until it stops.
(a) Sketch the velocity-time graph.
(b) Sketch the acceleration-time graph for auto
(c) Sketch displacement-time graph for auto
View SolutionA particle having a velocity `v = v_0` at `t= 0` is decelerated at the rate `|a| = alpha sqrtv ,` where `alpha` is a positive constant.
View SolutionA particle travels so that its acceleration is given by `vec(a)=5 cos t hat(i)-3 sin t hat(j)`. If the particle is located at `(-3, 2)` at time `t=0` and is moving with a velocity given by `(-3hat(i)+2hat(j))`. Find
(i) The velocity `[vec(v)=int vec(a).dt]` at time t and
(ii) The position vector `[vec(r)=int vec(v).dt]` of the particle at time `t (t gt 0)`.
View Solution(i) A particle is moving in three dimensions.Its position vector is given by
`vecr=6hati+(3+4t)hatj-(3+2t-t^(2))hatk`
Distance are in meters, and the time t, in seconds.
( a) What is the velocity vector at `t = + 3 ?`
(b) What is the speed `("in" m//"sec") at. t = + 3` ?
(c) What is the acceleration vector and what is its magnitude `("in m"//"sec"^(2)) at.t = +3`?
(ii) Now the particle is moving only along the z-axis, and its position is given by `(t^(2)- 2t -3)hatk` k at what time does the particle stand still? _
View SolutionA body projected vertically upward from the top of a tower reaches the ground in itme `t_(1).` If it is projected vertically downwards from the same position with the same velocity , it reaches the ground in time `t_(2)`. If a body is released from rest and from the same position then what will be the time (t) required by body to reach the ground?
View SolutionA body falls from same height and return back to initial position Draw displacement `hat(s)`-time (t), distance (s) - time (t) and velocity `hat(V)`-time (t), speed (v), time (t) and acceleration `hat(a)`-time (t) graphs for the motion of the body
View SolutionA boy throws a ball vertically upward with an initial speed of `15.0m//s`.The ball was released when it was at `2.00`m above ground. The boy catches it at the same point as the point of projection
(a) What is maximum height reaches by the ball ?
How long is the ball in the air?
View SolutionA man standing in an elevator observes a screw fall from the ceiling. The ceiling is 3 m above the floor.
(a) If the elevator is moving upward with a speed of 2.2`m//s` how long does it takes for the screw to hit the floor?
(b) How long is the screw in air if the elevator starts from rest when the screw falls and moves upwards with a constant acceleration of `a=4.0m//s^(2)`?
View SolutionA speeder moves at a constant `15m//s` in a school zone A police car starts from rest just as the speeder passed it.The police car accelerates at.`2 m//s^(2)` until it reaches its.maximum velocity of `20 m//s.`Where and when does the speeder get caught ?
View Solutiontwo cars approach each other on a straight road. Car A moves at `16 m//s` and car B moves at `8m//s.` When they are `45 m` apart both drivers apply their brakes. Car A slows down at .`2 m//s^(2)` . While car B slows down at `4 m//s^(2)`. Where and when do they collide?
View SolutionA circular wire frame is fixed in a vertical plane. A smooth wire is tightly stretched between point `P_(1)"and"P_(2)`. A bead slides from the point `P_(1)` the highest point of the circle Determine (a) its velocity v when it arrives at `P_(2)` and (b) show that time to slide along any similar chord is same

View SolutionA car is speeding at `25 m//s` in a low speed zone .A police car starts from rest just as the speeder passes and accelerates at a constant rate of `5m//s^(2)`
(a) When does the police car catch the speeding car?
(b) How fast in the police car travelling when it catches up with the speeder ?
How for have the cars travelled when the police car catches the speeder?
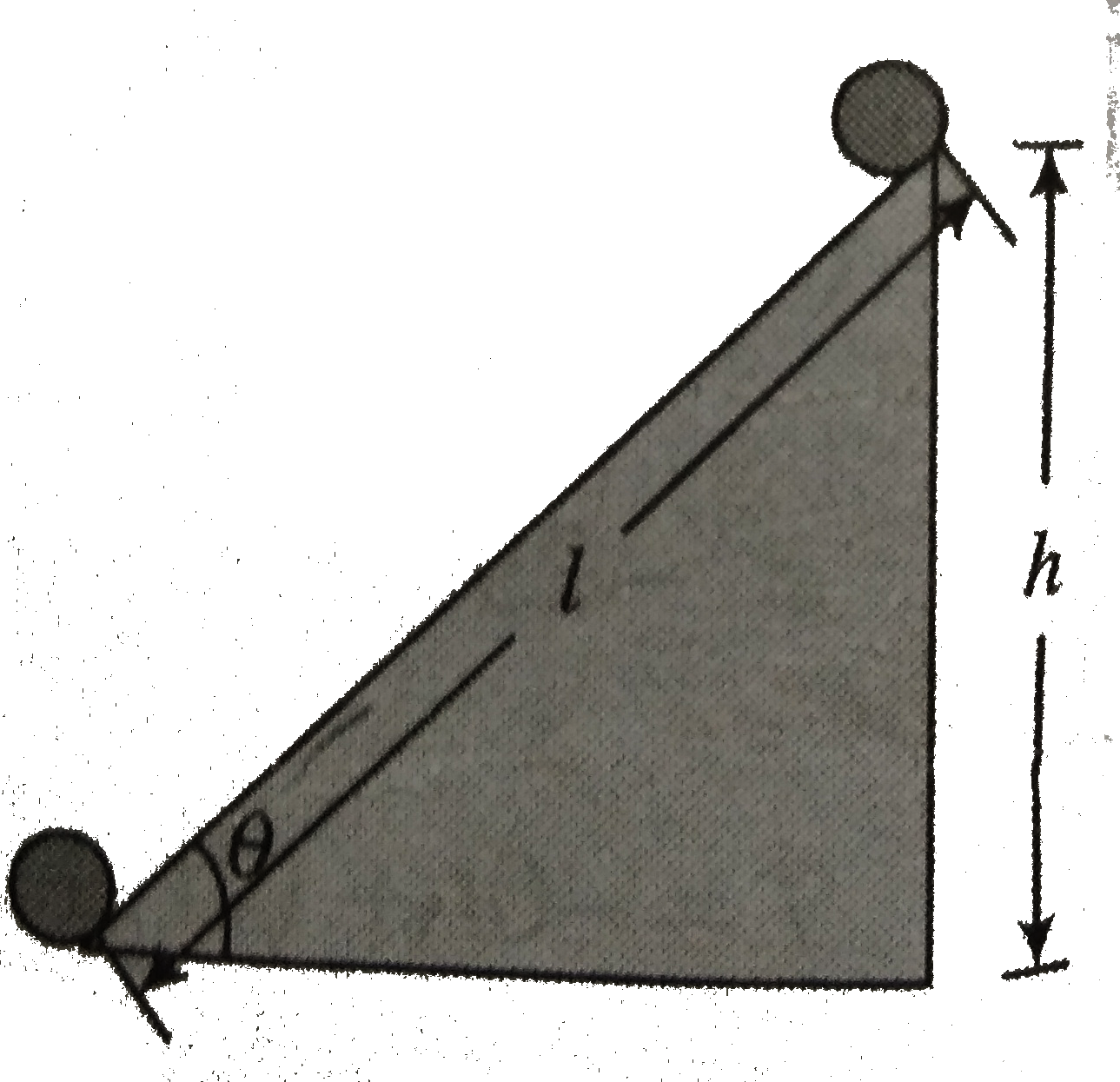
View SolutionBall `1` is released from the top of a smooth inclined plane, the at the same instant ball `2` is projected from the foot of the plane with such a velocity that they meet halfway up the incline. Determine:
a.the velocity with which balls are projected and
b. the velocity of each ball when they meet.
 .
.
View SolutionThe velocity of a particle at `t=0 "is"vecU = 4hati+3hatj"m"//"sec"` and a constant acceleration is `veca=6hati+4hatj"m"//"sec"^(2)`. Find the velocity and displacement of the particle at `t=2 sec.`
View SolutionThe acceleration of a moving body at any time 't' is given by `veca=(4t)hati+(3t^(2))hatj" ""m"//"sec"^(2).If vecU=0` then find the velocity of the prticle at 4 sec.
View SolutionA particle of mass 1 kg has a velocity of `2m//s`. A constant force of 2N acts on the particle for 1s in a direction perpendicular to its initial velocity. Find the velocity and displacement of the particle at the end of 1 s.
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows `u_(x) = 3m//s,u_(y)=4m//s,a_(x)=2m//s^(2)"and"a_(y)=1m//^(2).` The rate of change of speed at this moment is
`(a) 4.m//s^(2)`
`(b) 2,m//s^(2)`
`(c) sqrt3.m//s^(2)`
`(d) sqrt5 .m//s^(2)`
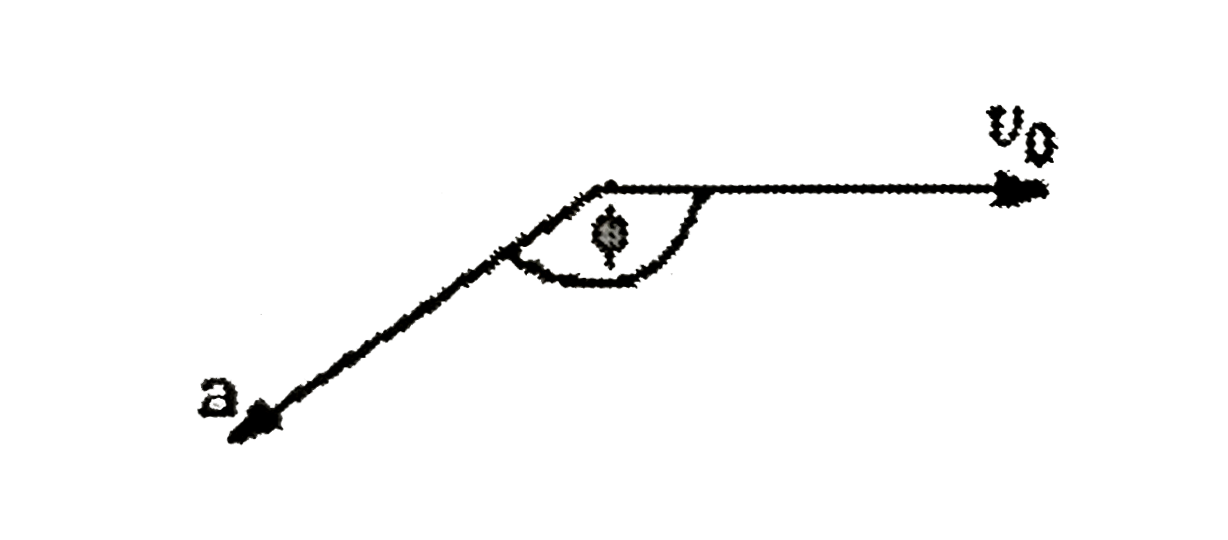
View SolutionThe figure shows the velocity and the accelerationl of a point-like body at the initial moment of its motion. The direction and the absolute value of the acceleration remain constant.Find the time in seconds when the velocity reach its minimum value?
`("Data" : a=6m//^(2), v_(0)=24m//s,phi=143^(@))
View SolutionA footballer throws a ball from a height of 2.00m above the ground with an initial velocity of `20.0m//s` at an angle of `30^(@)` above the horizontal (a) How long does the ball take to cross the goal line `32.0m` from the point of release?(b) What is the ball's height above the ground as it crosses the goal line?
View SolutionA bomber is moving horizontally at a speed `v_(1)=72m//s` at a height of `h=103m.` An enemy tank is moving horizontally `(x-axis)` with constant spedd . At the instant the bomb is released a tank is at a distance `x_(0)=125m` from origin. Origin is directly below a bomber at the instant of release of bomb. Assurning the tank to be 3 m high find the velocity `v_(2)` and the time of flight of bomb.

View SolutionA boy throws a ball with velocity `v_(0) =10sqrt2 m//s` at an angle of `45^(@)` as shown in the figure .After collision with the ball the vertical component of ball's velocity is unchanged and the horizontal. Component is reversed in direction .Where does the ball hit the ground?
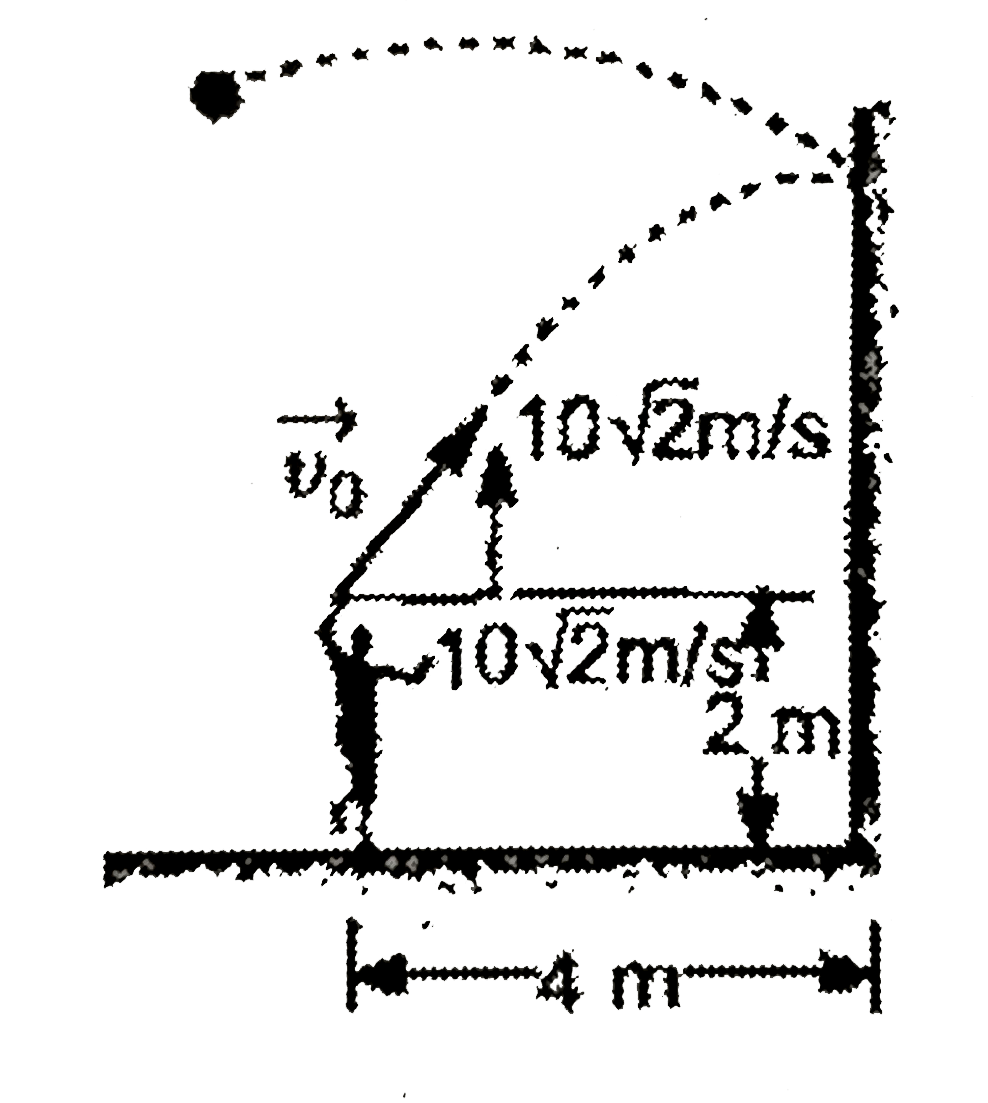
View SolutionA policeman is in pursuit of a thief Both are running at `5m//s`. Suddenly they come across a gap between building as shown in figure. The thief leaps at `5m//s` and at `45^(@)` while the policeman leaps horizontally.
(a) Does the policeman clear the gap ?
(b) BY how much does the thief clear the gap ?
View SolutionA helicopter is flying at 100m and flying at `25m//s` at an angle `37^(@)` above the horizontal when a package is dropped from it ,
(a) Where does the package land ,
(b) If the helicopter flies at constant velocity where is it when the package lands?

View SolutionA particle is projected from the origin in such a way that it passes through a given point P (a, b} What is the minimum requrired speed to do so?
View SolutionA bullet with muzzvelocity 100 m/s is to be shot at a target 30 m away in the horizontal line .How high above the target must the renaimed so that the bullet will hit the target?

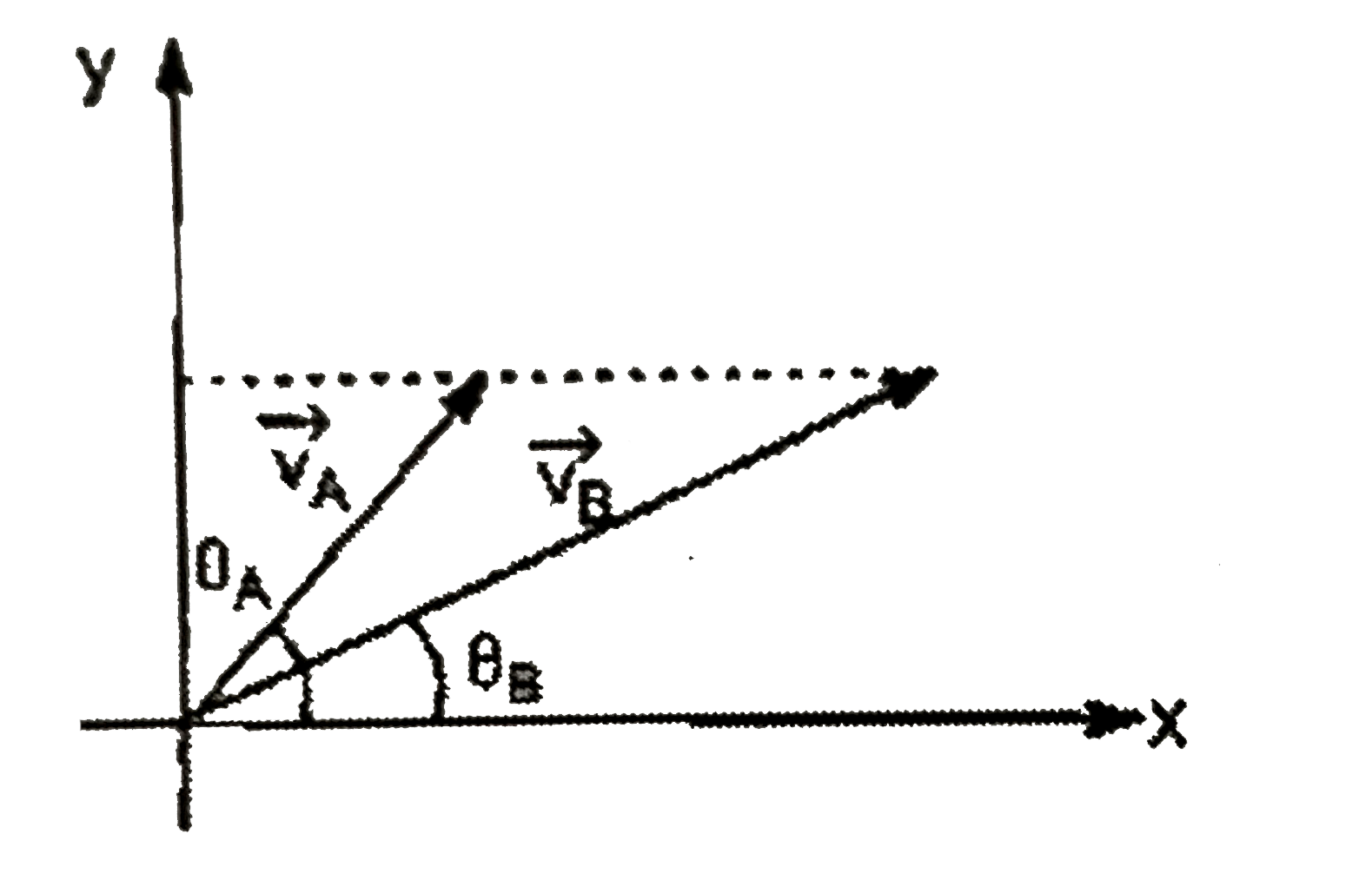
View SolutionIwo particles A & B are projected from the same point in, different directions in such a manner that vertical components of their initial velocities are same :
(a) Find ratio of time of flight
(b) Find ratio of range.
View SolutionFour cannon balls, `(1),(2),(3), and (4)` are fired from level ground. Cannon ball (1) is fired at an angle of `60^@` above the horizontal and follows the path shown in (Fig. 5.9).
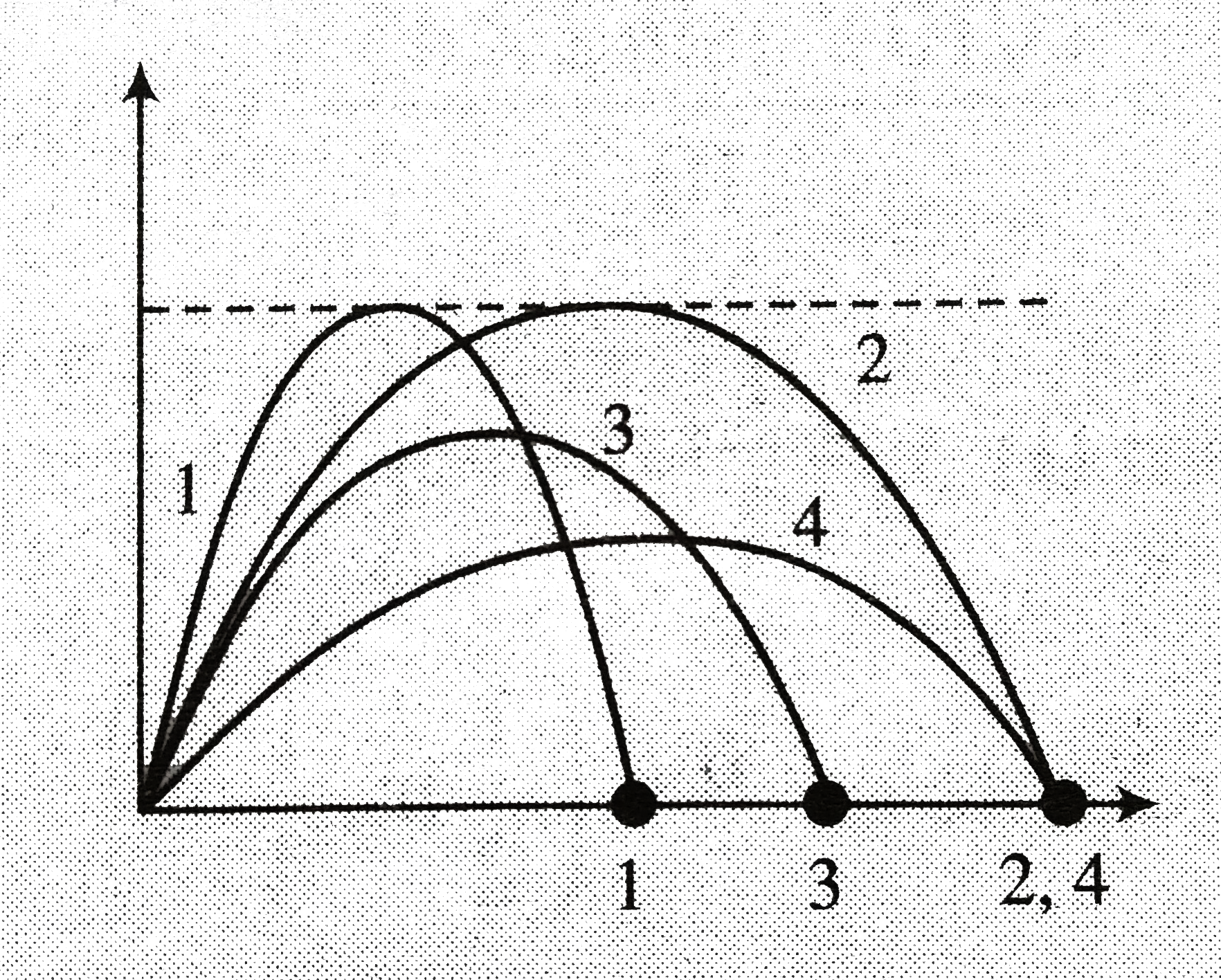 .
.
Cannon balls (2) and (3) are fired at angle of `45^@` and (4) is fired at an angle of `30^@` above the horozontal. Which cannon ball has the largest initial speed ?
View SolutionA particle is projected from origin in xy-plane and its equation ,of trajectory is given by `y = ax - bx^(2)`. The only acceleration ,in the motion is' f' which is constant and in `-ve` direction of, y-axis.
(a) Find the velocity of projection and the angle of projection.
(b) Point of projection is considered as origin and x-axis along the horizontal ground. Find the horizontal range: and maximum height of projectile. Projectile completes its flight in horizonal plane of projection.
View SolutionA gun is mounted on a plateau 960 m away from its edge as shown. Height of plateau is 960 m The gun can fire shells with a velocity of 100 m/s at any angle. Of the following choices, what is the minimum distance (OP)x from the edge of plateau where the shell of gun can reach?

View SolutionTwo particles were projected one by one with the same initial velocity from the same point on level ground. They follow the same parabolic trajectory and are found to be in the same horizontal level, separated by a distance of `1 m, 2 s` after the second partice was projected. Assume that the horizontal component of their velocities is `0.5 ms^-1`. Find
(a) the horizontal range of the parabolic path.
(b) the maximum height for the parabolic path.
View SolutionA projectile is fired with velocity `v_(0)` from a gun adjusted for a maximum range.It passes through two points `P` and `Q` whose heights above the horizontal are `h` each.The separation of the two points is
View SolutionA fighter plane is flying horizontally at a height of `250m` from ground with constant velocity of `500m//s`. It passes exactly over a cannon which can fire a shell at any time in any direction with a speed of `100m//s`. Find the duration of time for which the plane is in danger of being hit by a cannon shell.
View SolutionA shot is fired with a velocity `u` at a very high vertical wall whose distance from the point of projection is `x`.The greatest height above the level of the point of projection at which the bullet can hit the wall is.
View SolutionAn Aeroplane flies horizontaily at a height h at a speed v. An anti-air craft gun fires a shell at the plane when it is vertically above the gun. Show that the minimum muzzle velocity required to hit the plane is `sqrt(v^2+2gh)` at an angle `tan^(-1)((sqrt(2gh))/(v))`
View SolutionA particle is projected from a point on the level ground and its height is `h` when at horizontal distances `a and 2 a` from its point of projection. Find the velocity of projection.
View SolutionA man is riding on a flat car travelling with a constant speed of `10m//s`.He wishes to throw a ball through a stationary hoop `5 m` above the height of his hands in such a manner that the ball will move horizontally as it passes through the hoop. He throws the ball with a speed of `12.5 m//s` w.r.t himself.
How many seconds after he release the ball will it pass through the hoop?
View SolutionA heavy particles is projected from a point at the foot of a fixed plane, inclined at an angle `45^(@)` to the horizontal, in the vertical plane containing the line of greatest slope through the point. If `phi(gt45^(@))` is the inclination to the horizontal of the initial direction of projection,for what value of `tan phi` will the particle strike the plane horizontal.
View SolutionThe angular elevation of an enemy's position on a hill 'h' ft height is `alpha`.What should be the minimum velocity of the projectile in order to hit the enemy?
View SolutionA projectile is thrown at an angle `theta` with an inclined plane of inclination `beta` as shown in fig. 1E108. Find the relation between `beta` and `theta` ifv :
(a)projectile strikezs the inclined plane perpendicularly,
(b) projectile strikes the inclined plane horizontal.
View Solution
Example questions and complete solutions for chapter DESCRIPTION OF MOTION of SHREE BALAJI PHYSICS (HINGLISH) of Class 11