Complete Solutions to Level-1 of chapter DESCRIPTION OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | DESCRIPTION OF MOTION |
| ANURAG MISHRA | Level-1 |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
It is possible to add five. unit vectors to get an unit vector, The statement is :
(a) True , (b) False
View SolutionIf a vector is rotated by angle `theta` then it is necessarily changed. The statement is :
(a) True , (b) False
View SolutionIt is possible to add n vectors of equal magnitude and get zero:
(True , (b) False
View SolutionIt is possible to add n vectors of different magnitude and get zero.
(a) True , (b) False
View SolutionIt is possible to have ` vec(a) xx vec(b)= vec(a). vec(b)` for some suitable selection of `vec(a)` and `vec(b)`. For example `vec(a)= vec(0)` . The statement is :
(a) True , (b) False
View SolutionIf `|vec(A )| = |vec(B)|` and ` vec(A) !=+- vec(B)` then angle between the vectors `(vec(A) +vec(B))` and ` (vec(A)-vec(B))` is :
View SolutionA vector of magnitude a is turned through angle `theta` . The magnitude of change in the vector is given by:
View SolutionWhich of the sets given below may represent the magnitudes of three vectors adding to zero?
View SolutionThe resultant of ` vec(a)` and ` vec(b)` makes `alpha` with `vec(a)` and `beta` with `vec(b)`, then (a,b represent magnitudes of respective vectors) :
View SolutionLet `vec(C)=vec(A) +vec(B)` :
View SolutionLet the angle between two non-zero vectors `vec(A)` and `vec(B)` be `120^(@)` and its resultant be `vec(C)` then:
View SolutionWhich of the following two statements is more appropriate?
(a) Two velocities are added using triangle rule because velocity is vector quantity.
(b) Velocity is a vector quantity because two velocities are added using triangle rule.
View SolutionVector `vec(a)` is increased by ` Delta vec(a)` . If increment in magnitude of `vec(a)` is greater than magnitude of increment vector then angle between `vec(a) ` and ` Delta vec(a)` is :
View SolutionA moter car is going due north at a speed of 50 km/h. It makes a `90^0` left turn without changing the speed. The change in the velocity of the car is about
View SolutionA person moving on earth's surface starts from north pole & moves 500 km towards south and then moves 1000 km towards east and then again moves 500 km towards north and stops. The displacement of the person is:
View SolutionA person moves 20 m towards north-east then moves 20 m towards west and then again moves 20 m towards north-east and stops. The magnitude of displacement of the person is:
View SolutionIf `vec(A),vec(B),vec(C)` are mutually perpendicular vectors then which of the following statements is wrong?
View SolutionThe velocity of a particle varies with time as per the law `vec(v)=vec(a) +vec(b)` t where `vec(a)` and `vec(b)` are two constant vectors. The time at which velocity of the particle at t=0 is :
View SolutionA plane is inclined at an angle `30^(@)` with horizontal. The component of a vector `vec(A)= -10k` perpendicular to this plane is: (here z-direction is vertically upwards)
View SolutionIf `vec(a_(1)) and vec(a_(2))`are two non-collinear unit vectors and if `|vec(a_(1)) + vec(a_(2))|=sqrt(3)`, then the value of `(vec(a_(1))-vec(a_(2))). (2 vec(a_(1))+vec(a_(2)))` is :
View SolutionIf `vec(A)=vec(B)+vec(C)` and the magnitude of `vec(A), vec(B) and vec(C)` are 5, 4, and 3 units respectively the angle between `vec(A) and vec(B)` is :
View SolutionThe sum of two forces at a point is 16N. if their resultant is normal to the smaller force and has a magnitude of 8N, then two forces are
View SolutionWhat is the component of `3 hat(i) +4 hat(j) "along" hat(i)+hat(j)`:
View SolutionAt what angle the vector `(vec(A)+vec(B))` and `(vec(A)-vec(B))` must act, so that the resultant is `sqrt(A^(2)_B^(2))`
View SolutionThe resultant of `vec(A) and vec(B)` is perpendicular to `vec(A)`. What is angle between `vec(A) and vec(B)` ?
View SolutionA particle moves through angular displacement `theta` on a circular path of radius' r'. The linear displacement will be:
View SolutionIf a vector `vec(A)` makes an angle `alpha , beta ` and `gamma ` with X,Y and Z axis respectively then `sin ^(2) alpha +sin^(2) beta +sin ^(2)gamma =....`
View SolutionThe X and Y - component of ` vec (p) ` are `7hat(i) and 6hat(j)`. Also , the X and Y-components of `vec(p)+vec(Q)` are `11 hat(i) and 9 hat (j)` respectively. Then magnitude of `vec(Q)` is :
View SolutionTwo vector `vec(A)=2 hat(i) +3hat(j)-4hat(k)` and `vec(B)=4hat(i) + 8hat(j) +x hat(k)` are such that the component of `vec(B) ` along `vec(A)` is zero . Then the value of x will be :
View SolutionTwo vector `vec(A)=3hat(i) +8 hat(j) -2hat(k)` and `vec(B)=6hat(i)+16 hat(j) +x hat(k)` are such that the component of `vec(B)` perpendicular to `vec(A)` is zero . Then the value of x will be :
View SolutionA blind person after Walking 10 steps in one direction, each of length 80cm, turns randomly to left or right, After walking 'n' steps, the maximum displacement of person is `16 sqrt(2)` .Then value of'n' is :
View SolutionTwo vectors `vec(A)` and `vec(B)` have magnitudes 2 and `2sqrt(2)` respectively. It is found that `vec(A).vec(B) = |vec(A) xx vec(B)|`, then the value of `|(vec(A)+vec(B))/(vec(A)-vec(B))|` will be :
View SolutionIf the resultant of two vectors having magnitudes of 7 and 4 is 3, then the magnitude of the cross product of the two vectors will be:
View SolutionThe adjacent sides of a parallelogram is represented by vectors `2hat(i)+3 hat(j)` and `hat(i) +4 hat(j)`. The area of the parallelogram is :
View SolutionThe maximum magnitude of cross product of two vectors is 12 units and the maximum magnitude of their resultant is 7 units, then their minimum resultant vector will be a:
View SolutionSix forces are acting on a particle. Angle between two adjacent force is `60^(@)`. Five of the forces have magnitude `F_(1)` and the sixth has magnitude `F_(2)` . The resultant of all the forces will have magnitude of:
View SolutionThe quantity `int_(t_(1))^(t_(2)) vec(V)`dt represents:
View SolutionLet`vec(V) =v_(x)hat(i)+v_(y)hat(j)+v_(z)hat(k)`, then `int_(t_(1))^(t_(2)) V_(y)` represents: (for the duration `t_(1) to t_(2))`
View SolutionA particle has a velocity u towards east at `t=0`. Its acceleration is towards west and is constant. Let `x_A` and `x_B` be the magnitude of displacements in the first 10 seconds and the next 10 seconds
View SolutionA stone is released from an elevator going up with an acceleration a. The acceleration of the stone after the release is
View SolutionA person standing near the edge of the top of a building throws two balls A and B. The ball A is thrown vertically upward and B is thrown vertically downward with the same speed. The ball A hits the ground with speed `v_A` and the ball B hits the ground wiht a speed `v_B`. We have
View SolutionA body travelling along a straight line , one thired of the total distance with a velocity ` 4 ms^(-1)`. The remaining part of the distance was covered with a velocity ` 2 ms^(-1)` for half the time and with velocity ` 6 ms^(-1)` for the other half of time . What is the mean velocity averaged over te whle time of motin ?
View SolutionTwo bullets are fired simultaneously, horizontally and with different speeds from the same place. Whch bullet will hit the ground first?
View SolutionTwo projectiles `A` and `B` are projected with an angle of projection `15^(@)` for the projectile `A` and `45^(@)` for the projectile `B`. If `R_(A)` and `R_(B)` be the horizontal range for the two projectiles, then
View SolutionIn the arrangement shown in figure the ends P and Q of an inextensible string move downwards with uniform speed u. Pulleys A and B are fixed. The mass M moves upwards with a speed

View SolutionThe Acelerations of a paerticle as seen from two frames `S_1 and S_2` have equal magnitude `4 m/s^2`.
View SolutionA train passes an observer standing on a platform. The first carriage of the train passes the observer in time `t_(1) = 1 s` and the second carriage in `t_(2) = 1.5s`. Find its acceleration assuming it to be constant. The length of each carriage is: l = 12 m.
View SolutionThe position vector of a particle varies with time as `overline(r)=overline(r_(0))t(1-alphat)` where `overline(r)_(0)` is a constant vector and `alpha` is a positive constant. The distance travelled by particle in a time interval in which particle returns to its initial position is `Kr_(0)//16alpha`. Determine the value of `K`?
View SolutionA particle traversed on third of the distance with a velocity `v_(0)`, the remaining part of the distance was covered with velocity `v_(1)` for half the time and with a velocity `v_(2)` for the remaining half of time. Assuming motion to be rectilinear, find the the mean velocity of the particle averaged over the whole time of motion.
View SolutionA point moves in xy-plane according to equation x = at, y = at (l - bt) where a and b are positive constants and t is time. The instant at which velocity vector is at `pi//4` with acceleration vector is given by:
View SolutionA body starts from rest at A and moves with uniform accelerationa in a straight line. T seconds after,a second body starts from A and moves with uniform velocity Kinthe same line. Prove that the second body will be ahead of the first for a time `(2)/(a) sqrt(V (V - 2 aT))`
View SolutionA particle is moving in the x-y plane. At certain instant of time, the components of its velocity and acceleration are as follows: `v_(x)=3ms^(-1), v_(y)=4ms^(-1), a_(x)=2ms^(-2) and a_(y)=1ms^(-2)`. The rate of change of speed at this moment is
View SolutionTwo cars start off to race with velocities `4 m/s and 2 m/s` and travel in straight line with uniform accelerations `1 msec^-2`and 2 msec − 2` respectively. If they reach the final point at the same instant, then the length of the path is.
View SolutionThe instantaneous velocity of a particle moving in xy-plane is `vecV=(ay)hati+(V_(0))hatj` where y is the instantaneous y co-ordinat of the particle and `V_(0)` is the particle starts from origin then its trajectory is
View SolutionAn open lift is coming down from the top of building at a constant speed `v=10m//s`. A boy standing on the lift throws a stone vertically upwards at a speed of 30 m/s w.r.t. himself. The time after which he will catch the stone is:
View SolutionA particle moving with uniform acceleration from `A` to `B` along a straight line has velocities `v_(1)` and `v_(2)` at `A` and `B` respectively. If `C` is the mid-point between `A` and `B` then determine the velocity of the particle at `C` .
 .
.
View Solutiona point source of light is rotating in a horizontal plane at a speed of `omega` radians/second. There is a wall at a distance d from the source. At some instant the focus of the light is at P and `angleSPN=theta` (see figure). Speed of the focus at this instant in terms of `theta` is

View SolutionWhen a body is thrown up in a lift with a velocity `u` relative to the lift, the time of flight is found to be `t`. The acceleration with which the lift is moving up is
View SolutionA block is kept on the floor of an elevator. The elevator starts descending with an acceleration of 12`m//s^(2)` the displacement of the block during `1^(st)` one second wth respect to elevator is-
View SolutionA point moves in a straight line so its displacement `x` meter at time `t` second is given by `x^(2)=1+t^(2)`. Its acceleration in `ms^(-2)` at time `t` second is .
View SolutionTwo particles start moving from the same point along the same straight line. The first moves with constant velocity `v` and the second with constant acceleration `a`. During the time that elapses before the sound catches the first, the greatest distance between the particle is.
View SolutionA ball is thrown up with a certain velocity at angle `theta` to the horizontal. The kinetic energy varies with height h of the particle as:
View SolutionA ball is thrown up with a certain velocity at an angle `theta` to the horizontal. The graph between kinetic energy and horizontal displacement is given by:
View SolutionA particle is thrown up with a ccrtain velocity and at an angle 0 with the horizontal. The variation of kinetic energy with time is given by :
View Solutionthe velocity of a particle varies with time as shown below the distance travelled by the travelled by the particle during `t=2s"and" t= 6s. Is

View SolutionFrom a high tower at time `t=0,` one stone is dropped from rest and simultaneously another stone is projected vertically up with an initial velocity the graph between distance betweeen the particles and time before either hits the ground is :
View SolutionA particle moves with constnat acceleration in the positive x-axis. At `t=0,` the particle is at and is at rest, then correct grahp between velocity and displacement is:
View SolutionA particle moves with constant acceleration a in the positive x-axis. At `t=0` the particle is at origin is at rest , then correct graph between `("velocity")^(2)` and displacement is :
View SolutionA particle is projected from gound At a height of 0.4 m from the ground, the velocity of a projective in vector form is `vecv=(6hati+2hatj)m//s` (the x-axis is horizontal and y-axis is vertically upwards). The angle of projection is `(g=10m//s^(2))`
View SolutionA particle moves in `x-y` plane according to the law `x = 4 sin 6t and y = 4 (1-cos 6t)`. The distance traversed by the particle in 4 second is (`x & y` are in meters)
View SolutionA swimmer crosses a flowing stream of width `omega` to and fro in time `t_(1)`. The time taken to cover the same distance up and down the stream is `t_(2)`. If `t_(3)` is the time the swimmer would take to swim a distance `2omega` in still water, then
View SolutionThe trajectory of a particle is as shown here and its trajectory follows the eqution `y=(x-1)^(3)+1.`Find co-ording of the point A on the curve such that direction of instantaneous velocity at A is same as direction of average velocity for the motion O ti A:
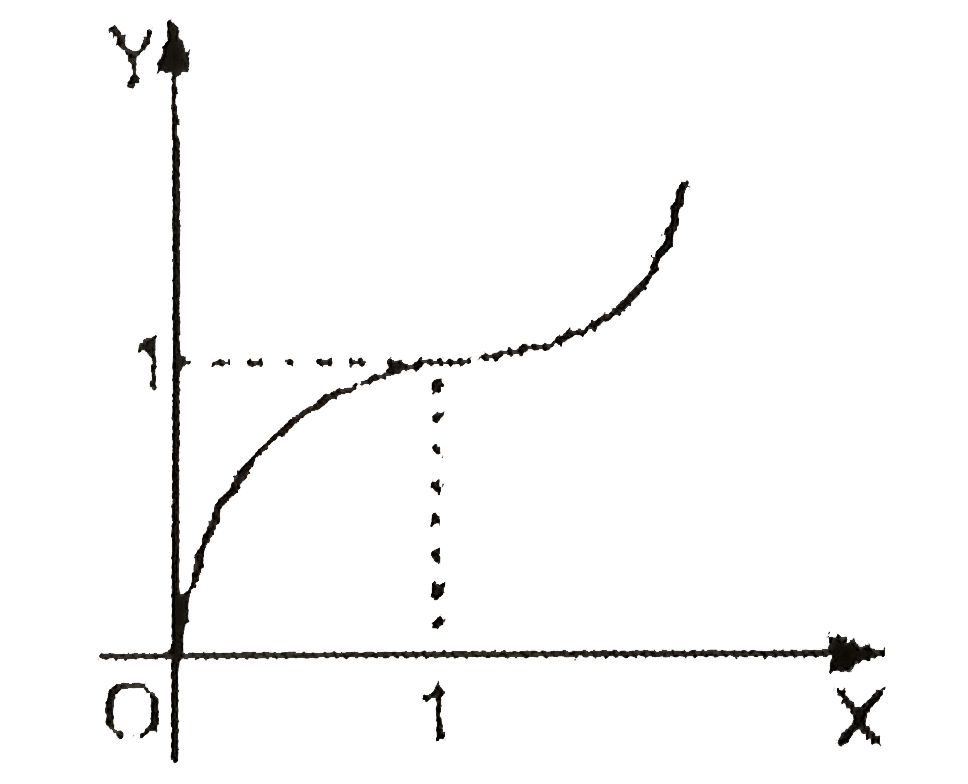
View SolutionA bird flies for 4 seconds with a velocity of `|t-2|m//sec.` In a straight line, where `t=` time in seconds. It covers a distance of
View SolutionA particle has an initial velocity of `9m//s` due east and a constant acceleration of `2m//s^(2)` due west. The displacement coverd by the particle in the fifth second of its motion is :
View SolutionA body is thrown vertically upwards from `A`. The top of a tower . It reaches the ground in time `t_(1)`. It it is thrown vertically downwards from `A` with the same speed it reaches the ground in time `t_(2)`, If it is allowed to fall freely from `A`. then the time it takes to reach the ground.
 .
.
View SolutionA hollow vertical cylinder of radius R and height h has smooth internal suface. A small particle is placed in contact with the inner side of the upper rim at a point P. It is given a horizontal speed `v_(0)` tangential to rim. It leaves the lower rim point Q vertically below P. The number of revolutions made by the particle will:
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the initial moment the particles were located over a tower at one point and moved with velocities `v_1 = 3m//s and v_2= 4m//s` horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular.
View SolutionA particle is projected vertically upwards from the ground with a speed V and a speed v and a second particle is projected at the same instant from a height h directly above the first particle with the same speed v at an angle of projection `theta` with the horizontal in upwards direction. The time when the distance between them is minimum is
View SolutionThree particles start from origin at the same time: one with velocity `v^(1)` along positive x-axis, the second along the positive y-axis with a velocity `v^(2)` and the third along the line y = x with such a speed that all the three always stay in a straight line, then velocity of the third particles is:
View SolutionA particle is projected from the ground at an angle of `60^(@)` with horizontal at speed `u = 20 m//s.` The radius of curvature of the path of the particle, when its velocity. makes an angle of `30^(@)` with horizontal is :
`(g=10 m//s^(2)`
View SolutionTwo particles are projected from the same point on ground simultaneously with speeds and `20m//s and 20//sqrt3` at angles `30^(@)` and `60^(@)` with the horizontal in the same direction.The maximum distance between them till both of them strike the ground is approximately `(g=10m//s^(2))`
View SolutionA rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
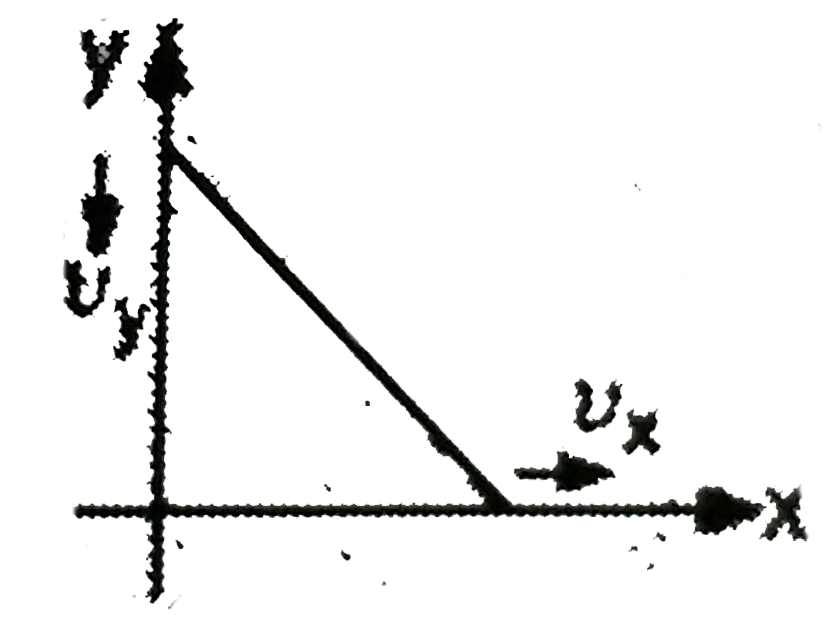
View SolutionA boy throws a ball upward with velocity `v_(0)=20m//s`. The wind imparts a horizontal acceleration of `4m//s^(2)` to the left. The angle `theta` at which the ball must be thrown so that the ball returns to the boy's hand is : `(g=10ms^(-2))`
View SolutionPosition vectors of a particle moving in xy plane at time t is `vecr=a(1-cos ometat)hati+asin omegat hatj`. The path of the particle is
View SolutionA particle moves in xy-plane. The position vector of particle at any time is `vecr={(2t)hati+(2t^(2))hatj}m.` The rate of change of `theta` at time `t = 2` second. ( where 0 is the angle which its velocity vector makes with positive x-axis) is :
View SolutionVelocity versus displacement graph of a particle moving in a straight line is shown in figure. Corresponding acceleration versus velocity graph will be.
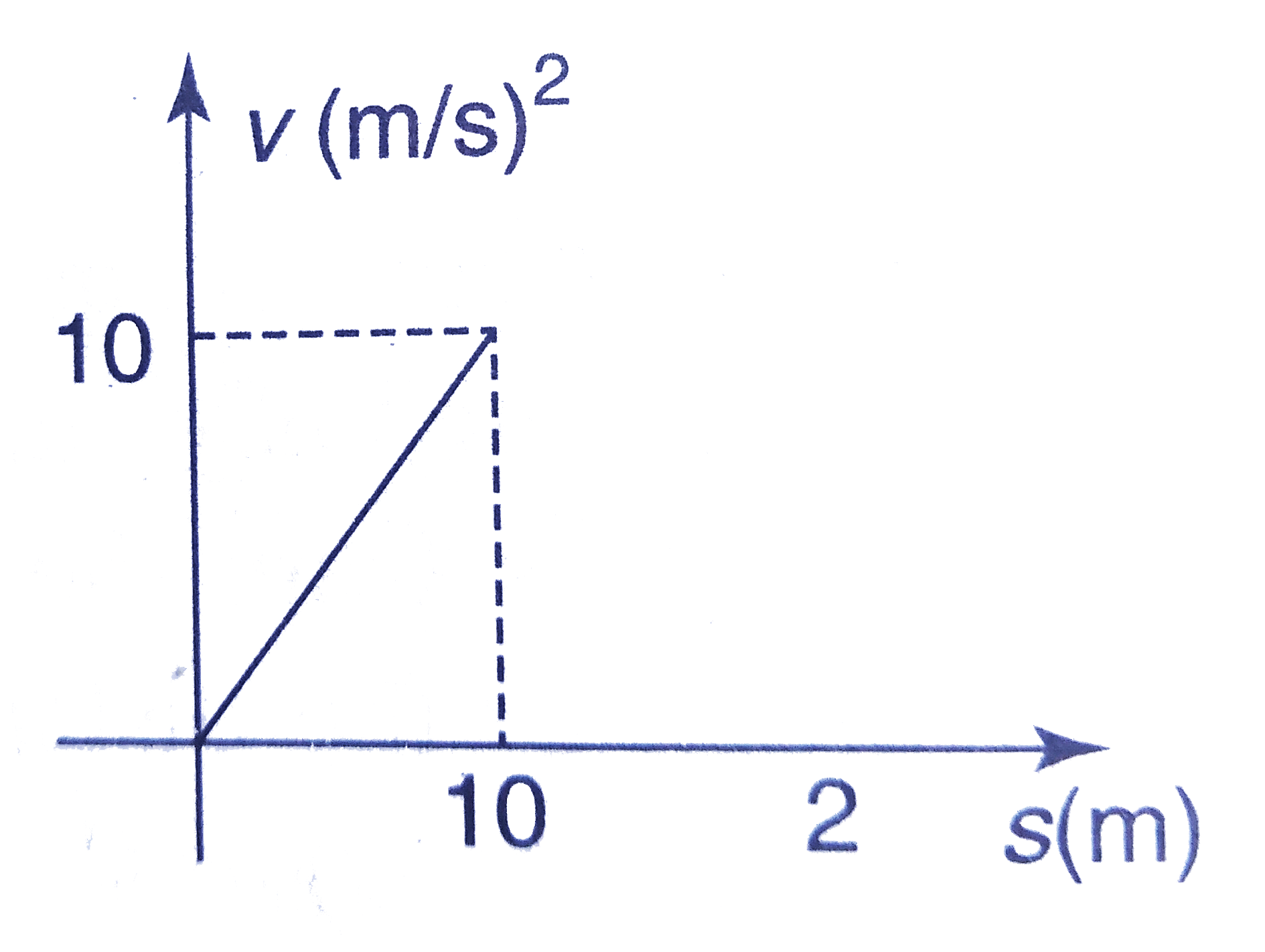
View Solution
Level-1 questions and complete solutions for chapter DESCRIPTION OF MOTION of SHREE BALAJI PHYSICS (HINGLISH) of Class 11