Complete Solutions to Level 2 of chapter KINETIC THEORY OF GASES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES |
| ARIHANT MASTER PROBLEM | Level 2 |
| Number Of Questions | 18 |
| Academic Year | 2023-24 |
The rms speed of molecules of an ideal gas is `v_(rms)`. Obtain the expression for rms value of relative speed for all pair of molecules in a gas sample.
View SolutionOn a cold winter night you switch on a room heater to keep your room warm. Does it mean that the total energy of the air inside the room increases after you switch on the heater?
View SolutionA hypothetical gas sample has its molecular speed distribution graph as shown in the figure. The speed (u) and `(dN)/(du)` have appropriate units. Find the root mean square speed of the molecules. Do not worry about units.
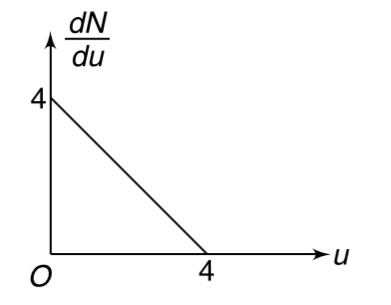
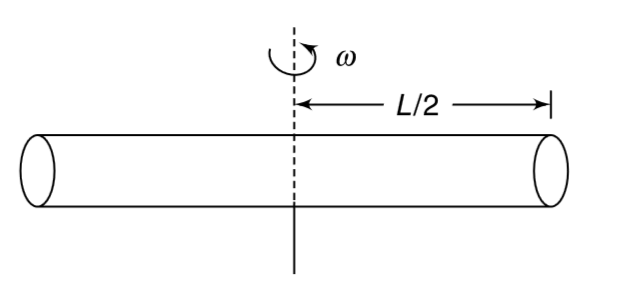
View SolutionA cylindrical container of length 2 L is rotating with an angular speed w about an axis passing through its centre and perpendicular to its length. Its contains an ideal gas of molar mass M. Calculate the ratio of gas pressure at the end of the container to the pressure at its centre. Neglect gravity and assume that temperature of the gas throughout the container is T.
View SolutionA container of volume V = 16.6 litre contains a mixture of hydrogen and helium at a temperature of 300 K. The pressure in the container is `6 x× 10^(5)` Pa and mass of the mixture is 10 g. Let `f_(1) " and " f_(2)` be the number of collisions made by the hydrogen and helium molecules with unit area of the container wall in unit time. Calculate the ratio `(f_(1))/(f_(2))`.
`[R = 8.3 "J mol"^(–1) K^(–1)]`.
View SolutionAn ideal gas is enclosed in a cylinder having cross sectional area A. The piston of mass M has its lower face inclined at `theta` to the horizontal. The lower face of the piston also has a hemispherical bulge of radius r. The atmospheric pressure is `P_(0)`.
(a) Find pressure of the gas.
(b) The piston is slowly pulled up by a distance x. During the process the piston is always maintained in equilibrium by adding heat to the gas. [It means if the piston is left at any stage it will stay there in equilibrium]. Find change in temperature of the gas. Number of mole of the gas in the cylinder is one.

View SolutionA beam of gas molecules is incident normally on a plate AB. Each gas molecule has mass m and velocity V. The incident beam falls on an area A on the plate and all the molecule strike the plate elastically. Number of molecules in unit volume of the beam is n. When the plate is moved to right (see fig.) a force `F_(1)` is needed to keep it moving with constant velocity u `(gt V)` . When the plate is moved to left with constant velocity u, an external force `F_(2)` is needed. Find `F_(2) – F_(1)`.

View SolutionAtmosphere of a planet contains only an ideal gas of molar mass `M_(0)`. The temperature of the atmosphere varies with height such that the density of atmosphere remains same throughout. The planet is a uniform sphere of mass M and radius ‘a’. Thickness of atmosphere is small compared to ‘a’ so that acceleration due to gravity can be assumed to be uniform throughout the atmosphere.
(a) Find the temperature difference between the surface of the planet and a point at height H in its atmosphere
(b) If the rms speed of gas molecules near the surface of the planet is half the escape speed, calculate the temperature of the atmosphere at a height H above the surface. Assume `(C_(p))/(C_(V)) = gamma` for the atmospheric gas
View SolutionThe Maxwell-Boltzmann distribution of molecular speeds in a sample of an ideal gas can be expressed as
`f=(4)/(sqrt(pi))((m)/(2kT))^(3//2)v^(2)e^(-(mv^(2))/(2kT)).dv`
Where f represent the fraction of total molecules that have speeds between v and v + dv.m, k and T are mass of each molecule, Boltzmann constant and temperature of the gas.
(a) What will be value of `int_(v=0)^(v=oo)fdv ?`
(b) It is given that `int_(0)^(oo) v^(3)e^(-av^(2))dv=(1)/(2a^(2))`
Find the average speed of gas molecules at temperature T.
View SolutionA large cylindrical tower is kept vertical with its ends closed. An ideal gas having molar mass M fills the tower. Assume that temperature is constant throughout, acceleration due to gravity (g) is constant throughout and the pressure at the top of the tower is zero.
(a) Calculate the fraction of total weight of the gas inside the tower that lies above certain height h.
(b) At what height `h_(0)` the quantity of gas above and below is same. How does the value of h0 change with temperature of the gas in the tower?
View SolutionA physics book was found on a newly discovered island in `18^(th)` century. A problem in the book was as follows. “1 pinch of an ideal gas is kept in a container of volume 1.5 volka. When the temperature is 40 tapu, the gas pressure is 25 phatka. When the temperatue is reduced to – 20 tapu the gas pressure becomes 10 phatka. Find the temperature of absolute zero in tapu.
View SolutionA L shaped container has dimensions shown in the fig. It has circular cross section of radius R. It is placed on a smooth horizontal table. The container is divided into two equal sections by a membrane AB. One section contains nitrogen and the other one contains oxygen. Temperature of both sides is same but pressure in the compartment having `N_(2)` is 4 times that in the other compartment. Due to some reason the membrane gets punctured. Find the distance moved by the cylinder if the cylinder is constrained to move in x direction only [with the help of guiding walls `W_(1) " and " W_(2)`]. There is no friction anywhere and mass of the cylinder and membrane is negligible
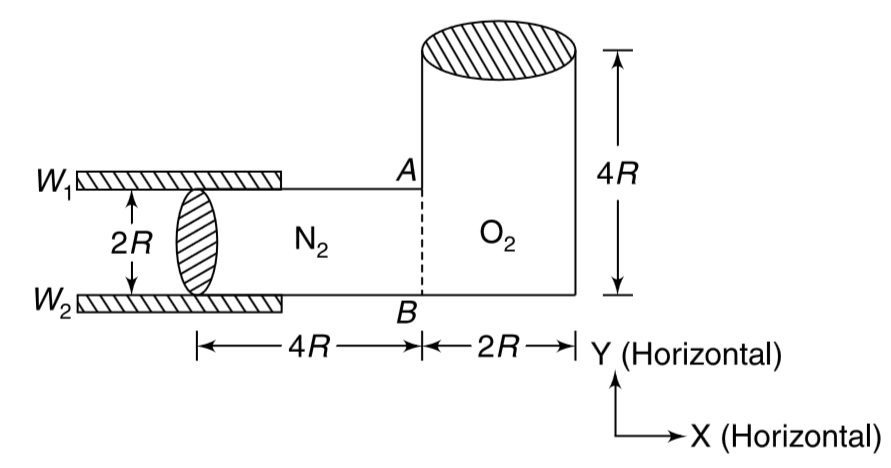
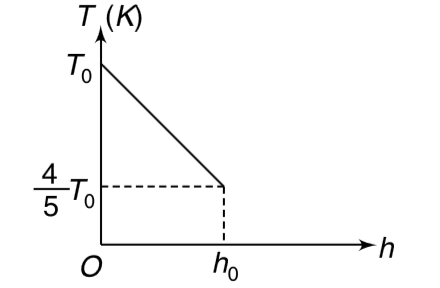
View Solution(a) Assume the atmosphere as an ideal gas in static equilibrium at constant temperature T0. The pressure on the ground surface is P0. The molar mass of the atmosphere is M. Calculate the atmospheric pressure at height h above the ground.
(b) To be more realistic, let as assume that the temperature in the troposphere (lower part of the atmosphere) decreases with height as shown in the figure. Now calculate the atmospheric pressure at a height h0 above the ground.
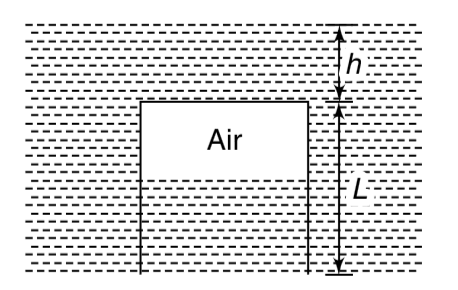
View SolutionA cylindrical container has cross sectional area of `A = 0.05 m^(2)` and length L = 0.775 m. Thickness of the wall of the container as well as mass of the container is negligible. The container is pushed into a water tank with its open end down. It is held in a position where its closed end is h = 5.0 m below the water surface. What force is required to hold the container in this position? Assume temperature of air to remain constant.
Atmospheric pressure `P_(0) = 1 x× 10^(5)` Pa, Acceleration due to gravity `g = 10 m//s^(2)`
Density of water = `10^(3) kg//m^(3)`
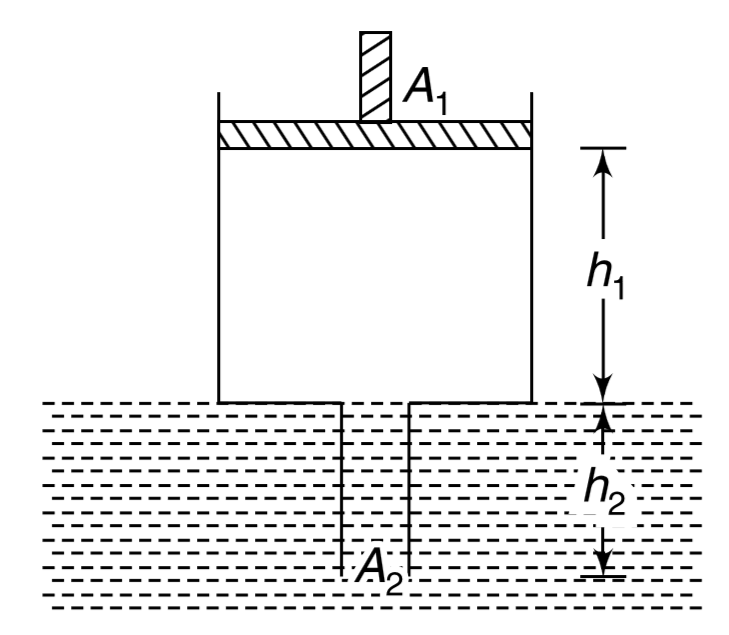
View SolutionA syringe has two cylindrical parts of cross sectional area `A_(1) = 4 cm^(2)` and `A_(2) = 1 cm^(2)`. A mass less piston can slide on the inner wall of the part having cross section `A_(1)`. The end of the part having cross section `A_(2)` is open. Syringe is dipped in a large water tank such that the narrower part remains completely submerged and the wider part is filled with air. The length shown in figure are `h_(1) = 55 cm " and " h_(2) = 100` cm. The piston is pushed down by a distance x such that 25% of the air inside the syringe is expelled out through the open end of the narrower part. Assume that the temperature of air remains constant and calculate x.
Density of water = `10^(3) k gm^(– 3) , g = 10 ms^(– 2)`, Atmospheric pressure = `10^(5) Nm^(–2)`.
View SolutionIf an ideal gas is allowed to undergo free expansion it does not cool. But a real gas cools during free expansion. Why?
View SolutionA container has a gas that consists of positively charged ions. The gas undergoes a free expansion in which there is no heat exchange with surrounding. Does the temperature of the gas increases or decreases? Why?
View SolutionA freely sliding massive piston is supported by a spring inside a vertical cylinder as shown. When all air is pumped out of the container, the piston remains in equilibrium with only a tiny gap between the piston and the bottom surface of the cylinder. An ideal gas at temperature `T_(0)` is slowly injected under the piston so that it rises to height `h_(0)` (see figure). Calculate the height of the piston from the bottom of the container if the temperature of the gas is slowly raised to `4 T_(0)`.
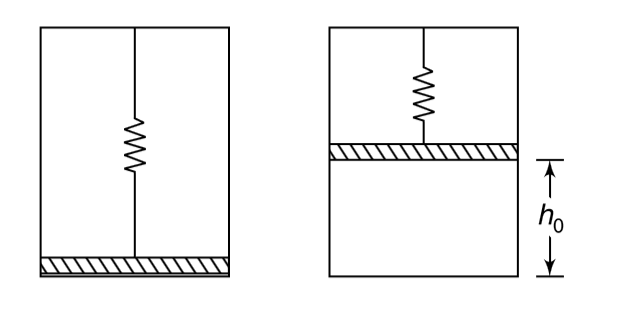
View Solution
Level 2 questions and complete solutions for chapter KINETIC THEORY OF GASES of ARIHANT PHYSICS (HINGLISH) of Class 11