Complete Solutions to Level 1 of chapter KINETIC THEORY OF GASES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINETIC THEORY OF GASES |
| ARIHANT MASTER PROBLEM | Level 1 |
| Number Of Questions | 24 |
| Academic Year | 2023-24 |
An ideal gas at temperature `T_(0)` is contained in a container. By some mechanism, the temperature of the wall AB is suddenly increased to `T (gt T_(0))`. Will the pressure exerted by the gas on wall AB change suddenly? Will it be higher or lower than pressure on wall CD?

View SolutionFind the number of atoms in molecule of a gas for which the ratio of specific heats at constant pressure and constant volume`lamda` becomes `(25)/(21)` times if the rotational degree of freedom of its molecules are frozen. Assume that the gas molecules originally had translational and rotational degree of freedom.
View SolutionAn ideal gas expands following a relation `(P^(2))/(rho)`= constant, where P = pressure and `rho` = density of the gas. The gas is initially at temperature T and density `rho` and finally its density becomes `(rho)/(3)`.
(a) Find the final temperature of the gas. (b) Draw the P – T graph for the process.
View SolutionA container having volume V contains N atoms of a gas X. 2 N atoms of another gas Y is injected into the container and temperature is raised to T and maintained constant. At this temperature the atoms of X and Y combine to form molecule `X_(2)` Y. Find the pressure inside the container after the reaction is completed
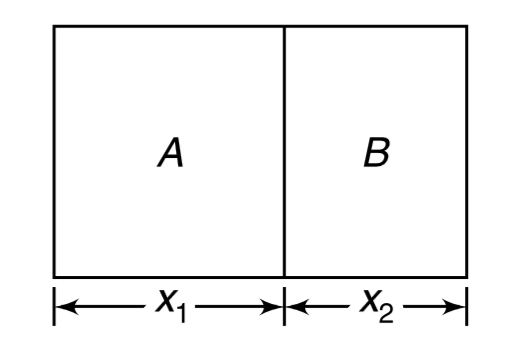
View SolutionA conducting piston separates a cylindrical tube into two compartments A and B. The two compartments contain equal mass of two different gases. The molar mass of two gases are `M_(A) = 32 g " and " M_(B) 28 g`. Find the ratio of lengths `(X_(1) : X_(2))` of the two compartments in equilibrium.
View SolutionA container of volume `V_(1)` has an ideal gas of molar mass `M_(1)` at pressure `P_(1)` and temperature `T_(1)`. Another container of volume `V_(2)` has another ideal gas of molar mass `M_(2)` at pres- sure `P_(2)` and temperature `T_(2)`. Two gases are mixed in a vessel and acquire an equilibrium temperature and pressure of `T_(0)` and `P_(0)` respectively. Find the density of the mixture.
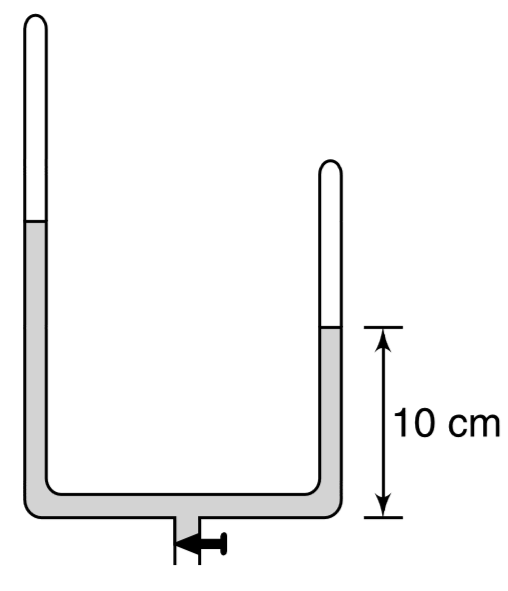
View SolutionA U shaped tube has two arms of equal cross section and lengths `l_(1) = 80` cm and `l_(2) = 40` cm. The open ends are sealed with air in the tube at a pressure of 80 cm of mercury. Some mercury is now introduced in the tube through a stopcock connected at the bottom (the air is not allowed to leak out). In steady condition the length of mercury column in the shorter arm was found to be 10 cm. Find the length of the mercury column in the longer arm. Neglect the volume of the part of the tube connecting two arms and assume that the temperature is constant.
View SolutionTidal volume is that volume of air which is inhaled (and exhaled) in one breath by a human during quiet breathing. For a normal man this volume is close to 0.6 litre. 35% of oxygen (in terms of molecular count) gets converted into carbon – di – oxide in the exhaled air. Nearly 21% of the air that we breath in is oxygen. Assume that a man is breathing when the air is at STP and the moisture content of inhaled and exhaled air is same. Estimate the difference in mass of an inhaled breath and exhaled breath.
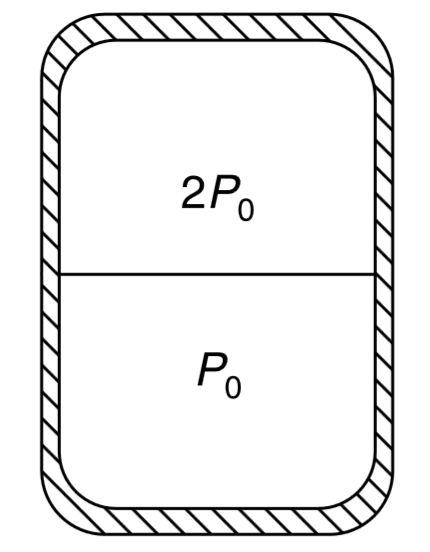
View SolutionA cylindrical container of volume `V_(0)` is divided into two parts by a thin conducting separator of negligible mass. The walls of the container are adiabatic. Ideal gases are filled in the two parts such that the pressures are `P_(0) " and " 2 P_(0)` when the separator is held in the middle of the container (see figure). Now the separator is slowly slid and released in a position where it stays in equilibrium. Find the volume of the two parts.
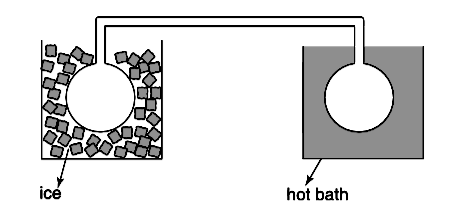
View SolutionTwo identical glass bulbs are interconnected by a thin tube of negligible volume. An ideal gas is filled in the bulbs at STP. One bulb is placed in a tub of melting ice and the other bulb is placed in a hot bath. The gas pressure in the bulbs becomes 1.5 times. Find the tem perature of the hot bath. Which bulb has more gas?
View SolutionTwo states – 1 and 2 – of an ideal gas has been shown in VT graph. In which state is the pressure of the gas higher?
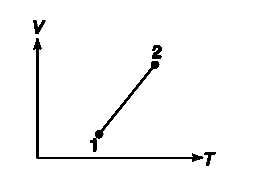
View SolutionA cylindrical tube of cross sectional area A and length L is filled with an ideal gas. Temperature of the gas varies linearly from `T_(0)` at one end to` 2 T_(0)` at the other end. Calculate the number of mole of the gas in the tube assuming pressure to be uniform throughout equal to P.
View SolutionCalculate mean free path length `lamda` for molecules of an ideal gas at STP. It is known that molecular diameter is `2 x× 10^(–10)` m.
View SolutionA jar contains a gas and a few drops of water at absolute temperture `T_(1)`. The pressure in the jar is `830mm` of mercury. The temperature of the jar is reduced by `1%`. The saturation vapour pressures of water at the two temperatures are `30mm` of mercury and `25mm` of mercury. Calculate the new pressure in the jar.
View SolutionA close container of volume `0.02 m^(3)` contains a mixture of neon and another gas A of unknown molecular mass. The container contains 4 g of Neon and 24 g of gas A. At a temperature of `27^(@)C` the pressure of the mixture is `105 N//m^(2)`. Is there any possibility of finding gas A in the atmosphere of a planet of radius 600 km and mean density `r = 5 x× 103 kg//m^(3)` ?
Temperature of the planet is `2200^(@)C`.
Molar molecular mass of neon = 20 g,
Gas constant `R = 8.314 "J mol"^(–1) K^(–1)`
Gravitational constant `G = 6.67 x× 10^(–11) N m^(2) kg^(–2)`
View SolutionWe know that volume (V ) occupied by a substance scales as `x^(3)` , where x is the average distance between its molecules. Assume that water vapour at `100^(@)C` and atmospheric pressure has average intermolecular separation equal to `x_(v)` and for liquid water at `100^(@)C` the intermolecular separation is `x_(w)`. Find the ratio `(X_(v))/(x_(w))` considering density of water at `100^(@)C` to be `1.0 x× 103 kg//m^(3)` and taking water vapour as an ideal gas. Atmospheric pressure `P_(0) = 1.0 x× 10^(5) N//m^(2)` , Gas constant `R = 8.3 "J mol"^(–1) K^(–1)`.
View SolutionThe diameter of molecules of a gas, considered as sphere, is about `3 x× 10^(–10)` m. Assume the entire volume occupied by the gas to be divided into cubic cells with one molecule per cell. Estimate the distance between molecules in terms of molecular diameter under standard conditions.
View SolutionThe core of the sun is a plasma. It is at a temperature of the order of `10^(7)` K and contains equal number of protons and electrons. The density of the core of the Sun is `10^(5) kg m^(–3)` . Assume that molar mass of proton is `1 "g mol"^(–1)` and the mass of an electron to be negligible compared to the mass of a proton. Estimate the pressure at the core of the sun. Assume that plasma behaves like an ideal gas.
View SolutionCalculate the rms speed of He and `N_(2)` molecules in the atmosphere at 300 K. Explain why our atmosphere has only a small amount of helium though it has large nitrogen content. The sun has temperature close to 6000 K. How can you explain the existence of He in the Sun.
View SolutionA cylinder of oxygen, used as medical aid, has a volume of 16 L. It is filled to a pressure of `1.37 x× 10^(7) Nm^(–2)` above the atmospheric pressure at room temperature of 300 K. When in use, the flow rate at atmospheric pressure is `2.4 L//"min"`. How long will the cylinder last? Atmospheric pressure is `10^(5) Nm^(– 2)`.
View SolutionIt is known that pressure of a gas increases if–
(A) You increase the temperature of the gas while holding its volume constant.
(B) You compress the gas holding its temperature constant.
(i) In which of the two cases [A or B] the average impulse imparted by a gas molecule to the container wall during a collision increases?
(ii) In which of the two cases the frequency of collisions of gas molecules with the container wall increases.
View SolutionAn ideal gas undergoes a cyclic process `A to B to C to D` for which P – T graph is as shown. Draw P – V and V – T of graph to represent the same process.
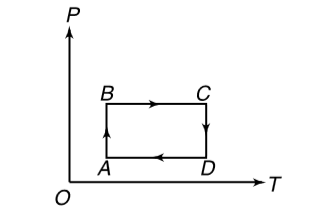
View SolutionAn insulated cylindrical vessel is divided into three identical parts by two partitions 1 and 2. The left part contains `O_(2)` gas, the middle part has `N_(2)` and the third chamber has vacuum. The average molecular speed in oxygen chamber is `V_(0)` and that in nitrogen chamber is `sqrt((8)/(7)) V_(0)`. Pressure of the gases in two chambers is same. Partition 1 is removed and the gases are allowed to mix. Now the stopper holding the partition 2 is removed and it slides to the right wall of the container, so that the mixture of gases occupy the entire volume of the container.
Find the average speed of `O_(2)` molecules now.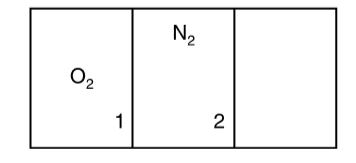
View SolutionIn a cylindrical container two pistons enclose gas in two compartments as shown in the figure. The pistons have negligible thickness and can move without friction. The sys- tem is originally in equilibrium. The outer piston is slowly moved out by 10 cm and the inner piston is found to move by 4 cm. Find the distance of the inner piston in equilibrium from the closed end of the cylinder if the outer piston is slowly moved out of the cylinder. Assume temperature of the gas to remain constant.
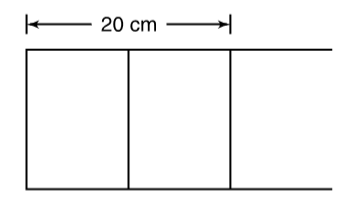
View Solution
Level 1 questions and complete solutions for chapter KINETIC THEORY OF GASES of ARIHANT PHYSICS (HINGLISH) of Class 11