Complete Solutions to Surface tension of chapter SURFACE TENSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SURFACE TENSION |
| ARIHANT MASTER PROBLEM | Surface tension |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
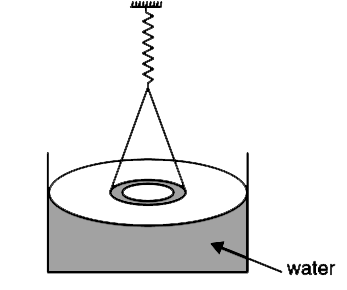
A circular ring has inner and outer radii equal to `10 mm and 30 mm` respectively Mass of the ring is `m = 0.7` g. It gently pulled out vertically from a water surface by a sensitive spring. When the spring is stretched `3.4 cm` from its equilibrium position the ring is on verge of being pulled out from the water surface. If spring constant is `k = 0.7 Nm^(–1)` find the surface tension of water.
View SolutionA long thin walled capillary tube of mass M and radius r is partially immersed in a liquid of surface tension T. The angle of contact for the liquid and the tube wall is `30^(@)`. How much force is needed to hold the tube vertically? Neglect buoyancy force on the tube.
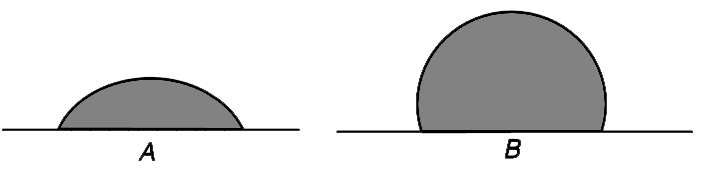
View Solution(i) Water drops on two surfaces A and B has been shown in figure. Which surface is hydrophobic and which surface is hydrophilic?
(ii) A liquid is filled in a spherical container of radius R till a height h. In this position the liquid surface at the edges is also horizontal. What is the contact angle between the liquid and the container wall?

View SolutionA conical pipe shown in figure has a small water drop. In which direction does the drop will tend to move?
View SolutionA narrow tube of length `l` and radius `r` is sealed at one end. Its open end is brought in contact with the surface of water while the tube is held vertical. The water rises to a height `h` in the tube. The contact angle of water with the tube wall is `theta`, density of water is `rho` and the atmospheric pressure is `P_(o)`. Find the surface tension of the liquid. Assume that the temperature of air inside the tube remains constant and the volume of the meniscus is negligible.
View SolutionThe internal radius of one arm of a glass capillary `U` tube is `r_(1)` and for the second arm it is `r_(2)(gt r_(1))`. The tube is filled with some mercury having surface tension `T` and contact angle with glass equal to `90^(@) + theta`.
(a) It is proposed to connect one arm of the `U` tube to a vacuum pump- so that the mercury level in both arms can be equalized. To which arm the pump shall be connected?
(b) When mercury level in both arms is same, how much below the atmospheric pressure is the pressure of air in the arm connected to the pump?
View SolutionIn a horizontal capillary tube, the rate of capillary flow depends on the surface tension force as well as the viscous force. Lueas and washburn showed that the length `(x)` of liquid penetration in a horizontal capillary depends on a factor `(k)` apart from time (t). The factor is given by `k = [(rTcos theta)/(2ne)]^(1//2)` , where r, T, `theta` and `ne` are radius of the capillary tube, surface tension, contact angle and coefficient of viscosity respectively. If the length of liquid in the capillary grows from zero to `x_(0)` in time `t_(0), how much time will be needed for the length to increases from `x_(0) to 4x_(0)`.
View SolutionA glass tube of radius R is covered with a liquid film at its one end. Air is blown slowly into the tube to gradually increase the pressure inside. What is the maximum pressure that the air inside the tube can have? Assume that the liquid film does not leave the surface (whatever its size) and it does not get punctured. Surface tension of the liquid is T and atmospheric pressure is `P_(o)`.

View SolutionWhy bubbles can be formed using soap water but we do not have bubbles formed out of pure water?
View SolutionA tapering glass capillary tube A of length `0.1 m` has diameters `10^(-3)` m and `5 × 10^(4)` m at the ends. When it is just immersed in a liquid at `0^(@)`C with larger radius in contact with liquid surface, the liquid rises `8 × 10^(-2)` m in the tube. In another experiment, in a cylindrical glass capillary tube B, when immersed in the same liquid at `0^(@)`C, the liquid rises to `6 × 10^(-2)` m height. The rise of liquid in tube B is only `5.5 × 10^(-2)` m when the liquid is at `50^(@)`C. Find the rate at which the surface tension changes with temperature considering the change to be linear. The density of liquid is `(1//14) × 10^(4) kg//m^(3)` and the angle of contact is zero. Effect of temperature on the density of liquid and glass is negligible.
View Solution(i) One end of a uniform glass capillary tube of radius `r = 0.025` cm is immersed vertically in water to a depth `h = 1cm`. Contact angle is `0^(@)`, surface tension of water is `7.5 × 10–2 N//m`, density of water is `rho = 10^(3) kg//m^(3)` and atmospheric pressure is `P_(o) = 10^(5) N // m^(2)`
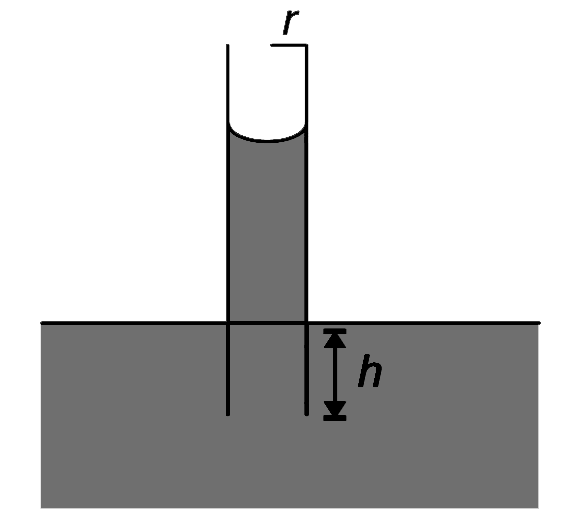
Find the excess pressure to be applied on the water in the capillary tube so that -
(a) The water level in the tube becomes same as that in the vessel.
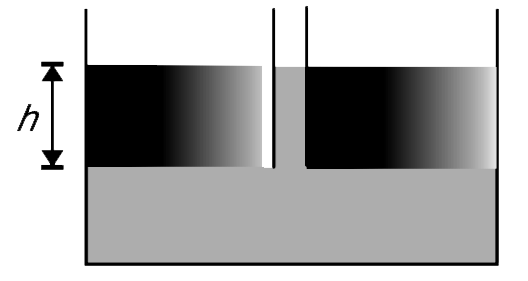
(b) Is it possible to blow out an air bubble out of the tube by increasing the pressure? (ii) A container contains two immiscible liquids of density `rho_(1)` and `rho_(2) (rho_(2) gt rho_(1))`. A capillary of radius r is inserted in the liquid so that its bottom reaches up to denser liquid and lighter liquid does not enter into the capillary. Denser liquid rises in capillary and attain height equal to h which is also equal to column length of lighter liquid. Assuming zero contact angle find surface tension of the heavier liquid.
View SolutionThe radii of two columns in a `U` tube are `r_(1) and r_(2) (r_(1) gt r_(2))`. A liquid of density `rho` is filled in it. The contact angle of the liquid with the tube wall is `theta`. If the surface tension of the liquid is T then plot the graph of the level difference (h) of the liquid in the two arms versus contact angle `theta`. Plot the graph for angle `theta` changing from `0^(@) to 90^(@)`. Assume the curved surface of meniscus to be part of a sphere.

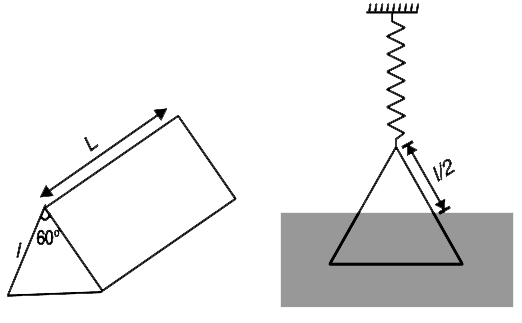
View SolutionA glass prism has its principal section in form of an equilateral triangle of side length `l`. The length of the prism is L (see fig.). The prism, with its base horizontal, is supported by a vertical spring of force constant k. Half the slant surface of the prism is submerged in water. Surface tension of water is T and contact angle between water and glass is `0^(@)`. Density of glass is d and that of water is `rho ( lt d)`. Calculate the extension in the spring in this position of equilibrium.
View SolutionTwo capillaries of small cross section are connected as shown in the figure. The right tube has cross sectional radius `R` and left one has a radius of `r (lt R)`. The tube of radius `R` is very long where as the tube of radius r is of short length. Water is slowly poured in the right tube. Contact angle for the tube wall and water is `theta = 0^(@)`. Let h be the height difference between water surface in the right and left tube. Surface tension of water is `T` and its density is `rho`.
(a) Find the value of h if the water surface in the left tube is found to be flat.
(b) Find the maximum value of h for which water will not flow out of the left tube .
View SolutionA soap bubble of radius `r` is formed inside another soap bubble of radius `R (gt r)`. The atmospheric pressure is `P_(0)` and surface tension of the soap solution is T. Calculate change in radius of the smaller bubble if the outer bubble bursts. Assume that the excess pressure inside a bubble is small compared to `P_(0)`.
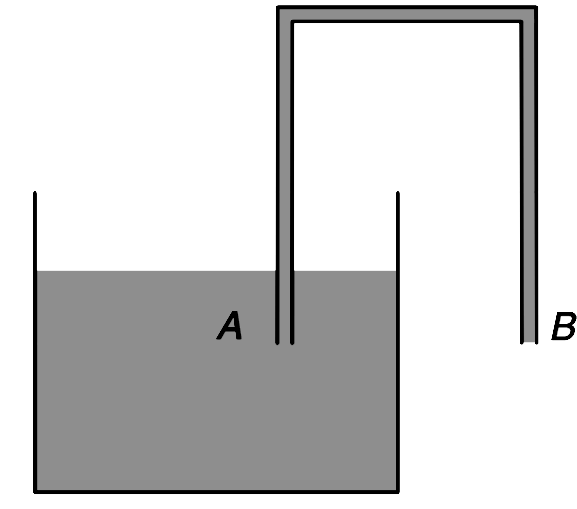
View SolutionIn the siphon shown in the figure the ends `A` and `B` of the tube are at same horizontal level. Water fills the entire tube but it does not flow out of the end B. With the help of a diagram show how the water surface at end B changes if the end B were slightly lower than the position shown.
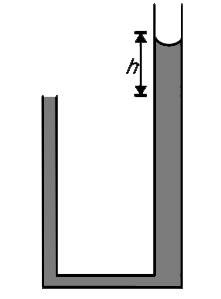
View SolutionA glass capillary tube sealed at the upper end has internal radius `r`. The tube is held vertical with its lower end touching the surface of water. Calculate the length `(L)` of such a tube for water in it to rise to a height `h (lt L)`. Atmospheric pressure is `P_(o)` and surface tension of water is T. Assume that water perfectly wets glass (Density of water = `rho`)
View SolutionIn the last question let the length of the tube be L and its outer radius be R. Water rises in it to a height h. Calculate the vertical force needed to hold the tube in this position. Mass of empty tube is M.
View SolutionA glass capillary tube is held vertical and put into contact with the surface of water in a tank. It was observed that the liquid rises to the top of the tube before settling to an equilibrium height `h_(0)` in the tube. Assume that water perfectly wets glass and viscosity is small. Is the length of the capillary tube larger then `2h_(0)`?
View SolutionTwo soap bubbles of radii `r_(1) and r_(2)` are attached as shown. Find the radius of curvature of the common film ACB.
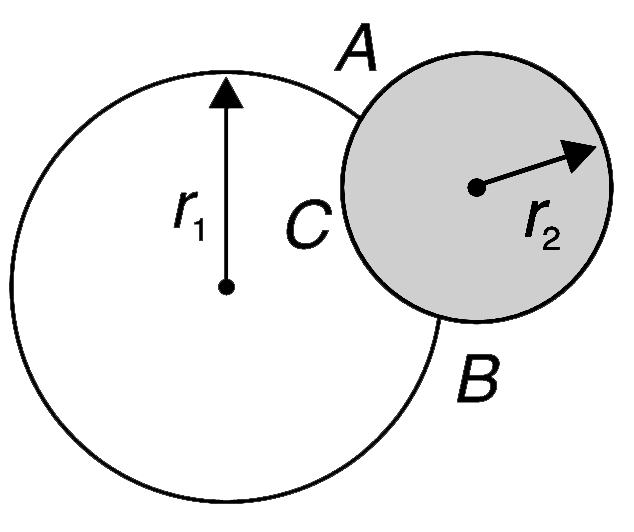
View Solution(a) In the last question find the angle between the tangents drawn to the bubble surfaces at point A.
(b) In the above question assume that `r_(1) = r_(2) = r`. What is the shape of the common interface ACB? Find length AB in this case.
(c) With `r_(1) = r_(2) = r` the common wall bursts and the two bubbles form a single bubble find the radius of this new bubble. It is given that volume of a truncated sphere of radius R and height y is `pi/3 y ^(2) (3R -y)` [see figure]

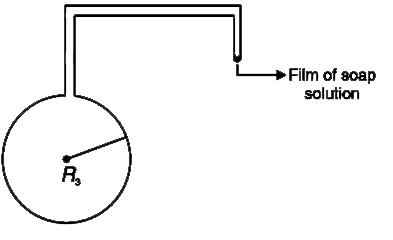
View SolutionTwo soap bubbles of radius `R_(1) and R_(2) (lt R_(1))` are joined by a straw. Air flows from one bubble to another and a single bubble of radius `R_(3)` remains.
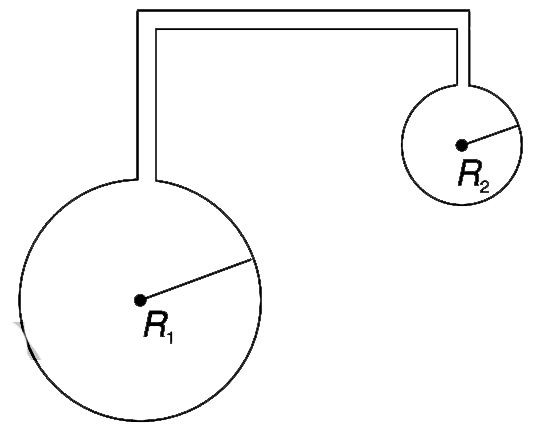
(a) From which bubble does the air flow out ?
(b) Assuming no temperature change and atmospheric pressure to be `P_(o), find the surface tension of the soap solution.
View SolutionIn the last problem, one of the bubbles supplies its entire air to the other bubble and a film of soap solution is formed at the end of the straw which keeps it closed. What is the radius of curvature of this film if the bigger bubble has grown in size and its radius has become `R_(3)`.
View SolutionConsider a rain drop falling at terminal speed. For what radius `(R)` of the drop can we disregard the influence of gravity on its shape? Surface tension and density of water are `T` and `rho` respectively.
View SolutionA soap bubble has radius R and thickness of its wall is a. Calculate the apparent weight `(= true weight - Buoyancy)` of the bubble if surface tension of soap solution and its density are T and d respectively. The atmospheric pressure is `P_(0)` and density of atmospheric air is `rho_(0)`. By assuming `a = 10^(–6) m, R = 10 cm, P_(0) = 10^(5) Nm^(–2), rho_(0) = 1.2 kg m^(–3), d = 10^(3) kg m^(–3), T = 0.04 Nm^(–1)`, show that the weight of the bubble is mainly because of water in the skin. What is weight of the bubble?
View SolutionA soap bubble is blown at the end of a capillary tube of radius a and length L. When the other end is left open, the bubble begins to deflate. Write the radius of the bubble as a function of time if the initial radius of the bubble was `R_(0)`. Surface tension of soap solution is T. It is known that volume flow rate through a tube of radius a and length L is given by Poiseuille’s equation- `Q=(pia^(4)DeltaP)/(8ne L)`

Where `DeltaP` is pressure difference at the two ends of the tube and `ne` is coefficient of viscosity. Assume that the bubble remains spherical.
View SolutionTwo blocks are floating in water. When they are brought sufficiently close they are attracted to each other due to surface tension effects. When the experiment is repeated after replacing water with mercury, once again the two blocks are attracted. Explain the phenomena. It is given that water wets the material of the block where as mercury does not.
View SolutionA long thin string has a coat of water on it. The radius of the water cylinder is r. After some time it was found that the string had a series of equally spaced identical water drops on it. Find the minimum distance between two successive drops.
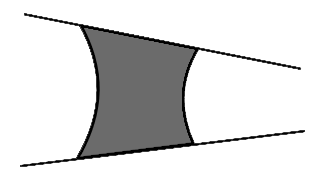
View SolutionA liquid having surface tension `T` and density `rho` is in contact with a vertical solid wall. The liquid surface gets curved as shown in the figure. At the bottom the liquid surface is flat. The atmospheric pressure is `P_(o)`.
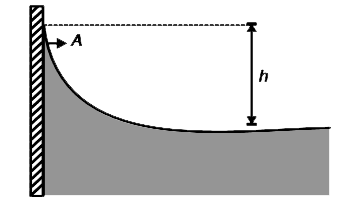
(i) Find the pressure in the liquid at the top of the meniscus (i.e. at A)
(ii) Calculate the difference in height `(h)` between the bottom and top of the meniscus.
View SolutionIs it possible that water evaporates from a spherical drop of water just by means of surface energy supplying the necessary latent heat of vaporisation? The drop does not use its internal thermal energy and does not receive any heat from outside. It is known that water drops of size less than `10^(–6)` m do not exist. Latent heat of vaporisation of water is `L = 2.3 × 10^(6) Jkg^(–1)` and surface tension is `T = 0.07 Nm^(–1)`.
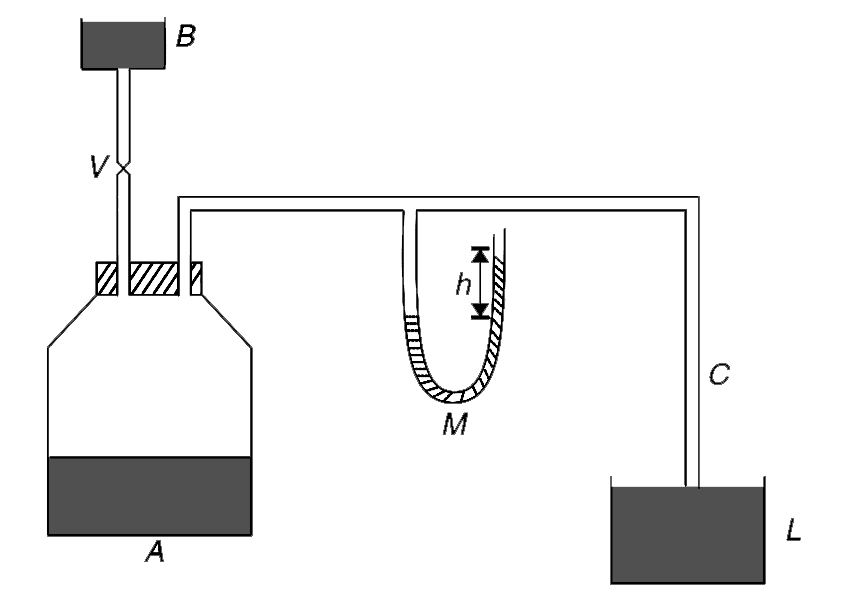
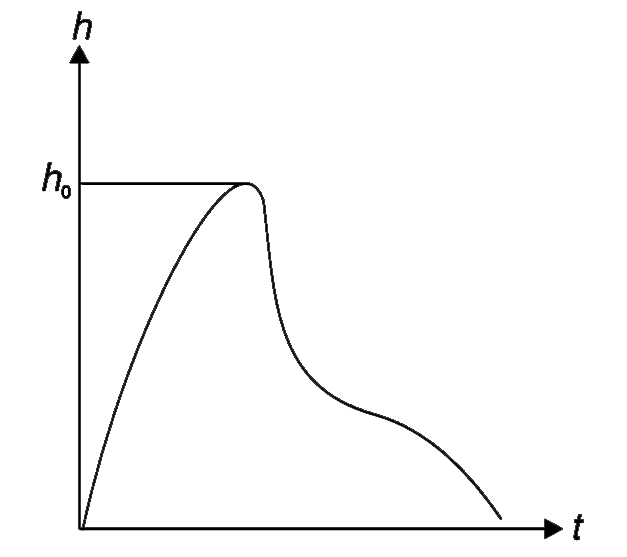
View SolutionIn the arrangement shown in the figure, `A` is a jar half filled with water and half filled with air. It is fitted with a leak proof cork. `A` tube connects it to a water vessel `B`. Another narrow tube fitted to `A` connects it to a narrow tube `C` via a water monometer M. The tip of the tube `C` is just touching the surface of a liquid `L`. Valve `V` is opened at time `t = 0` and water from vessel `B` pours down slowly and uniformly into the jar `A`. An air bubble develops at the tip of tube `C`. The cross sectional radius of tube `C` is r and density of water is `rho`. The difference in height of water `(h)` in the two arms of the manometer varies with time 't' as shown in the graph. Find the surface tension of the liquid `L`.
View SolutionA curved liquid surface has radius of curvature `R_(1) and R_(2)` in two perpendicular directions as shown in figure. Surface tension of the liquid is `T`. Find the difference in pressure on the concave side and the convex side of the liquid surface.
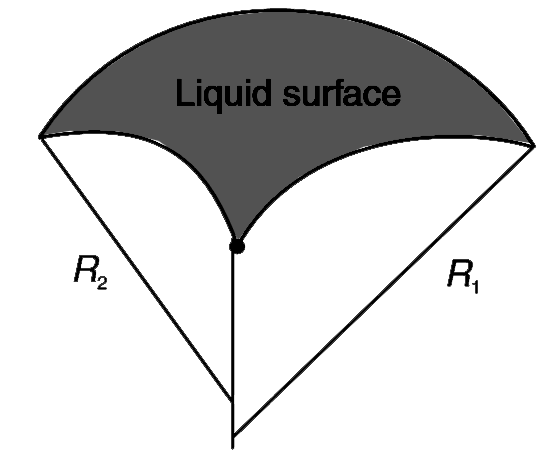
View SolutionA capillary tube of radius `r` and height `h_(1)` is connected to a broad tube of large height as shown in the figure. Water is poured into the broad tube – drop by drop. Drops fall at regular intervals. Plot the variation of height of water in both tubes with time. Initially the tube and capillary are empty. Neglect the volume of the connecting pipe.

View Solution
Surface tension questions and complete solutions for chapter SURFACE TENSION of ARIHANT PHYSICS (HINGLISH) of Class 11