Complete Solutions to Level 3 of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| ARIHANT MASTER PROBLEM | Level 3 |
| Number Of Questions | 9 |
| Academic Year | 2023-24 |
Two particles of mass `m_(1) " and " m_(2)` are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity `V_(0)` along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass `m_(1) (or m_(2))` will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of `m_(1) " and " m_(2)` as a function of time. lt( c) Write the X co ordinates of `m_(1) " and " m_(2)` as a function of time

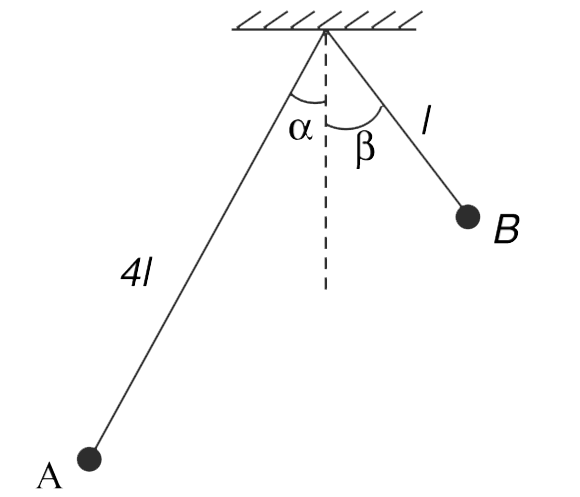
View SolutionTwo simple pendulums A and B have length 4l and l respectively. They are released from rest from the position shown. Both the angles `alpha " and " beta` are small. Calculate the time after which the two string become parallel for the first time if-
(a) `alpha=beta` " " (b)`beta=1.5 alpha`
View SolutionA simple pendulum has a bob of mass m and it is oscillating with a small angular ampitude of `theta_(0)`. Calculate the average tension in the string averaged over one time period. [For small `theta` take `cos theta =1-(theta^(2))/(2)]`
View SolutionAssume a smooth hole drilled along the diameter of the earth. If a stone is dropped at one end it reaches the other end of the hole after a Time `T_(0)`. Now instead of dropping the stone, you throw it into the hole with an initial velocity u. How big should u be, so that the stone appears at the other end of the hole after a time `(T_(0))/(2)`. Express your answer in terms of acceleration due to gravity on the surface of the earth (g) and the radius of the earth (R ).
View SolutionA large horizontal turntable is rotating with constant angular speed `omega` in counterclockwise sense. A person standing at the centre, begins to walk eastward with a constant speed V relative to the table. Taking origin at the centre and X direction to be eastward calculate the maximum X co-ordinate of the person.
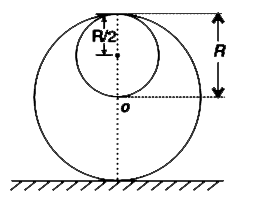
View SolutionA spherical cavity of radius`(R )/(2)` is removed from a solid sphere of radius R as shown in fig. The sphere is placed on a rough horizontal surface as shown. The sphere is given a gentle push. Friction is large enough to prevent slippage. Prove that the sphere perform SHM and find the time period.
View SolutionTwo blocks 1 and 2, each having mass m, are placed on a smooth table connected to three identical springs as shown in the figure. Each spring has a force constant K. Initially, all springs are relaxed. The system is disturbed and starts moving. Let `x_(1) " and " x_(2)` represent the displacements of the two blocks from their respective mean positions.
(a) Prove that the quantity `A = x_(1) + x_(2)` varies sinusoidally and calculate its angular frequency wa.
(b) Prove that the quantity `B = x_(1) - x_(2)` varies sinusoidally and calculate its angular frequency wb.
(c) Prove that motion of block 1 is superposition of two SHMs. Write frequency of the component SHMs.

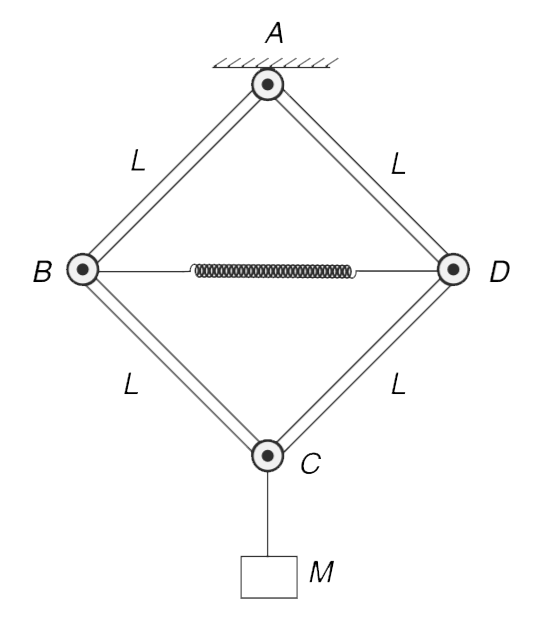
View SolutionFour identical mass less rods are connected by hinged joints to form a rhombus of side length L. Rods can rotate freely about the joints. The joints B and D are connected by a mass less spring of relaxed length 1.5 L. The system is suspended vertically with a load of mass M attached at C (see fig). In equilibrium the rods form an angle of `30^(@)` with the vertical. Find time period of small oscillations of the load.
View SolutionTwo identical blocks 1 and 2, each of mass m, are kept on a smooth horizontal surface, connected to three springs as shown in the figure. Each spring has a force constant k. Under suitable initial conditions, the two blocks oscillate in phase and their respective displacement from the mean position is given by
`x_(1)=A sin omega t " and " x_(2)=A sin omega t`
(i) Suggest one such initial condition that will result in such oscillation.
(ii) Find `omega`

View Solution
Level 3 questions and complete solutions for chapter SIMPLE HARMONIC MOTION of ARIHANT PHYSICS (HINGLISH) of Class 11