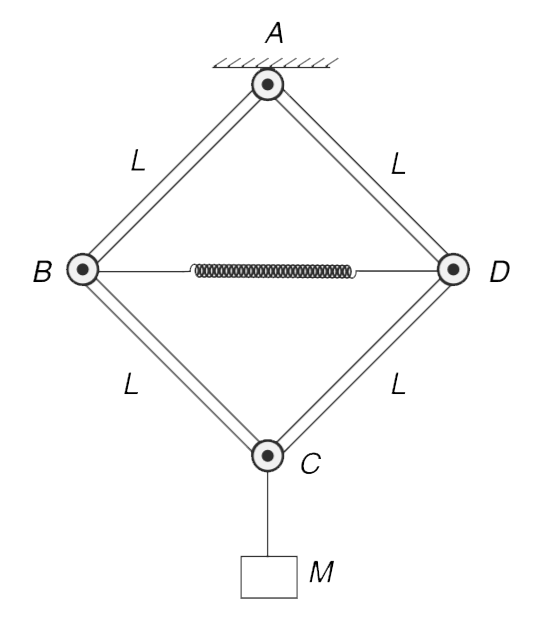
Four identical mass less rods are connected by hinged joints to form a rhombus of side length L. Rods can rotate freely about the joints. The joints B and D are connected by a mass less spring of relaxed length 1.5 L. The system is suspended vertically with a load of mass M attached at C (see fig). In equilibrium the rods form an angle of 30∘ with the vertical. Find time period of small oscillations of the load.
The correct Answer is:T=2π√L2√3g
Topper's Solved these Questions
Similar Questions
Four weightless rods of length l each are connected by hinged joints and form a rhomb (Fig). A hinge A is fixed, and a load is suspended to a hinge C. Hinges D and B are connected by a weightless spring of length 1.5l in the undeformed state. In equilibrium, the rods form angles α0=30∘ with the vertical. Determine the period T of small oscillations of the load.

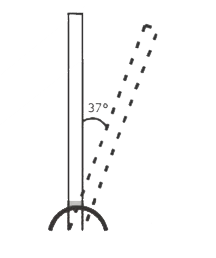
View SolutionA uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
View Solution
Knowledge Check
A rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
 Amg/2B2mgCmg/2√3D√3mg
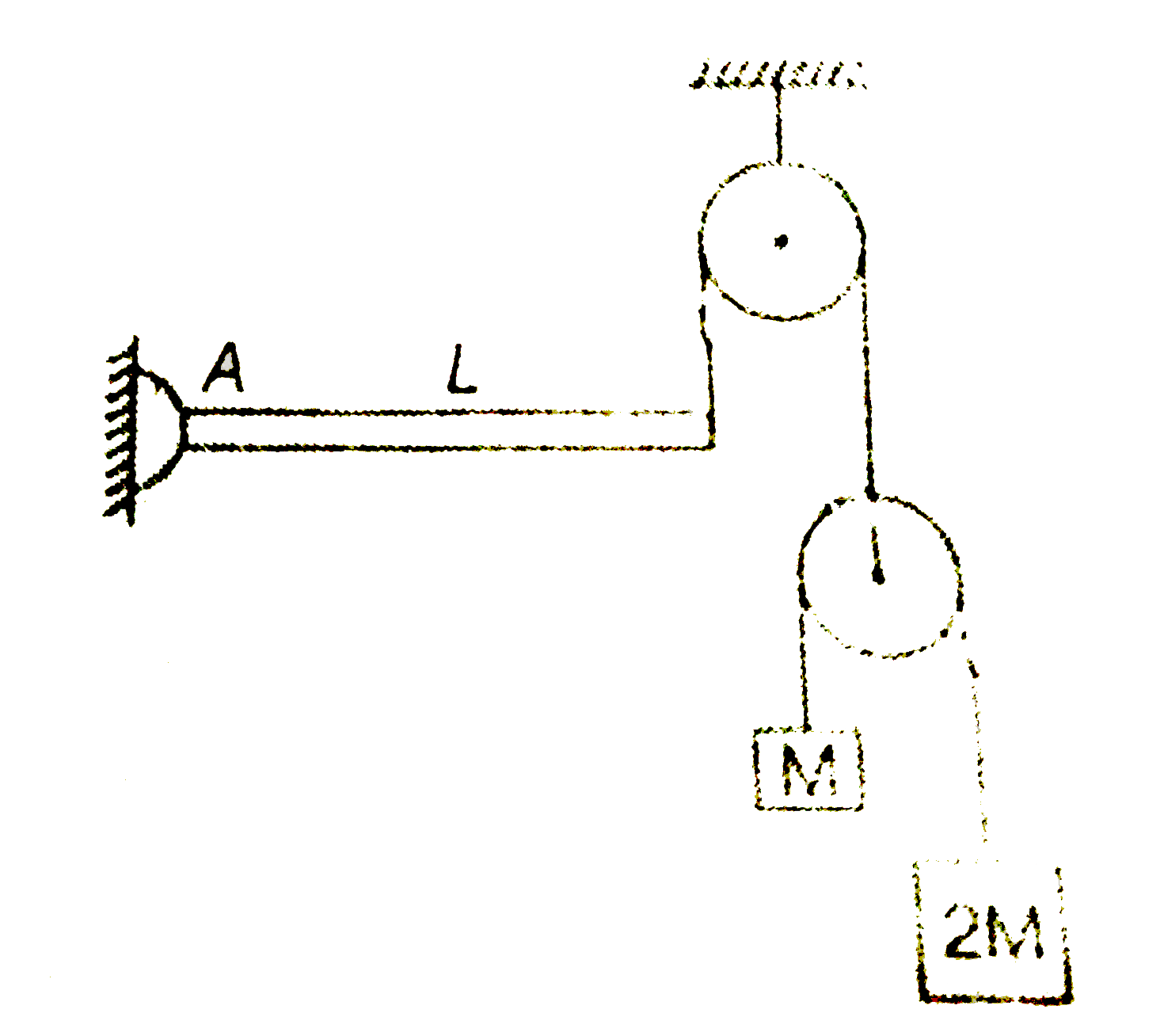
Amg/2B2mgCmg/2√3D√3mgConsider the situation shown in the figure. Uniform rod of length L can rotat freely about the hinge A in vertical plane. Pulleys and stringa are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of the rod is
 A43MB83MC163MD323M
A43MB83MC163MD323MA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
 Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
A rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:

View SolutionConsider the situation shown in the figure. Uniform rod of length L can rotat freely about the hinge A in vertical plane. Pulleys and stringa are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of the rod is

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionTwo identical uniform rods AB and CD, each of length L are jointed to form a T-shaped frame as shown in figure. Locate the centre of mass of the frame. The centre of mass of a uniform rod is at the middle point of the rod.

View SolutionA conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View Solution
