Complete Solutions to Level 2 of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| ARIHANT MASTER PROBLEM | Level 2 |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
Two particles A and B are describing SHM of same amplitude (a) and same frequency (f) along a common straight line. The mean positions of the two SHMs are also same but the particles have a constant phase difference between them. It is observed that during the course of motion the separation between A and B is always less than or equal to a.
(a) Find the phase difference between the particles.
(b) If distance between the two particles is plotted with time, with what frequency will the graph oscillate?
View Solution(i) A particle of mass m executes SHM in xy- plane along a straight line AB. The points A (a, a) and B (- a, - a) are the two extreme positions of the particle. The particle takes time T to move from one extreme A to the other extreme B. Find the x component of the force acting on the particle as a function of time if at t = 0 the particle is at A. (ii) Two particle A and B are performing SHM along X-axis and Y-axis respectively with equal amplitude and frequency of 2 cm and 1 Hz respectively. Equilibrium positions for the particles A and B are at the coordinate (3, 0) and (0, 4) respectively. At t = 0, B is at its equilibrium position and moving toward the origin, while A is nearest to the origin. Find the maximum and minimum distances between A and B during their course of motion
View SolutionA particle is performing SHM along x - axis and equation for its motion is `x = a cos (pit)`
Let the time t be expressed as `(t)/(2) =n+m`
Where n = 0,1,2,3,4.... and m is a positive fraction.
Calculate the distance travelled by the particle during the interval from t=0 to t=t if
(a) `m gt 0.5` (b) `m gt 0.5`
View SolutionTwo blocks A and B having mass m = 1 kg and M = 4 kg respectively are attached to a spring and placed vertically on a weighing machine as shown in the figure. Block A is held so that the spring is relaxed. A is released from this position and it performs simple harmonic motion with angular frequency `w = 25 rad s^(-1)`. The spring remains vertical
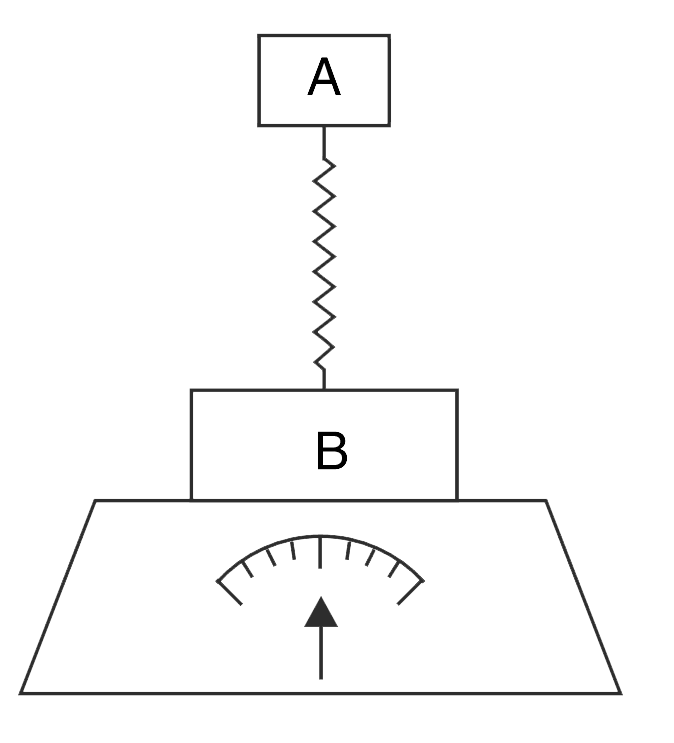
(a) Find the reading of the weighing machine as a function of time. Take t = 0 when A is released.
(b) What is the maximum reading of the weighing machine ?
View SolutionA block of mass M rests on a smooth horizontal table. There is a small gap in the table under the block through which a pendulum has been attached to the block. The bob of the simple pendulum has mass m and length of the pendulum is L. The pendulum is set into small oscillations in the vertical plane of the figure. Calculate its time period. The table does not interfere with the motion of the string.
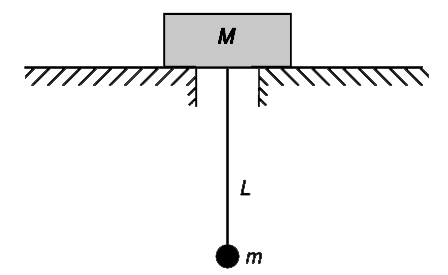
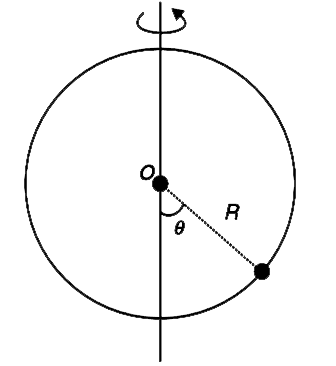
View SolutionA circular wire frame of radius R is rotating about its fixed vertical diameter. A bead on the wire remains at rest relative to the wire at a position in which the radius makes an angle `theta` with the vertical (see figure). There is no friction between the bead and the wire frame. Prove that the bead will perform SHM (in the reference frame of the wire) if it is displaced a little from its equilibrium position. Calculate the time period of oscillation.
View SolutionIn the system shown in the figure the string, springs and pulley are light. The force constant of the two springs are `k_(1) = k " and " k_(2) = 2k`. Block of mass M is pulled vertically down from its equilibrium position and released. Calculate the angular frequency of oscillation. The top surface of the block (represented by line AB) always remains horizontal.

View Solution(i) In the system shown in figure, find the time period of vertical oscillations of the block A. Both the blocks A and B have equal mass of m and the force constant of the ideal spring is k. Pulley and threads are massless
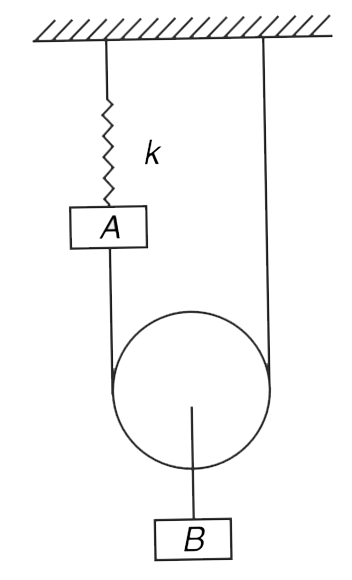
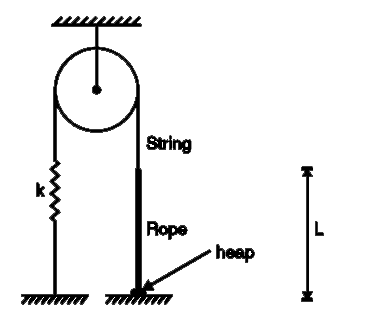
(ii) In the arrangement shown in the figure the spring, string and the pulley are mass less. The force constant of the spring is k. A rope of mass per unit length equal to `lamda (kg m^(-1))` hangs from the string as shown. In equilibrium a length L of the rope is in air and its bottom part lies in a heap on the floor. The rope is very thin and size of the heap is negligible though the heap contains a fairly long length of the rope. The rope is raised by a very small distance and released. Show that motion will be simple harmonic and calculate the time period. Assume that the hanging part of the rope does not experience any force from the heap or the floor (For example there is no impact force while the rope hits the floor while moving downward and there is no impulsive pull when the vertical part jerks a small element of heap into motion).
View SolutionA box B of mass M hangs from an ideal spring of force constant k. A small particle, also of mass M, is stuck to the ceiling of the box and the system is in equilibrium. The particle gets detached from the ceiling and falls to strike the floor of the box. It takes time t for the particle to hit the floor after it gets detached from the ceiling. The particle, on hitting the floor, sticks to it and the system thereafter oscillates with a time period T. Find the height H of the box if it is given that `t=(T)/(6sqrt(2))`. Assume that the floor and ceiling of the box always remian horizontal.

View SolutionA block has a L shaped stand fixed to it. Mass of the block with the stand is M. At the free end of the stand there is a spring which carries a ball of mass m. With the spring in its natural length, the ball is released. It begins to oscillate and the stand is tall enough so that the ball does not hit the block.
(a) Find maximum value of mass (m) of the ball for which the block will not lose contact with the ground?
(b) If the stand is not tall enough and the ball makes elastic impact with the block, will your answer to part (a) change?

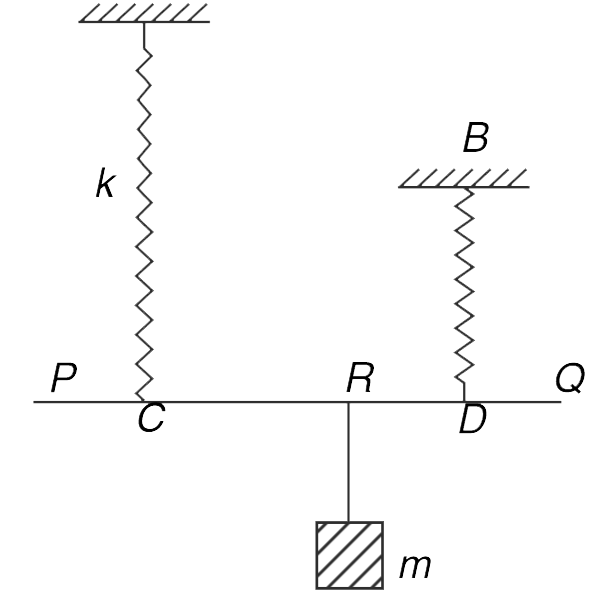
View SolutionTwo ideal springs of same make (the springs differ in their lengths only) have been suspended from points A and B such that their free ends C and D are at same horizontal level. A massless rod PQ is attached to the ends of the springs. A block of mass m is attached to the rod at point R. The rod remains horizontal in equilibrium. Now the block is pulled down and released. It performs vertical oscillations with time period `T =2 pi sqrt((m)/(3k))` where k is the force constant of the longer spring.
(a) Find the ratio of length RC and RD.
(b) Find the difference in heights of point A and B if it is given that natural length of spring BD is L.
View SolutionA block of mass M connected to an ideal spring of force constant k lies in equilibrium on the smooth floor of a room. The other end of the spring is fixed to the left wall of the room. The room begins to move to the right with a constant acceleration `a_(0)`. In the reference frame of the room the block begins to perform simple harmonic motion.
At a certain instant (say `t = t_(0))` when the block was at its left extreme, the acceleration of the room vanishes. Plot the x - t graph for the block taking time t = 0 when the room started accelerating.
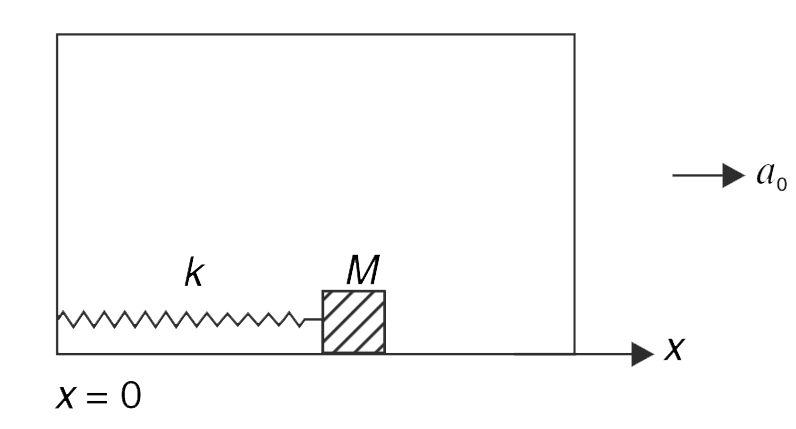
Show the graph till time `t_(0)` and beyond that. Take origin to be at the left wall and positive x direction towards right (as shown in figure). Assume no collision of the block with walls.
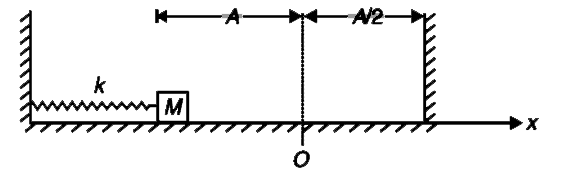
View SolutionA block of mass M connected to an ideal spring of force constant k, is placed on a smooth surface. The block is pushed to the left so as to compress the spring by a length A and then it is released. The block hits an elastic wall at a distance `(3A)/(2)` from its point of release. Assume the collision to be instantaneous.
(a) Calculate the time required by the block to complete one oscillation
(b) Draw the velocity - time graph for one oscillation of the block.
(c) Find the value of k for which average force experienced by the wall due to repeated hitting of the block is `F_(0)`.
View SolutionA particle of mass m is constrained to move along a straight line. A and B are two fixed points on the line at a separation of L. When the particle is at some point P, between A and B, it is acted upon by two forces
`vecF_(1)=((6mg)/(L))vecPA " and " vecF_(2)=((3mg)/(L))vecPB`
At time t=0, the particle is projected from A toward B with a speed of `sqrt(gL)`.
At what time 't' will the particle reach at B for the first time ?

View SolutionAn equilateral prism of mass m is kept on a smooth table between two identical springs each having a force constant of k. The two springs have their lengths perpendicular to the inclined faces of the prism and are constrained to remain straight. The ends of the springs have light pads aligned parallel to the faces of the prism, and distance between pads and the incline faces is d. The prism is imparted a velocity v to the right. Find time period of its oscillation.
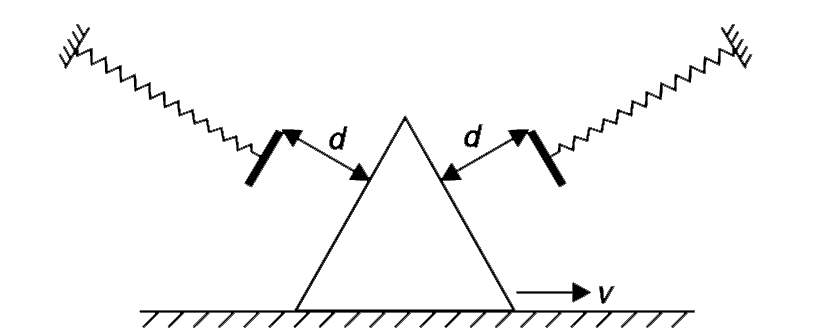
View SolutionTwo blocks rest on a smooth horizontal surface. They are connected by a spring of force constant k. If the system is set into oscillation find its time period.

View SolutionTwo blocks A (2 kg) and B (3 kg) rest on a smooth horizontal surface, connected by a spring of stiffness k = 120 N/m. Initially, the spring is relaxed. At t = 0, A is imparted a velocity u = 2 m/s towards right. Find displacement of block A as a function of time.

View SolutionA spring has force constant `k = 200 N//m` and its one end is fixed. There is a block of mass 2 kg attached to its other end and the system lies on a smooth horizontal table. The block is pulled so that the extension in the spring becomes 0.05 m. At this position the block is projected with a speed of `1 m//s` in the direction of increasing extension of the spring. Consider time t = 0 at the moment the block is projected and find
(a) the extension (or compression) in the spring as a function of time.
(b) the maximum extension in the spring and the time at which it occurs for the first time.
(c) the time after which the speed of the block becomes maximum for the first time. Given: `sin^(-1) (0.446) = 0.46` radian
View SolutionTwo identical simple pendulums A and B are fixed at same point. They are displaced by very small angles `alpha " and " beta ( = 2 alpha)` respectively and are simultaneously released from rest at time t = 0. Collisions between the pendulum bobs are elastic and length of each pendulum is l.
(a) What is the minimum number of collisions between the bobs after which the pendulum B will again reach its original position from where it was released ?
(b) Find the time (t) at which B reaches its initial position for the first time after the release.
(c) Write the kinetic energy of pendulum B just after `n^(th)` collision? Take mass of each bob to be m.
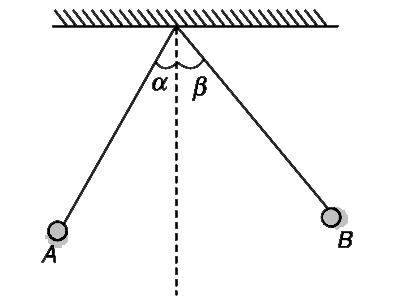
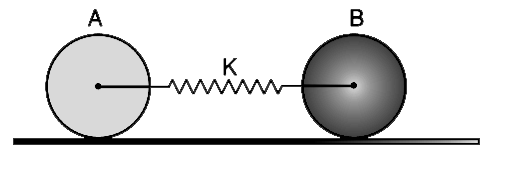
View SolutionTwo spheres A and B of the same mass m and the same radius are placed on a rough horizontal surface. A is a uniform hollow sphere and B is uniform solid sphere. They are tied centrally to a light spring of spring constant k as shown in figure. A and B are released when the extension in the spring is `x_(0)`. Friction is sufficient and the spheres do not slip on the surface. Find the frequency and amplitude of SHM of the sphere A.
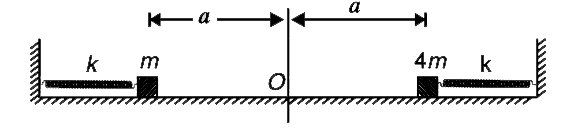
View SolutionTwo small blocks of mass m and 4m are connected to two springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that both the springs get compressed by a distance a. First the block of mass m is released and after it travels through a distance`(1-(sqrt(3))/(2))`
the second block is also released.
(a) At what distance from point O will the two blocks collide?
(b) How much time the two blocks need to collide after the block of mass 4m is released?
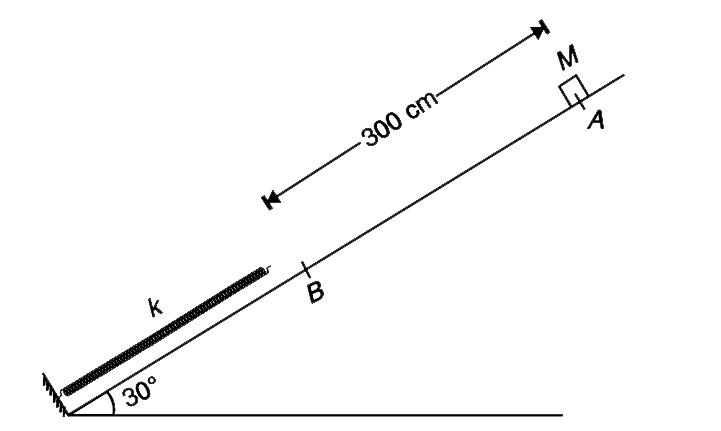
View SolutionA block of mass M = 40 kg is released on a smooth incline from point A. After travelling through a length of 30 cm it strikes an ideal spring of force constant `K = 1000 N//m` . It compresses the spring and then gets pushed back. How much time after its release, the block will be back to point A?
View SolutionTwo tunnels - `T_(1) " and " T_(2)` are dug across the earth as shown in figure. One end of the two tunnels have a common meeting point on the surface of the earth. Two particles `P_(1) " and " P_(2)` are oscillating from one end to the other end of the tunnels. At some instant particles are at mid point of their tunnels as shown in figure. Then -

(a) Write phase difference between the particle `P_(1) " and " P_(2)`. Can the two particles ever meet?
(b) Write the ratio of maximum velocity of particle `P_(1) " and " P_(2)`.
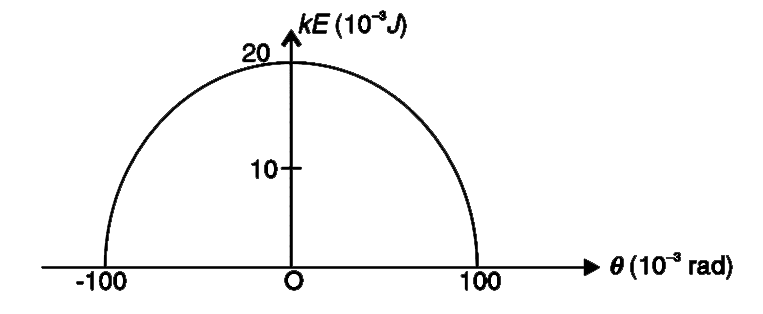
View SolutionThe given figure shows the variation of the kinetic energy of a simple pendulum with its angular displacement `(theta)` from the vertical. Mass of the pendulum bob is m = 0.2 kg. Find the time period of the pendulum. Take `g = 10 ms^(-2)`.
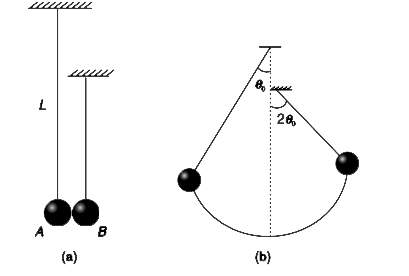
View SolutionTwo identical small elastic balls have been suspended using two strings of different length (see fig (a)). Pendulum A is pulled to left by a small angle `theta_(0)` and released. It hits ball B head on which swings to angle `2 theta _(0)` from the vertical. Calculate the time period of oscillation of A if its length is known to be L.
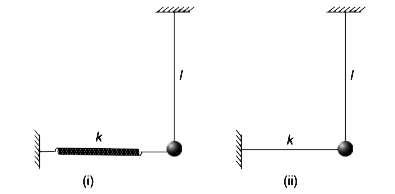
View SolutionA simple pendulum of length L has a bob of mass m. The bob is connected to light horizontal spring of force constant k. The spring is relaxed when the pendulum is vertical (see fig (i)).
(a) The bob is pulled slightly and released. Find the time period of small oscillations. Assume that the spring remains horizontal.
(b) The spring is replaced with an elastic cord of force constant k. The cord is relaxed when the pendulum is vertical (see fig (ii)). The bob is pulled slightly and released. Find the time period of oscillations.
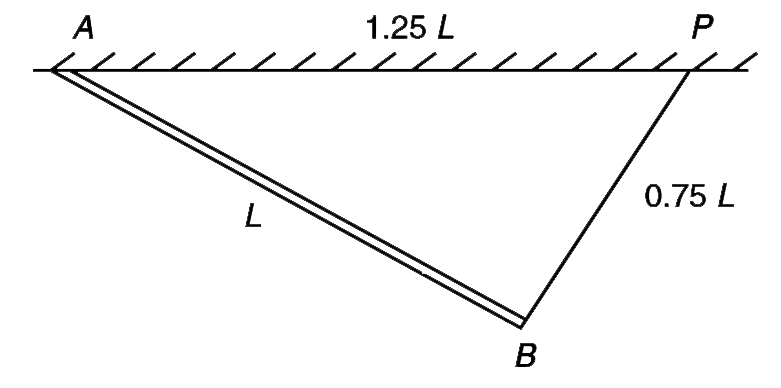
View SolutionA uniform rod AB of mass m and length L is tied, at its end B, to a thread which is attached to point P on the ceiling. Length of the thread PB is 0.75 L. The other end A of the rod is hinged at a point on the ceiling. Distance AP = 1.25 L. End B of the rod is pushed gently perpendicular to the plane of the figure and it starts oscillating
(a) Find the moment of inertia of the rod about line AP.
(b) Assuming that the triangle APB makes a small angle `theta` with the vertical plane, write the restoring torque acting on the rod.
(c ) Calculate the time period of small oscillations.
View SolutionA railway tank wagon with its 2m diameter and 6m long horizontal cylindrical body, half full of petrol is driven around a curve of radius 100m, at a speed of `8.33 m//s`. The curve runs smoothly into a straight track and the train maintains a constant speed. Find the angular amplitude and frequency of subsequent oscillation of the petrol due to this change of motion. Neglect viscosity and consider petrol as a solid semi cylinder sliding inside the tank. Given: `tan^(-1) (0.07) =4^(@)`
View SolutionA pendulum consists of an inextensible thread connected to a solid spherical ball of radius r. The distance between the point of suspension and the centre of the ball is `L (gt gt r)` . Calculate the percentage difference in the time period of this pendulum to the time period of a simple pendulum of length L. How large is this difference for r = 5 cm and L = 100 cm.
View SolutionA disc of radius r is connected to a string of length L. The string is tied to a point on the circumference of the disc. This system is made to oscillate in vertical plane of the disc with a small angular amplitude `theta_(0)`. Find the speed of the lowest point of the disc at the moment the string become vertical.

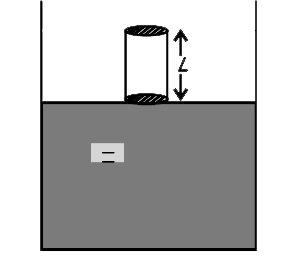
View Solution(i) A cylindrical container has area of cross section equal to 4A and it contains a non viscous liquid of density `2rho`. A wooden cylinder of cross sectional area A and length L has density `rho`. It is held vertically with its lower surface touching the liquid. It is released from this position. Assume that the depth of the container is sufficient and the cylinder does not touch the bottom.
(a) Find amplitude of oscillation of the wooden cylinder.
(b) Find time period of its oscillation.
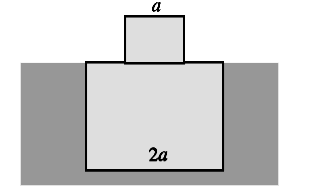
Two cubical blocks of side length a and 2a are stuck symmetrically as shown in the figure. The combined block is floating in water with the bigger block just submerged completely. The block is pushed down a little and released. Find the time period of its oscillation. Neglect viscostiy.
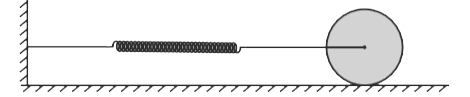
View SolutionA hollow cylindrical shell of radius R has mass M. It is completely filled with ice having mass m. It is placed on a horizontal floor connected to a spring (force constant k) as shown. When it is disturbed it performs oscillations without slipping on the floor.
(a) Find time period of oscillation assuming that the ice is tightly pressed against the inner surface of the cylinder.
(b) If the ice melts into non viscous water, find the time period of oscillations. (Neglect any volume change due to melting of ice)
View SolutionA particle of mass m is free to move along x axis under the influence of a conservative force. The potential energy of the particle is given by `U=-ax^(x) e^(-bx)` [a and b are positive constants]
Find the frequency of small oscillations of the particle about its equilibrium position
View Solution
Level 2 questions and complete solutions for chapter SIMPLE HARMONIC MOTION of ARIHANT PHYSICS (HINGLISH) of Class 11