Complete Solutions to Single correct Answer Type of chapter DIMENSIONS & MEASUREMENT of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | DIMENSIONS & MEASUREMENT |
| CENGAGE PHYSICS | Single correct Answer Type |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
The dimension of `((1)/(2))epsilon_(0)E^(2)` (`epsilon_(0)` : permittivity of free space, E electric field
01:59View SolutionA quantity` X` is given by `epsilon_(p) L(delta V)/(delta t)` , where `epsilon_(p)` is the permitivity of free space ,L is a length , `delta V` is a potential difference and ` deltat ` is a time interval . The dimensional formula for `X` is the same as that of
02:14View SolutionA cube has a side of length `1.2 xx 10^(-2)m`. Calculate its volume.
02:11View SolutionPressure depends on distance as, `P = (alpha)/(beta)exp(-(alphaz)/(ktheta))`, where `alpha, beta` are constants, `z` is distance as , `k` is Boltzman's constant and `theta` is tempreature. The dimension of beta are
03:10View SolutionA wire of length `l = +- 0.06cm` and radius `r =0.5+-0.005 cm` and mass `m = +-0.003gm`. Maximum percentage error in density is
02:59View SolutionWhich of the following sets have different dimensions ?
06:08View SolutionIn a screw gauge, the zero of mainscale coincides with fifth division of circular scale in figure (i). The circular division of screw gauge are `50`. It moves `0.5 mm` on main scale In one rotation. The diameter of the ball in figure (ii) is
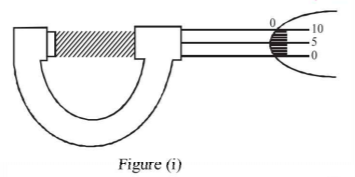
 02:43View Solution
02:43View SolutionAs student performs an experiment for determine of `g[=(4pi^(2)L)/(T^(2))]. L approx 1m`, and has commits an error of `Delta L` for `T` he tajes the teime of `n` osciollations wityh the stop watch of least count `Delta T`. For which of the following data the measurement of `g` will be most accurate?
04:20View SolutionA student performs an experiment to determine the Young's modulus of a wire, exactly`2m` long, by Searle's method. In a partcular reading, the student measures the extension in the length of the wire to be `0.8mm with an uncertainty of `+- 0.05mm` at a load of exactly `1.0kg`, the student also measures the diameter of the wire to be `04mm` with an uncertainty of `+-0.01mm`. Take `g=9.8m//s^(2)` (exact). the Young's modulus obtained from the reading is
04:39View SolutionStudent `I ,II , and III` perform an experiment for measuring the acceleration due to gravity `(g) ` usinf a simple pendulum. They use lengths of the pendulum and // or record time for different number of oscillations . The observations are shown in the following table . Least count for length ` = 0.1 cm`
`{:(underset(III)underset(II)underset(I)underset()underset()("Student"),underset(20.0)underset(64.0)underset(64.0)underset((cm))underset("Pendulam")("Length of "),underset(4)underset(4)underset(8)underset((n))underset("n Oscillation")("Number of"),underset(9.0)underset(16.0)underset(16.0)underset((s))underset("Period")("Time")):}`
Least count for time `= 0.1 s`.
If `E_(I), E_(II)` , and `E_(III)` are the percentage errors in `g` , i.,e., `((Delta g)/( g) xx 100)` for students I,II , and III, respectively , then03:51View SolutionA vernier calipers has `1mm `marks on the main scale. It has `20` equal divisions on the Verier scale which match with `16` main scale divisions. For this Vernier calipers, the least count is
02:56View SolutionThe density of a solid ball is to be determined in an experiment. The diameter of the ball is measured with a screw gauge, whose pitch is `0.5mm` and there are `50` divisions on the circular scale. The reading on the main scale is `2.5mm` and that on circular scale is `20` divisions. if the measured mass of the ball has a relative error of `2%`, the relative percentage error in the density is
04:34View SolutionIn the determination if Young's modulus `((Y = (4MLg)/(pild^(2))` by using searle's method, a wire of length `L=2m` and diameter `d=0.5mm` is used. For a load `M=2.5kg`, an extension `l=0.25mm` in the length of the wire is observed. Quantites `D and l` are measured using a screw gauge and a micrometer, respectively. they have the same pitch of `0.5mm`. the number of divisions on their circular scale is `100`. the contrubution to the maximum probable error of the `Y` measurement
04:34View SolutionThe diameter of a cylinder is measured using a Vernier callipers with no zero error. It is found that the zero of the Vernier scale lies between `5.10cm and 5.15cm` of the main scale. The Vernier scale has `50` divisions equivalent to `2.45 cm`. The `24^(th)` division of the Vernier scale exactly coincides with one of the main scale divisions. the diameter of the cylinder is
05:36View SolutionUsing the expression `2d sin theta = lambda`, one calculates the values of `d` by measuring the corresponding angles `theta` in the range `0 to 90^@`. The wavelength `lambda` is exactly known and error in `theta` is constant for all values of `theta`. As `theta` increases from `0^@`
03:54View Solution
Single correct Answer Type questions and complete solutions for chapter DIMENSIONS & MEASUREMENT of CENGAGE PHYSICS (HINGLISH) of Class 11
