Complete Solutions to Illustration of chapter BASIC MATHEMATICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | BASIC MATHEMATICS |
| CENGAGE PHYSICS | Illustration |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
Calculate `(1001)^(1//3)`.
02:17View SolutionExpand `(1+x)^-3`.
02:42View SolutionThe value of acceleration due to gravity `(g)` at height `h` above the surface of earth is given by
`g^'=(gR^2)/((R+h)^2)`. If `hlt ltR`, then prove that `g^'=g(1-(2h)/(R))`.02:01View SolutionConvert `45^(@)` to radians.
01:15View SolutionConvert `pi//6` radian to degrees.
00:49View SolutionGiven that `sin30^(@)=1//2` and `cos 30^(@)=sqrt3//2`. Determine the values of `sin 60^(@), sin 120^(@), sin 240^(@), sin 300^(@)`, and `sin (-30^(@))`.
04:05View SolutionFind the value of `sin^(-1)1`.
01:00View SolutionFind the value of `cos^-1(-1//2)`.
01:11View SolutionConsider two points `P_1(2,7)` and `P_2(6,15)`. Write the equation and draw a straight line through these points.
02:51View SolutionPlot the line `2x-3y=12`.
02:55View SolutionPlot the line `-3x-5y=15`.
02:06View SolutionPlot a graph for the equation `y=-x^2+4x-1`.
07:37View SolutionPlot a graph for the equation `y=x^2-4x`.
03:58View SolutionA particle starts with uniform acceleration. Draw a graph taking the displacement(s) of the particle along y-axis and time(t) along x-axis. What is the curve known as?
02:07View SolutionA particle starts with some initial velocity with an acceleration along the direction of motion. Draw a graph depicting the variation of velocity (v) along y-axis with the variation of displacement(s) along x-axis.
03:54View SolutionSuppose that the function F is defined for all real numbers r by the formula `f(r)=2(r-1)+3`. Evaluate F at the input values `0, 2, x+2`, and `f(2)`.
02:27View SolutionA function `f(x)` is defined as `f(x)=x^2+3`. Find `f(0), F(1), f(x^2), f(x+1)` and `f(f(1))`.
02:02View SolutionIf `y=x^5`, then find `dy//dx`.
00:38View SolutionIf `y=(1)/(x^10)=x^-10`, then find `dy//dx`.
00:45View SolutionIf `y=(1)/(sqrtx)=(x)^(-1//2)`, then find `dy//dx`.
00:58View SolutionIf `y=3x^2+2x`, then find `dy//dx`.
01:01View SolutionIf `y=4x^4+2x^3+5/x+9`, then find `dy//dx`.
03:06View SolutionFind the derivatives of `y=(x^2+1)(x^3+3)`.
01:46View SolutionIf `y=[3x+2][2x-1]`, then find `(dy)/(dx)`.
01:32View SolutionIf `y=[2x^3+3][2x^-3+1]`, then find `(dy)/(dx)`.
01:34View SolutionFind the derivative of `y=(t^2-1)/(t^2+1)`.
03:17View SolutionIf `y=[(x^2+1)/(x+1)]`, then find `(dy)/(dx)`.
02:33View SolutionIf `y=((x^2+2x))/((3x-4))`, then find `(dy)/(dx)`.
02:34View SolutionIf `y=(sinx)/(x+cosx)`, then find `(dy)/(dx)`.
03:13View SolutionFind the derivative of `y=sin(x^2-4)`.
01:38View SolutionFind the derivative of `y=sqrt(x^2+1)`.
01:57View SolutionIf `y=cos^2x`, then find `(dy)/(dx)`.
01:14View SolutionIf `y=cosx^3`, then find `(dy)/(dx)`.
01:33View SolutionIf `x=at^4`, `y=bt^3`, then find `(dy)/(dx)`.
01:27View SolutionIf `f(x)=xcosx`, find `f''(x)`.
03:21View SolutionFind the minimum and maximum values of the funciton `y=x^3-3x^2+6`. Also find the values of x at which these occur.
05:45View SolutionThe particle's position as a funciton of time is given as `x=5t^2-9t+3`. Find out the maximum value of position co-ordinate? Also, plot the graph.
05:37View SolutionThe velocity v of a particle is given by the equation `v=6t^2-6t^3`, where v is in `ms^-1`, `t` is the instant of time in seconds while 6 and 6 are suitable dimensional constants. At what values of t will the velocity be maximum and minimum? Determine these maximum and minimum values of the velocity.
03:04View SolutionIntegrate the following w.r.t. x.
1. `x^3`
2. `x-1/x`
3. `e^(2x)+(1)/(x^2)`
05:33View SolutionSolve:
1. `int_0^3(ax^2+bx+c)dx`
2. `int_-1^1e^xdx`
3. `int_(-pi//2)^(pi//2) cosx dx`
4. `int_0^10sec^2(3x+6)dx`08:45View SolutionSolve the integral `I=int_0^pisin^2xdx`.
03:19View SolutionSolve the integral `I=int_oo^R(GMm)/(x^2)dx`.
02:41View SolutionEvaluate `intsqrt(1+y^2)*2ydy`
01:40View SolutionEvaluate `int(2zdz)/(root3(z^2+1))`
02:41View SolutionCalculate the area enclosed under the curve `f(x)=x^2` between the limits `x=2` and `x=3` (figure)
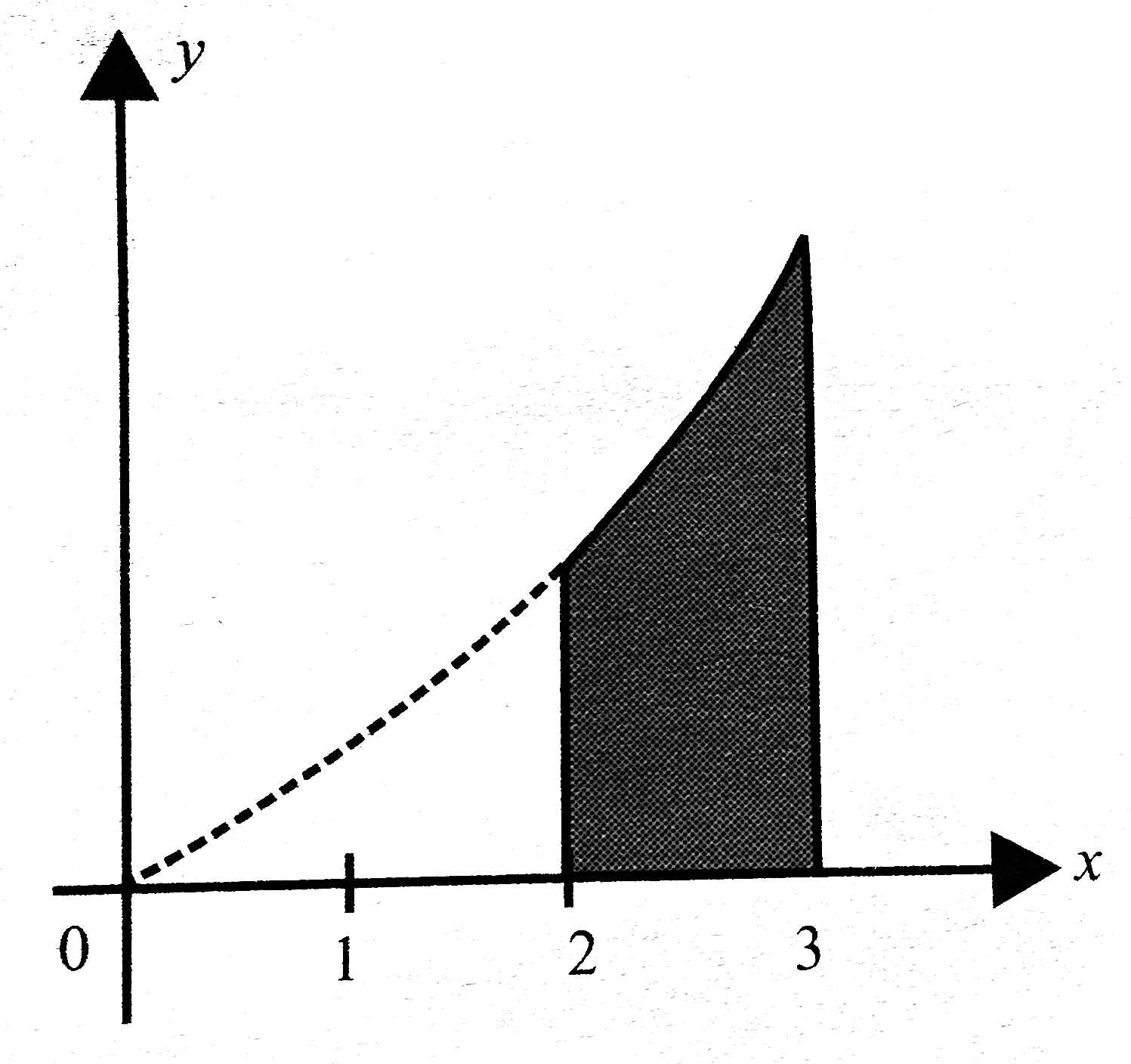 01:51View Solution
01:51View SolutionAt `t=0`, a body starts from origin with some initial velocity. The displacement `x(m)` of the body varies with time `t(s)` as `x=-(2//3)t^2+16t+2`. Find the initial velocity of the body and also find how long does the body take to come to rest? What is the acceleration of the body when it comes to rest?
02:43View SolutionSita is driving along a staight highway in her car. At time `t=0`, when Sita is moving at `10ms^-1` in the positive x-direction, she passes a signpost at `x=50m`. Here acceleration is a function of time:
`a=2.0ms^-2-(1/10ms^-3)t`
a. Derive expressions for her velocity and position as functions of time.
b. At what time is her velocity greatest?
c. What is the maximum velocity?
d. Where is the car when it reaches the maximum velocity?09:34View SolutionA particle starts moving and its displace-ment after `t` seconds is given in meter by the relation `x=5+4t+3t^2`. Calculate the magnitude of its
a. Initial velocity
b. Velocity at `t=3s`
c. Acceleration01:48View SolutionLet the instantaneous velocity of a rocket, just after launching, be given by the expression `v=2t+3t^2` (where v is in `ms^-1` and `t` is in seconds). Find out the distance travelled by the rocket from `t=2s` to `t=3s`.
02:21View SolutionA particle moves with a constant acceleration `a=2ms^-2` along a straight line. If it moves with an initial velocity of `5ms^-1`, then obtain an expression for its instantaneous velocity.
01:17View SolutionIn the previous problem, if the particle occupies a position `x=7m` at `t=1s`, then obtain an expression for the instantaneous displacement of the particle.
01:59View Solution
Illustration questions and complete solutions for chapter BASIC MATHEMATICS of CENGAGE PHYSICS (HINGLISH) of Class 11
