Complete Solutions to Exercise Single Correct of chapter KINEMATICS-2 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS-2 |
| CENGAGE PHYSICS | Exercise Single Correct |
| Number Of Questions | 76 |
| Academic Year | 2023-24 |
Rain is falling vertically downwards with a speed of `4 km h^-1`. A girl moves on a straight road with a velocity of `3 km h^-1`. The apparent velocity of rain with respect to the girl is.
02:47View SolutionShip `A` is travelling with a velocity of `5 km h^-1` due east. A second ship is heading `30^@` east of north. What should be the speed of second ship if it is to remain always due north with respect to the first ship ?
03:30View SolutionA man swims from a point `A` on the bank of a river if width `100 m`. When he swims perpendicular to the water current, he reaches the other bank `50 m` downstream. The angle to the bank at which he should swim, to reach the directly opposite point `B` on the other bank is.
 .View Solution
.View SolutionRain is falling vertically with a velocity of `25 ms^-1`. A woman rides a bicycle with a speed of `10 ms^-1` in the north to south direction. What is the direction (angle with vertical) in which she should hold her umbrella to safe herself from rain ?
03:58View SolutionA police van moving on a highway with a speed of `30 km h^(-1)` Fires a bullet at a thief's car speeding away in a same direction with a speed of `192 km h^(-1)`. If the muzzle speed of the buller is `150 m s^(-1)`, with what speed does the bullet hit thief's car? .
 .04:39View Solution
.04:39View SolutionA bird is flying towards north with a velocity `40 km h^-1` and a train is moving with velocity `40 km h^-1` towards east. What is the velocity of the bird boted by a man in the train ?
03:13View SolutionA river is flowing from west to east at a speed of 5 m/min. A man on the south bank of the river, capable of swimming at 10 m/min in still water, wants to swim across the river in the shortest time. He should swim in a direction.
02:25View SolutionA boat is moving with a velocity `3 hat i+ 4hat j` with respect to ground. The water in the river is moving with a velocity `-3 hat i - 4 hat j` with respect to ground. The relative velocity of the boat with respect to water is.
01:55View SolutionA car is moving towards east with a speed of `25 km h^-1`. To the driver of the car, a bus appears to move towards north with a speed of `25 sqrt(3) km h^-1`. What is the actual velocity of the bus ?
05:13View SolutionA swimmer wishes to cross a `500 - m` river flowing at `5 km h^-1`. His speed with respect to water is `3 km h^-1`. The shortest possible time to cross the river is.
03:12View SolutionA train of `150 m` length is going towards north direction at a speed of `10 ms^-1`. A parrot flies at a speed of `5 ms^-1` towards south direction parallel to the railway track. The time taken by the parrot to cross the train is equal to.
03:47View SolutionA man can swim in still water with a speed of `2 ms^-1`. If he wants to cross a river of water current speed `sqrt(3) ms^-1` along the shortest possible path, then in which direction should he swim ?
05:03View SolutionA truck is moving with a constant velocity of `54 km h^-1`. In which direction (angle with the direction of motion of truck) should a stone be projected up with a velocity of `20 ms^-1`, from the floor of the truck of the truck, so as to appear at right angles to the truck, for a person standing on earth ?
04:38View SolutionA river flows with a speed more than the maximum speed with which a person can swim in still water. He intends to cross the river by the shortest possible path (i.e., he wants to reach the point on the opposite bank which directly opposite to the starting point). Which of the following is correct ?
04:41View SolutionRain, driven by the wind, falls on a railway compartment with a velocity of `20 ms^-1`, at an angle of `30^@` to the vertical. The train moves, along the direction of wind flow, at a speed of `108 km h^-1`. Determine the apparent velocity of rain for a person sitting in the train.
05:34View SolutionThe ratio of the distance carried away by the water current, downstream, in crossing a river, by a person, making same angle with downstream and upstream is `2 : 1`. The ratio of the speed of person to the water current cannot be less than.
06:21View SolutionA particle is moving in a circle of radius `r` centred at `O` with constant speed `v`. What is the change in velocity in moving from `A` to `B` `(/_ AOB = 40^@)` ?
03:58View SolutionA particle is projected with a velocity `v` so that its range on a horizontal plane is twice the greatest height attained. If `g` is acceleration due to gravity, then its range is
03:15View SolutionFind the angle of projection of a projectile for which the horizontal range and maximum height are equal.
02:01View SolutionA particle is projected from ground at some angle with the horizontal. Let `P` be the point at maximum height `H`. At what height above the point `P` should the particle be aimed to have equal to maximum height ?
04:09View SolutionThe height `y` and the distance `x` along the horizontal plane of a projectile on a certain planet (with no surrounding atmosphere) are given by `y = (8t - 5t^2) m` and `x = 6tm`, where `t` is in seconds. The velocity with which the projectile is projected at `t = 0` is.
02:46View SolutionIn the above problem, what is the angle of projection with horizontal ?
05:45View SolutionA shot is fired from a point at a distance of `200 m` from the foot of a tower `100 m` high so that it just passes over it horizontally. The direction of shot with horizontal is.
05:32View SolutionTwo bullets are fired simultaneously, horizontally and with different speeds from the same place. Whch bullet will hit the ground first?
02:17View SolutionThe maximum height reached by projectile is `4 m`. The horizontal range is `12 m`. The velocity of projection in `m s^-1` is (g is acceleration due to gravity)
05:50View SolutionA ball thrown by one player reaches the other in `2 s`. The maximum height attained by the ball above the point of projection will be about.
02:16View SolutionA projectile has a time of flight `T` and range `R`. If the time of flight is doubled, keeping the angle of projection same, what happens to the range ?
03:16View SolutionA ball is thrown from a point with a speed 'v^(0)' at an elevation angle of `theta` . From the same point and at the same instant , a person starts running with a constant speed `('v_(0)')/(2) ` to catch the ball . Will the person be able to catch the ball ? If yes, what should be the angle of projection `theta` ?
02:38View SolutionA body is projected at an angle of `30^@` with the horizontal and with a speed of `30 ms^-1`. What is the angle with the horizontal after `1.5 s` ? `(g = 10 ms^-2)`.
02:32View SolutionA grasshopper can jump a maximum distance `1.6 m`. It spends negligible time on the ground. How far can it go in `10 s` ?
02:21View SolutionA body has an initial velocity of `3 ms^-1` and has an acceleration of `1 ms^-2` normal to the direction of the initial velocity. Then its velocity `4 s` after the start is.
03:08View SolutionTwo tall buildings are `30 m` apart. The speed with which a ball must be thrown horizontally from a window `150 m` above the ground in one building so that it enters a window `27.5 m` from the ground in the other building is.
04:37View SolutionA shell fired from the ground is just able to cross horizontally the top of a wall `90 m` away and `45 m` high. The direction of projection of the shell will be.
03:28View SolutionTwo paper screens A and B are separated by 150m. A bullet pierces A and B. The hole in B in 15 cm below the hole in A. If the bullet is travelling horizontally at the time of hitting A, then the velocity of the bullet at A is: `(g=10ms^(-2))`
04:22View SolutionA projectile can have same range `R` for two angles of projection. It `t_1 and t_2` are the times of flight in the two cases, then what is the product of two times of flight ?
03:28View SolutionA ball is thrown at different angles with the same speed `u` and from the same points and it has same range in both the cases. If `y_1 and y_2` be the heights attained in the two cases, then find the value of `y_1 + y_2`.
04:08View SolutionThe equation of motion of a projectile is `y = 12 x - (3)/(4) x^2`. The horizontal component of velocity is `3 ms^-1`. What is the range of the projectile ?
03:01View SolutionTwo particles are projected obliquely from ground with same speed such that their range `'R'` are same but they attain different maximum heights `h_(1)` and `h_(2)` then relation between `R, h_(1)` and `h_(2)` is:
03:51View SolutionAt what angle with the horizontal should a ball be thrown so that the range `R` is related to the time of flight as `R = 5 T^2` ? `(Take g = 10 ms^(-2))`.
02:50View SolutionA ball thrown by one player reaches the other in `2 s`. The maximum height attained by the ball above the point of projection will be about.
02:16View SolutionA ball rolls off the top of a staircase with a horizontal velocity `u m//s`. If the steps are h meter high and b meter wide, the ball will hit the edge of the nth steps, if:
03:28View SolutionAt a height `0.4 m` from the ground the velocity of a projectile in vector form is `vec v = (6 hat i+ 2 hat j) ms ^-1`. The angle of projection is
03:47View SolutionA projectile is thrown in the upward direction making an angle of `60^@` with the horizontal direction with a velocity of `150 ms^-1`. Then the time after which its inclination with the horizontal is `45^@` is
06:06View SolutionA gun is firing bullets with velocity `v_0` by rotating it through `360^@` in the horizontal plane. The maximum area covered by the bullets is
04:47View SolutionA person sitting in the rear end of the compartment throws a ball towards the front end. The ball follows a parabolic path. The train is moving with uniform velocity of `20ms^(-1)`. A person standing outside on the ground also observers the ball. How will the maximum heights `(h_(m))` attained and the ranges (R) seen by thrower and the outside observer compare each other?
04:51View SolutionTwo stones are projected with the same speed but making different angles with the horizontal. Their horizontal ranges are equal. The angle of projection of one is `pi/3` and the maximum height reached by it is 102 m. Then the maximum height reached by the other in metres is
02:02View SolutionA ball is projected from the ground at angle `theta` with the horizontal. After `1 s`, it is moving at angle `45^@` with the horizontal and after `2 s` it is moving horizontally. What is the velocity of projection of the ball ?
05:15View SolutionA body is projected horizontally from the top of a tower with initial velocity `18 m s^-1`. It hits the ground at angle `45^@`. What is the vertical component of velocity when it strikes the ground ?
02:13View SolutionA plane flying horizontally at `100 m s^-1` releases an object which reaches the ground in `10 s`. At what angle with horizontal it hits the ground ?
04:16View SolutionA hose lying on the ground shoots a stream of water upward at an angle of `60^@` to the horizontal with the velocity of `16 m s^-1`. The height at which the water strikes the wall `8 m` away is.
04:37View SolutionShow that there are two values of time for which a projectile is at the same height. Also show mathematically that the sum of these two times is equal to the time of flight.
02:51View SolutionA golfer standing on level ground hits a ball with a velocity of `52 m s^-1` at an angle `theta` above the horizontal. If `tan theta = 5//12`, then find the time for which then ball is atleast `15 m` above the ground `(take g = 10 m s^-2)`.
03:54View SolutionA body is projected up a smooth inclined plane with velocity V from the point A as shown in the figure. The angle of inclination is `45^(@)` and the top is connected to a well of diameter 40m. If the body just manages to across the well, what is the value of V? Length of inclined plane is `20sqrt(2)m`.
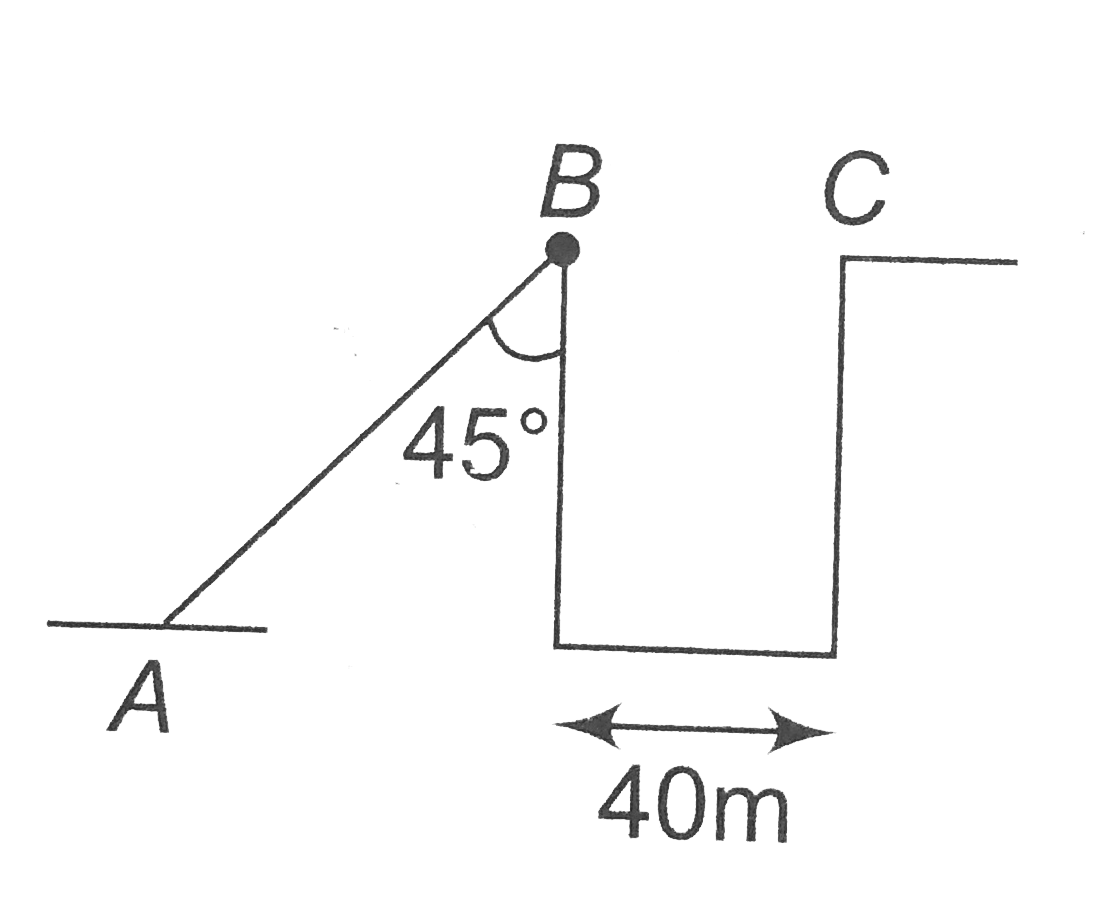 03:29View Solution
03:29View SolutionA rifle shoots a bullet with a muzzle velocity of `400 m s^-1` at a small target `400 m` away. The height above the target at which the bullet must be aimed to hit the target is `(g = 10 m s^-2)`.
03:55View SolutionA projectile is fired from level ground at an angle `theta` above the horizontal. The elevation angle `phi` of the highest point as seen from the launch point is related to `theta` by the relation.
02:57View SolutionA projectile has initially the same horizontal velocity as it would acquire if it had moved from rest with uniform acceleration of `3 m s^-2` for `0.5 min`. If the maximum height reached by it is `80 m`, then the angle of projection is `(g = 10 ms^-2)`.
03:55View SolutionIf a stone is to hit at a point which is at a distance `d` away and at a height `h` (Fig. 5.200) above the point from where the stone starts, then what is the value of initial speed `u` if the stone is launched at an angle `theta` ?
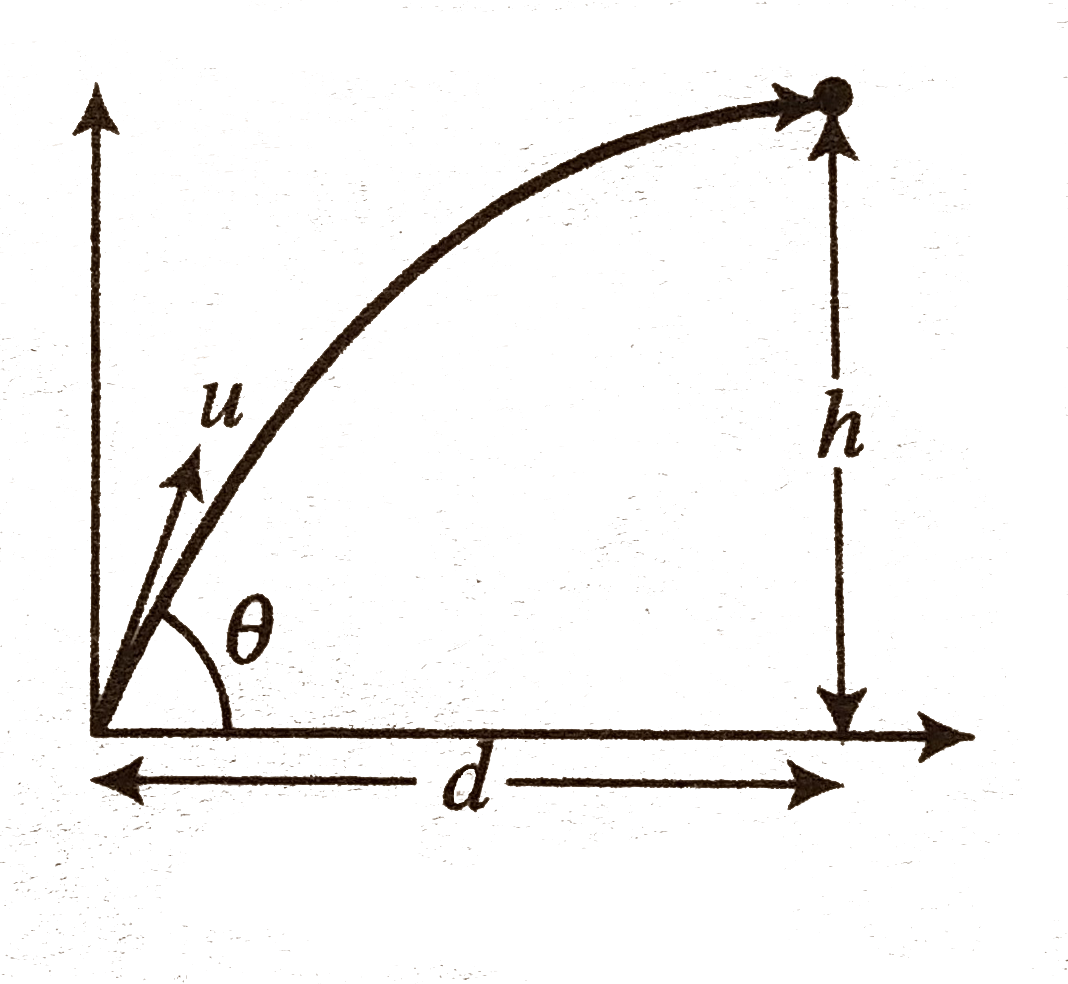 .05:08View Solution
.05:08View SolutionThe speed of a projectile at its maximum height is `sqrt3//2` times its initial speed. If the range of the projectile is n times the maximum height attained by it, n is equal to :
03:46View SolutionThe trajectory of a projectile in a vertical plane is `y = ax - bx^2`, where `a and b` are constant and `x and y` are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.
03:22View SolutionA projectile is given an initial velocity of ` ( hat(i) + 2 hat (j) ) m//s`, where ` hat(i)` is along the ground and `hat (j)` is along the vertical . If ` g = 10 m//s^(2) `, the equation of its trajectory is :
02:30View SolutionAverage velocity of a particle in projectile motion between its starting point and the highest point of its trajectory is (projectin speed = u, angle projection from horizontal =`theta`)
03:31View SolutionTwo balls `A and B` are thrown with speeds `u and u//2`, respectively. Both the balls cover the same horizontal distance before returning to the plane of projection. If the angle of projection of ball `B is 15^@` with the horizontal, then the angle of projection of `A` is.
03:04View SolutionA body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If a second body of mass 2m is projected horizontally from the top of a tower of height 2h, it reaches the ground at a distance 2x from the foot of the tower. The horizontal velocity of the second body is :
05:26View SolutionA car is moving horizontally along a straight line with a unifrom velocity of `25 m s^-1`. A projectile is to be fired from this car in such a way that it will return to it after it has moved `100 m`. The speed of the projection must be.
02:27View SolutionThe horizontal range and miximum height attained by a projectile are `R and H`, respectively. If a constant horizontal acceleration `a = g//4` is imparted to the projectile due to wind, then its horizontal range and maximum height will be
05:19View SolutionA particle is projected with a certain velocity at an angle `prop` above the horizontal from the foot of an inclined plane of inclination `30^@`. If the particle strikes the plane normally, then `prop` is equal to.
05:39View SolutionIn the time taken by the projectile to reach from `A` to `B` is `t`. Then the distance `AB` is equal to.
 .03:11View Solution
.03:11View SolutionA motor cyclist is trying to jump across a path as shown by driving horizontally off a cliff A at a speed of `5ms^(-1)`. Ignore air resistance and take `g=10ms^(-2)`. The speed with which he touches the peak B is:
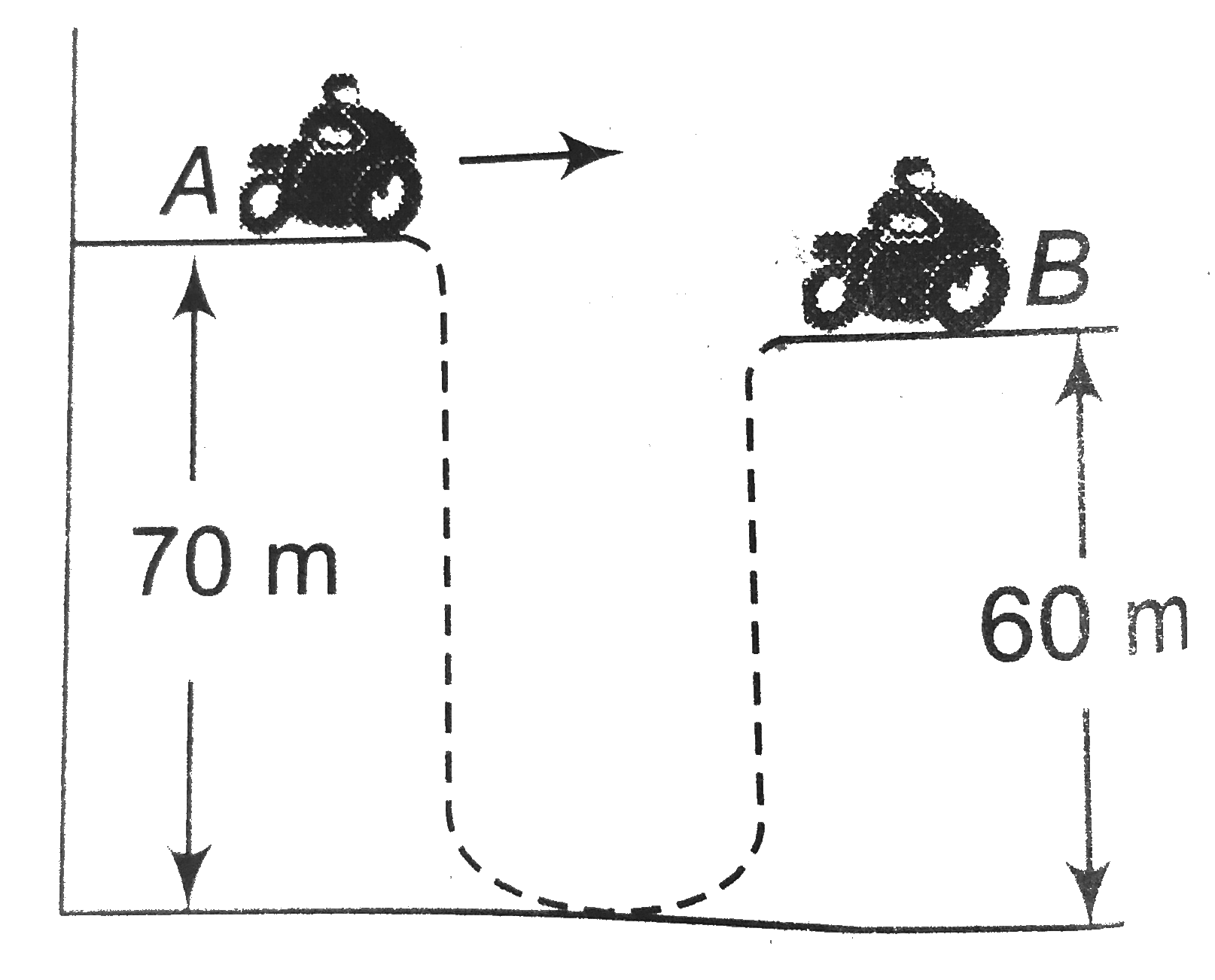 02:21View Solution
02:21View SolutionThe height `y` nad the distance `x` along the horizontal plane of a projectile on a certain planet (with no surrounding atmosphere) are given by `y = (8t - 5t^2) m` and `x = 6t m`, where `t` is in seconds. The velocity with which the projectile is projected at `t = 0` is.
02:46View SolutionA particle `P` is projected with velocity `u_1` at an angle of `30^@` with the horizontal. Another particle `Q` is thrown vertically upwards with velocity `u_2` from a point vertically below the highest point of path of `P`. Determine the necessary condition for the two particles to collide at the highest point.
 .04:04View Solution
.04:04View SolutionA ball is projected from a point `A` with some velocity at an angle `30^@` with the horizontal as shown in (Fig. 5.204). Consider a target at point `B`. The ball will hit the target if it thrown with a velocity `v_0` equal to.
 .04:58View Solution
.04:58View SolutionA body is moving in a circle with a speed of `1 ms^-1`. This speed increases at a constant rate of `2 ms^-1` every second. Assume that the radius of the circle described is `25 m`. The total accleration of the body after `2 s` is.
02:55View SolutionA body is moving in a circular path with a constant speed. It has .
03:28View SolutionA particle is moving along a circular path with uniform speed. Through what angle does its angular velocity change when it completes half of the circular path ?
02:43View SolutionA particle is moving along a circular path. The angular velocity, linear velocity,. Angular acceleration, and centripetal acceleration of the particle at any instant. Respectively are `vec omega, vec v, vec prop, and vec a_c`. Which of the following relations is not correct ?
View SolutionThe angular velocity of a particle moving in a circle of radius `50 cm` is increased in 5 min from `100` revolutions per minute to `400` revolutions per minute. Find the tangential acceleration of the particle.
03:07View Solution
Exercise Single Correct questions and complete solutions for chapter KINEMATICS-2 of CENGAGE PHYSICS (HINGLISH) of Class 11
