Complete Solutions to Exercise Comprehension of chapter KINEMATICS-2 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | KINEMATICS-2 |
| CENGAGE PHYSICS | Exercise Comprehension |
| Number Of Questions | 21 |
| Academic Year | 2023-24 |
A car is moving towards south with a speed of `20 m s^(-1)`. A motorcyclist is moving towards east with a speed of `15 s^(-1)`. At a certain instant, the motorcyclist is due south of the car and is at a distance of `50 m`from the car.
The shortest distance between the motorcyclist and the car is.
View SolutionA car is moving towards south with a speed of `20 m s^(-1)`. A motorcyclist is moving towards east with a speed of `15 m s^(-1)`. At a certain instant, the motorcyclist is due south of the car and is at a distance of `50 m` from the car.
The time after which they are closest to each other.
View SolutionA man can swim at a speed of `3 km h^-1` in still water. He wants to cross a `500-m` wide river flowing at `2 km h^-1`. He keeps himself always at an angle to `120^@` with the river flow while swimming.
The time taken to cross the river is.
View SolutionA man can swim at a speed of `3 km h^-1` in still water. He wants to cross a `500-m` wide river flowing at `2 km h^-1`. He keeps himself always at an angle to `120^@` with the river flow while swimming.
The drift of the man along the direction of flow, when he arrives at the opposite bank is.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle `30^@` with the vertical. As he starts moving forward with a speed of `0.5 m s^-1`, he finds that the rain is falling vertically.
The speed of rain with respect to the stationary man is.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle `30^@` with the vertical. As he starts moving forward with a speed of `0.5 m s^-1`, he finds that the rain is falling vertically.
The speed of rain with respect to the moving man is.
View SolutionFrom a tower of height `40 m`, two bodies are simultaneously projected horizontally in opposite direction, with velocities `2 m s^-1 and 8 ms^-1`. respectively.
The time taken for the velocity vectors of two bodies to become perpendicular to each other is :
View SolutionFrom a tower of height `40 m`, two bodies are simultaneously projected horizontally in opposite direction, with velocities `2 m s^-1 and 8 ms^-1`. respectively.
The horizontal distance between two bodies, when their velocity are perpendicular to each other, is.
View SolutionFrom a tower of height `40 m`, two bodies are simultaneously projected horizontally in opposite direction, with velocities `2 m s^-1 and 8 ms^-1`. respectively.
The time taken for the displacement vectors of two bodies to be come perpendicular to each other is.
View SolutionA ball is thrown from a point in level with velocity `u` and at a horizontal distance `r` from the top os a tower of height `h`.
How must the speed and angle of the projection of the ball be related to `r` in order that the ball may just go grazing the top edge of the tower ?
View SolutionA ball is thrown from a point in level with velocity `u` and at a horizontal distance `r` from the top of a tower of height `h`.
At what horizontal distance `x` from the foot of the tower does the ball hit the ground ?
View SolutionA `0.098-kg` block slides down a frictionless track as shown in (Fig. ).
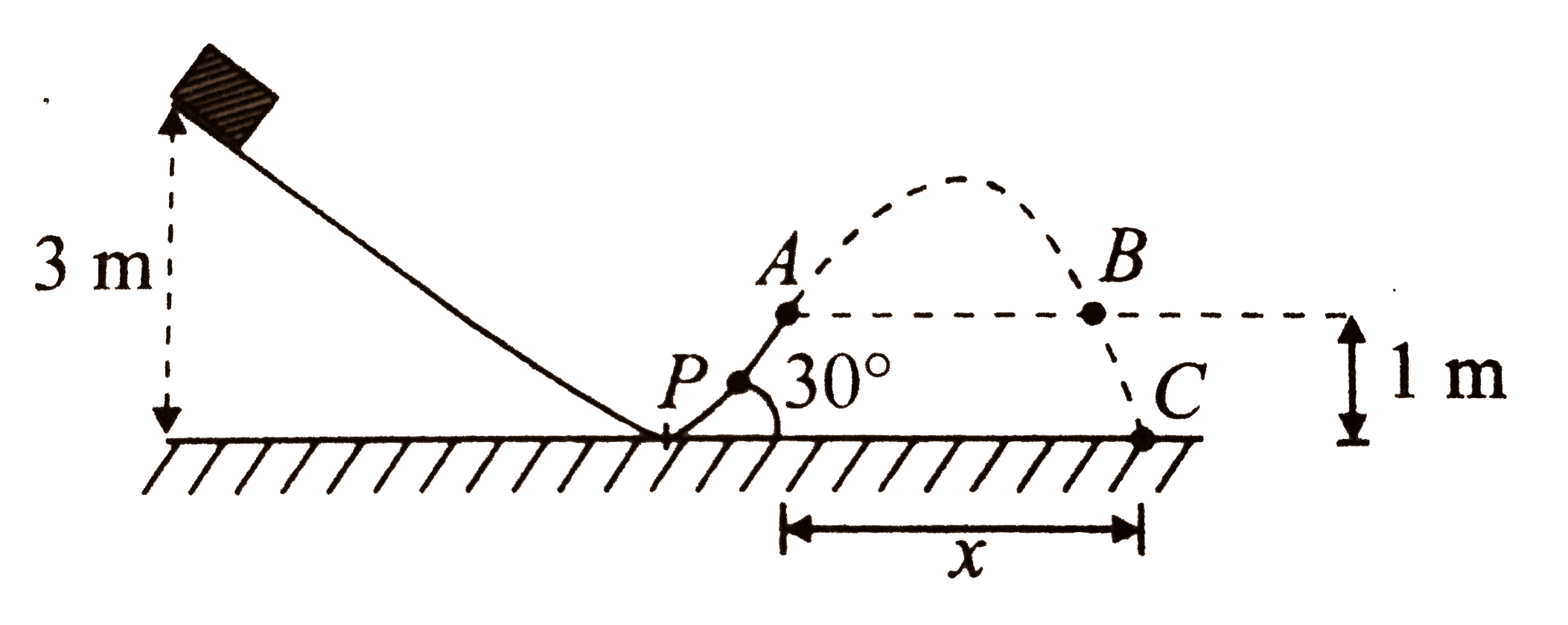 .
.
The vertical component of the velocity of block at `A` is
View SolutionA `0.098-kg` block slides down a frictionless track as shown in (Fig. 5.208).
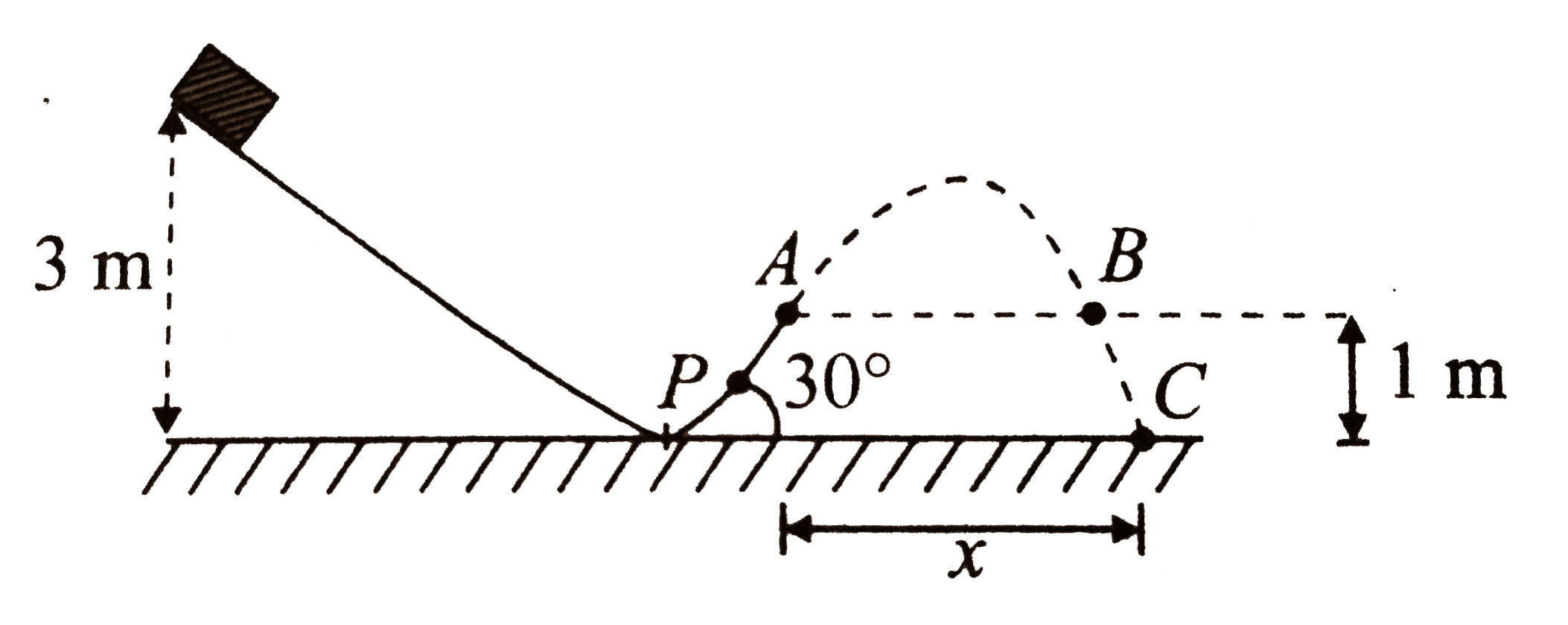 .
.
The time taken by the block to move from `A` to `B` is.
View SolutionA `0.098-kg` block slides down a frictionless track as shown in (Fig. 5.208).
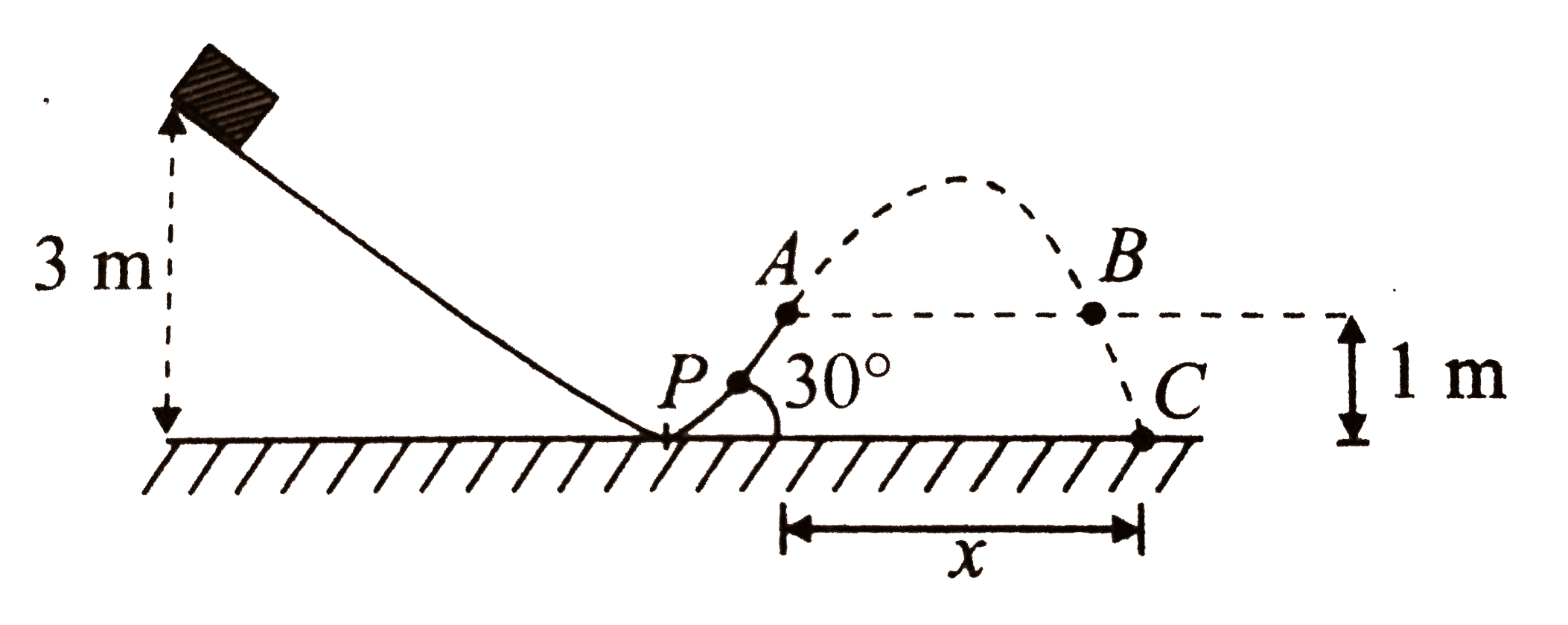 .
.
The time taken by the block to move from `A` to `C` is.
View SolutionA `0.098-kg` block slides down a frictionless track as shown in (Fig. 5.208).
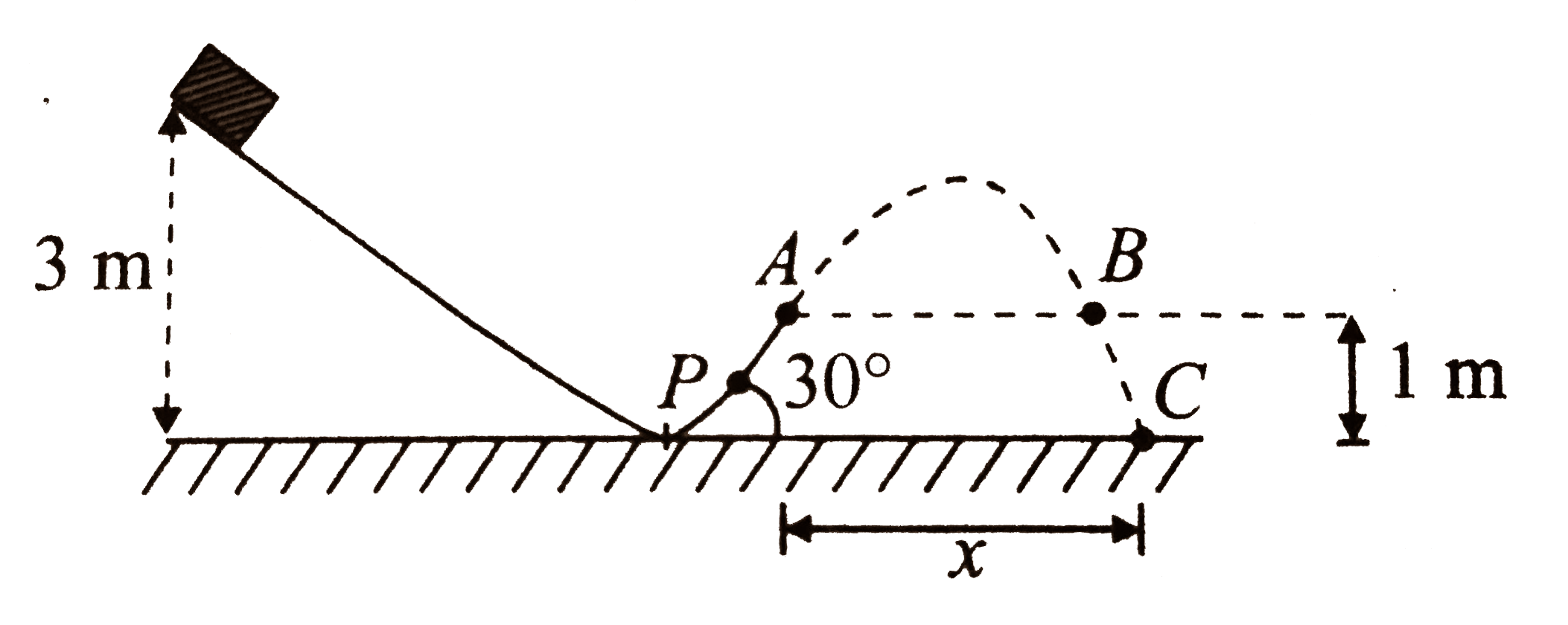 .
.
The horizontal distance `x` travelled by the block in moving from `A` to `C` is.
View SolutionA projectile is thrown with velocity `v` at an angle `theta` with the horizontal. When the projectile is at a height equal to half of the maximum height,.
The vertical component of the velocity of projectile is.
View SolutionA projectile is thrown with velocity `v` at an angle `theta` with the horizontal. When the projectile is at a height equal to half of the maximum height,.
The velocity of the projectile when it is at a height equal to half of the maximum height is.
View SolutionA body is thrown at an angle `theta_0` with the horizontal such that it attains a speed equal to `(sqrt((2)/(3))` times the speed of projection when the body is at half of its maximum height. Find the angle `theta_0`.
View SolutionA particle is projected with a speed u at angle `theta` with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circle? This radius is called the adius of curvature of the curve at the point.
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes and angle `theta/2` with the horizontal?
View SolutionA particle is projected with a speed `u` at an angle `theta` to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height `H` attained by it.
View Solution
Exercise Comprehension questions and complete solutions for chapter KINEMATICS-2 of CENGAGE PHYSICS (HINGLISH) of Class 11