Complete Solutions to Exercise 7.3 of chapter NEWTON'S LAWS OF MOTION 2 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTON'S LAWS OF MOTION 2 |
| CENGAGE PHYSICS | Exercise 7.3 |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
Three masses are atteched to strings rotaing in the horizontal plank .The string pass over two naine as shown in fig will this system be in equilibrium
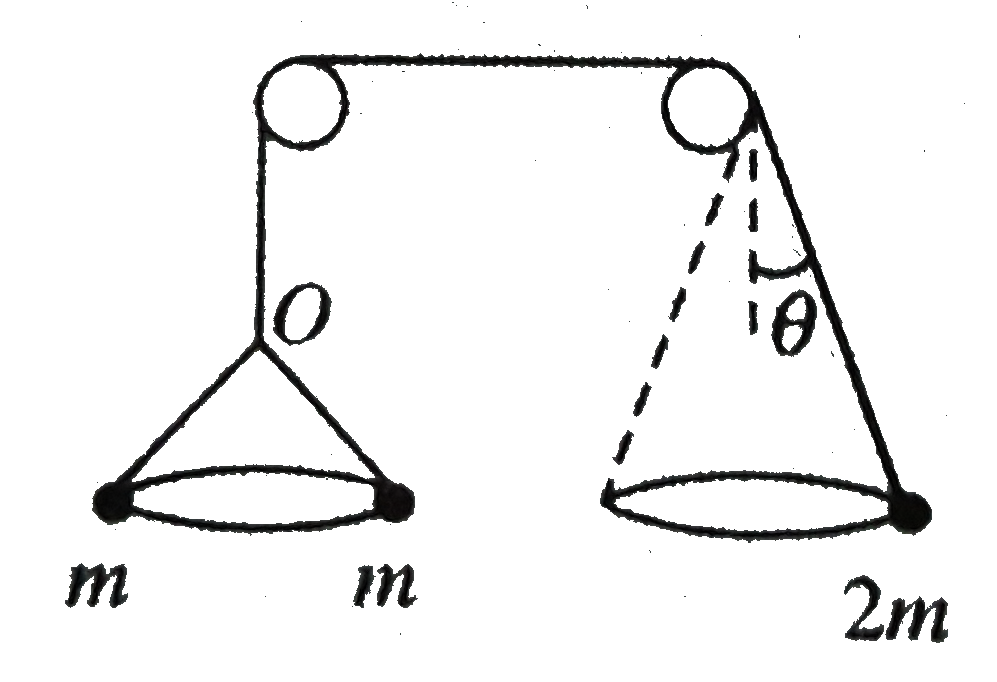 04:10View Solution
04:10View SolutionCan force determine the direction of motion ? Direction of acceleration ?
02:42View SolutionYour are riding on a Ferris wheel that is rotating with a constant speed . The car in which you are riding always maintain its correct upward orientation , it does not invert.
a. What is the direction of the normal force on you form the seat when you are at the top of the wheel ?
i. upward ii. downward .iii. impossible to determine
b. From the same choices, what is the direction of the net force on you when you are at the top of the wheel?02:51View SolutionA bead slide freely along a curved wire lying on a horizontal surface at constant speed as shown in Fig
a. Draw the vectors repesenting the force exerted by the wire on the bead at point A ,B and C
b. Suppose the bead in figure speeds up with constant tangential acceleration as it moves toward the right Draw the vector representing the force on the bead at point A B and C
 05:33View Solution
05:33View SolutionA smooth block loosely fits in a circular tube placed on a horizontal surface . The block moves along the tube (fig ) Which wall (inner or outer) will exert a non zero normal contact force on the block?
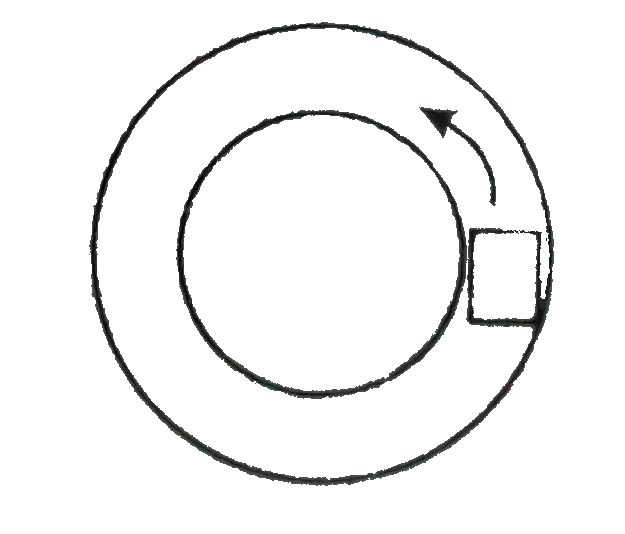 02:44View Solution
02:44View SolutionAn amusement park ride consist of a large verticle cylinder that spins about its axis first fast enough that any person inside is held up againest the wall when the is `mu_(s)` and the radius of the cylider is R

a. Shown that maximum period of revolation neccessary to keep the person from falling is `T = (4 pi^(2) mu_(s) //g)^(1//2)`
b. Obtain a numerical value for taking `R = 4.00m` and `mu_(s) = 0.400` . How many revolations per minute does the cylinder make?
c.If the rate of revolation of the cylinder is make to be some what larger what happens to the magnitude of each one of the forces acting on the person ? What happens to the motion of the person ?
d.If instead the cylinder rate revolation is made to be somewhat smaller what happens to the magnitude happens to the motion of the person ?05:29View SolutionTarzan `(m = 85.0 kg)` tries to cross a river by swinging on a vine . The vine is `10.0m` just and his speed at the bottom of the swing (as he just clears the water) will be `8.00 ms^(-1)` Tarzan does not know that the vine hasa breaking strenght of `1000 N` Does he make it across the river safely ?
03:29View SolutionA roller -coaster car a mass of `500 kg` when fully loaded with passengers

a. If the vehicle has a speed of `20.0ms^(-1)` at point what is the force exerted by the track on the car at this point ?
b. What is the maximum speed the vehicle can have point B and still remain on the track?03:59View SolutionAn air puck of mass `m_(1)` is tied to a string allowed to revolved in a circle of radius `R` on a frictionless horizontal table . The other end of the string passes through a small hole in the centre of the table , and a load of mass `m_(2)` is tied to the string? The suspended load remains in equilibrium while the pack on the tabletop revolves.

a. Find the tension in the string
b. Find the radial force acting on the puck
c. Find the speed of the puck
d. Qualitaively describe what will happen in the monsion of the puck if the value of `m_(2)` is somewhat increased by placing an additional load on it.
e.Qualitaively describe what will happen in the monsion of the puck if the value of `m_(2)` is instead decreased removing a part from the hanging load.05:19View SolutionA sleeve `A` can slide freely along a smooth rod bent in the shape of a half circle of radius `R` .The system is set in rotaion with a constant angular velocity `omega` about a vertical axis `OO'` .Find the angle `theta` corresponding to the steady position of the sleeve
 02:19View Solution
02:19View SolutionA ball suspended by a thread swings ia a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle `theta` of thread deflection in the extreme position will be
05:11View SolutionA simple pendulum is oscillating with angular displacement `90^(@)` For what angle with vertical the acceleration of bob direction horizontal?
04:08View SolutionA ceiling fan has a diameter (of the circle through the outher edges of three blocks ) of `120 cm` and rpm `1500` at fall speed consider a partical of mass `1g` stiking at the outer end of a blade.
a. How much force does it experience the fan runs at falll speed ?
b.Who exerts this force on the partical ?
c. How much force does not the particle exert on the blade along its surface?03:23View SolutionA block of mass `m` is kept on a horizontal ruler . The friction coefficient between the ruler and the block is `m` . The ruler is fixed at one end the block is at a distance L from the fixed end . The ruler is rotated about the fixed end in the horizontal plane through the fixed end
a. What can the maximum angular speed be for which the block does not slip?
b. If the angular speed of the ruler is uniform increase from zero at an angular acceleration a at angular speed will the block slip?09:47View SolutionAn old record player of `15.0 cm` radius at `33.0"rev" min^(1)` while mounted on a `30^(@)` incline as shown in figure

a. If a mass `m` can be placed anywhere on the rotaing record , where is the most critical place on the disc where slipping might occur ?
b.Calculate the least possible coefficient of friction that must exist if no slipping occurs.05:30View SolutionA `60-kg` woman is on a large vertical swing of radius `20 m` . The swing rotates with constant speed
a. At what speed would she feel weightless at the top?
b. At this speed what is her apparent weight at the bottom?02:32View SolutionA rod `OA` rotates about a horizontal axis through `O` with a constant aniclockwise velocity `omega = 3 red s^(-1)`. As it passes the position `theta = 0`, a small block of mass `m` is placed on it at a radial distance `r = 450 mm` if the block is observed to slip at `theta = 50^(@)` . Find the coefficient of static friction between the block and the rot
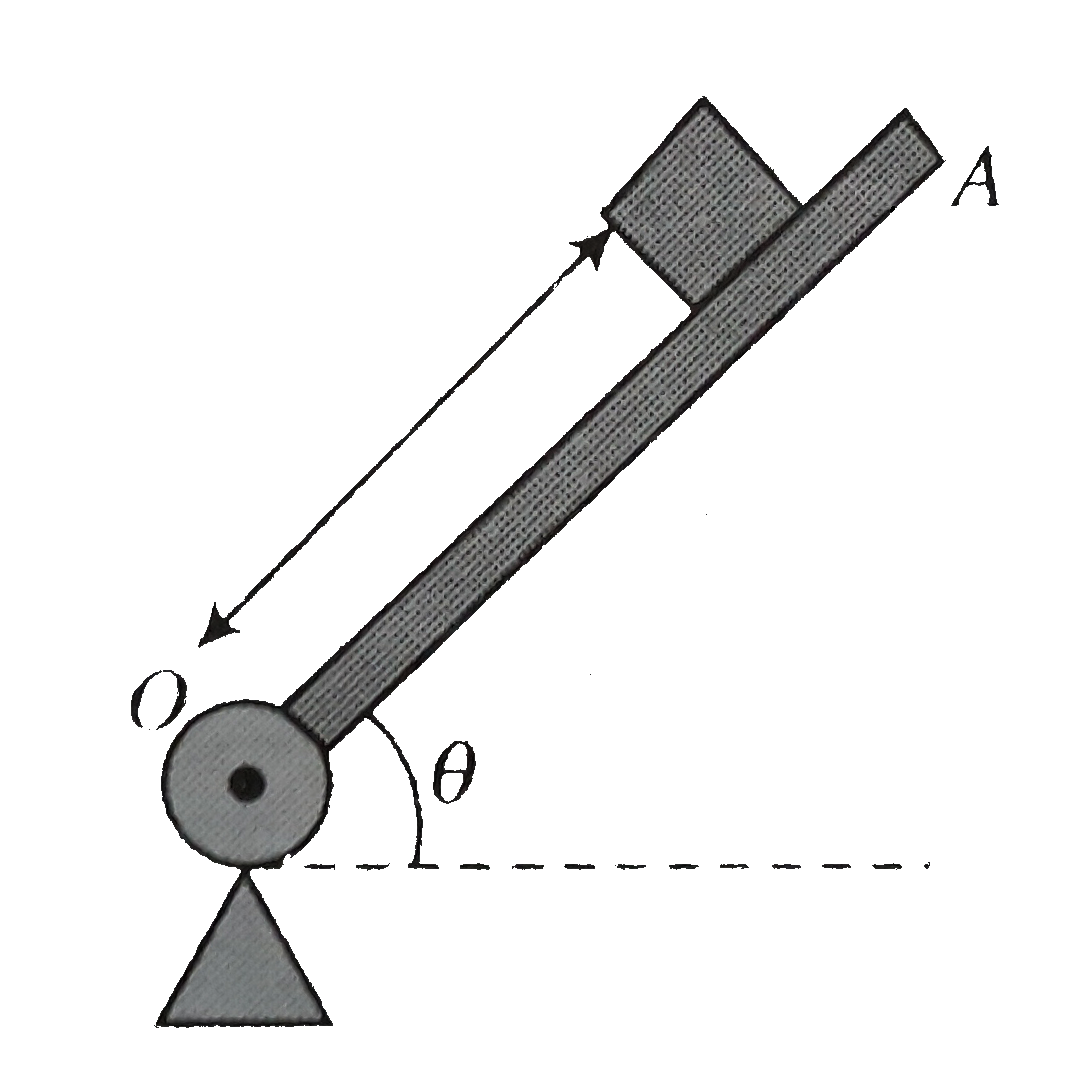
(Given that `sin 50^(@) = 0.766, cos 50^(@) = 0.64)`03:32View SolutionA small mass `m` and its supporting wire because a simple pendulum when the horizontal cord is cut . Find the ratio of the tension in the supporting wire immediately after the cord is cut to the tension in the wire before the cord is cut
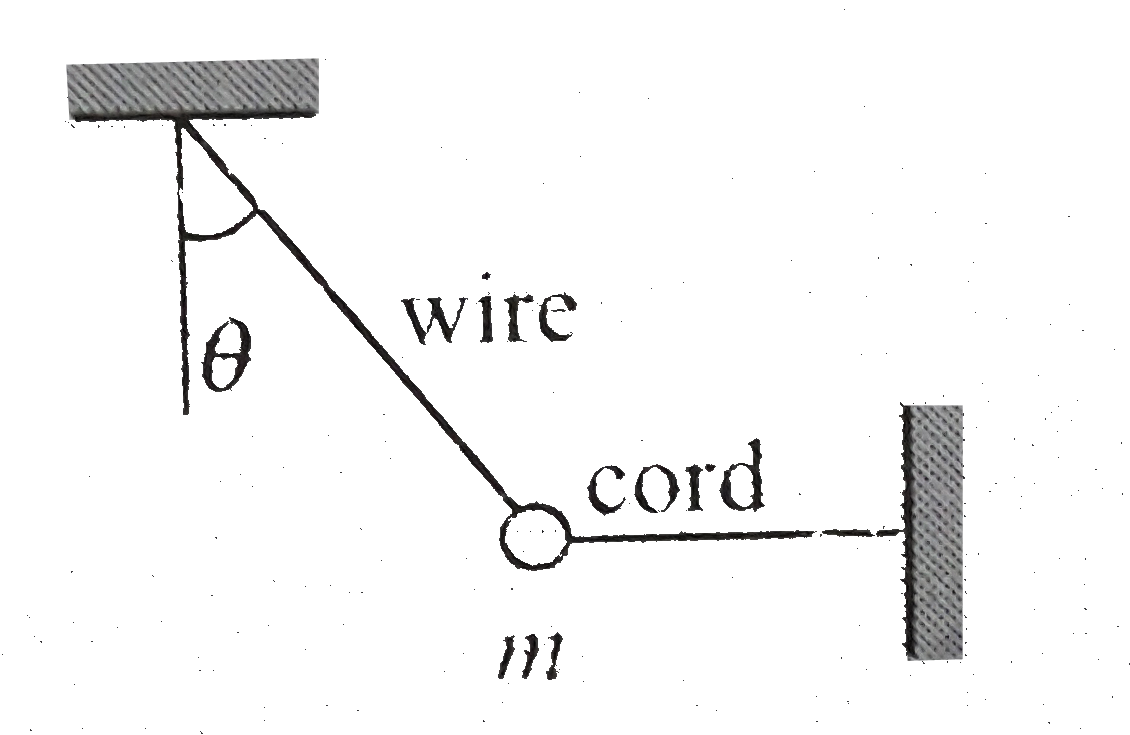 03:58View Solution
03:58View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle `theta` with the vertical. Find the tension in the string at this instant.
02:36View SolutionA car is moving with uniform speed over a circular bridge of radius `R` which subtends an angle of `90^(@)` at its center. Find the minimum posible speed so that the car can cross the bridge without losing the contact any where
03:36View SolutionA block of mass `m` fitted with a light spring of stiffness k and natural length `l_(0)` kept on a smooth radial groove made on a disc rotaing with a constant angular axis . If the block is released slowly . Find the maximum elongation of the spring
 02:23View Solution
02:23View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is `mu_(s)` .Find the velocity of the before it start sliding relative as the disc
 02:40View Solution
02:40View SolutionThere are two blocks of masses `m_(1)` and `m_(2) , m_(1)` is placed on `m_(2)` on a table which is rotating with an angular velocity `omega` about the vertical axis . The coefficent of friction between the block is `mu_(1)` and between `m_(2)` and table is `mu_(2) (mu_(1) lt mu_(2))` if block are placed at distance R from the axis of ratation , for relative sliding between the surface in contact , find the
a. friction force at the contacting surface
b. maximum angular speed `omega`
 02:31View Solution
02:31View SolutionA small wedge whose base is horizontal is fixed to a vertical rod as shown in fig . The sloping side of the weidgeis frictionless and the wedge is span with a constant angular speed `omega` about vertical axis as shown in the fig find the
a. value of angular speed `omega ` for which the block of mass `m` just does not slide down the wedge.
b. normal reaction on the block by wedge when block does not slip relative to wedge.
 03:19View Solution
03:19View SolutionA table with smooth horizontal surface is turning at an angular speed `omega` about its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
04:49View SolutionA table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity `omega` in a circular pathof radius R. A smooth groove AB of length `L(ltltR)` is made on the surface of the table. The groove makes an angle` theta` with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move along AB. Find the time taken by tehparticle to reach the point B.
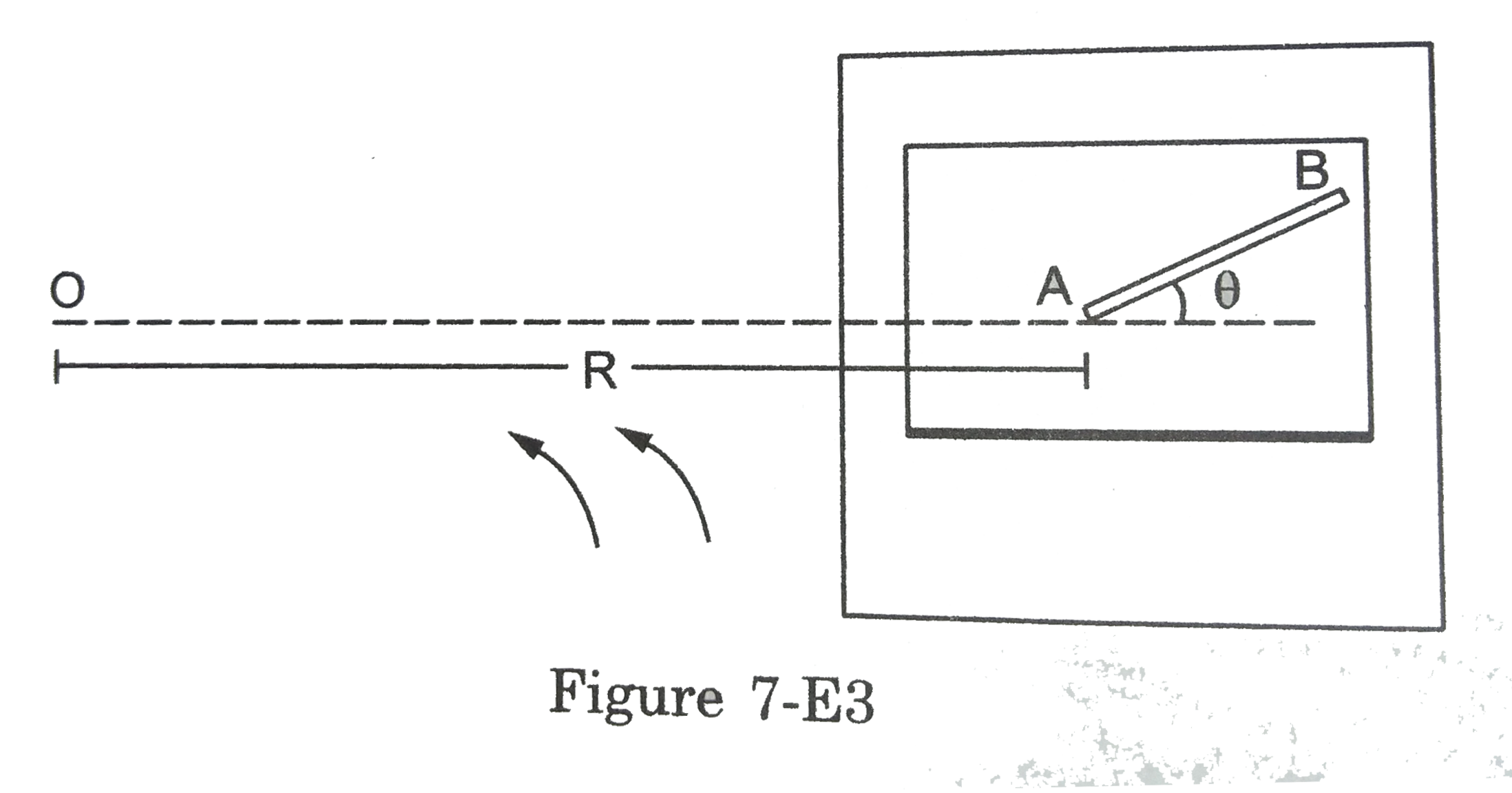 03:20View Solution
03:20View SolutionA child is swinging a ball of mass `M` around on a light spring which has spring constant `k`. The ball describes a horizontal circle. The stretched spring has a length a horizontal circle. The stretched spring has a length `l` and makes an angle `theta` with the vertical as shown in fig. the acceleration due to gravity is g neglect air resistance.
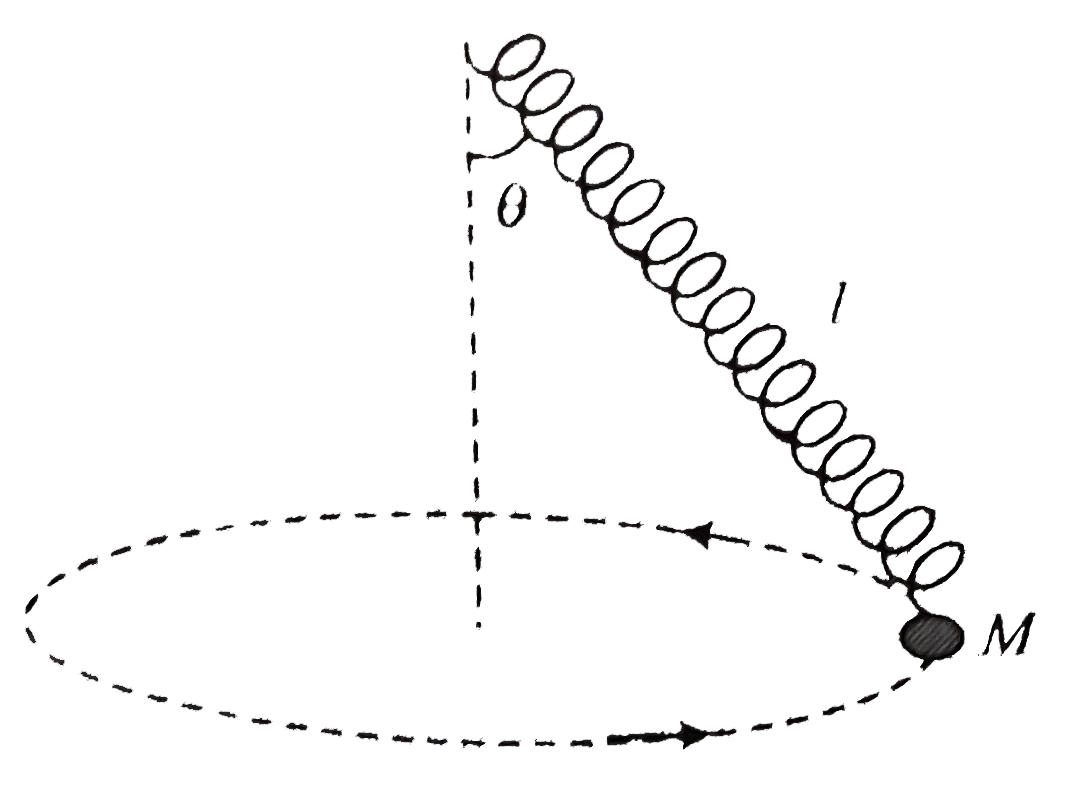
a. In terms of only the given quantities , what is the magnitude of force `F` that the spring exerts on man `M`?
b.In terms of `F,k`and `l`what is the natural length `l_(0)` of the spring i.e. the length of the spring when it is not steched?
c. In terms of `F, l,M` and `B` what is the speed v of the ball?04:36View Solution
Exercise 7.3 questions and complete solutions for chapter NEWTON'S LAWS OF MOTION 2 of CENGAGE PHYSICS (HINGLISH) of Class 11
