Complete Solutions to Single Correct of chapter NEWTON'S LAWS OF MOTION 2 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTON'S LAWS OF MOTION 2 |
| CENGAGE PHYSICS | Single Correct |
| Number Of Questions | 87 |
| Academic Year | 2023-24 |
Two block of masses `M_(1)` and, `M_(2)` are connected with a string which passed over a smooth pulley . The mass `M_(1)` is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is `mu` what should be the minimum mass `M_(2)` so that the block `M_(1)` slides upwards?
 02:35View Solution
02:35View SolutionA box of mass `8 kg ` placed on a rough inclined plane of inclened `theta` its downward motion can be prevented by applying an upward pull `F` and it can be made to slide upward appliying a force `2F` .The coefficient of friction between the box and the inclined plane is
02:40View SolutionA block of mass `15 kg` is resting on a rough inclined plane as shown in figure ,The block is tied by a horizontal string which has a tension `50 N` The coefficient of contact is
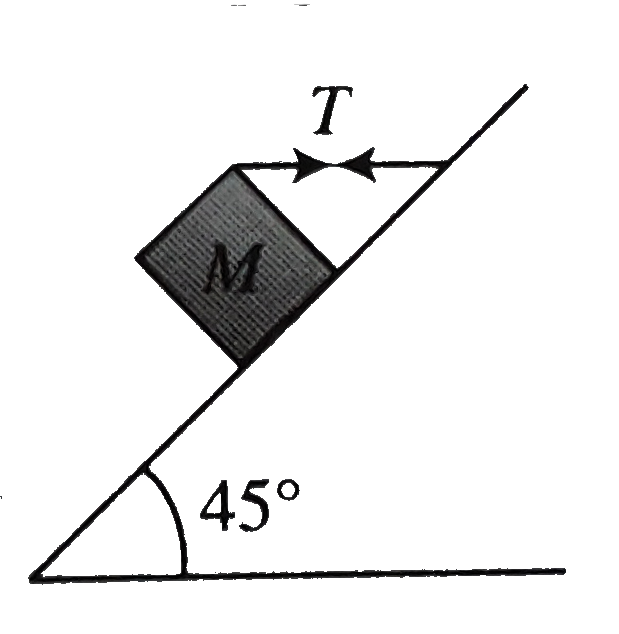 03:29View Solution
03:29View SolutionA horizontal force just sufficient to move a body of mass `4 kg ` lying on a rought horizontal surface is applied on it .The coefficient of static and kinetic friction the body and the surface are `0.8 and 0.6` respectively If the force contines to act even after the block has started moving the acceleration of the block in `ms^(-2)` is `(g = 10 ms^(-2))`
02:36View SolutionBlocks A and B in the Fig are connected by a bar of negligible weight .Mass of each block is `170 kg` and `mu_(A) = 0.2` and `mu_(B) = 0.4` where `mu_(A)` and `mu_(B)`are the coefficient of limiting friction between bloock and plane calculate the force developed in the bar`(g = 10 ms^(-2))`
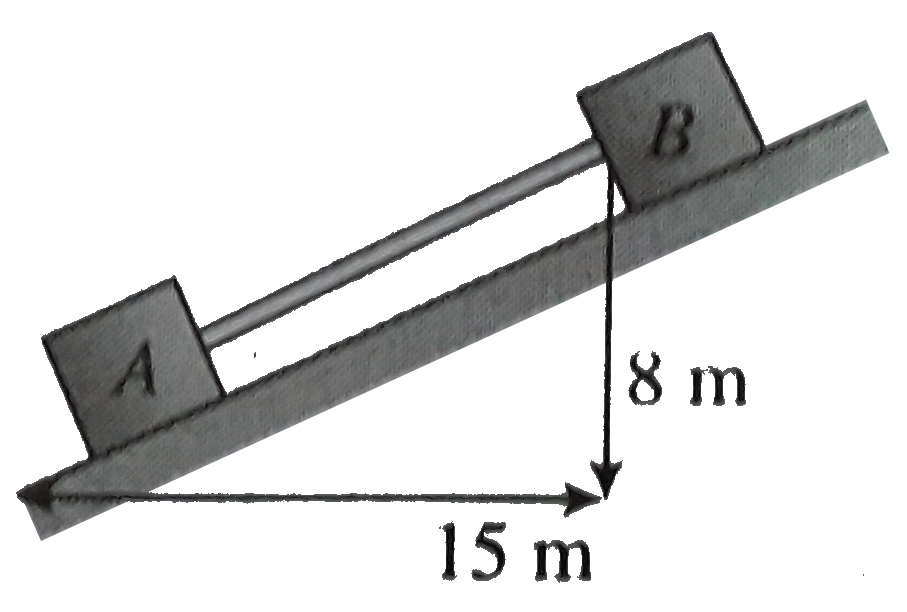 05:49View Solution
05:49View SolutionThe upper half of an inclined plane with inclination `phi` is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
05:20View SolutionA block of mass` m` is placed on another block of mass `M` which itself is lying on a horizontal surface .The coefficient of friction between two blocks is `mu_(1) `and that between the block of mass `M` and horizontal surfece is `mu_(2)` What maximum horizontal force can be applied to the lower block move without separation?
 02:52View Solution
02:52View SolutionTwo block A and B of masses `6 kg` and `3 kg ` rest on a smooth horizontal surface as shown in figure If coefficient of friction between A and Bb is `0.4` the maximum horizontal force which can make them move without separation is
 02:17View Solution
02:17View SolutionTwo block of masses `M_(1) and M_(2)` are connected with a string passing over a pulley as shown in figure The block `M_(1)` lies on a horizontal surface friction between the block `M_(1)` and the horizontal surface is `mu` The system accelerates. What additional mass `m` should be plased on the block `M_(1)` so that the system does not accelerate ?
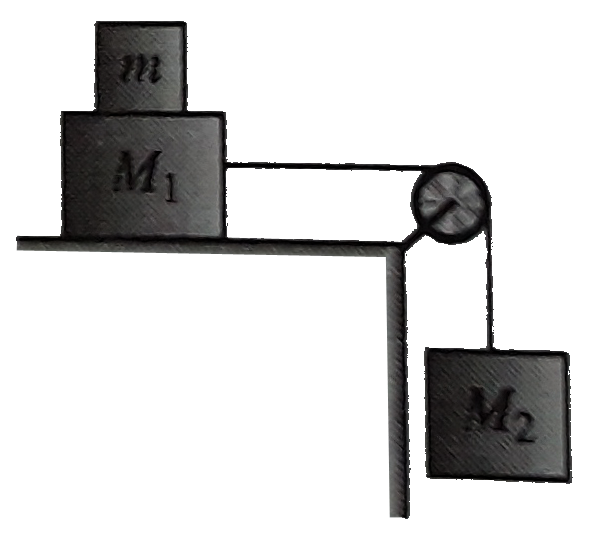 01:53View Solution
01:53View SolutionA system is pushed by a force `F` as shown in figure All surfaces are smooth except between `B` and `C` is `mu`. Minimum value of `F` to prevent block `B` from downward slipping is
 04:14View Solution
04:14View SolutionA body of mass `M` is resting on a rough horizontal plane surface the coefficient of friction being equal to `mu` At `t = 0` a horizontal force `F = F_(0) t` starts acting on it , where `F_(0)` is a constant find the time T at which the motion starts?
00:57View SolutionThe maximum value of mass of block C so that neither A nor B moves is (given that mass of A is `100 kg` and the of B `140 kg`. Pulleys are smooth and friction coefficient between A and B and horizontal surface `mu = 0.3)`(Taking` g = 10 ms^(-2))`
 05:15View Solution
05:15View SolutionA block A of mass `2 kg` is placed over smooth block B of mass `4 kg` which is placed over a smooth horizontal floor The coefficient of friction between A and B is `0.4` when a horizontal forces of magnitude `10 N` is applied on A the acceleration of block of A and B are
 05:26View Solution
05:26View SolutionTwo block `m and M` tied together with an inextensible string are placed at rest on a rought horizontal surface with coefficient of friction `mu` The block `m` is pulled with a variable force `F` at a varying angle `theta` with the horizontal .The value of `theta` at which the least value of `F` is required to move the blocks given by
 03:15View Solution
03:15View SolutionA trolley has a simple pendulum suspended from a frame fixed to itsa desk A block B is in contact on its vertical and The trolley is on horizontal rails and acceleration toward the right such that the block is just orevented from falling The value of coefficient of friction between A and B is `0.5` to the vertical is
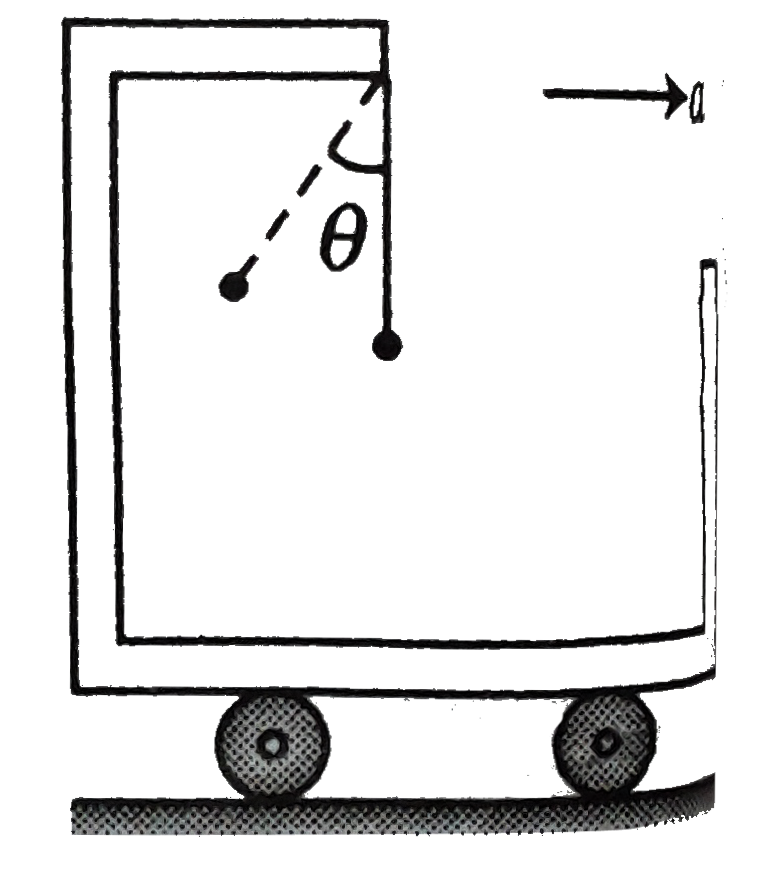 02:36View Solution
02:36View SolutionTwo blocks `M` and `m` are arranged as shown in the diagram The coefficient of friction between the block is `mu_(1) = 0.25` and between the ground and `M` is `mu_(2) = (1)/(3)` If `M = 8 kg` then find the value of `m` so that the system will remain at rest
 05:12View Solution
05:12View SolutionA body of mass `m` is launched up on a rough inclined plane making an angle `45^(@)` with horizontal If the time of descent between plane and body is
06:15View SolutionA block of mass `m` is placed at rest on a horizontal rough surface with angle of friction `phi`. The block is pulled with a force `F` at an angle `theta` with the horizontal. The minimum value of `F` required to move the block is
05:23View SolutionThe time taken by a body to slide down a rough `45^(@)` inclined plane is twice that required to slide down a smooth `45^(@)` inclined plane. The coefficient of kinetic friction between the object and rough plane is given by
05:12View SolutionA passenger is traveling a train moving at `40 ms^(-1)` Hit suitcase is kept on the berth ,The drive of train applies breaks such that the speed of the train decreases at a constant rate to `20 ms^(-1)` in `5s` What should be the minimum coefficient of friction between the suitcase and the berth if the suitcase is not to slide during and retardation of the train ?
03:29View SolutionIn figure the tension in the rope (rope is light) is
 02:26View Solution
02:26View SolutionAn inclined plane is moving up with constant velocity `v`. A block kept on incline is at rest. Calculate the work done by gravity, friction force, and normal reaciton on block in time interval of t.
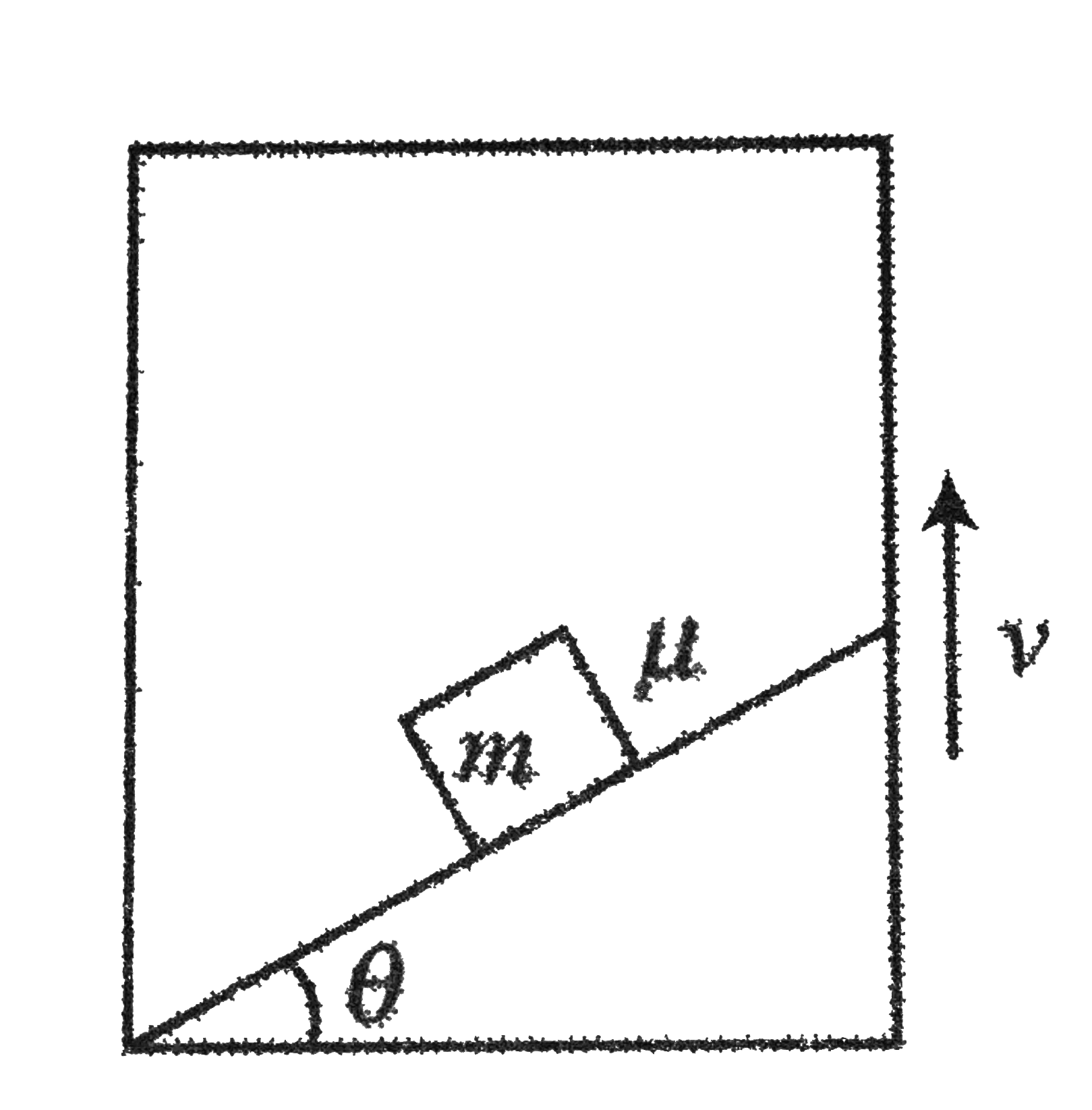 07:33View Solution
07:33View SolutionA block of mass `m` lying on a horizontal plane , is acted upon by a horizontal force p and another force `Q` inclined at an angle `theta` to the vertical .The block will remain in equilibrium if the coefficient of friction between it and the surface is (assume `p gt Q)`
 02:30View Solution
02:30View SolutionA horizontal force of `25 N` is necessary to just bold a block stationary against between the block and the wall is `0.4` The weight of the block is
 01:15View Solution
01:15View SolutionA solid block of mass `2 kg` is resting inside a cube shown in figure The cube is moving with a velocity `hatv= 5 hati + 2hatj ms^(-1)` If the coefficient of friction between the surface of cube and block is `0.2` then the force of friction between the block and cube is
 01:18View Solution
01:18View SolutionA block of mass `m` is lying on a wedge having inclination angle `alpha = tan^(-1)((1)/(5))` wedge is moving with a constant acceleration `a = 2 ms^(-2)` The minimum value of coefficient of friction `mu` so that `m` remain stationary w.r.t. wedge is
 04:56View Solution
04:56View SolutionIn Fig the block are at rest a force of `10 N` act on the block of `4 kg` mass .The coefficient of staic friction and the coefficient of kinetic friction are `mu_(s) = 0.2 and mu_(s) = 0.15` for both the surface in contact The magnitudeof frcition force acting between the surface of contact between the `2 kg` and `4 kg` block in this situation is
 03:10View Solution
03:10View SolutionThe masses of the block A and B are `m and M` Between A and B there is a constant force `F` but B can slide frictionlessly on the horizontal surface A is set in motion with velocity `v_(0)` while B is at rest . What is the distance moved by A relative to B before they move with the same velocity
 04:21View Solution
04:21View SolutionThere block A B ,and C of equal mass `m` are placed one over the other on a frictionless surface (table) as shown in figure The coefficient of friction between any blocks A ,B and C is `mu` The maximum value of mass of block D so that the blocks A,B and C move without slipping over each other is
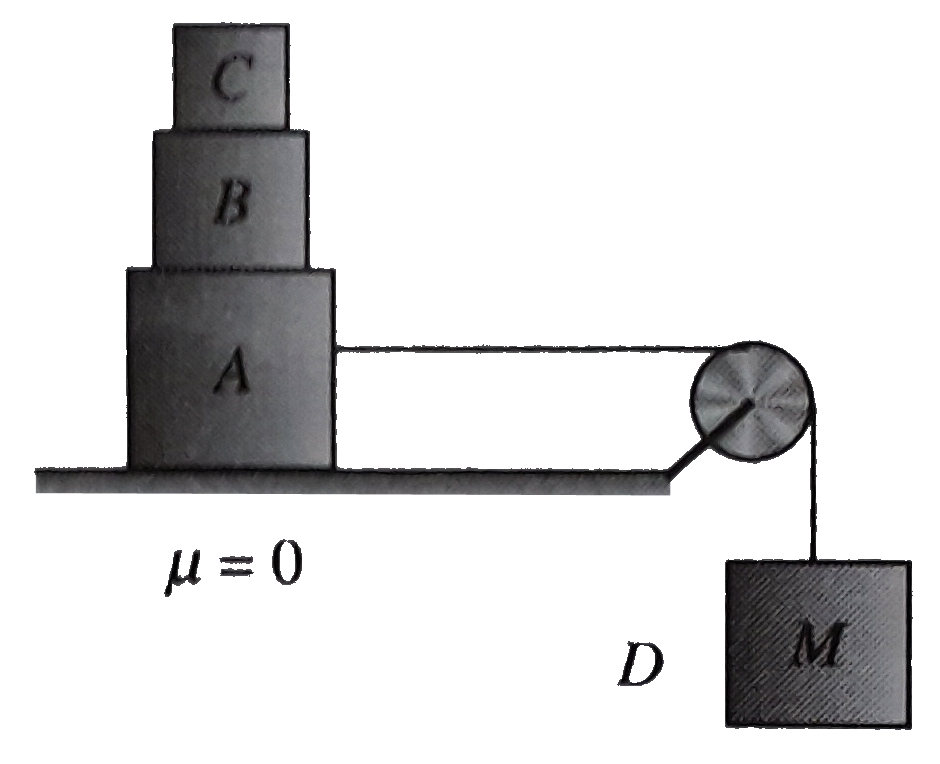 02:44View Solution
02:44View SolutionTwo blocks of masses of `0.2 kg` and `0.5 kg` which are placed `22m` apart on a horizontal surface `(mu = 0.5)` are acted upon by two forces of magnitude `3 N` each as shown in figure in time `t = 0` Then the time t at which they collide with each other is
 03:48View Solution
03:48View SolutionA chain of length L is placed on a horizontal surface as shown in figure. At any instant x is the length of chain on rough surface and the remaining portion lies on smooth surface. Initially ` x= 0`. A horizontal force p is applied to the chain (as shown in figure) in the duration from `x = 0 to x = L`. For chain to move with constant speed
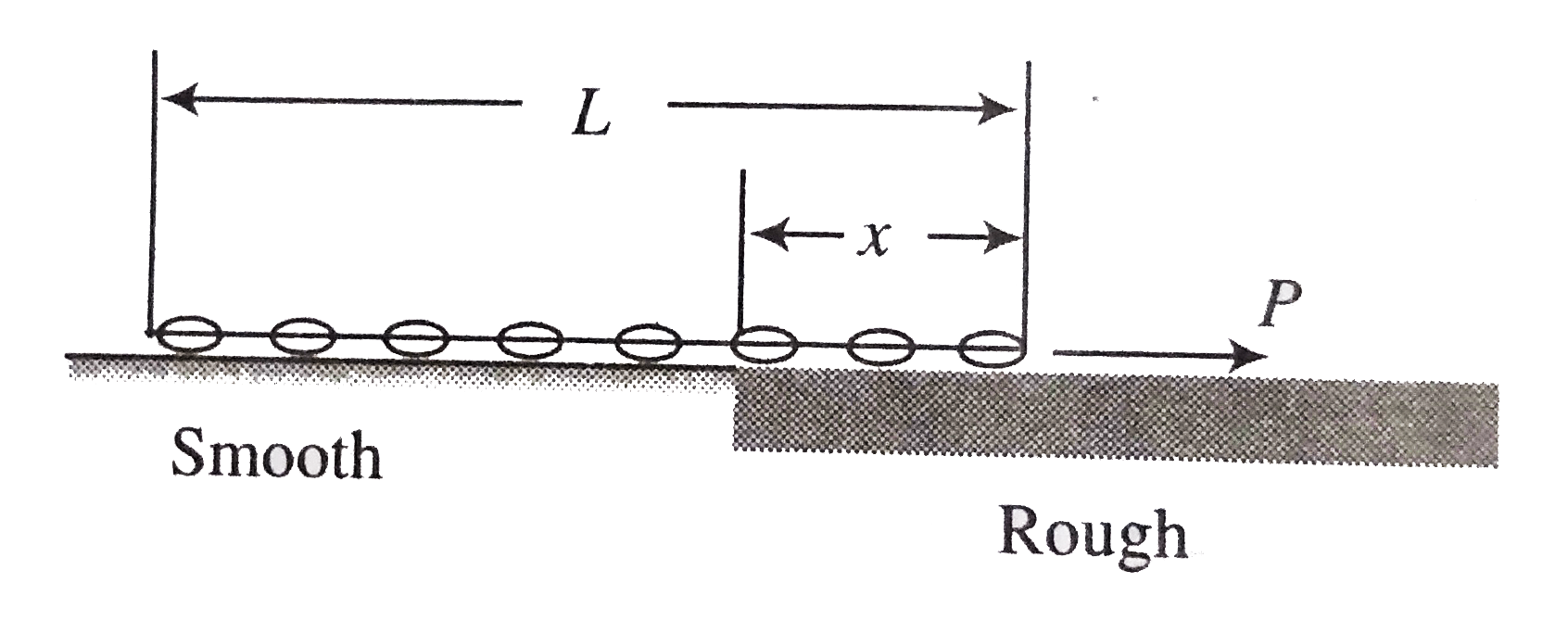 02:29View Solution
02:29View SolutionA vehicle in moving with a velocity v on a carved total of width b and radius of curvature B For counteractiong the contritugal force on the vehicle , the difference in elevation required in between the outer and linner edges of the rod is
 03:01View Solution
03:01View SolutionA circular road of radius `1000m` has hanging angle `45^(@)` The maximum safe speed (in `ms^(-1)` of a car having a mass `2000kg ` will be (if the coefficient of friction between tying and road is `0.3)`
01:46View SolutionA circular table of radius `0.5 m` has a smooth diametrical groove. A half of mass `90g` is is placed inside the groove along with a spring constant `10^(2)N cm^(-1)` One end of the spring is tied to the table and the other end to the ball The ball is at a distance of `.0.1 m` from the center when the table is at rest On rotating the table with a constant angular frequency of `10^(2)(rad)/s^(-1)` the ball moves away from the center by a distance nearly equal to
03:38View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is `mu_(s)` .Find the velocity of the before it start sliding relative as the disc
 02:40View Solution
02:40View SolutionA house is built on the top of a hill with `45^(@)`slope Due to the sliding of meterial and sand top from top to the bottom of till , the slip angle has been redaced if the coefficient of static friction between sand particles is `0.75` what is the final angle attated by bill ? `(tan^(-1) 0.75= 37^(@))`
 02:54View Solution
02:54View SolutionA block of mass `4 kg` is pressed againest the wall by a force of `80N` as shown in figure Determine the value of the friction force and block's acceleration (Take `mu_(s) = 0.2 , mu_(s) = 0.15)`
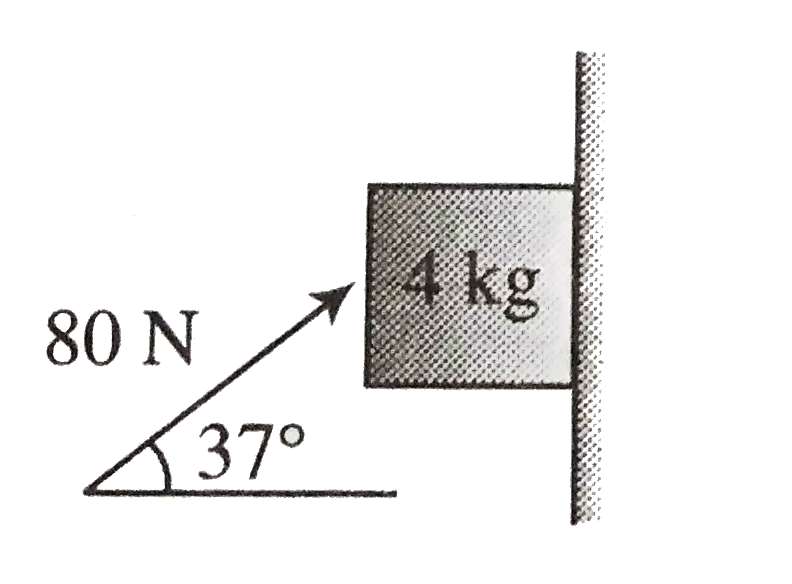 01:54View Solution
01:54View SolutionFor the situation shown in Fig the block is sationary w.r.t.inclined fixed in an elevator the alevator is having an acceleration of `sqrt(5)a_(0)` whose components are shown in the figure the surface is rought and coefficient of static friction between the inclined and block is `mu` Determine the magnitude of force excerted by inclined on the block (Take` a_(0) = g//2 and theta = 37^(@) , mu_(s) = 0.2)`
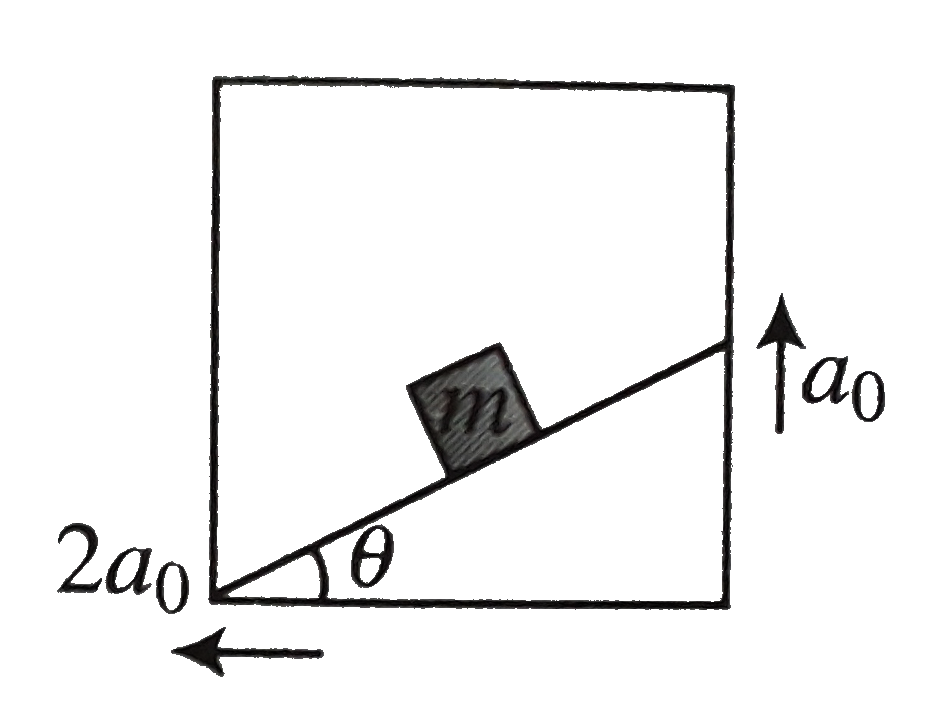 07:02View Solution
07:02View SolutionIf the coefficient of friction between all surface figure is `0.4` then find the minimum force `F` to have equilibrium of the system.
 07:16View Solution
07:16View SolutionFind the least horizontal force P to start motion of any part of the system of the three blocks resting upon one another as shown in figure The weights of blocks are `A = 300 N , B = 100 N` and `C = 200 N` .Between A and B , the coefficient of friction is `0.3` between B and C is `0.2` and between C and the ground is `0.1`
 02:42View Solution
02:42View SolutionA block of mass `m` attached with a massless spring of force constant k The block is placed over a rought inclined surface for which the coefficient of friction is `0.5M` is released from rest when the spring was unstretched The minimum to move the value of `M` required to move the block `m` up the plane is (neglect mass of spring and pulley and friction in pulley)
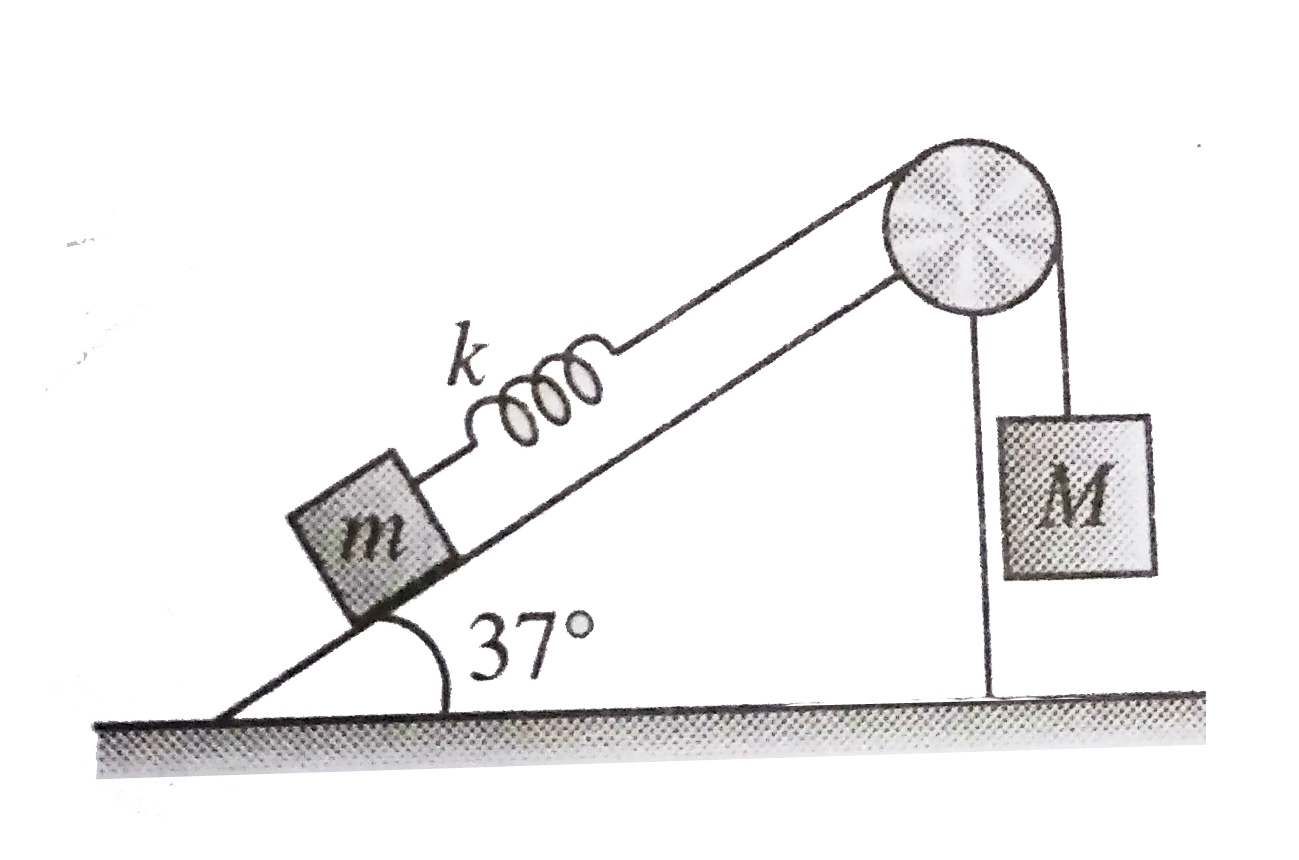 05:42View Solution
05:42View SolutionIn the system shown in Fig the friction coefficient between ground and bigger block is `mu` There is no friction between both the block .The string connecting both the block is light all three pulley are light and frictionless Then the minimum limiting value of `mu` so that the system remain in equilibrium , is
 02:50View Solution
02:50View SolutionTwo block A of `6 kg` and B of `4 kg` are placed in contact with each other as shown in figure
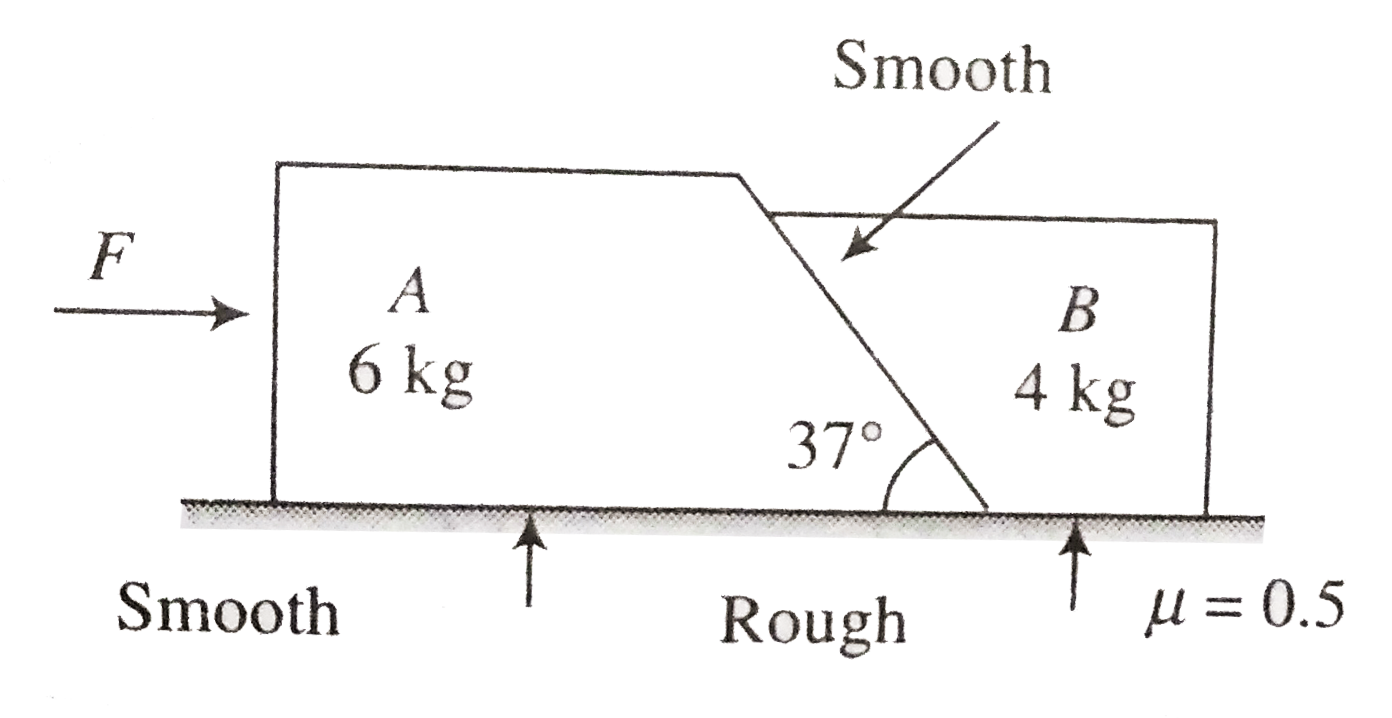
There is no friction A and ground and between both the blocks .The coefficient of friction between B and ground is `0.5` A horizontal force `F` is applied on A find the minimum and maximum value of `F` which can be applied so that both blocks can move combinely without any relative between them.08:55View SolutionTwo blocks of masses `3 kg` and `2 kg` are placed side by side on an inclined as shown in figuire A force `F = 292 A` force `F = 20N` is active on `2 kg` block along the inclined .The coefficient of friction between the block and the inclined is same and equal to `0.1` .Find the normal force exerted by `2 kg` block on `3 kg`block
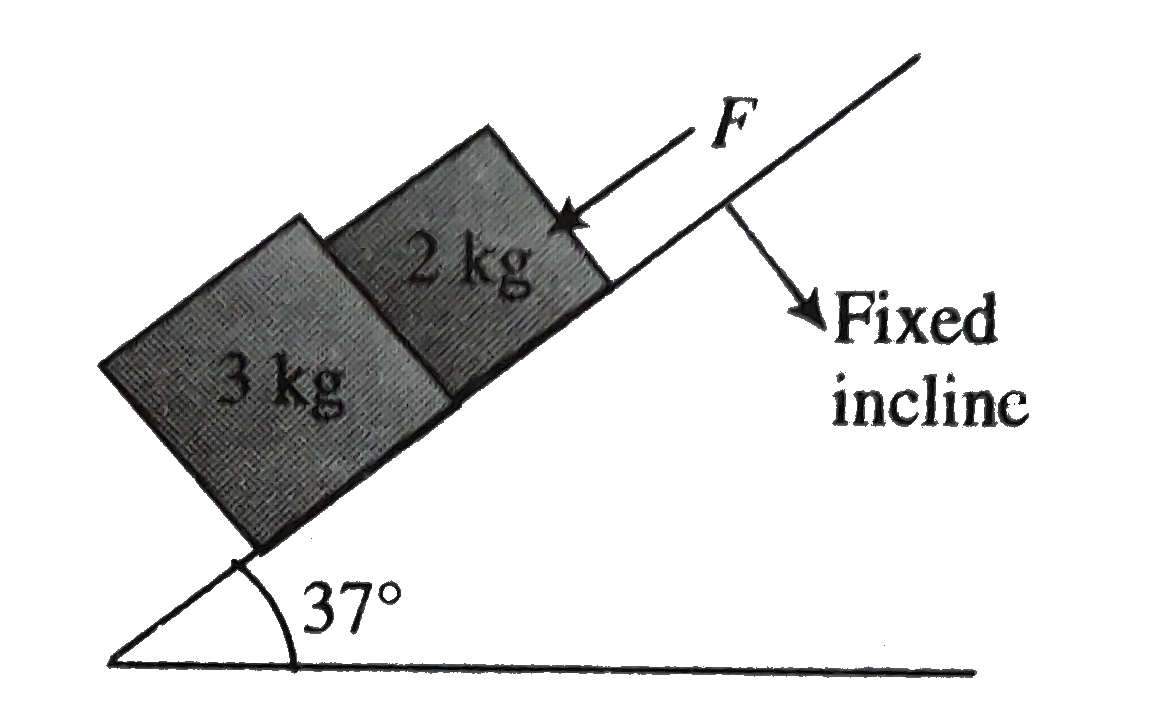 04:48View Solution
04:48View SolutionDetermine the time in which the smaller block reaches other end of bigger block in figure
 03:57View Solution
03:57View SolutionA uniform chain is placed at rest on a rought surface of base length 1 and height h on an irregular suface as shown in figure Then the minimum coefficient of friction between the chain and the surface must be equal to
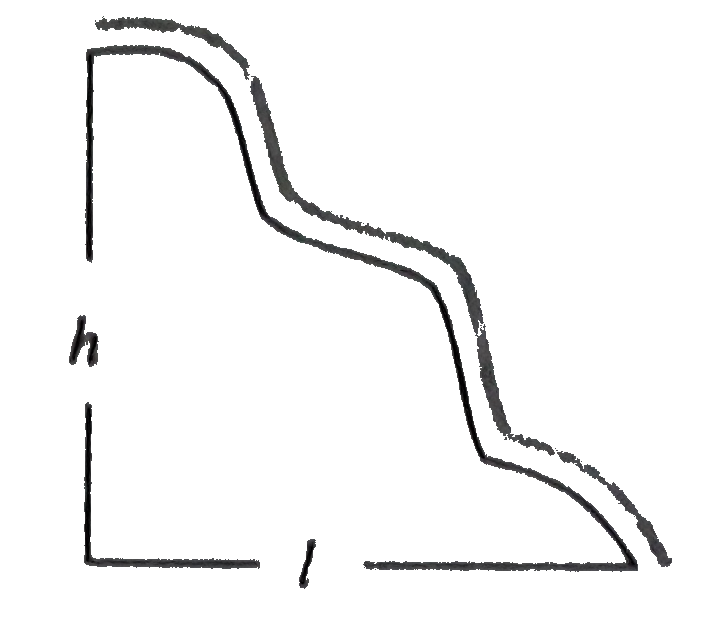 02:44View Solution
02:44View SolutionA block of mass `m` is at rest on a rough wedge as shown in figure. What is the force exerted by the wedge on the block?
 04:41View Solution
04:41View SolutionA triangular prism of mass `m` placed on it is released from rest on a smooth inclined plane of inclination `theta` The block does not slip on the prism. Then
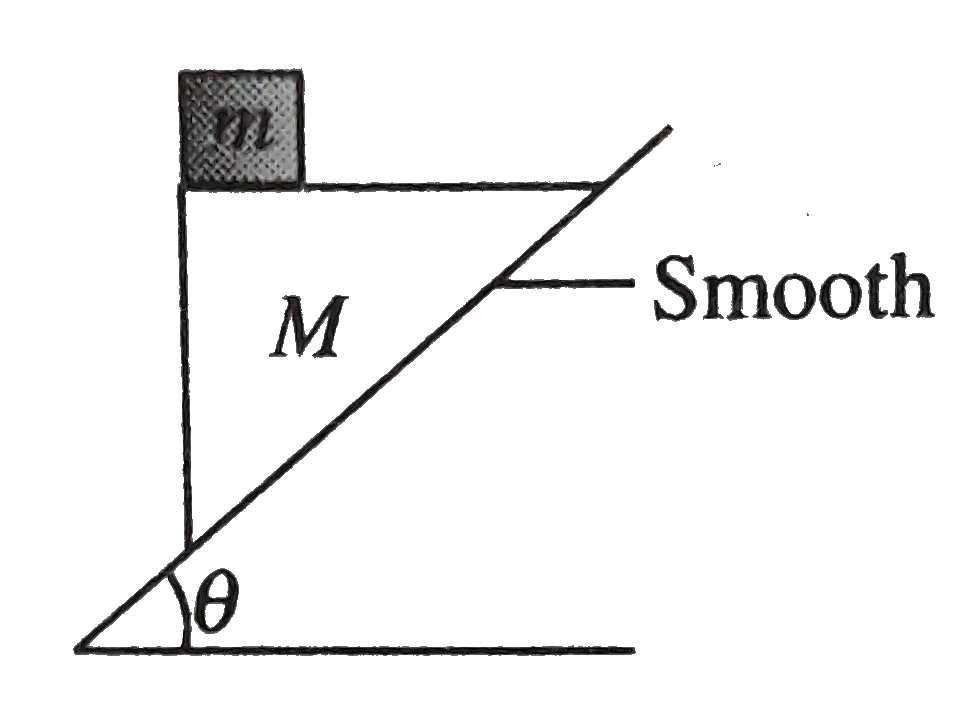 04:44View Solution
04:44View SolutionA block of mass `m` is kept on the floor of a freely falling lift .During the free fall of the lift, the block is pulled horizontally with a force of `F = 5 N, mu_(s) = 0.1`The friction force on the block will be
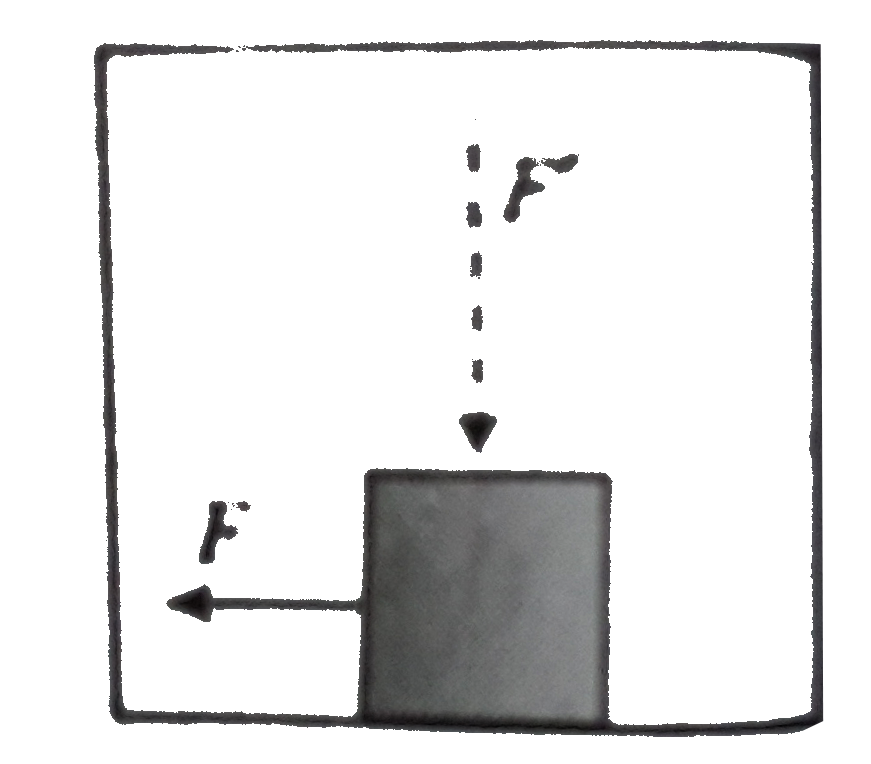 02:26View Solution
02:26View SolutionIf in pervious problem, an additional force `F' = 100N` is applied in vertical direction as shown in figure The friction force acting on the block is
04:10View SolutionA rectangular wooden box `10 cm xx 20cm xx 40 cm` is size is kept on a horizontal surface with its of lergest are on the surface .A minimum force of `10 N` applied are on the surface sets the box in sliding motion along the surface If the surface, minimum force applied parallel to the surface , to set the box in motion , is
03:12View SolutionTwo blocks `(m and M)` are arranged as in figure Then is friction between ground and `M` only and other surface are frictionless between ground and `M is mu = 0.25` The maximum ratio of `m` and `M(m//M)` so that the system remain is at rest
 02:45View Solution
02:45View SolutionIn the pulley arrangement shown in Fig the pulley `p_(2)` is movable .Assuming the coefficient of friction between `m` and surface to be `mu` the minimum value of `M` for which `m` is at rest is
 02:55View Solution
02:55View SolutionIn the arrangement shown in Fig there is no friction between of mass `2m` and ground but there is friction between the block of masses `m` is stationary with respect to block of mass `2m` The value of friction between `m` and `2m`is
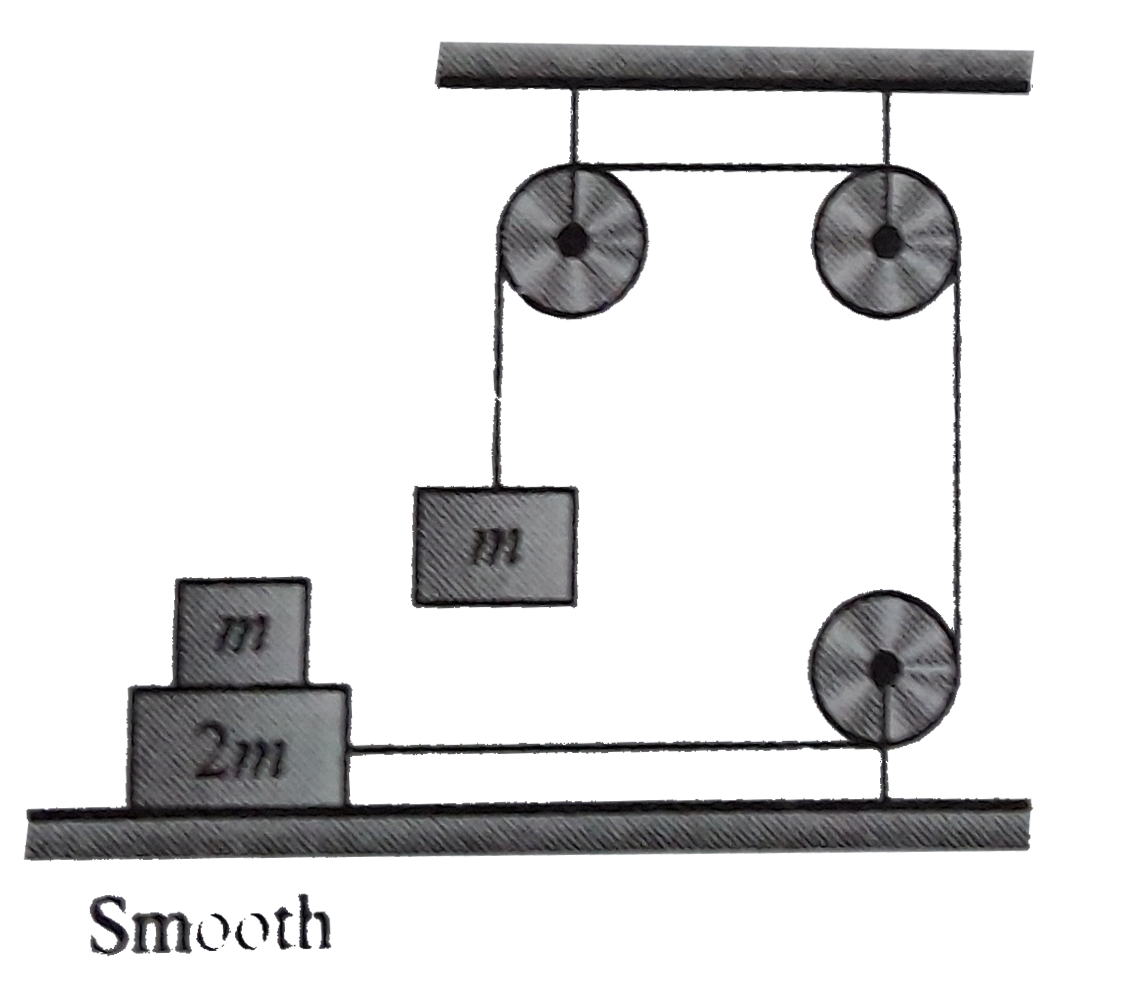 01:59View Solution
01:59View SolutionA lift moving with a uniform velocity v in which a block of mass `m` is lying .The friction force offered by the when coefficient of friction is `mu = 0.5` will be
01:21View SolutionA block of mass is kept on an inclined plane of a lift moving down with acceleration of `2 ms^(-2)` What should be the minimum coefficient of friction to let the block move down with constant velocity?
 03:47View Solution
03:47View SolutionThe system is pushed by a force F as shown in figure All surface are smooth except between B and C friction coefficient between B and C is Minimum value of F to prevent block B from down ward slipping is
 02:41View Solution
02:41View SolutionIf is problem - `57` all situation are same expect force is applied on block C as shown in figure in case (b) Minimum value of F to prevent block B from downward slipping is
04:14View SolutionA block of mass `M` is being pulley along horizontal surface .The coefficient of friction the block and the surface is `mu` If another block of mass `M//2` is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
03:40View SolutionBlock A as shown in Fig weighs `2.0 N` and block B weighs `6.0 N` The coefficient of ikinetic friction between all surface is `0.25` Find the magnitude of the horizontal force necessary to drag block B to the left at constant speed if A and B are connected by a light , flxeible cord passing around a fixed, frictionless pulley
 03:51View Solution
03:51View SolutionFigure shown a wooden block at rest in equilibrium on a rought horizontal plane being acted upon by force `F_(1) = 10 N, F_(2) = 2 N`, as shown .IF`F_(1)` is removed , the resulting force acting on the block will be
 02:10View Solution
02:10View SolutionA block of mass 2 kg is pushed against a rough vertical wall with a force os 40 N. Coefficient of static friction being 0.5. Another horizontal force is 15 N, is applied on the block in a direction paralle to the wall. Will the block move? If yes in which direction? If no, find the frictional force exerted by the wall on the block.
07:15View SolutionA main revolves a stone of mass `m` tied to the end of a string in a circle of radius R The net force at the lowest and height point of the circle directed vertical downward are
Here `T_(1),T_(2)` and `(v_(1),v_(2))` denote the tension in the string (and the speed of the stone) at the lowest and highest points, respectively.03:08View SolutionA ring of radius `r` is rotating about a vertical axis along its diameter with constant angular velocity `omega.A` read of mass `m` remains at rest `w.r.t.` ring at the position shown in figure. Then `w^(2)` is:
_2019_CBT8_E01_015_Q01.png) 04:25View Solution
04:25View SolutionWhen the string of a conical pendulum makes an angle of `45^(@)` with the vertical , its time is `T_(1)` when the string makes an angle of `60^(@)` with the vertical , its time period is `T_(2)` then `T_(1)^(2) // T_(2)^(2)`is
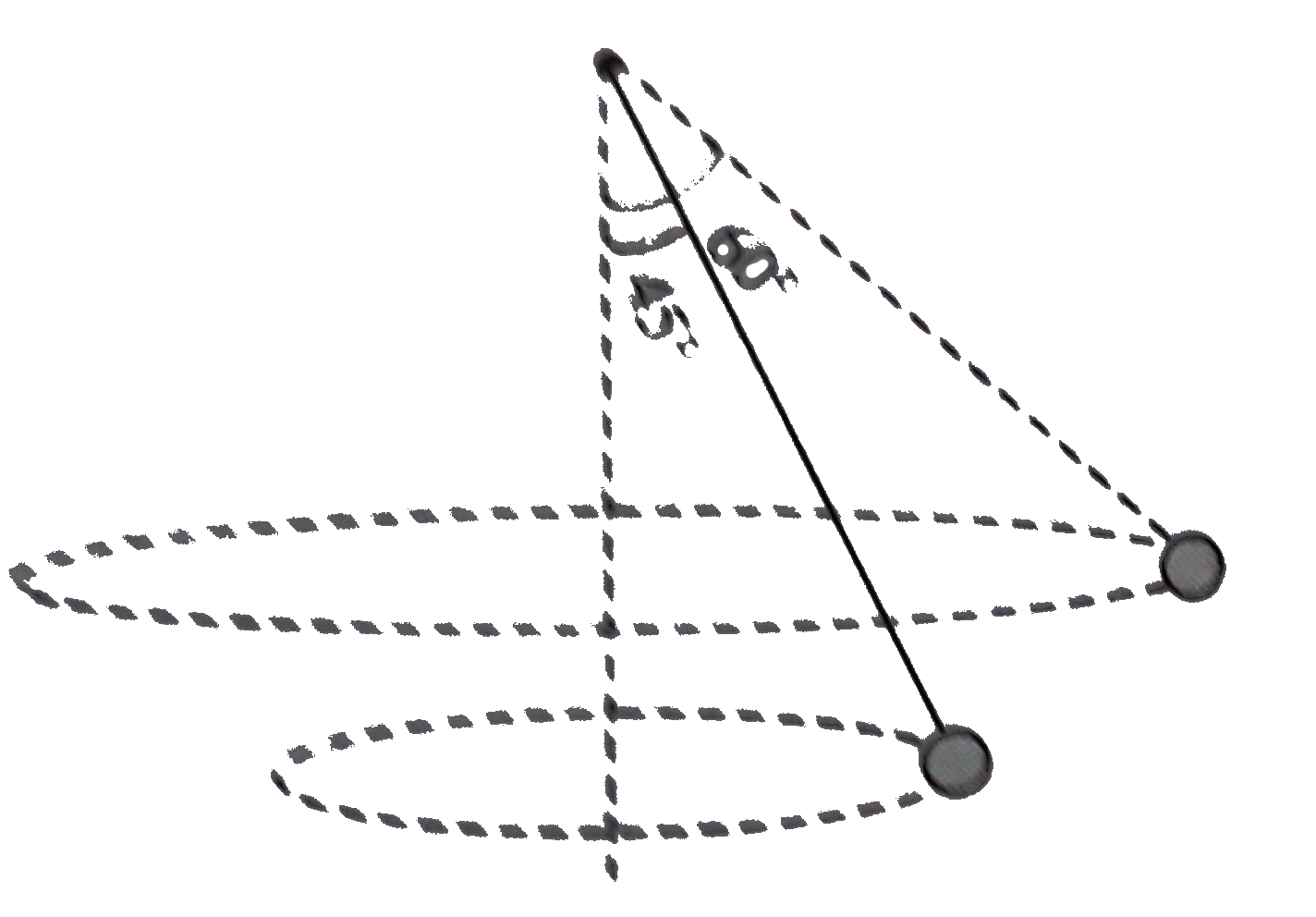 05:08View Solution
05:08View SolutionThree identical particles are joined together by a thread as shown in figure All the partical are moving in a horizontal plane If the vertical of the outermost particle is `v_(0)` then the ratio of tension in the three sections of the string `(T_(1):T_(2):T_(3) = ?)` is
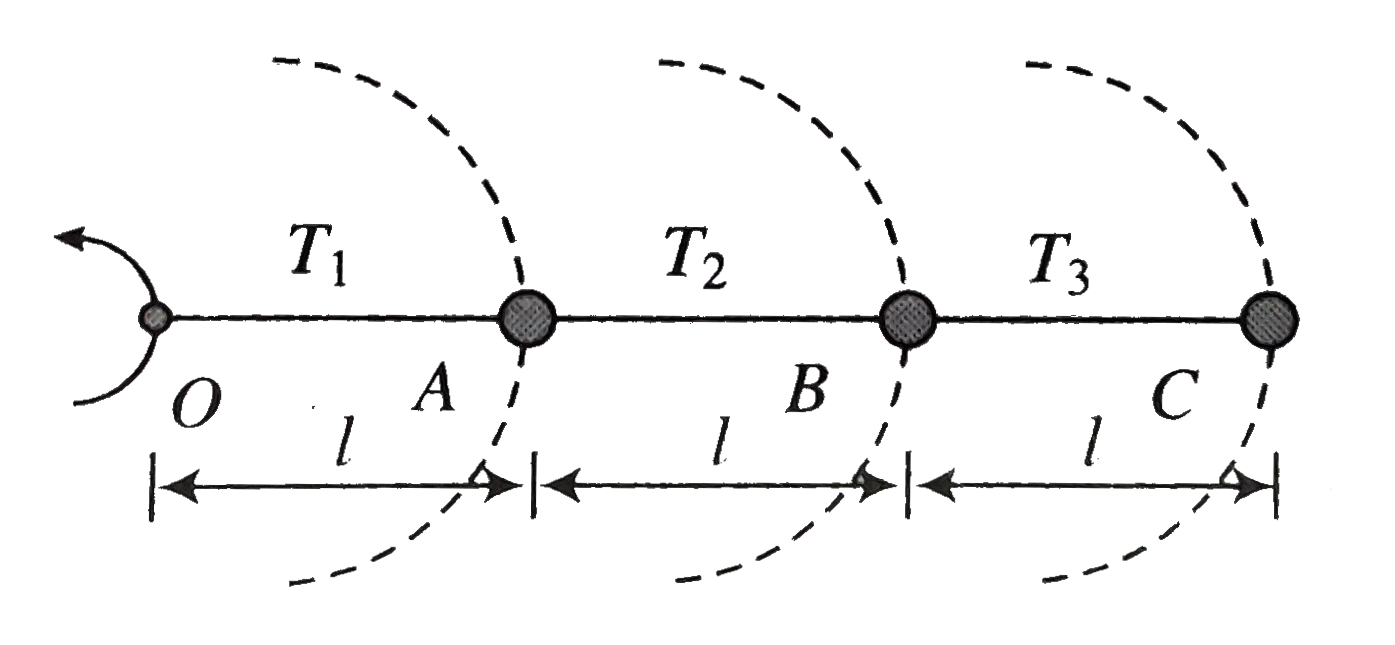 02:45View Solution
02:45View SolutionTwo identical particles are attached at the end of a light string which passes through a hole at the center of a table One of the partical is made to move in a circle on a table with angular velocity `omega_(1)` and the ther is made a move is a horizontal `omega_(2)` if `l_(1)`and `l_(2)` are the length the table , than in order that particle under down the table neither moves down nor move up the ratio` l_(1)//l_(2)` is
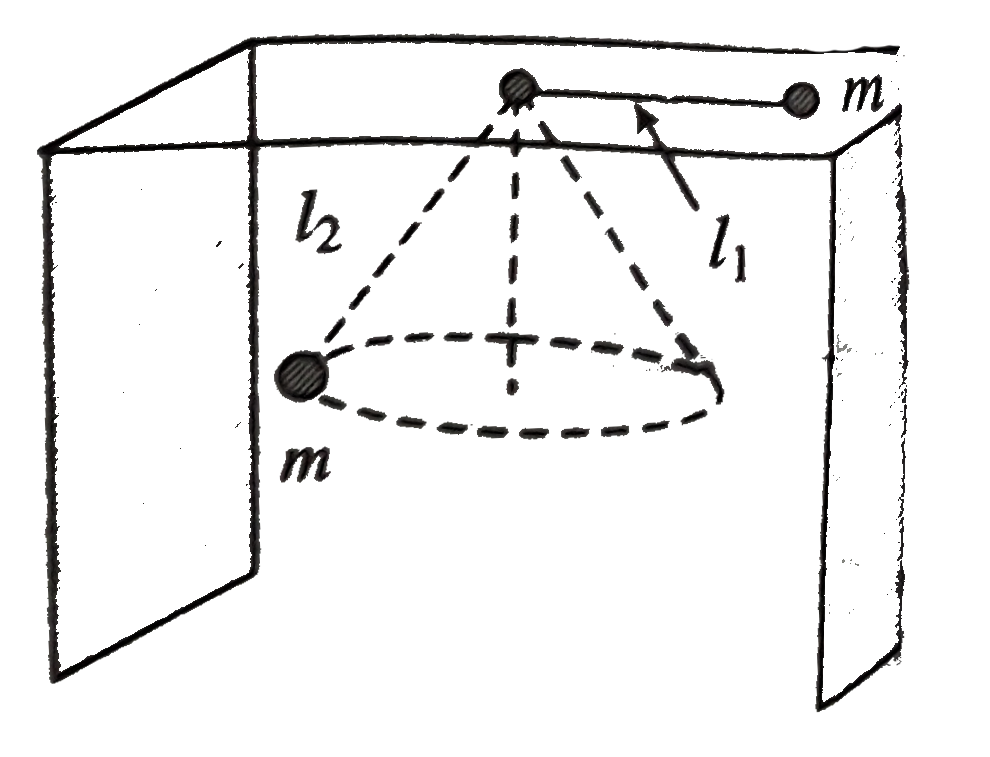 02:58View Solution
02:58View SolutionA block of mass `m` is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block
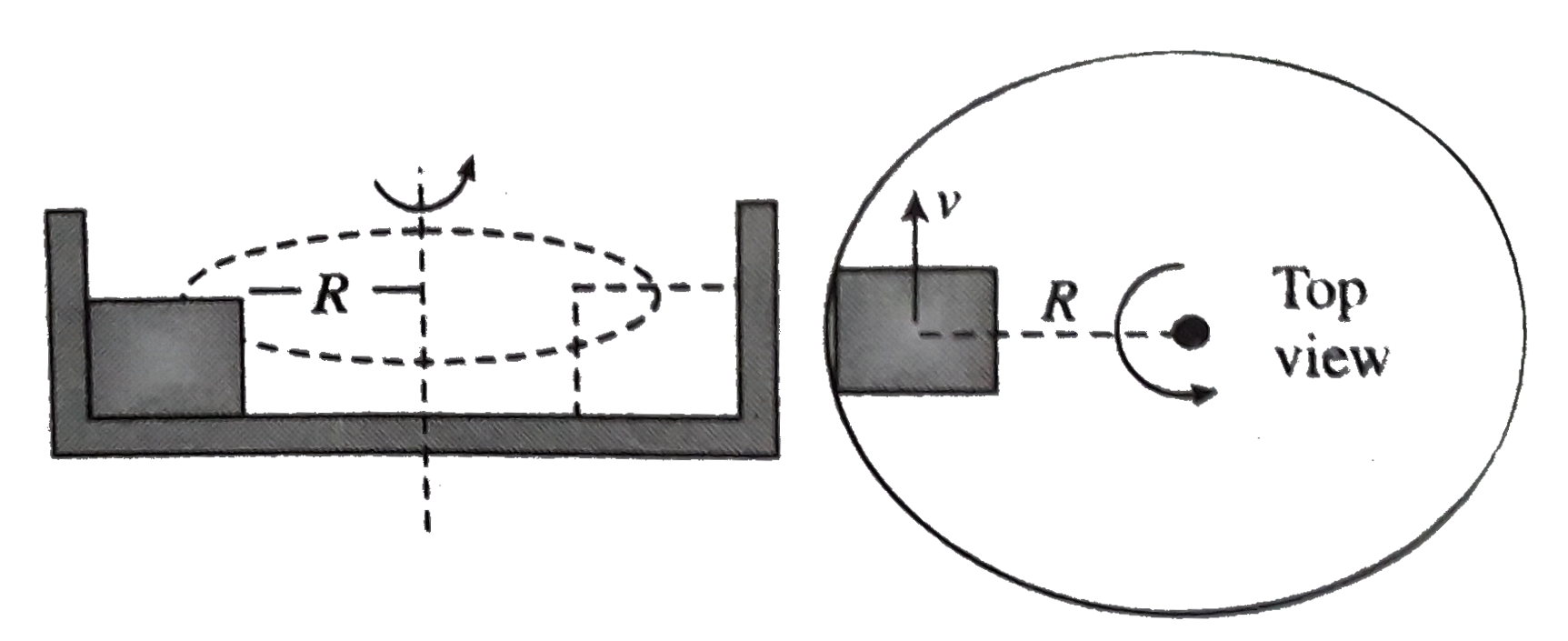 01:38View Solution
01:38View SolutionA particle is projected with a speed `v_(0) = sqrt(gR)`. The coefficient of friction the particle and the hemi- spherical plane is `mu = 0.5` Then , the acceleration of the partical is
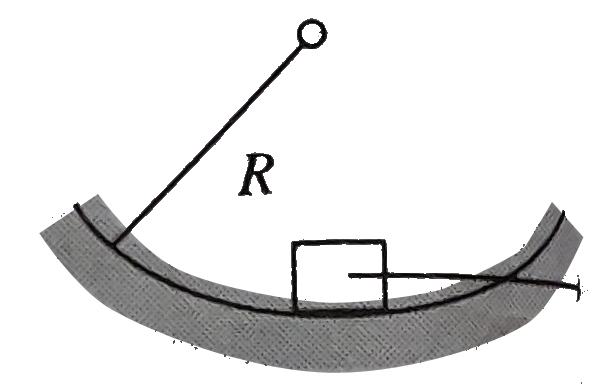 02:53View Solution
02:53View SolutionA car travels with constant speed on a circular road level ground in figure `F_(air)` is the force of air resistence acts opposite to the motion of car which of the other forces shown best represents the horizontal force of the road on the car's tires?
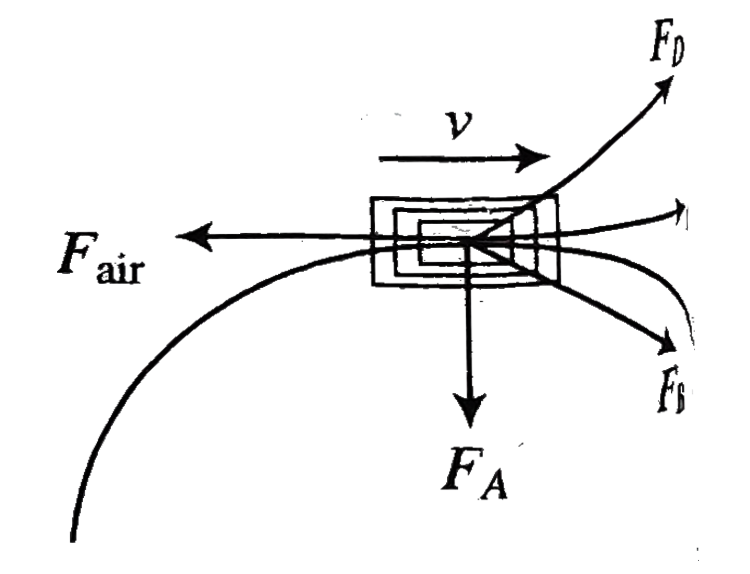 02:42View Solution
02:42View SolutionA block of mass `m` is projected on a smooth horizontal circular track with velocity v what is the average normal force exered by the circular walls on the block during motion A to B?
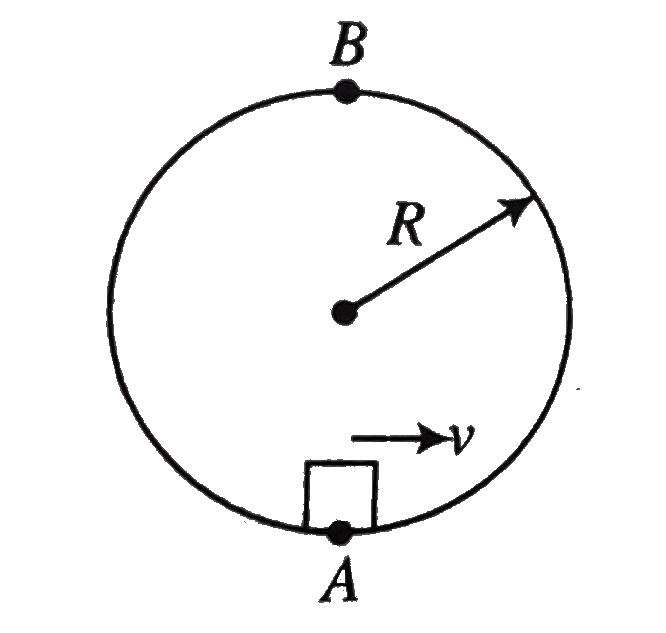 03:12View Solution
03:12View SolutionTwo cars A and B start racing at the same on a flat race track which consists of two strainght sections each of length `100 pi` and one circular section as shown in figure The rule of the race is that each car must travel at constant speed at all time without even skidding
 View Solution
View SolutionConsider the setup is of a Ferris wheel in an amusement part. The wheel is turning in acounterclockwise manner Contrary i.e. parralel to the x- axis Determine the orienation of the normal to seat as it passes point A
 01:59View Solution
01:59View SolutionTwo blocks of masses `m_(1)` and `m_(2)` are connected through a massless inextensible string .A block of mass `m_(1)` is placed at the fixed rigid inclined surface while the block of mass `m_(2)` hanging at the other end of the string which is passing through a fixed massless frictionless pulley shown in figure The coefficient of static friction between the block and the inclined plane is `0.8` The system of masses `m_(1)` and `m_(2)` released from rest
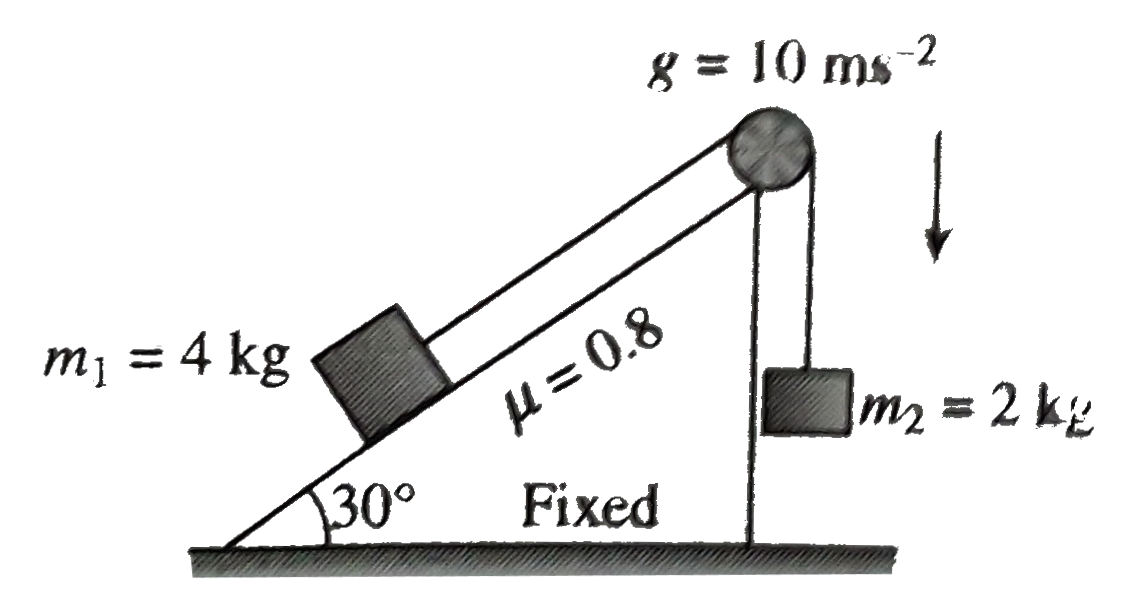 02:35View Solution
02:35View SolutionIn Fig if `F = 4N , m= 2 kg M = 4 kg` then
 03:15View Solution
03:15View SolutionA `20 kg` blocks is placed on of `50 kg `block as shown in figure An horizontal force `F` acting on A causes an acceleration of `3 ms^(-2)` to A and `2ms^(-2)` to B as shown in the figure for this situation mark out the corect statement(s)
 02:54View Solution
02:54View SolutionTwo blocks A and B of masses `m_(A)` and `m_(B)` have velocity v and `2v` respectively at a given instant A horizontal force F acts on the block A There is no friction between ground and block B and coefficient of friction between A and B is `mu` The friction
 01:16View Solution
01:16View SolutionTwo rough blocks A and B ,A placed over B move with acceleration `veca_(A)` and `veca_(B)` veclocities `vecv(A)` and `vecv_(B)` by the action of horizontal forces `vec(F_(A))` and `vec(F_(B))`, respectively. When no friction exsits between the blocks A and B,
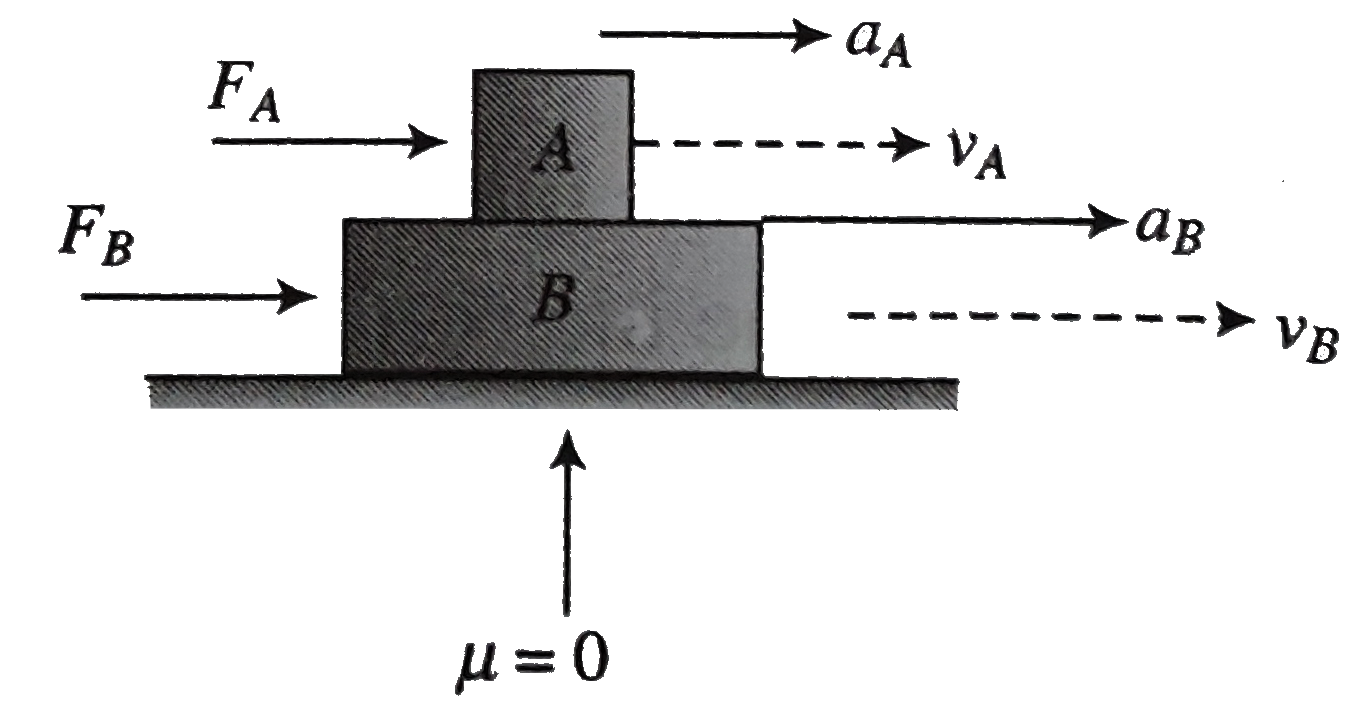 01:40View Solution
01:40View SolutionMark the correct statement (s) regarding friction .
02:54View SolutionA `3 kg` block of wood is on a level surface where `mu_(s) = 0.25` and `mu_(s) = 0.2 `A force of `7 N` is being applied horizontal to the block Mark the correct statement(s) regarding this situation.
02:59View SolutionA block is resting over a rough horizontal floor. At `t = 0` a time -verying force starts acting on it , the force is described by equation `F = kt` where k is constant and r is in seconds Marks the cerrect statement (s) for this situation .
 04:11View Solution
04:11View SolutionTwo blocks A and B of masses `5 kg` and `2 kg` respectively connected by a spring of force constant ` = 100Nm^(-1)` are placed on an inclined plane of inclined `30^(@)` as shown in figure If the system is released from rest
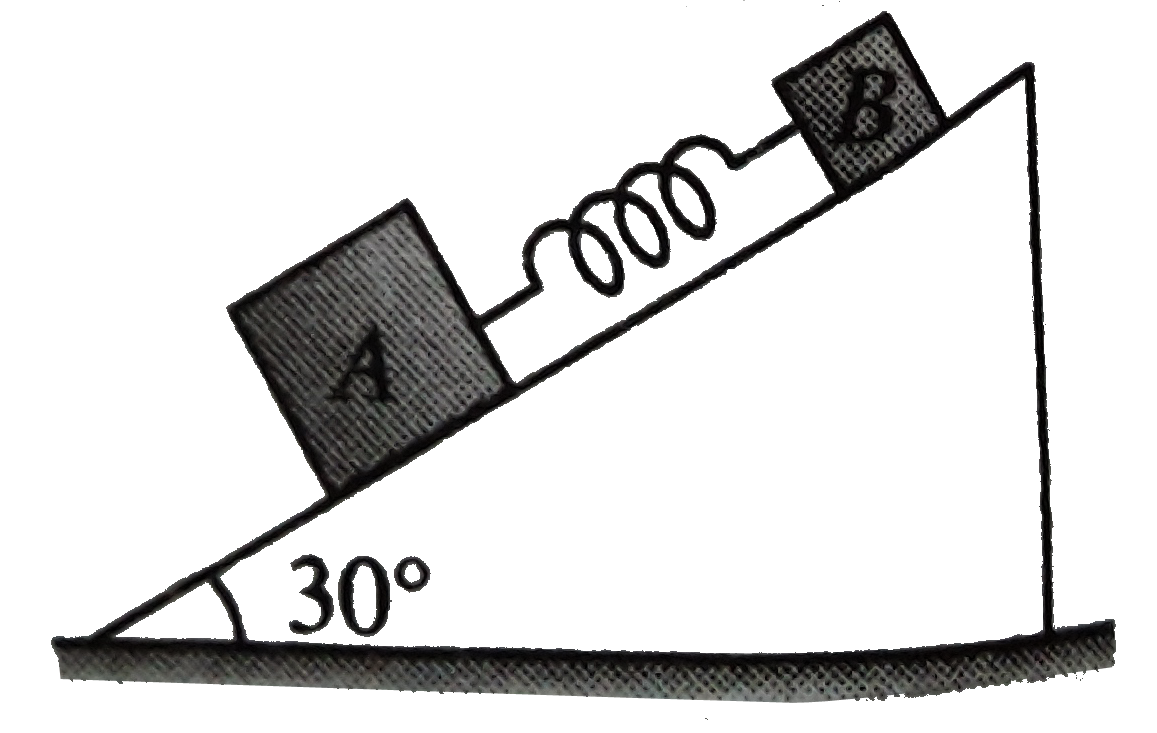 03:07View Solution
03:07View SolutionThe coefficient of friction between the two two blocks is `0.3` where as the surface AB is smooth
 04:49View Solution
04:49View SolutionA `10 kg` block is placed on top of a `40 kg` block as shown in figure .A horizontal force F acting on B cause an acceleration of `2 ms^(-2)` to B .For this situation marks our the correct statement(s)
 03:21View Solution
03:21View SolutionA car moving along a circular track of radius `50.0m` acceleration from rest at `3.00 ms^(2)` Consider a situation when the car's centripetal acceleration equal its tangential acceleration
03:51View SolutionA particle of `m_(1)` moves in a circular path of radius R on a rotating .A string connecting the particles `m_(1)` and `m_(2)` passes over a smooth bole made on the table as shown in figure If mass `m_(1)` does not slide relative to the rotating table , mark the correct option as applicable.
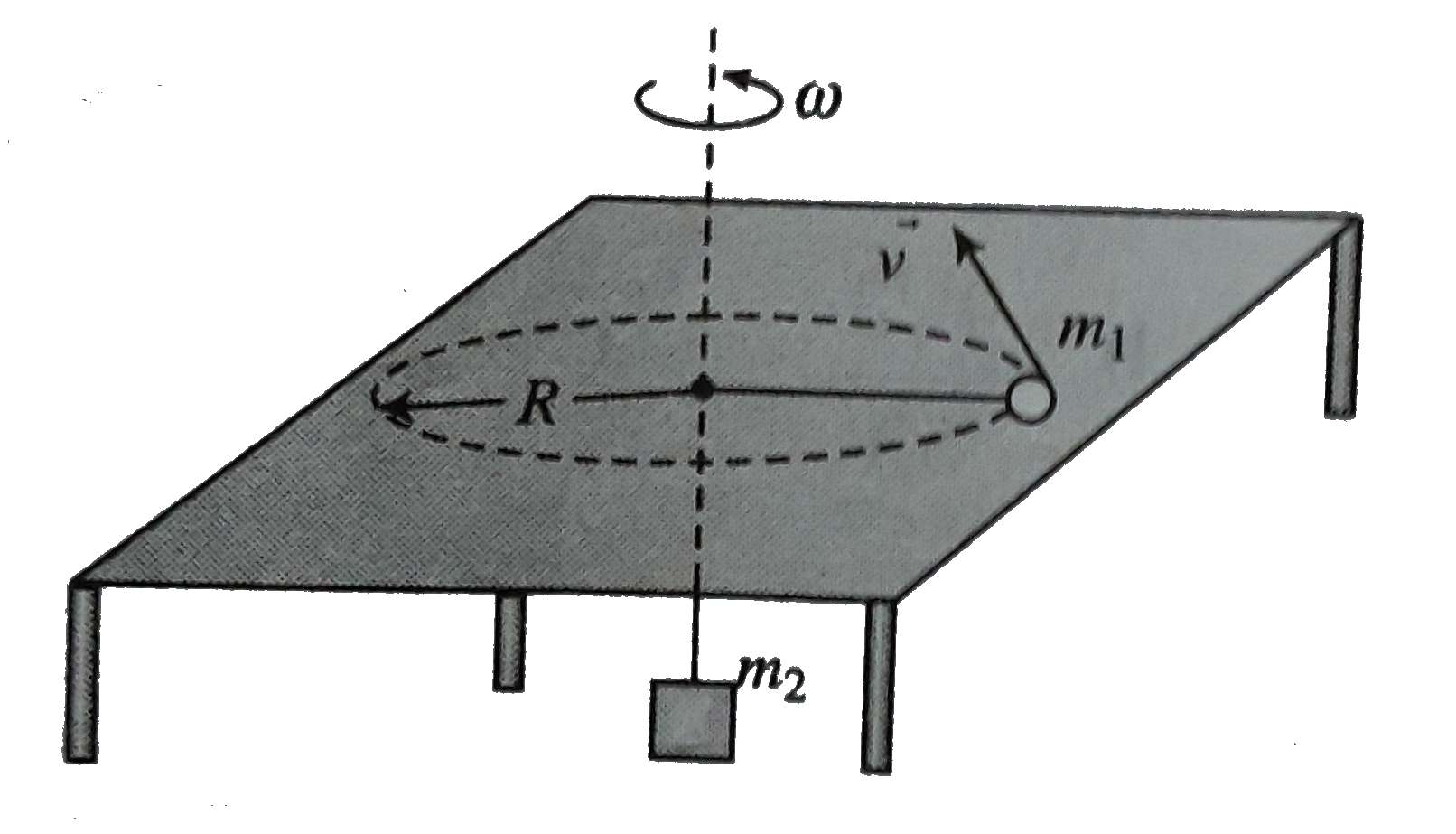 04:42View Solution
04:42View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is `mu = 0.4` where `F = 30 N` then

Acceleration of upper block is03:44View Solution
Single Correct questions and complete solutions for chapter NEWTON'S LAWS OF MOTION 2 of CENGAGE PHYSICS (HINGLISH) of Class 11
