Complete Solutions to Illustration of chapter NEWTON'S LAWS OF MOTION 2 of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTON'S LAWS OF MOTION 2 |
| CENGAGE PHYSICS | Illustration |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
A block of weight `100N` lying on a horizontal surface just beging to when a horizontal to move when a horinzontal force of `25 N` acts on it Determine the coefficent of static friction
01:49View SolutionIn Fig force `F` is gradually increased from zero Draw the graph between applied force `F` and tension `T` is the string . The coefficient of string friction between the block and the ground is `mu_(s)`
 03:15View Solution
03:15View SolutionFind the least pulling force which acting at an angle of `45^(@)` with the horizontal will slide a body weighing `5 kg` along a rough horizontal surface . The coefficient of friction `mu_(s) = mu_(k) = 1//3` If a force of doude this is applied along the same direction , find the resulting acceleration of the block
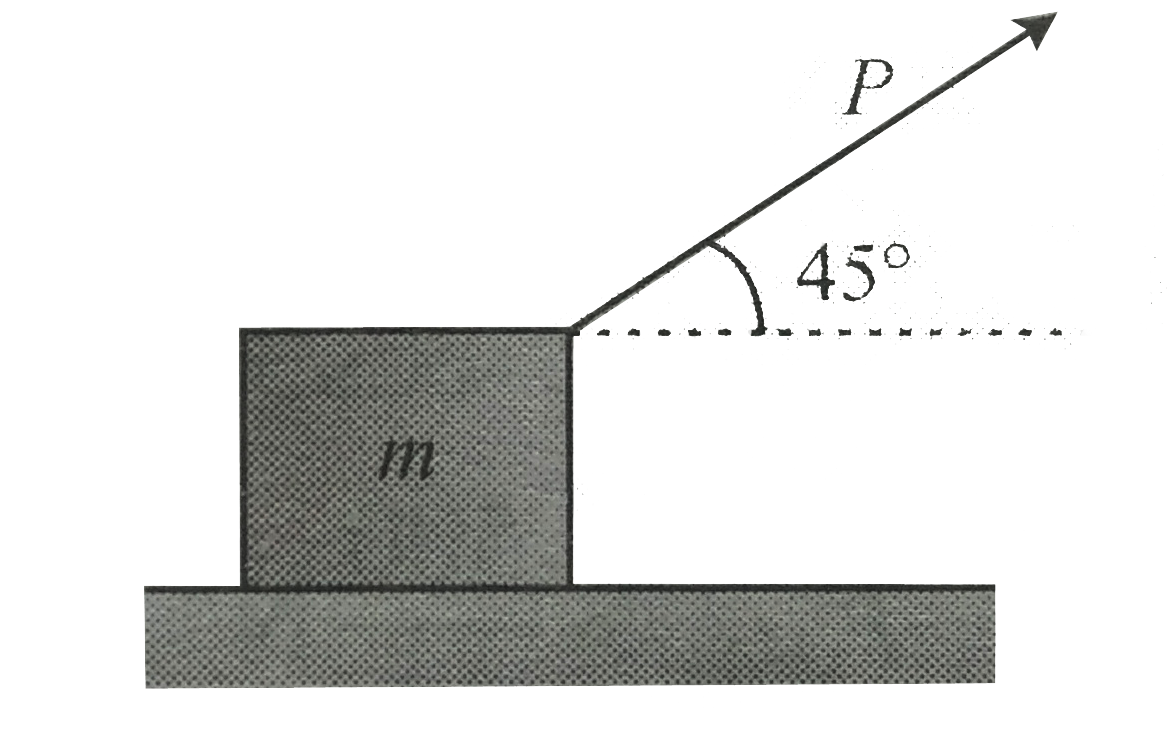 09:53View Solution
09:53View SolutionForce `F` is graduallly increased from zero .Determine whether the block will first slide or lift up?
 06:09View Solution
06:09View SolutionIn Figure an object of mass `M = 10 kg` is kept on a rough table as seen from above forces are appling on it as shown . Find the direction of static friction if the object does not move `(Take mu = 0.4)`
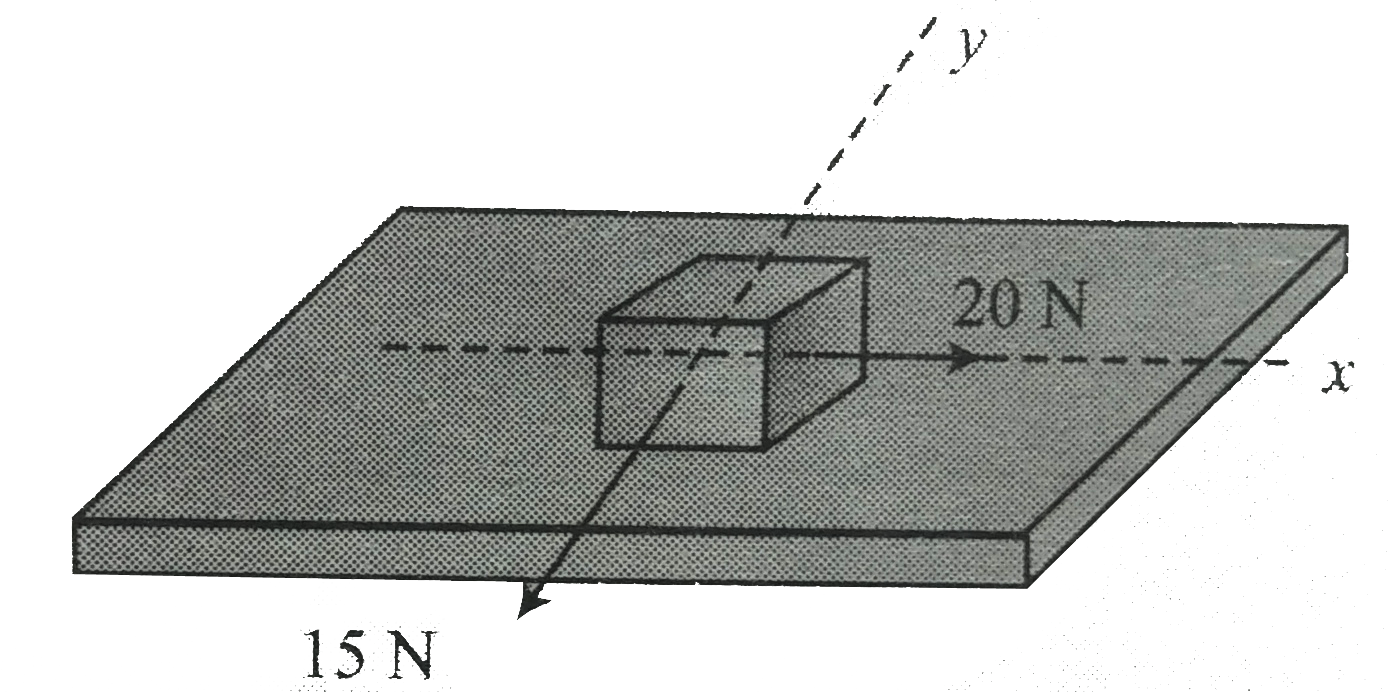 03:10View Solution
03:10View SolutionA block of mass 2 kg is pushed against a rough vertical wall with a force os 40 N. Coefficient of static friction being 0.5. Another horizontal force is 15 N, is applied on the block in a direction paralle to the wall. Will the block move? If yes in which direction? If no, find the frictional force exerted by the wall on the block.
07:15View SolutionDetermine the magnitude of frictional force and acceleration of the block in each of the following cases :
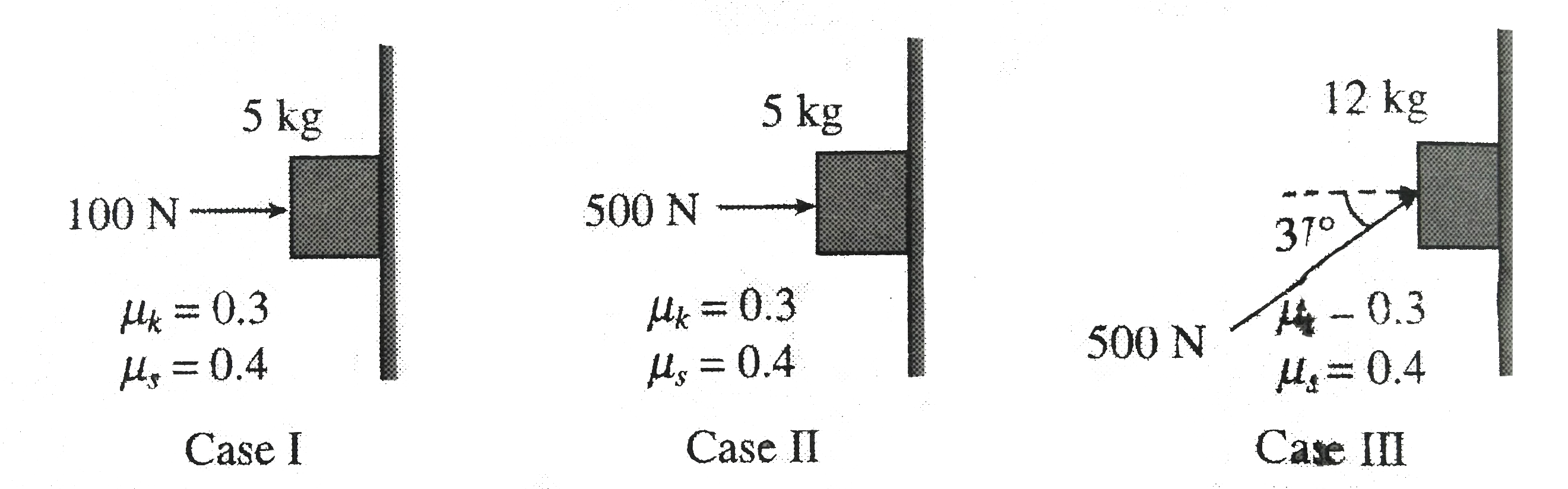 06:56View Solution
06:56View SolutionA block of mass `m` is supported on a rough wall by applying a force in figure Coefficient of static friction between block and wall is `mu`
For what range of value of `p` , the block remain in static equilibrium ?
 03:46View Solution
03:46View SolutionTwo blocks `A` and `B` are connected by a light inextensible string passing over a fixed smooth pulley as shown in figure The coefficient of friction between the block `A` and `B` the horizontal table is ` mu = 0.5 `. If the block `A` is just , find ratio of the masses of the blocks
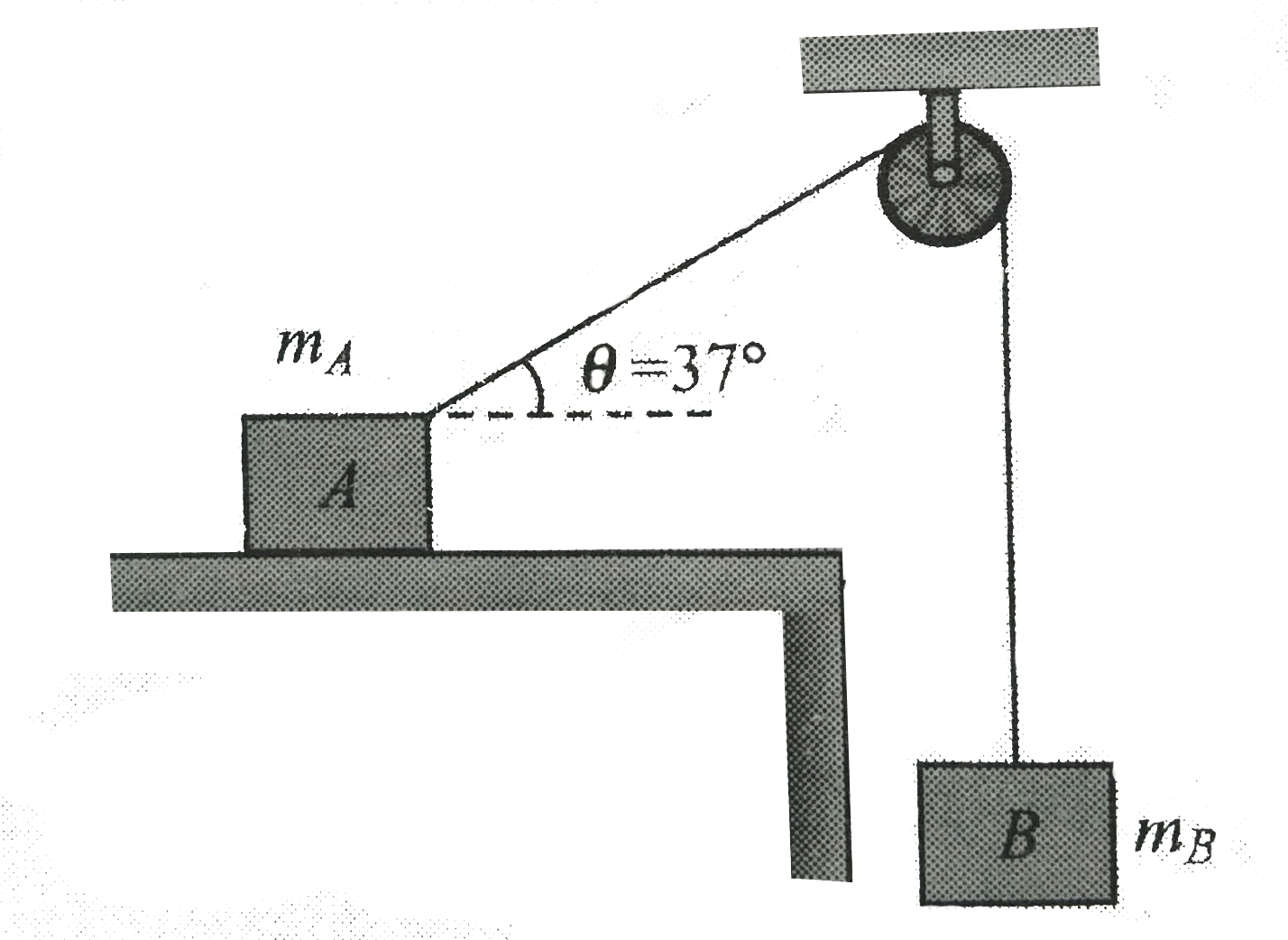 06:22View Solution
06:22View SolutionBlock A weighs `4 N` and block weigh `8 N` The coefficient of kinetic friction is `0.25` for all surface find the force `F` to slide `B` at a constant speed when (a)`A` rest on `B` and moves with it (b) `A` is held at rest and (c )`A and B` are connected by a light cord passing over a smooth putting as shown in fig 7.31 (a - c) restively.
 09:26View Solution
09:26View SolutionThe friction coefficient between the board and the floor shown in figure is `mu` Find the maximum force that the man can exert on the rope so that the board does not slip on the floor
 04:59View Solution
04:59View SolutionA block of mass `m` lying on a horizontal surface (coefficient of static friction `= mu_(s))` is to be brought into motion by a pulling force `F` At what angle `theta ` with the horizontal should the force `F` be applied so that its magnitude is minimum ? Also find the minimum magnitude
 05:33View Solution
05:33View SolutionA block of mass M is kept on as rough horizontal surface. The coefficient of static friction between the block and the surface is `mu`. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
07:57View SolutionA block lying on an inclined plane has a weigh of `50 N` .It just beings to side down when inclination of plane with the horizontal is `30^(@)` find the coefficient of static plane friction .
03:45View SolutionA block of mass `1 kg` is placed on a rough inclined plane at angle ` theta = 45^(@)` will horizontal . The block is connected with a straight as straight as shown in figure if `mu = 3//4` find the tension in string
 05:21View Solution
05:21View SolutionAn object of mass `10 kg` is to be kept at rest on an inclined plane making an angke of `37^(@)`to the horizontal by appling a force `F` along the plane upwards as shown in figure . The coefficent of static fiction between the object and the plane is `0.2` Find the magnitude of force `F`
[Take `g = 10 ms^(-2)]`
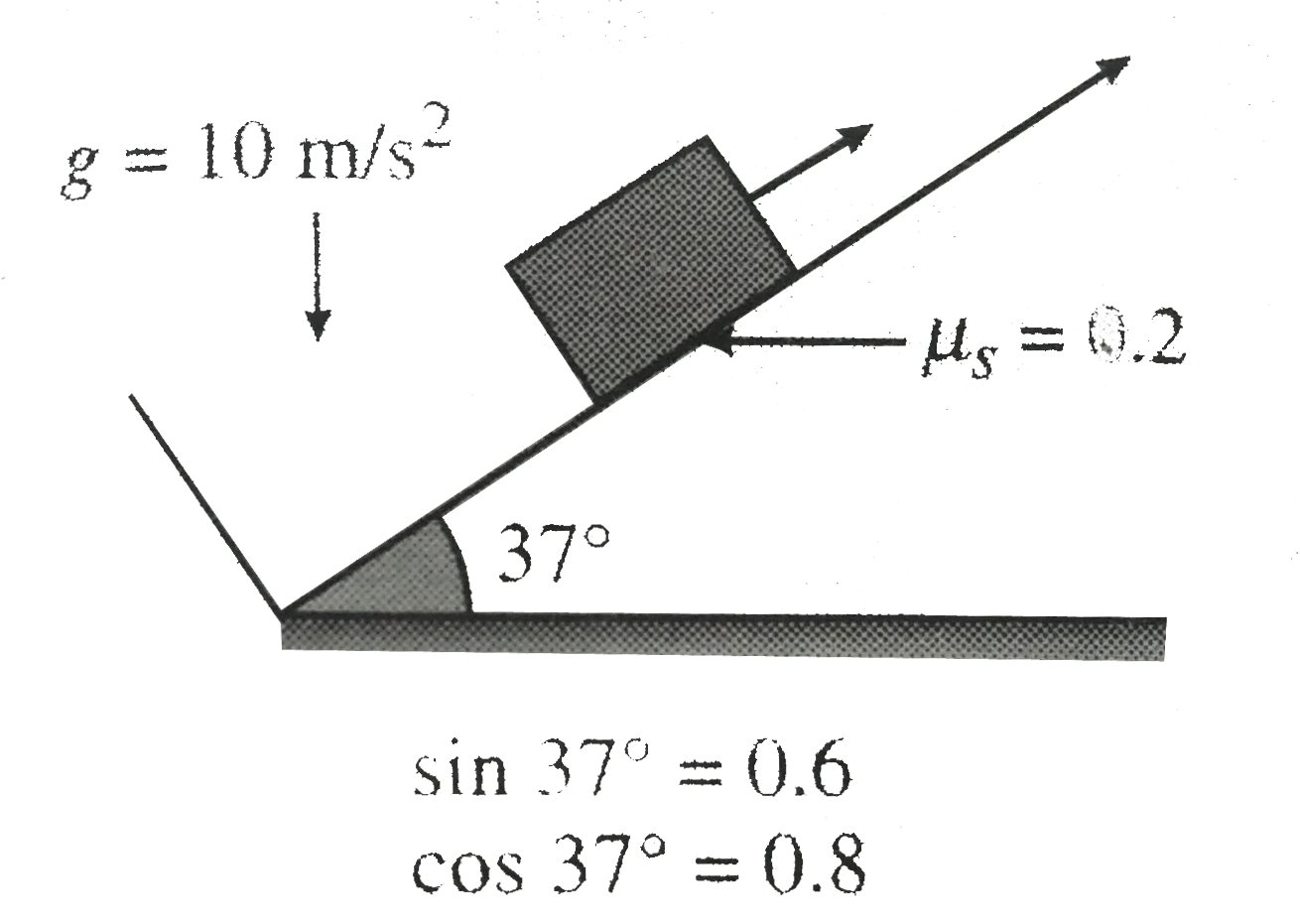 04:31View Solution
04:31View SolutionA `5 - kg` block sides down a plane inclined at `30^(@)` to the horizontal. Find
(a) The acceleration of the block if the plase is frictionless
b. The acceleration if the coefficient of kinetic friction is `1//2sqrt(3)`05:21View SolutionA `5 kg` block is projected upwards with an initial speed of `10 ms^(-1)` from the bottom of a plane inclined at `30^(@)` with horizontal . The coefficient of kinetic friction between the block and the plane is `0.2`
a. How far does the block move up the plane ?
b. How long does it move up the plate ?
c. After time from its projection does the block again come to the bottom ? What speed does it arrive?10:50View SolutionA block of mass `M = 10 kg ` is placed inclined plane , inclined at angle `theta = 37^(@)` with horizontal The coefficient of friction between the block and inclined is `mu = 0.5 `
a. Calculate the acceleration of the block when it is released
b. Now a force `F = 75 N` is appling on block as shown find out the acceleration of the block If the block is initially at rest .
c. In case (b), how much force should be added to `75 N` force so that block the starts to move up the incline.
d. In case (b), what is the minimum force by which `75N` force should be replaced with so that the block does not move?

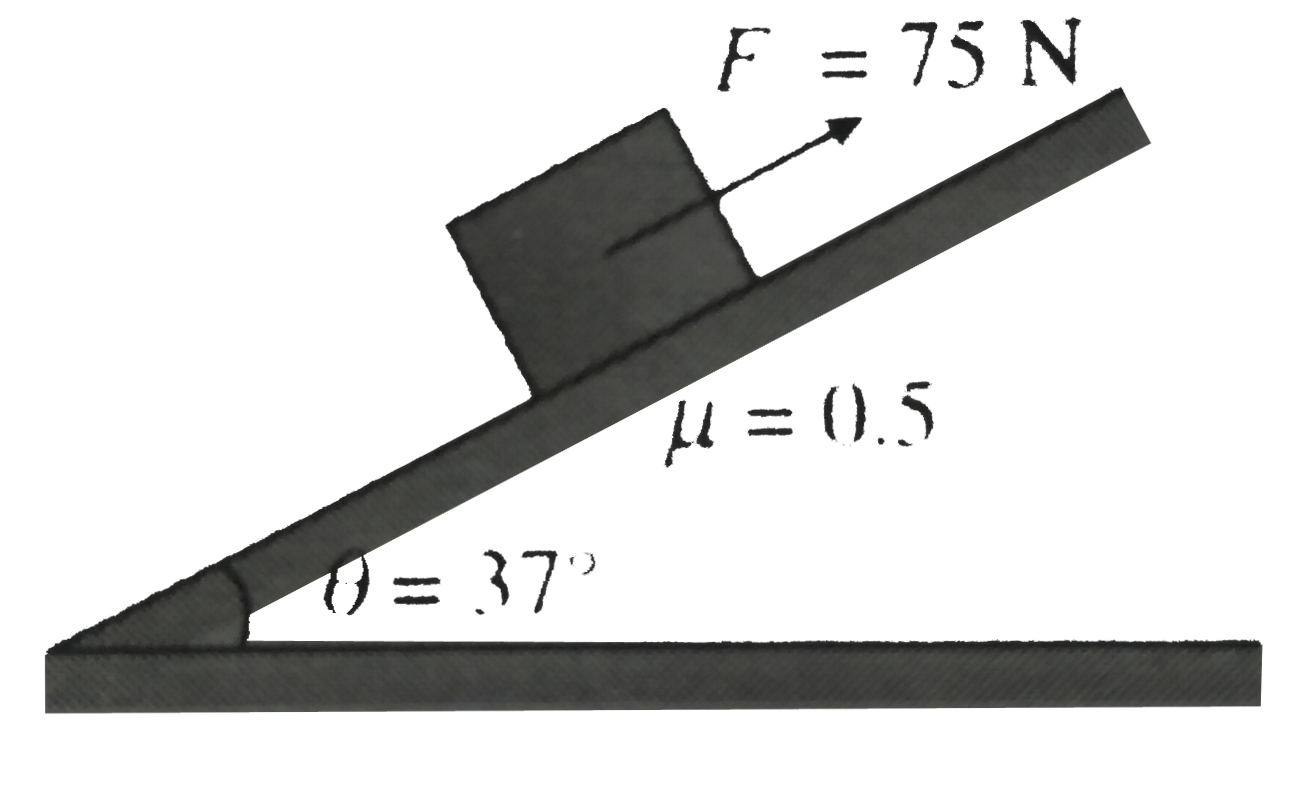 08:02View Solution
08:02View SolutionTwo block `M` and and m are arranged as shows in figure . If `M = 50 kg` then determine the minimum and maximum value of mass of block the heavy block `M` stationary
 07:09View Solution
07:09View SolutionTwo block `A and B` of mass `m_(A)= 10 kg` and `m_(A) = 20 kg ` are place on rough horizontal surface . The blocks are connected with a string. If the coefficient of fraction between block `A` and ground is ` mu _(A) = 0.9` and between block `B` and ground is `mu _(B) = 0.3 ` and the tension in the string in situation as shown in fig force `120 N `and `100 N` start acting when the system is at rest?
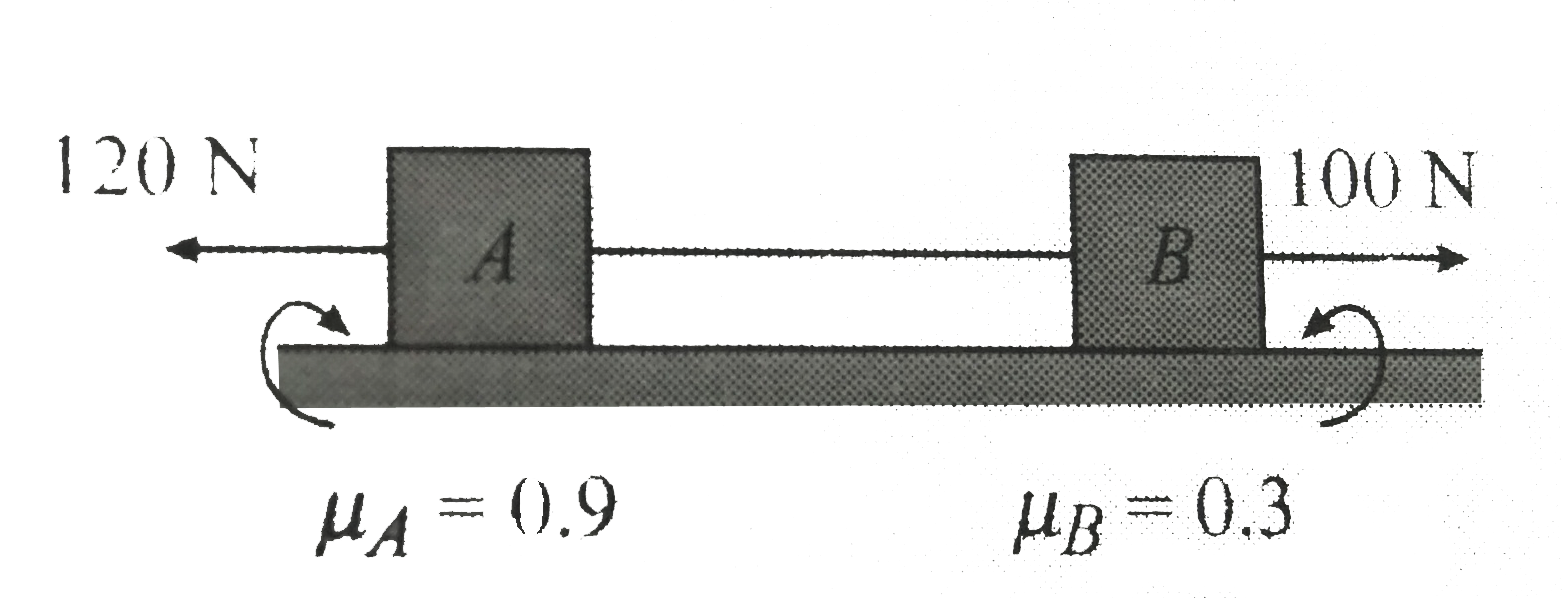 07:31View Solution
07:31View SolutionBlock `A` of mass `m` and block `B` of mass `2m` are placed on a fixed triangular wedge by means of a light and inextensible string and a frictionless pulley as shown in fig . The wedge is inclined at `45^(@)` to the horizontal on both sides . The coefficient of friction between the block `A`and the wedge is `2//3` and that between the block `B` and the wedge is `1//3` .If the system of `A and B` is released from rest then find .
a. the acceleration of `A`
b. tension in the string
c.the magnitude and direction of the frictional force acting on `A`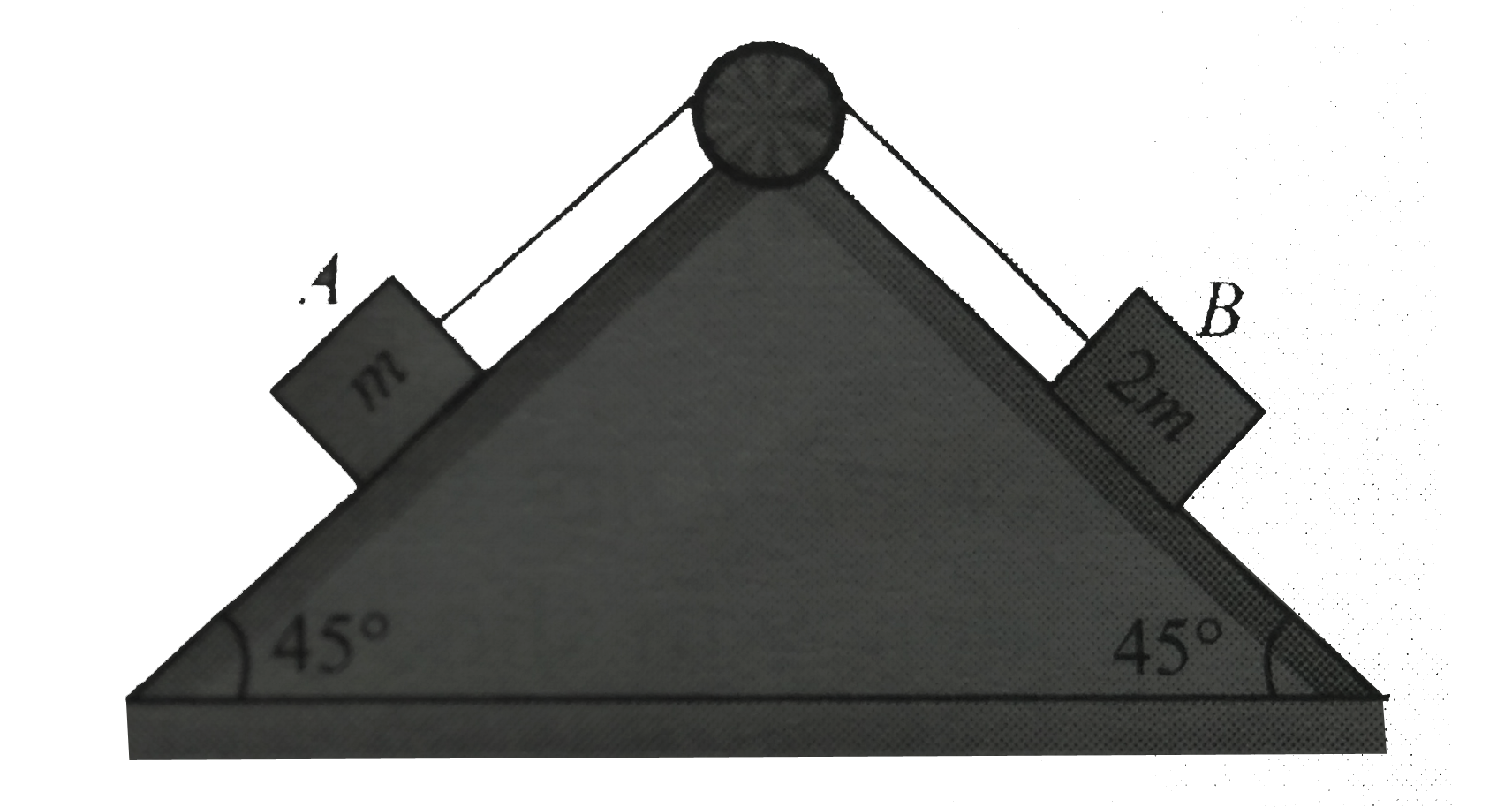 12:06View Solution
12:06View SolutionFigure shown two blocks in contact sliding down an inclined surface of inclination `30^(@)`. The block of mass `2 kg `and the incline is `mu_(1) = 0.20` and the incline is `mu_(2) = 0.30` .Find the acceleration of `2.0 kg` block (in `ms^(-2)`)`g = 10 ms^(-2)`
 04:24View Solution
04:24View SolutionTwo blocks `m_(1)` and `m_(2) ` are acted upon by the forces `F_(1)` and `F_(2) ` as shown in figure . If no relative sliding between is smooth , find the static friction between the blocks. Make necessary assumptions and discuss different cases.
 03:10View Solution
03:10View SolutionIn fig Block `m_(2)` is loaded on block `m_(1)` . If there is no relative sliding between the block and the inclined plane is smooth , find the friction force between the block
 02:23View Solution
02:23View SolutionThere are two block as shown in the figure of masses `1kg` and `4kg`. Friction coefficient between any two surfaces are `0.2` then find maximum value of horizontal force `F` so that both blocks moves together.
_2019_CBT6_E01_036_Q01.png) 07:02View Solution
07:02View SolutionLet as consider the next case in the previous illustration when there is no friction between ground and `M` . The coefficient of static and kinetic friction are `mu_(2)` and `mu_(1)`, respectively, and force `F` acts upper block as shown in figure
a. What is the maximum possible value of `F` so that the system moves together ?
b . If there is releative sliding between `M` and `m` then calculate acceleration of `M` and `m`
 05:07View Solution
05:07View SolutionTwo blocks `A` and `B` of mass `10 kg` and `20 kg` respectivelly, are arranged as shown in figure In the figure given a constant force `F_(0) = 120 N `act on block `A` and a force zero discoss the direction and nature of friction force and the acceleations of the block for different value of `F`
 04:59View Solution
04:59View SolutionIn the Fig force `F = alpha t ` is applied on the block of mass `m_(2)`. Here `alpha` is a constant and `t` is the time .Find the acceleration of the block Also draw the acceleration time graph of both the block
 08:33View Solution
08:33View SolutionThe masses of the blocks `A, B` and `C` shown in fig (a) are `4 kg, 2kg` and `2 kg` respectively Block `A` moves with an acceleration of `2.5 ms^(-2)`
a. Block `C` is removed from its in position and placed on block `A` (b). What is now the acceleration of block `C` ?
b. The position of the block `A` and `B` subsequently interchanged find the new acceleration of `C` .The coefficient of friction in the same for all the conect surface 05:56View Solution
05:56View SolutionIn the situation shown in fig
a. What minimum force `F` will make any part or whole system move?
b. Find the acceleration of two blocks and value of friction at the two surface if `F = 6 N` 04:44View Solution
04:44View Solution(a) Find the acceleration of the two block shown in figuer (b) Find the friction force between alll contant surface
 05:21View Solution
05:21View SolutionThe coefficient of friction between the block `A` of mass `m` and the triangular wedge `B` of mass `M` is `mu`. There in no friction between the wedge and the plane if the system (block `A+` wedge `B)` is released so that there is no stiding between `A` and `B` find the inclination `theta`
 02:39View Solution
02:39View SolutionA block `A` of mass` m` which is placed a rough inclined face of a wedge of same mass being pulled through light string and with force `F` as shown in figure The coefficient of friction between inclined face and block `A` is `mu ` while there is no friction between the ground and wedge it the whole system moves with same acceleration then find the value of `F`
 04:59View Solution
04:59View SolutionGiven the setup shown in Fig Block `A, B` and `C` have masses `m_(A)= M` and `m_(B) =m_(C) = m`. The strings are assumed maseless and unstreichable, and the pulleys frictionless .There is no friction between block `B` and the support table, but there is friction between blocks `B` and `C`, denoted by a given coefficient `mu`

a . In terms the given find (i) the acceleration of block `A` and `B`
b. Suppose the system is released from rest with block `C` near the right end of block `B` as shown in the above figure. If the the length `L` of block `B` is given, what is the speed of block `C` as it reached the left end of block `B` ? Tear the size of `C` as small
c. If the mass of block `A` is less then some critical value, the blocks will not accelerate when released from rest. Write down as expression for that critical mass.10:25View SolutionThe pulley of the system shown in Fig is massless and frictionless and thread and thread is inextensible Then horizontal surface over which block `C` is smooth while for all the remaining surface is `mu`

Calculate minimum acceleration a with which the system should be moved to the right so that suspented block `A`(mass m ) and `B` (mass `M` and `M gt m )`can remain stationary relative to `C `04:55View SolutionIn Fig the co - efficient of friction between the walls of block of mass `m` and the plank of mass `M` is `mu` The same co- efficient of friction is there between the plank and the horizontal floor The force `F` is of `100 N` and the masses `m` and `M` are of `1 kg` and `3kg` respectively Find the value of `mu `.If the block does not slip along the wall of the plank
 06:36View Solution
06:36View SolutionThe block of mass `M` and are arrenged as the situation in fig is shown.The coefficient of friction between two block is `mu`and that between the bigger block and the ground is `mu` find the acceleration of the block
05:19View SolutionA bar of mass `m` is placed on a triangular block of mass `M` as shown in figure The friction coefficient between the two surface is `mu` and ground is smooth find the minimum and maximum horizontal force `F` required to be applied on block so that the bar will not slip on the inclined surface of block
 09:10View Solution
09:10View SolutionA block of mass `1kg` is tied to a string of length `1m` the other end of which is fixed The block is moved on a smooth horizontal table with constant speed `10ms^(-1)`. Find the tension in the string
01:30View SolutionThe ball of mas `m` moves with speed `v` againest a smooth , fixed vertical circular groove of radius `R` kept on smooth horizontal surface find the
a. normal reaction of the floor or the ball.
b. normal reaction of the vertical wall on the ball.01:35View SolutionA block of mass `m` is kept on the edge of a horizontal turn table of radius `R` which is rotating with constant angular verticle `omega` (along with the block ) about its axis . If coefficient of friction is `mu`, find the friction force between block and table.
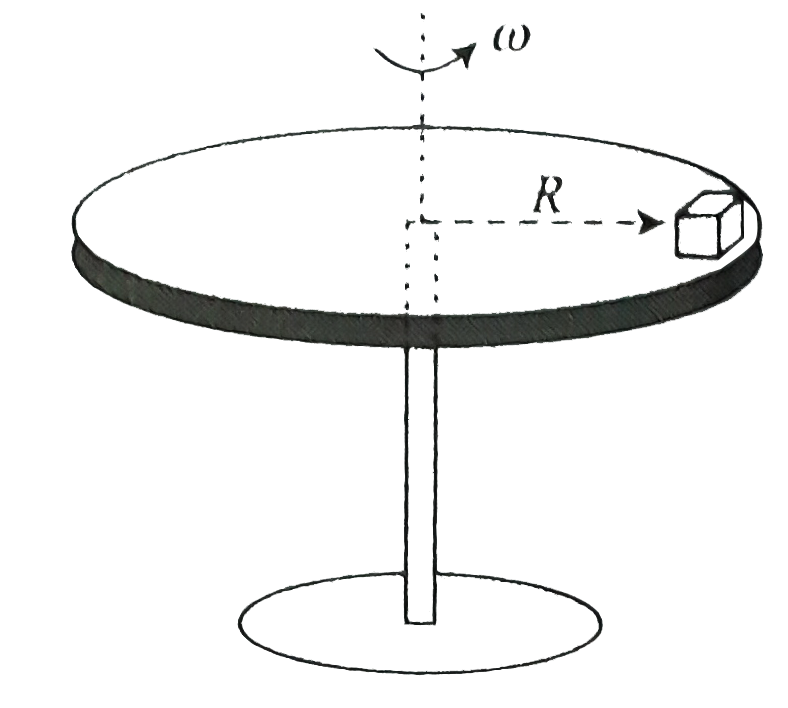 01:20View Solution
01:20View SolutionA car of mass `m` moving over a convex bridge of radius `r` .Find the normal reaction acting on car when it is at bighest point the bridge.
01:28View SolutionA car of mass `m` moving over a concave bridge of radius `r` .Find the normal reaction acting on car when it is at lowest point the bridge
01:12View SolutionA small block is connected to one of two identical massless strings of lengtth `16(2)/(3) cm` each with their ends fixed to a verticle rod If the ratio of tensions `T_(1)//T_(2)` is 4 : 1 ,then what will be the angular velocity of the block ? Take `g = 9.8ms^(-2)`
 06:37View Solution
06:37View SolutionTwo wires `AC and BC` are tied at `C` of small sphere of mass `5kg ` which revolves at a constant speed `v` in the horizontal circle of radius `1.6 m ` Find the maximum value of `v`
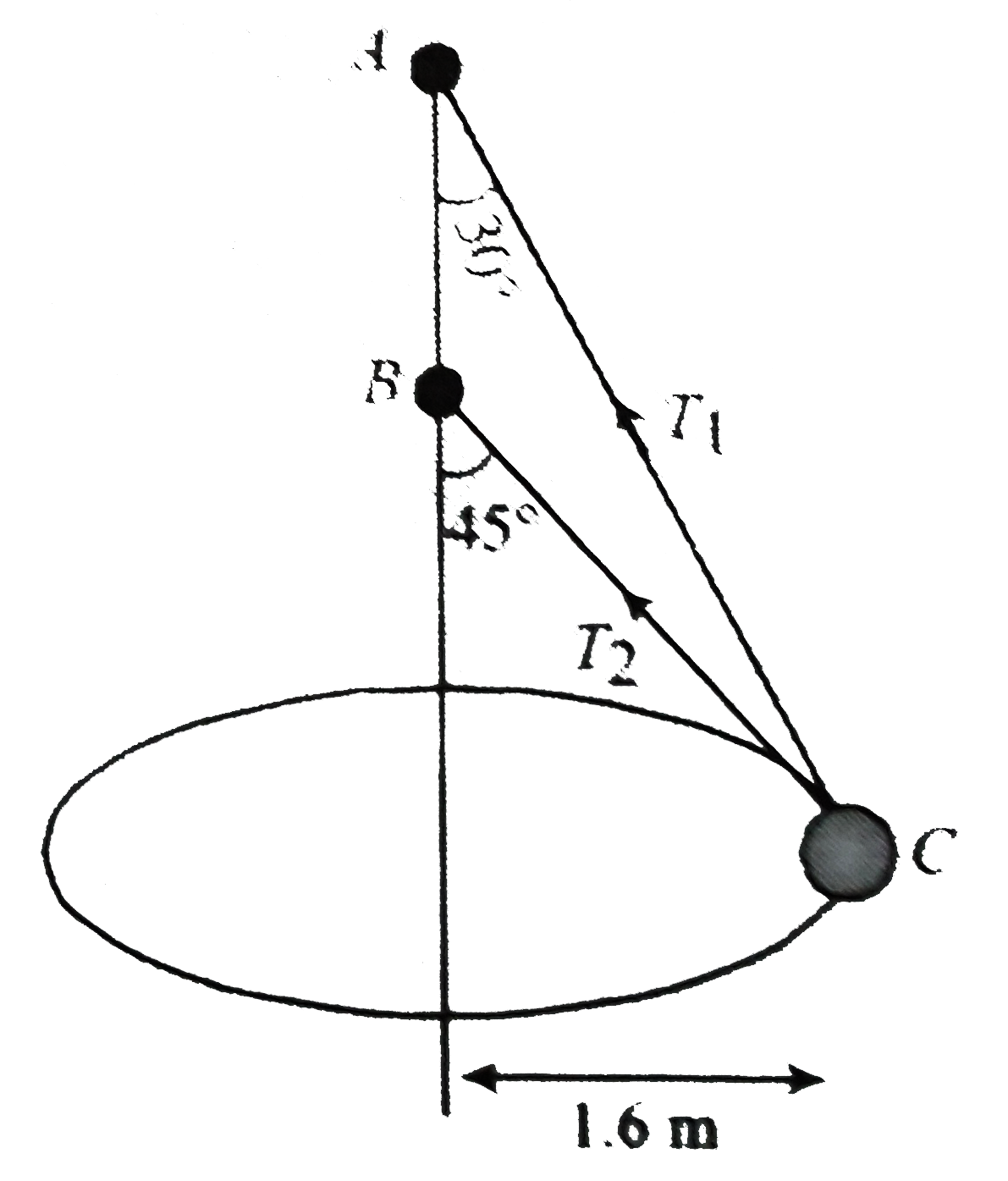 03:36View Solution
03:36View SolutionA turn has a radius of `10m` if a vehicle goes round it at an average speed of `18km//h` , what should be the proper angle of banking?
01:47View SolutionA turn of radius 20 m is banked for the vehicles going at a speed of 36km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?
07:45View SolutionA coin is pushed down tangentially from an angular position `theta ` on a cylindrical surface , with a velocity `v` as shown in figure If the coefficient of friction the coin and surface is `mu` find the tangential acceleration of the coin
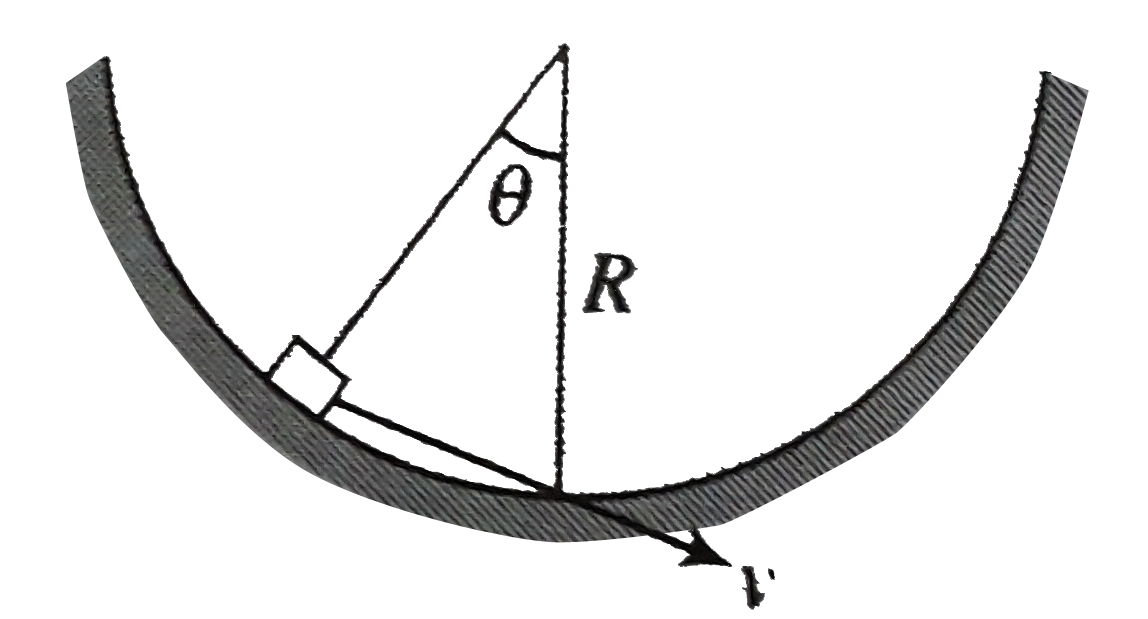 02:29View Solution
02:29View SolutionA particle of mass `m` is moving with a constant speed `v` in a circular path in a smooth horizontal plate (plan of the paper ) by a spring force as shown in figure If the natural length of the spring is `l_(0)` and stiffeness of the spring is `k` find the elongation of the spring
 04:28View Solution
04:28View SolutionA hemispherical bowl of radius R si set rotating abouv its axis of symmetry whichis kept vertical. A small blcok kept in the bowl rotates with the bowl without slippingn on its surface. If the surfaces of the bowl is mooth, and the abgel made by the radius through the block with the vertical is `theta`, find the angular speed at which the bowl is rotating.
04:17View SolutionA block of mass `m` is kept on rough horizontal turn table at a distance r from the center of table. The coefficient of friction between torn table and block is `mu` Now the turn - table starts rotating with uniform angular acceleration a
a. Find the time after which slipping accure between block and turn - table
b. Find the angle made by friction force at the point of slipping05:20View SolutionA particle of mass `m` connected with a hanging bob of mass `M` by an inextensible string is stationary relative to the rotating platform . The coefficient of static friction between the particle and platform is `mu`

Find the
a. maximum angular speed `omega_(1)`
b. maximum angular speed `omega_(2)`
`(for M gt mu m)`06:35View SolutionIn fig two block of mass `m_(A) and m_(B)` are rotating at radius `r` kept on a rough table consider friction `(mu)` between all the contact surface pulley is frictionless determine the angular speed of the turn table for which the blocks just begin to slide
 06:20View Solution
06:20View SolutionAn inclined plane of angule a is fixed onto a horizontal turntable with its line of greater slope in same plane as a diameter of forntable .A small block is placed on the inclined plane a distance `r` from the axis the coefficient of fraction between the block and the inclined plane is `mu` The turntable along with incline plane spins about its axis with constant minimum angular velocity `omega`
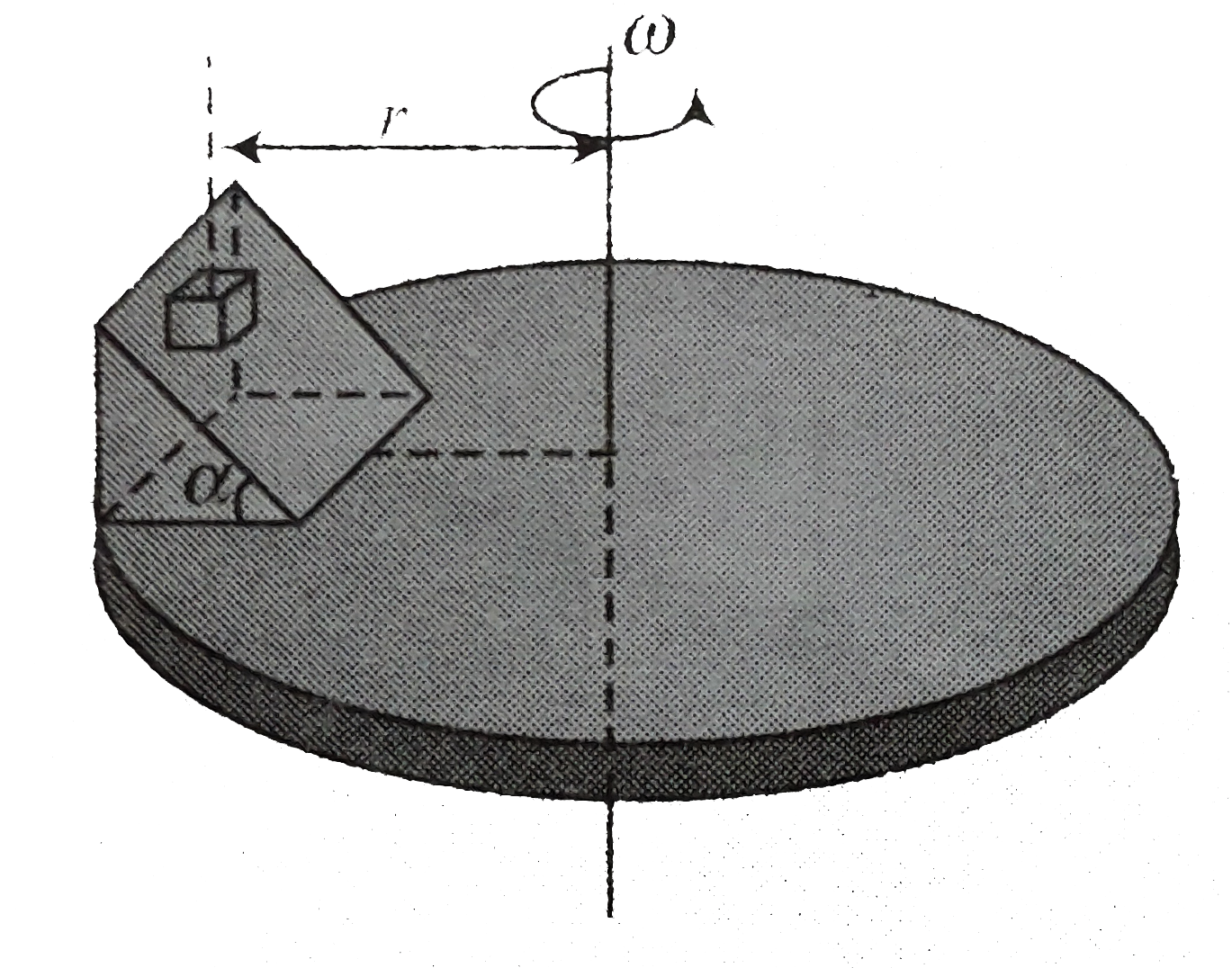
a. Find an capression for the minimum angular velocity `omega` to prevent the block from sliding down the plane in term of `g, r, mu ` and the plane `omega`
b. Now a block of mass but having coefficient friction (with inclined plane)`2mu` is kept instead of the original block . find the radius of friction force acting between block and incline now to the friction force active in part (a)05:11View SolutionA motorcycle has to move with a constant speed on an overbridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.
a. what can its maximum velocity be for which the contact with the road is not broken at the highest point?
b. If the motorcycle goes at speed `1/sqrt2` times the maximum found in part a. where will it lose the contact with the road?
c. What maximum uniform speed can it maintain on the bridge if it does not lose contact anywhere on the bridge?09:44View SolutionA coin is pushed down tangentially from position `theta` on a cylindrical surface with a velocity `v` as shown in Fig. If the coefficient of friction between the coin and surface is `mu` find the tangential acceleration of the coin
 05:58View Solution
05:58View SolutionIn the situation shown in fig
a. What minimum force `F` will make any part or whole system move?
b. Find the acceleration of two blocks and value of friction at the two surface if `F = 6 N` 04:44View Solution
04:44View SolutionA block of mass `1kg` is tied to a string of length `1m` the other end of which is fixed The block is moved on a smooth horizontal table with constant speed `10ms^(-1)`. Find the tension in the string
01:30View Solution
Illustration questions and complete solutions for chapter NEWTON'S LAWS OF MOTION 2 of CENGAGE PHYSICS (HINGLISH) of Class 11
