Complete Solutions to Excercises of chapter VECTORS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | VECTORS |
| CP SINGH | Excercises |
| Number Of Questions | 66 |
| Academic Year | 2023-24 |
A vector is not changed if
03:11View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
02:28View SolutionTwo vectors acting through a point are in the ratio `3 : 5`. If the angle between them is `60^(@)` and the magnitude of their resultant is `35` , find the magnitude of vectors.
03:09View SolutionThe magnitude of vectros `vec A`,` vec B` and `vec C` are 12, 5 and 13 units respectively and ` vec A + vec B= vec C`, find the angle between ` vec A and vec B` .
02:21View SolutionIf `vec(A)=vec(B)+vec(C )`, and the magnitudes of `vec(A)`,`vec(B)`,`vec(C )` are 5,4, and 3 units, then the angle between `vec(A)` and `vec(C )` is
03:30View SolutionTwo forces, while acting on particle in opposite directions,have the resultant of 10N. If they act at right angles to each other, the resultant is found to be 50N. Find the two forces?
04:53View SolutionOne of the following forces is double and the other resultant is equal to the greater force. The angle between them is
02:09View SolutionTwo vectors of magnitude `4` and `6` are acting through a point. If the magnitude of the resultant is `R`
02:29View SolutionThe resultant of `vecA and vecB` makes an angle `alpha` with `vecA` and `beta and vecB`,
01:50View SolutionWhich of the sets given below may represent the magnitudes of three vectors adding to zero?
08:22View SolutionThe following sets of three vectors act on a body, whose resultant can be zero. These are :
00:44View SolutionThree vectors `vec(P) , vec(Q)` and `vec( R)` are such that `|vec(P)| , |vec(Q )|, |vec(R )| = sqrt(2) |vec(P)|` and `vec(P) + vec(Q) + vec(R ) = 0`. The angle between `vec(P)` and `vec(Q) , vec(Q)` and `vec(R )` and `vec(P)` and `vec(R )`are
05:12View SolutionThree forces ` 9 , 12` and `15 N` acting at a point are in equilibrium . The angle between `9 N` and `15 N` is
03:20View SolutionIf the resultant of `n` forces of different magnitudes acting at a point is zero, then the minimum value of `n` is
02:09View SolutionLet `vec(C )= vec(A)+vec(B)` then
02:43View SolutionForces of `1` and `2 units` act along the lines `x = 0` and ` y = 0`. The equation of the line of action of the resultant is
02:06View SolutionThe sum of two forces at a point is 16N. if their resultant is normal to the smaller force and has a magnitude of 8N, then two forces are
03:02View SolutionA particle is being acted upon by four forces of `30 N` due east , `20 N` due north , `50 N` due west and `40 N` due south. The resultant force will be
05:49View SolutionSix vector `vec(a)` through `vec(f)` have the magnitudes and direction indicated in the figure. Which of the following statements is true?
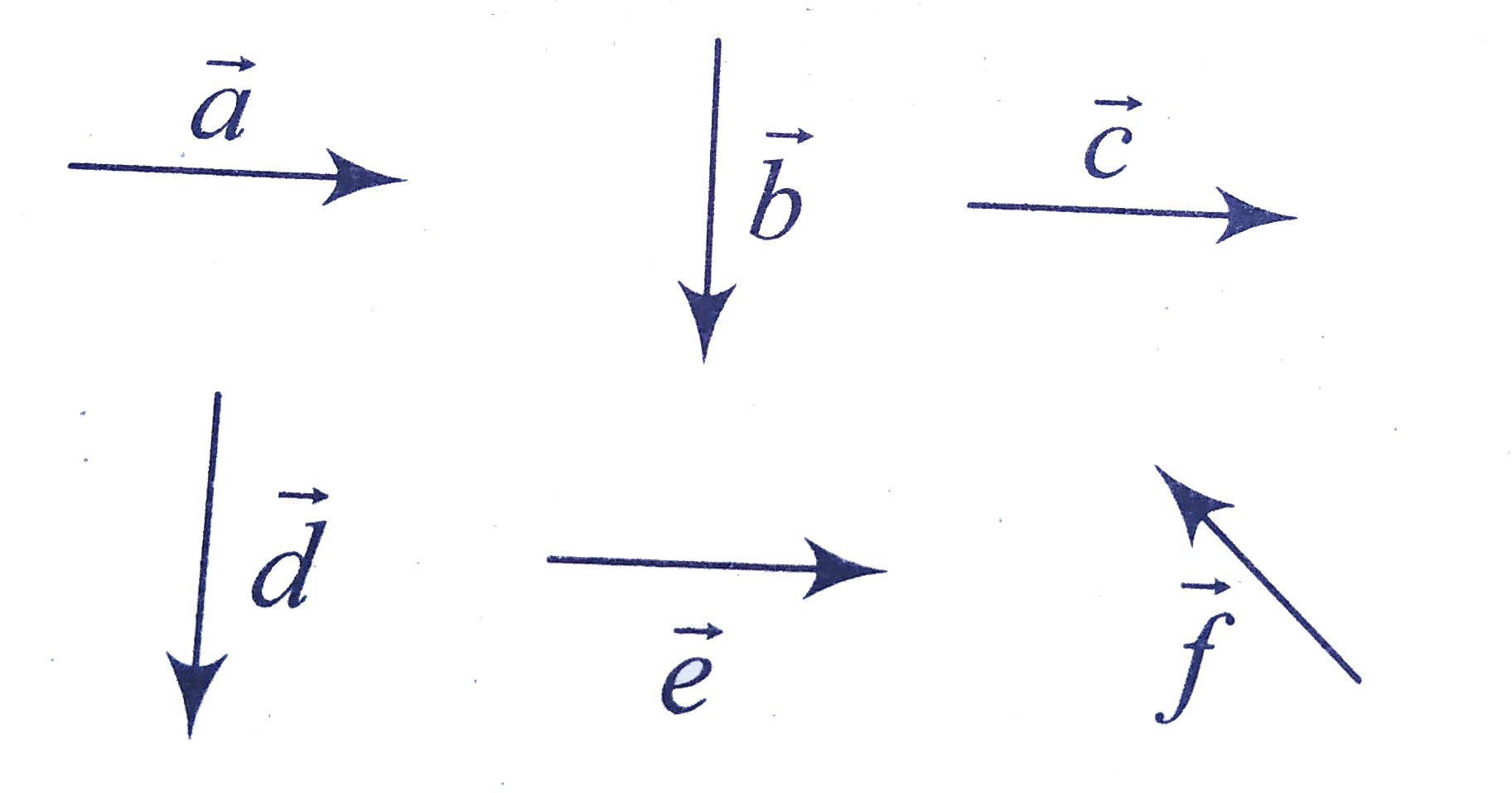 01:58View Solution
01:58View SolutionIf N-vectors of equal magnitude are acting through a point and angle between the adjacent vectors is `2pi//N` , find the resultant.
05:35View SolutionFive equal forces of `10 N` each are applied at one point and all are lying one plane. If the angles between them are equal, the resultant force will be
04:11View SolutionForces proportional to `AB , BC` and `2 CA` act along the slides of a triangle `ABC` in magnitude and direction by
02:09View Solution`ABCDEF` is a regular hexagon, Fig. 2 (c ) .65. What is the value of
` (vec (AB) + vec (AC) + vec (AD) + vec (AE) + vec (AF) ?`
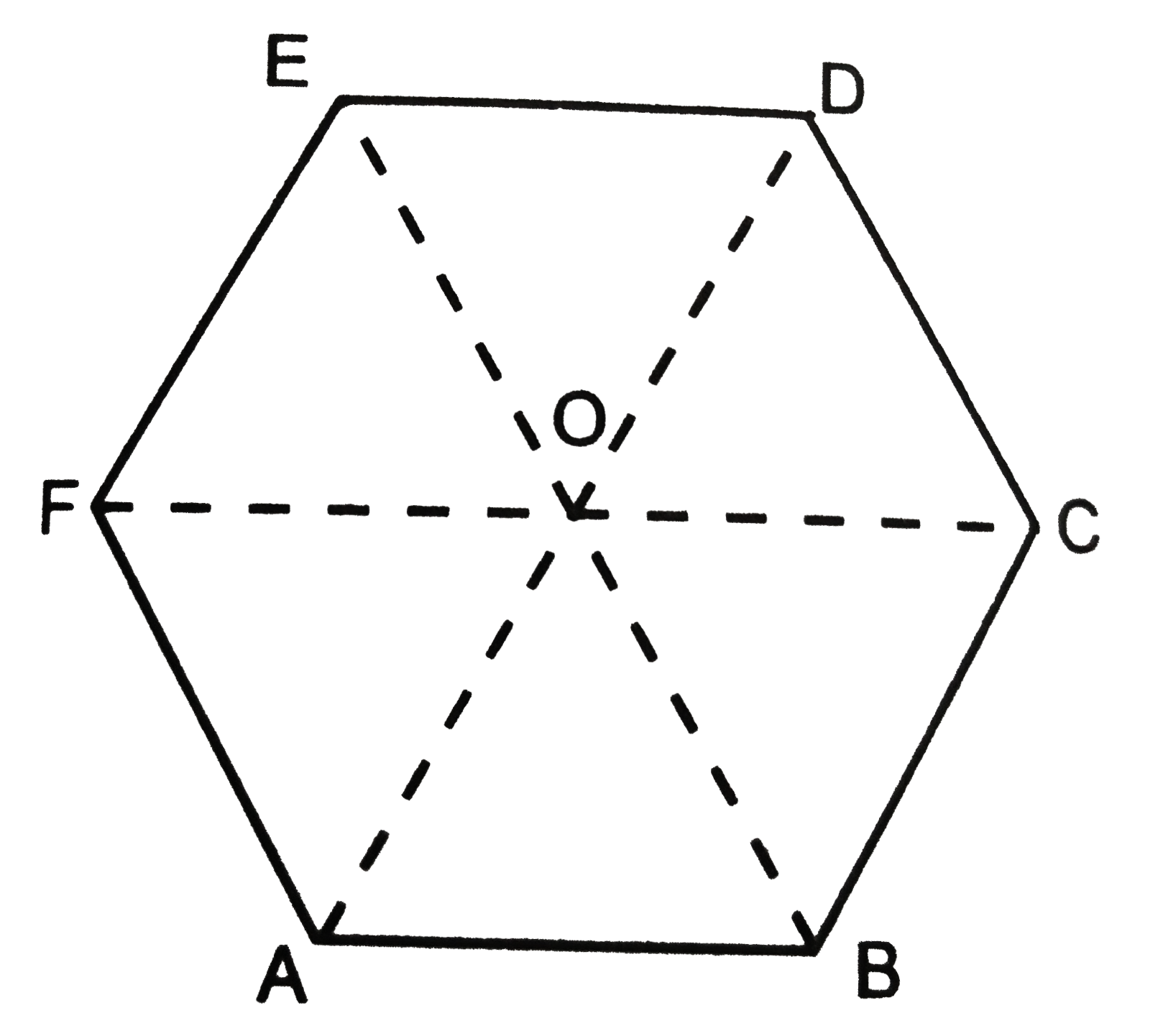 .06:14View Solution
.06:14View SolutionA truck travelling due to north at `20m s^(-1)` turns west and travels at the same speed. Find the change in its velocity.
02:22View SolutionA particle moves towards east with velocity `5m//s`. After `10 seconds` its direction changes towards north with same Velocity. The average acceleration of the particle is
03:54View SolutionThe length of second's hand in watch is `1 cm`. The change in Velocity of its tip in 15 seconds is
05:09View SolutionAparticle moves with a speed `v` changes direction by an angle `theta`, without change in speed.
01:59View SolutionLet the angle between two non - zero vectors `vec(A)` and `vec(B)` be `120^(@)`and its resultant be `vec( C)`.
02:42View SolutionThe component of a vector is
02:07View SolutionOne of the two rectangular components of a force is `20 N` and it makes an angle of `30^(@)` with the force. The magnitude of the other component is
01:38View SolutionWhile travelling from one station to another , a car travels `75 "km north"` , `60 "km north - east"` and `20 "km east"`. The minimum distance between the two station is
04:43View SolutionA person moves `30 m` north, then `30 m est, then 30sqrt(2)` south-west. His diaplacement from the original position is
01:43View SolutionFind the resultant of the three vectors `vec(OA), vec(OB)` and `vec(OC)` shown in figure. Radius of the circle is R.
 03:57View Solution
03:57View SolutionThree forces acting on a body are shown in figure. To have the resultant force only along the y-directon, the magnitude of the minimum additional force needed si
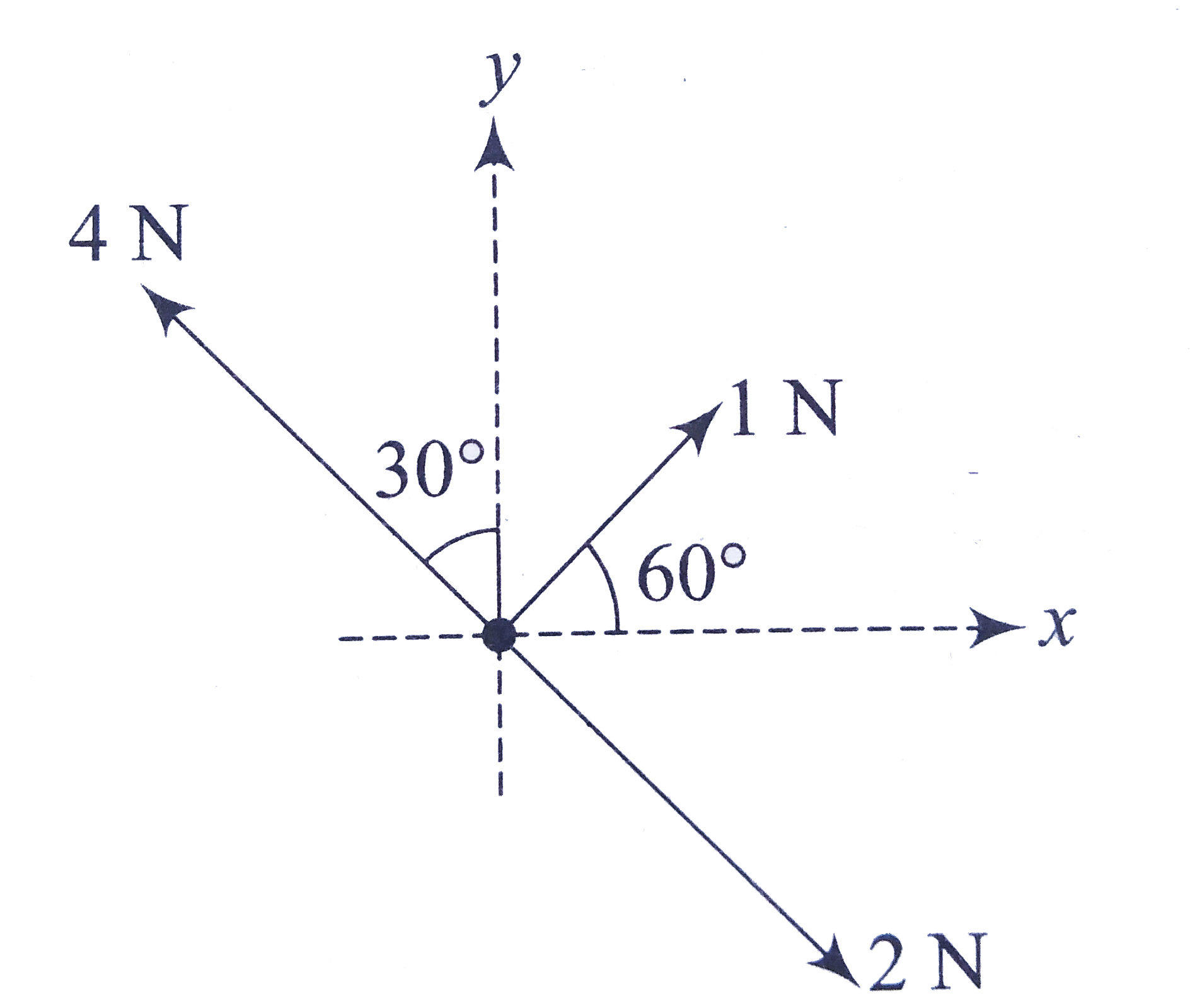 02:43View Solution
02:43View SolutionThe `x`- component of the resultant of several vectors
(i) is equal to the sum of the `x`-components of the vectors
(ii) may be smaller than the sum of the magnitudes of the vectors
(iii) may be greater than the sum of the magnitudes of the vectors
(iv) may be equal to the sum of the magnitudes of the vectors02:14View SolutionA hall has the dimensions `10 m xx 12 m xx 14 m`. A fly starting at one corner ends up at a diagonally opposite corner. What is the magnitude of its displacement
02:16View SolutionIf a unit vector is represented by `0.5 hat(i) + 0.8 hat(j) + c hat(k)` , then the value of `c` is
01:25View SolutionIf `vec(A) = 3 hat(i) - 4 hat(j)` and `vec(B) = 2 hat(i) + 16 hat(j)` then the magnitude and direction of `vec(A) + vec(B)` will be
02:06View SolutionIf a particle moves from the point `A(1 , 2 , 3)` to the point `B( 4 , 6 ,9)`, its displacement vector be
02:15View SolutionThe unit vector parallel to the resultant of the vectors `vec(A) = hat(i) + 2 hat(j) - hat(k)` and `vec(B) = 2 hat(i) + 4 hat(j) - hat(k)` is
02:05View SolutionIf `vec(A) = 3 hat(i) + 6 hat(j) - 2hat(k)` , the directions of cosines of the vector `vec(A)` are
02:26View SolutionIf a vector `vec(A)` make angles `alpha , beta ` and `gamma`, respectively , with the `X , Y` and `Z` axes , then `sin^(2) alpha + sin^(2) beta + sin^(2) gamma =`
02:05View SolutionIf the sum of two unit vectors is a unit vector,then find the magnitude of their differences.
03:22View SolutionWhat is the angle between `vec(A)` and the esultant of `(vec(A) + vec(B))` and `(vec(A) - vec(B))`
01:48View SolutionA paricle starting from the origin (0,0) moves in a straight line in `(x,y)` plane. Its coordinates at a later time are `(sqrt(3),3)`. The path of the particle makes with the x-axis an angle of
01:23View SolutionIf for two vectors `vec(A)` and `vec(B)`, sum `(vec(A)+vec(B))` is perpendicular to the difference `(vec(A)-vec(B))`. Find the ratio of their magnitude.
02:26View SolutionIf a vector `2 hat (i) + 3 hat(j) + 8 hat(k)` is perpendicular to the vector `- 4 hat(i) + 4 hat(j) + alpha(k)`. Then the value of `alpha` is
02:21View SolutionWhich of the following vectors is//are perpendicular to the vector `4 I - 3 j` ?
03:19View SolutionIf `vec(A) = 2 I + j - k , vec(B) = I + 2 j + 3 k` , and `vec(C ) = 6 i - 2 j - 6 k`,then the angle between `(vec(A) + vec(B))` and `vec(C )` will be
03:07View SolutionVectors which is perpendicular to `( a cos theta hat (i) + b sin theta hat(j))` is
03:53View SolutionTwo vectors `vec A and vecB` have equal magnitudes.If magnitude of `(vecA+vecB)` is equal to n times of the magnitude of `(vecA-vecB)` then the angle between `vecA and vecB` is :-
06:49View SolutionThe position vector of a particle is `vec( r) = a cos omega t i + a sin omega t j`, the velocity of the particle is
02:57View SolutionThe component of vector `A= 2hat(i)+3hat(j)` along the vector `hat(i)+hat(j)` is
02:03View SolutionThe vector component of vector `vec(A) = 3 hat(i) + 4 hat(j) + 5 hat(k)` along vector `vec(B) = hat(i) + hat(j) + hat(k)` is
03:12View SolutionIf `vec(A)xxvec(B)=vec(C )`, then which of the following statements is wrong?
01:51View SolutionThe magnitude of the vectors product of two vectors `|vecA| and |vecB|` may be
01:24View SolutionThree vector `vec(A)`,`vec(B)`, `vec(C )` satisfy the relation `vec(A)*vec(B)=0`and `vec(A).vec(C )=0`. The vector `vec(A)` is parallel to
02:56View SolutionA vector `vec(A)` is along the positive `x`- axis . If `B` is another vector such that `vec(A) xx vec(B)` is zero , then `B` could be
02:23View SolutionA vector `vec(A)` points verically upward and `vec(B)` points towards north. The vector product `vec(A) xx vec(B)` is
02:14View SolutionThe value of `(vec(A)+vec(B))xx(vec(A)-vec(B))` is
03:29View SolutionThe scalar product of two vectors is `2 sqrt(3)` and the magnitude of their vector product is `2`. The angle between them is
01:47View SolutionIf `|vec(A)xxvec(B)|=sqrt(3)vec(A).vec(B)`, then the value of `|vec(A)+vec(B)|` is
02:04View SolutionThe angle between the vector `vec(A)` and `vec(B)` is `theta`. Find the value of triple product `vec(A).(vec(B)xxvec(A))`.
02:26View SolutionWhat is the unit vector perpendicular to the following vectors` 2 hat(i) + 2 hat(j) - hat(k)` and `6 hat(i) - 3 hat(j) + 2 hat(k)`
02:57View SolutionTwo adjacent sides of a parallelogram are respectively by the two vectors `hat(i)+2hat(j)+3hat(k)` and `3hat(i)-2hat(j)+hat(k)`. What is the area of parallelogram?
02:43View SolutionThe minimum number of vectors having different planes which can be added to give zero resultant is
01:36View Solution
Excercises questions and complete solutions for chapter VECTORS of CP SINGH PHYSICS (HINGLISH) of Class 11
