Complete Solutions to EXERCISES of chapter NEWTONS LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION |
| CP SINGH | EXERCISES |
| Number Of Questions | 84 |
| Academic Year | 2023-24 |
Action and reaction
(i) act on two different objects
(ii) have equal magnitude
(iii) have opposite directions
(iv) have resultant zero01:02View SolutionA body of 5kg is moving with a velocity of 20m/s. If a force of 100N is applied on it for 10 s in the same direction as its velocity, what will now be the velocity of the body?
00:58View SolutionA car moving with a velocity of 10m/s can be stopped by the application of a constant force F In a distance of 20m. If the velocity of the car is 30m/s. It can be stopped by this force in
01:40View SolutionA ball of mass 0.2 kg is thrown vertically upwards by applying a force by hand. If the hand moves 0.2 m while applying the force and the ball goes upto 2 m height further, find the magnitude of the force. (Consider `g=10m//s^2`).
03:42View SolutionA force vector applied on a mass is represented as `vec(F)=6hat(i)-8hat(j)+10hat(k)` and acceleration with `m//s^(2)`. What will be the mass of the body in kg.
01:06View SolutionA body of mass `2kg` moving on a horizontal surface with an initial velocity of `4 ms^(-1)` comes to rest after `2` second. If one wants to keep this body moving on the same surface with a velocity of `4 ms^(-1)` the force required is
04:07View SolutionA body of mass 1 kg is moving towards east with a uniform speed of 2m/s. A force of 2N is applied to it towards north. The magnitude of the displacement of the body 2s after the force is applied is
04:10View SolutionA force `F_1` acts on a particle so as to accelerate it from rest to a velocity v. The force `F_1` is then replaced by `F_2` which decelerates it to rest
02:41View Solutionwhich of the following is correct order fo forces?
01:12View SolutionA solid sphere of mass 2 kg is resting inside a cube as shown in fig. The cube is moving with a velocity `vec(v)=(5t hat(i)+2t hat(j))ms^(-1)`. Here t is time in seconds. All surface are smooth. The sphere is at rest with respect to the cube. What is the total force exerted by the sphere on the cube?
 03:23View Solution
03:23View SolutionA particle of mass m is at rest at the origin at time `t=0` It is subjected to a force `F(t)=F_(0)e^(-bt)` in the X-direction. Its speed `V(t)` is depicted by which of the following curves
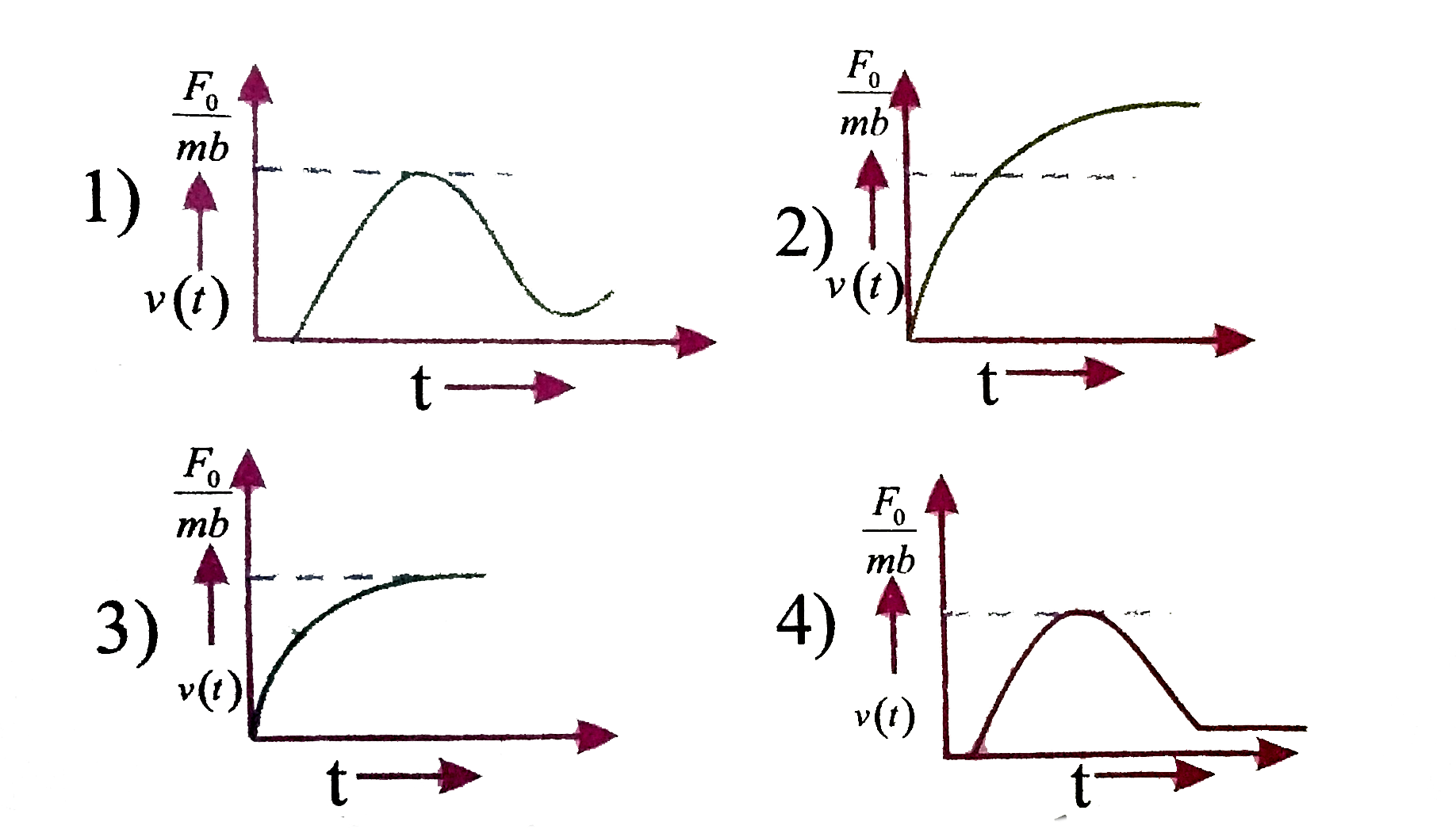 03:17View Solution
03:17View SolutionTwo bodies of mass 3kg and 4kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (`g=9.8m//s^(2)`)
01:16View SolutionTwo masses `m_(1)` and `m_(2)` are connected by a light string passing over a smooth pulley. When set free `m_(1)` moves downward by 2 m in 2 s. The ratio `m_(1)//m_(2)` is
02:30View SolutionIn fig the blocks A,B,and C of mass m each have acceleration `a_(1),a_(2), and a_(3)`, repectively. `F_(1) and F_(2)` are external force of magnitude `2mg and mg`, respectively. Then
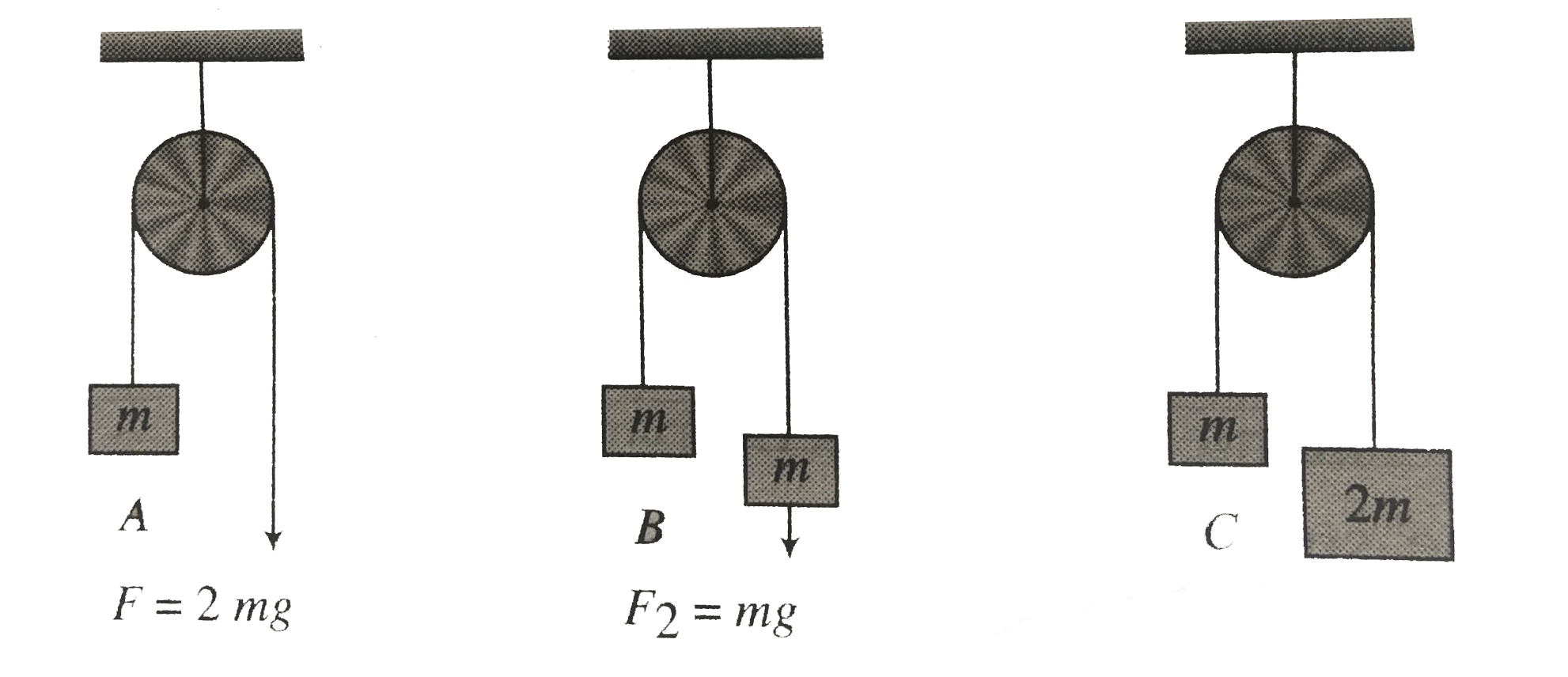 04:09View Solution
04:09View SolutionThree equal weight `A,B` and `C` of mass `2kg` each are hanging on a string passing over a fixed frictionless pulley as shown in the figure. The tension in the string connecting weights `B` and `C` is approximately
 02:11View Solution
02:11View SolutionTwo blocks are connected by a string as shown in the diagram. The upper block is hung by another string. A force F applied on the upper string produces an acceleration of `2m//s^(2)` in the upward direction in both the blocks . If T and T' be the tensions in the two parts of the string, then
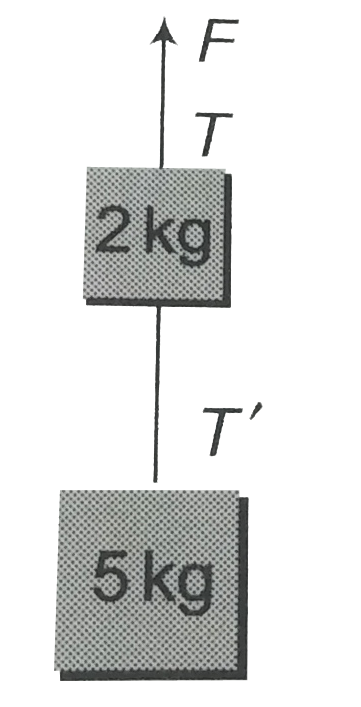 01:50View Solution
01:50View SolutionFour identical blocks each of mass m are linked by threads as shown. If the system moves with constant acceleration under the influence of force F, the tension `T_(2)` is
 01:23View Solution
01:23View SolutionA block of mass `m_(1)` rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass `m_(2)`. The acceleration of the system is
01:19View SolutionA uniform chain of mass 2 kg hangs from a light pulley with unequal lenghts of the chain hanging from the two sides of the pulley. The force exerted by the moving chain on the pulley is
05:36View SolutionA string of negligible mass going over a clamped pulley of mass m supports a block of mass M as shown in the figure. The force on the pulley by the clamp is given by
 03:33View Solution
03:33View SolutionA body sliding on a smooth inclined plane requires `4s` to reach the bottom, starting from rest at the at the top. How much time does it take to cover ont-foruth the distance startion from rest at the top?
02:53View SolutionA particle starts sliding down a frictionless inclined plane. If ` S_(n) ` is the distance travelled by it from time ` t = n-1 sec `, to `t = n sec`, the ratio ` (S_(n))/(s_(n+1))` is
05:25View SolutionA block of mass 10kg is pushed up on a smooth incline plane of inclination `30^(@)`, so that it has acceleration `2m//s^(2)`. The applied force is
01:48View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
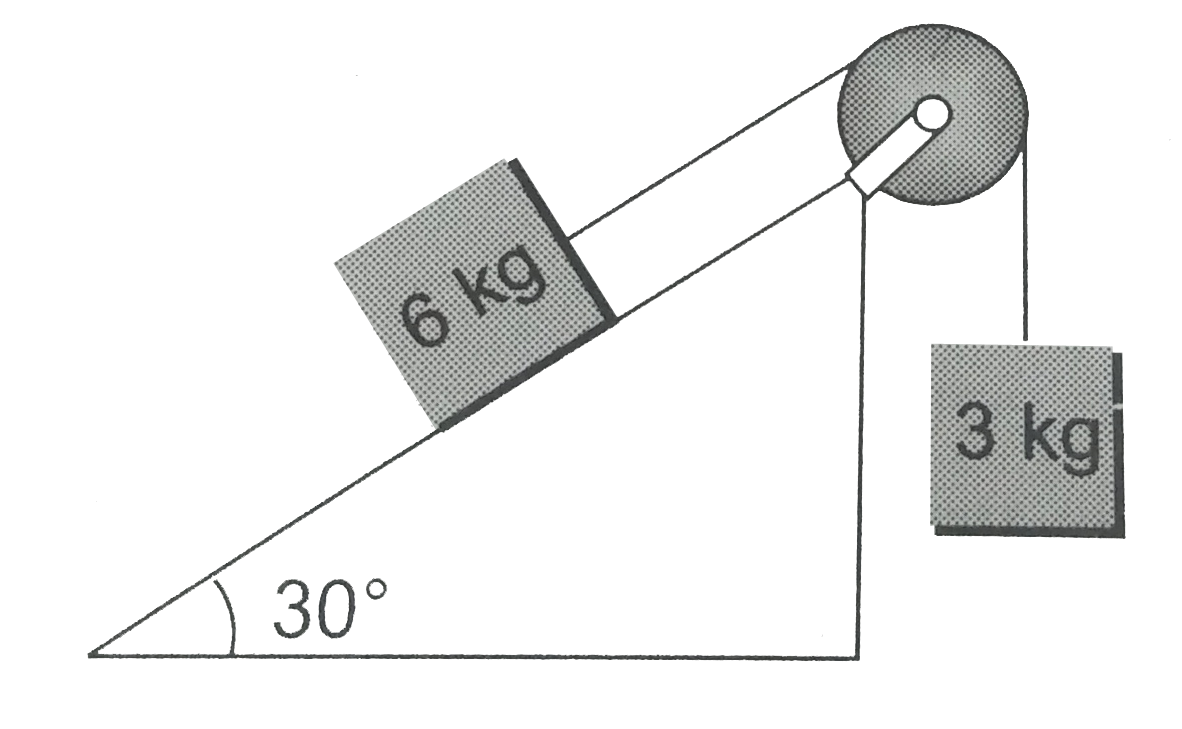 01:34View Solution
01:34View SolutionThe acceleration of system over the wedge as shown in the figure is
 01:49View Solution
01:49View SolutionA rope of length 5 m is kept on frictionless surface and a force of 5 N is applied to one of its end. Find the tension in the rope at 1 m from this end
02:52View SolutionA uniform rope of length of length `L` is pulled by a force `F` on a smooth surface. Find tension in the rope at a distance `x` from the end where force is applied.
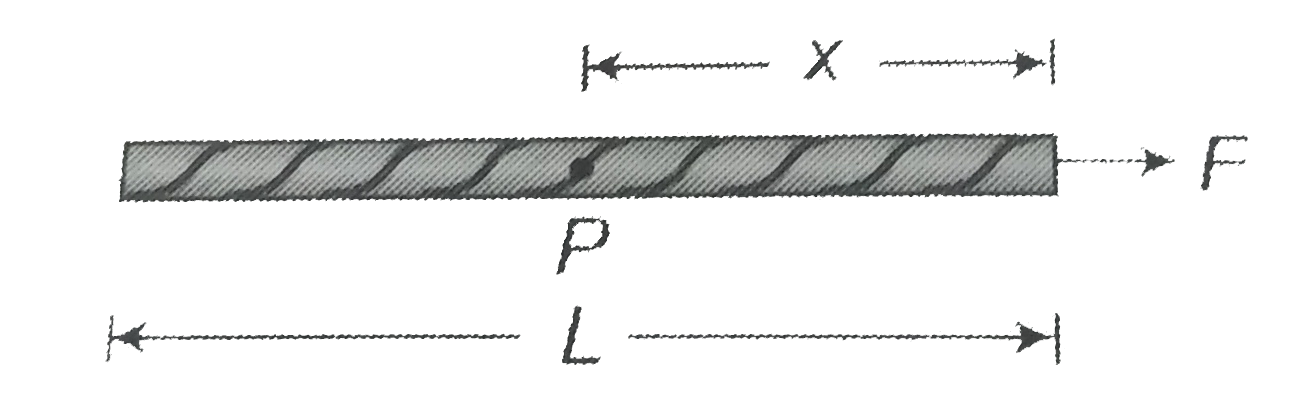 02:15View Solution
02:15View SolutionA block of mass `M` is pulled along a horizontal frictionless surface by a rope of mass `m` . Force P is applied at one end of rope. The force which the rope exerts on the block is:
06:51View SolutionIn the previous problem if M=2m, the tension in the middle of the rope is
02:22View SolutionConsider the situation as shown in the figure. The system is free to move.

The force by the rope on the block is `FM//(M+m)`04:40View SolutionA monkey of mass `20kg` is holding a vertical rope. The rope will not break when a mass of `25kg` is suspended from it but will break it the mass exeeds `25kg` . What is the maximum acceleration with which the monkey can climb up along the rope? `(g=10m//s^(2))` .
03:29View SolutionA man slides down a light rope whose breaking strength is `eta` times his weight (`etalt1`) . What should be his minimum acceleration so that the rope just breaks?
01:43View SolutionBlocks A and B have masses of 2 kg and 3 kg. respectively. The ground is smooth. P is an external force of 10 N. The force exerted by B on A is
 01:44View Solution
01:44View SolutionThree block of masses `m_(1),m_(2)` and `m_(3)` kg are placed in contact with each other on a frictionless table. A force F is applied on the heaviest mass `m_(1)`, the acceleration of `m_(2)` will be
 01:05View Solution
01:05View SolutionAll the surface are smooth and the strings ans pulleys are light. The force exerted by the 20 cm part of the rod on the 10 cm part is
 02:27View Solution
02:27View SolutionA block is kept on a frictionless inclined surface with angle of inclination `alpha`. The incline is given an acceleration 'a' to keep the block stationary. Then a is equal to
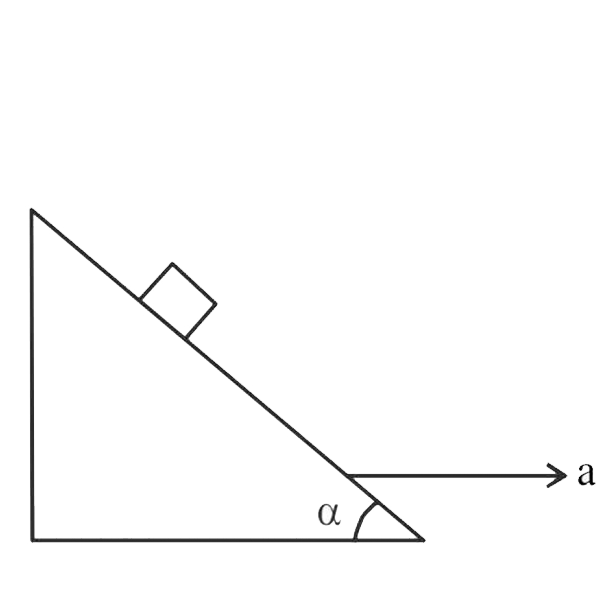 04:39View Solution
04:39View SolutionA body kept on a smooth inclined plane having inclination 1 in x will remain stationary relative to the inclined plane if the plane is given a horizontal accelertion equal to
02:06View SolutionA block of mass m is placed on a smooth wedge of incination `theta`. The whole system s acelerated horizontally so tht the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude
06:36View SolutionA man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?
 01:47View Solution
01:47View SolutionA painter is raising himself and the crate on which he stands with an acceleration of `5m//s^(2)` by a massless rope and pulley arrangement. Mass of the painter is 100 kg and that of the crate is 50 kg. If `g=10m//s^(2)`, then the

(i) tension in the rope is 2250 N
(ii) tension in the rope is 1125 N
(iii) force of contact between the painter and the flow 750 N
(iv) force of contact between the painter the paniter and the floor 375 N.02:43View SolutionIn the given diagram, with what force must the man pull the rope to hold the plank in position? Weight of the man is 60 kg. Neglect the weight of plank, rope and pulley.
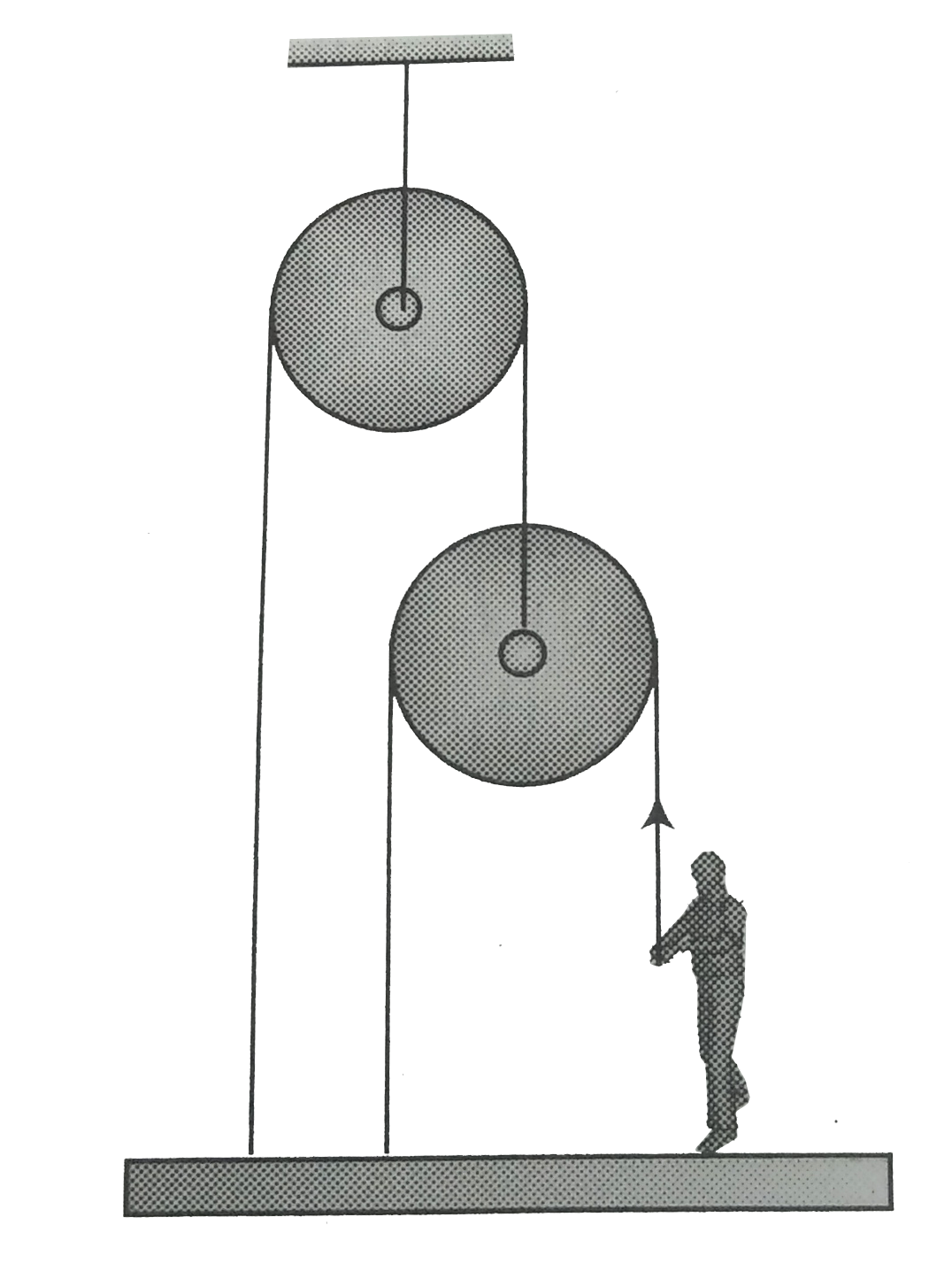 01:28View Solution
01:28View SolutionThe mass of a lift is `2000kg` . When the tensioon in the supporting cable is `28000N` , then its acceleration is.
01:54View SolutionIn an elevator moving vertically up with an acceleration g, the force exerted on the floor by a passanger of mass M is
01:09View SolutionA man weighs `80kg` . He stands on a weighing scale in a lift which is moving upwords with a uniform acceleration of `5m//s^(2)` . What would be the reading on the scale?
03:13View SolutionA person is standing in an elevator. In which situation he finds his weight less ?
02:04View SolutionThe force exerted by the floor of an elevator on the foot of a person standing there is more than the weight of the person if the elevator is
04:04View SolutionA lift is moving down with acceleration a. A man in the lift drops a ball inside the lift. The acceleration of the ball as observed by the man in the lift and a man standing stationary on the ground are respectively
02:16View SolutionA person standing oin the floor of an elevator drops as coin. The coin reaches the floor of the elevator in a time `t_1` if the elevator is stationary and in the `t_2` if it is moving uniformly. Then
03:14View SolutionAn elevator car whose floor to ceiling distance is equal to `2.7 m` starts ascending with constant acceleration `1.2 m//s^(2)`, 2 sec after the start a bolt begins falling from the ceiling of the car. Answer the following question `(g=9.8 m//s^(2))`
The bolt's free fall time is16:48View SolutionA lift is moving in upward direction. The totol mass of the lift an the passengers is 1600 kg. The variation of the velocity of the lift is as shown in the figure. The tension in the rope at `t=8^(th)` second will be
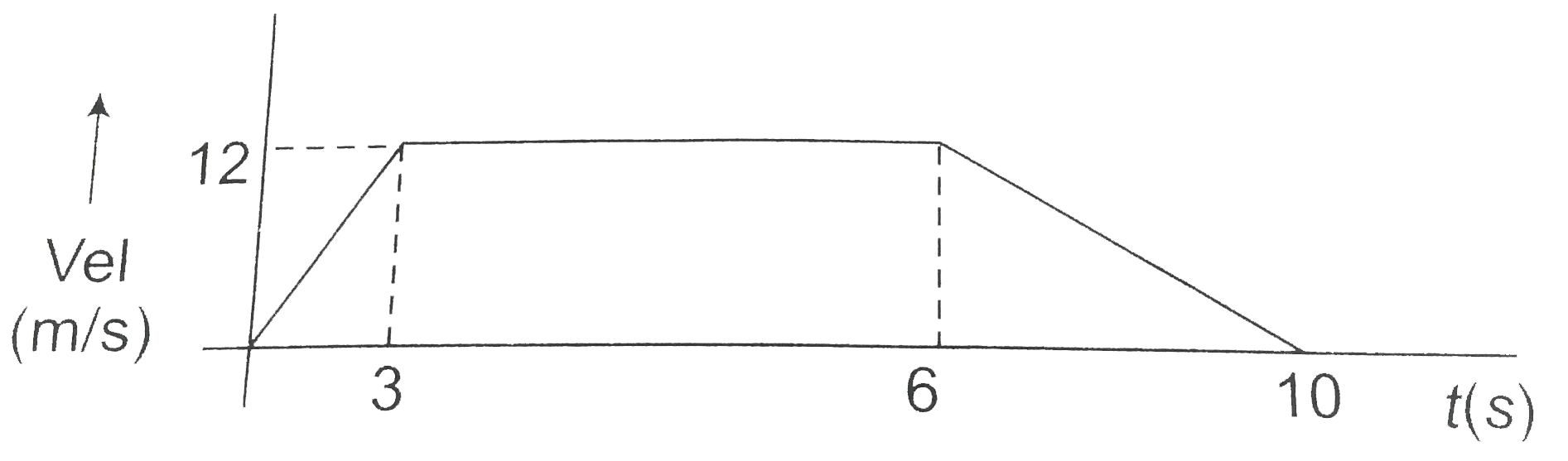 01:44View Solution
01:44View SolutionIn the previous problem, the height to which the lift takes the passenger is
01:39View SolutionAn empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
07:10View SolutionA balloon carring some sand is moving down with a constant acceleration `a_(0)`. How much mass of sand should be removed, so that the balloon move up with same acceleration?
02:39View SolutionTwo particles each of mass `m` are connected by a light string of length `2L` as shown in the figure. A constant force `F` is applied continuoulsly at the mid`-`point of the string at right`-`angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is `2x`
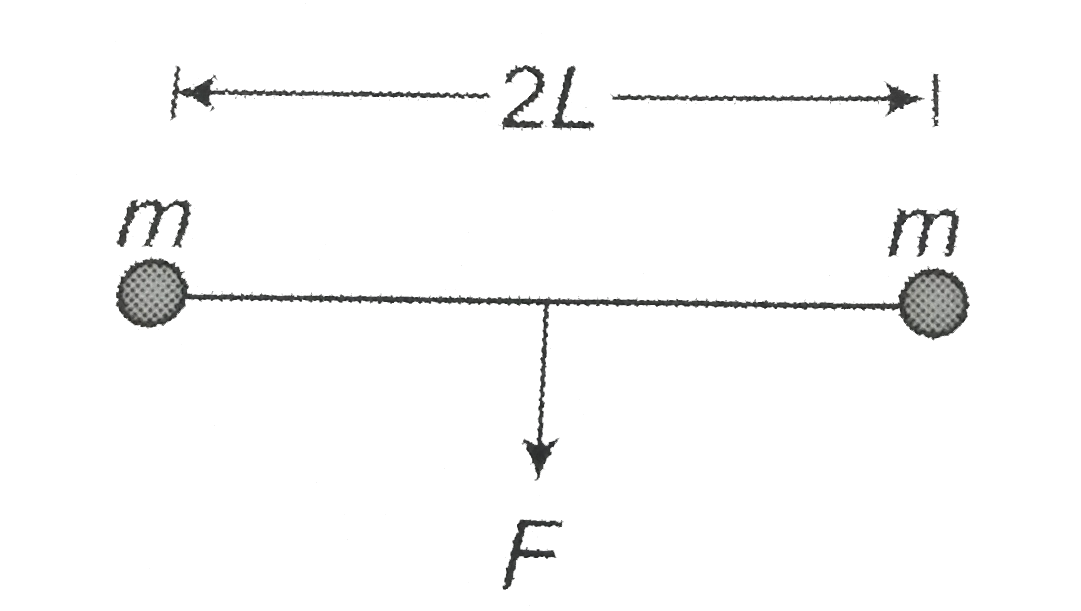 02:40View Solution
02:40View SolutionA force `vecF=vecvxxvecA` is exerted on a particle in addition to the force of gravity, where `vecv` is the veocity of the particle and `vecA` is a constant vector in the horizontal direction. With what minimum speed a particle of mass m be projected so that it continues to move undeflected with a constant velocity?
03:12View SolutionA mass of 1kg is suspended by a string A. Another string C is connected to its lower end (see figure). If a sunsudden jerk is given to C, then
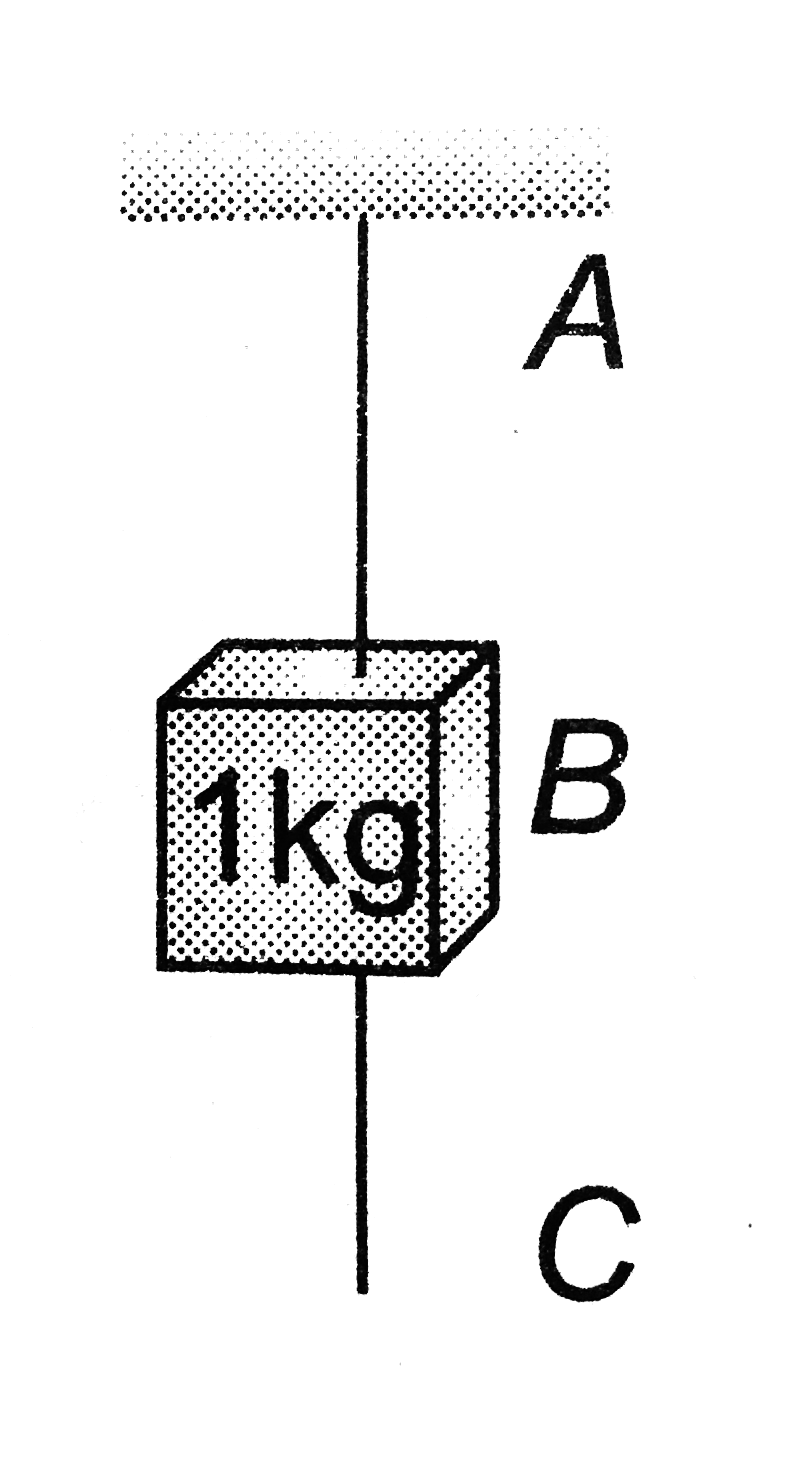 01:59View Solution
01:59View SolutionIn the previous problem, If the string C is stretched slowly, then
02:34View SolutionA stone is dropped from the top of a building in a high wind. The wind exerts a steady horizontal force on the stone as it falls. The path of the string is
01:43View SolutionA smooth wedge A is fitted in a chamber hanging from a fixed ceiling near the earth's surface.A block B placed at the top of the wedge takes a time T to slide down the length of the wedge. If the block is placed at the top of the wedge and the cable supporting the chamber is broken at the same instant, the block will
03:36View SolutionA body is in equilibrium under the action of three coplanar forces `P,Q and R` as shown in figure. Select the correct statement.
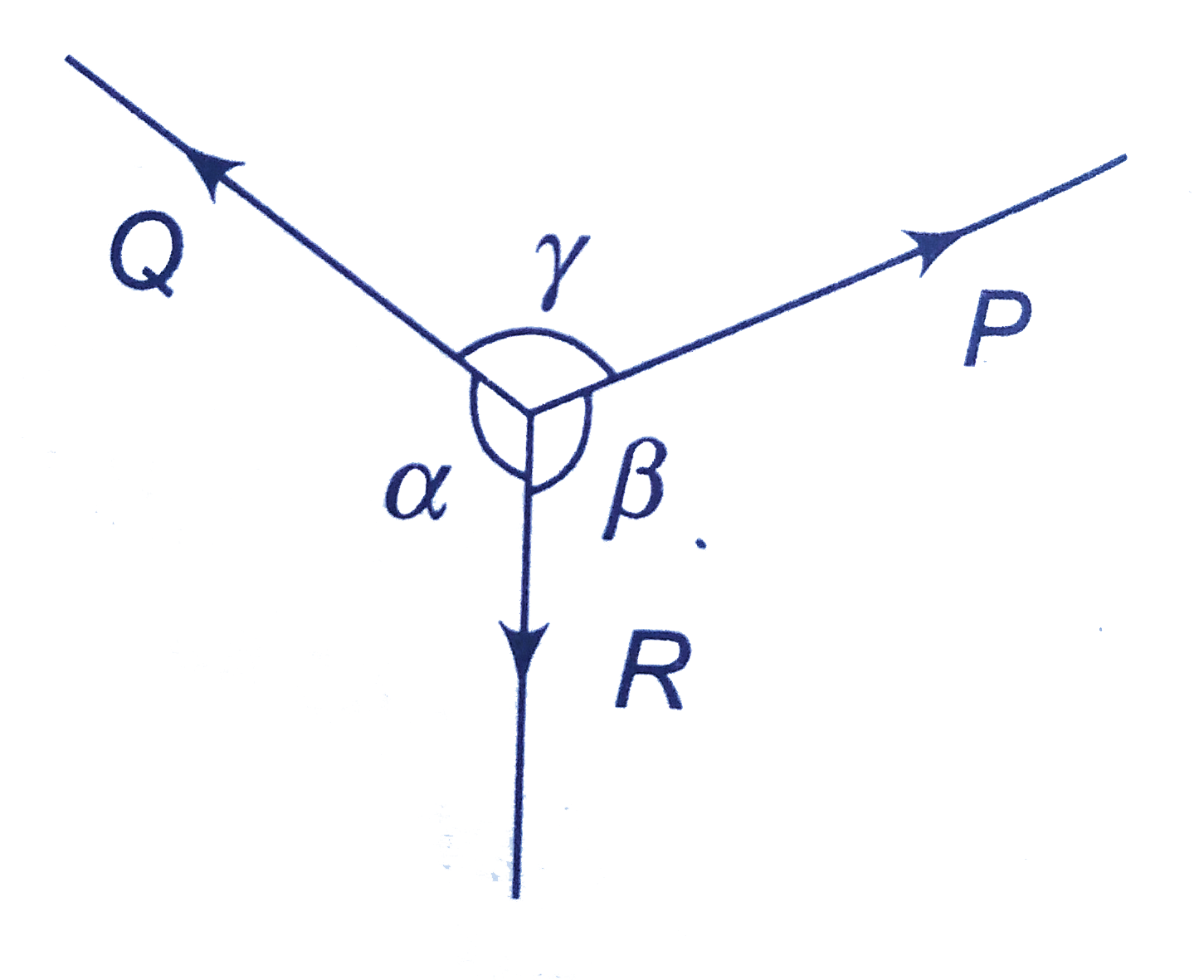 01:10View Solution
01:10View SolutionThree forces start acting simultaneously on a particle moving with velocity, `barv`. These forces are respresented in magnitude and direction by the three sides of a triangle ABC. The particle will now move with velocity
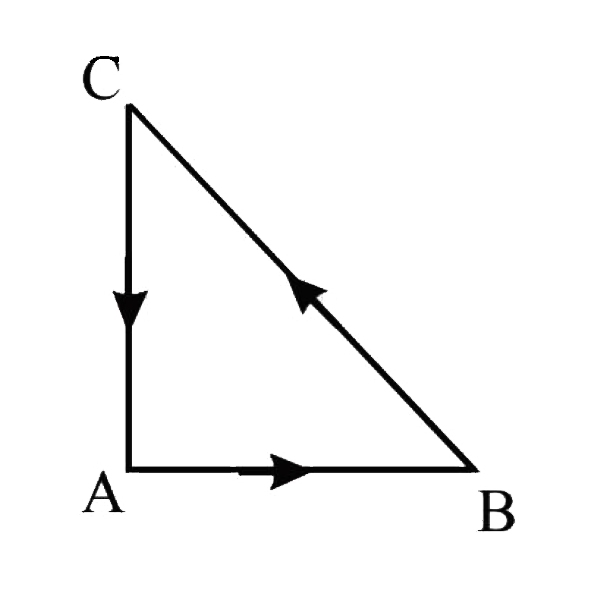 01:40View Solution
01:40View SolutionAs shown in figure the tension in the horizontal cord is `30 N`. The weight `W` and tension in the string `OA` in Newton are
 02:45View Solution
02:45View SolutionThe block is in equilibrium
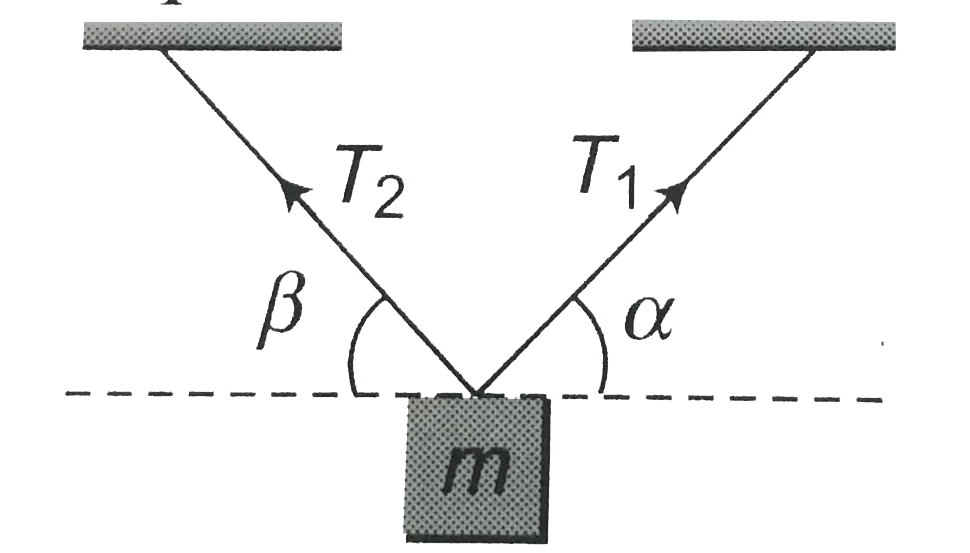
`(i) T_(1)=(mgcosbeta)/(sin(alpha+beta))" "(ii)T_(2)=(mgcosalpha)/(sin(alpha+beta))`
`(iii)T_(1)/T_(2)=(cosbeta)/(cosalpha)" "(iv)T_(1)/T_(2)=(cosalpha)/(cosbeta)`02:51View SolutionA metal sphere is hung by a string fixed to a wall. The sphere is pushed away from the wall by a stick. The forces acting on the sphere are shown in the second diagram. Which of the following statements is wrong?
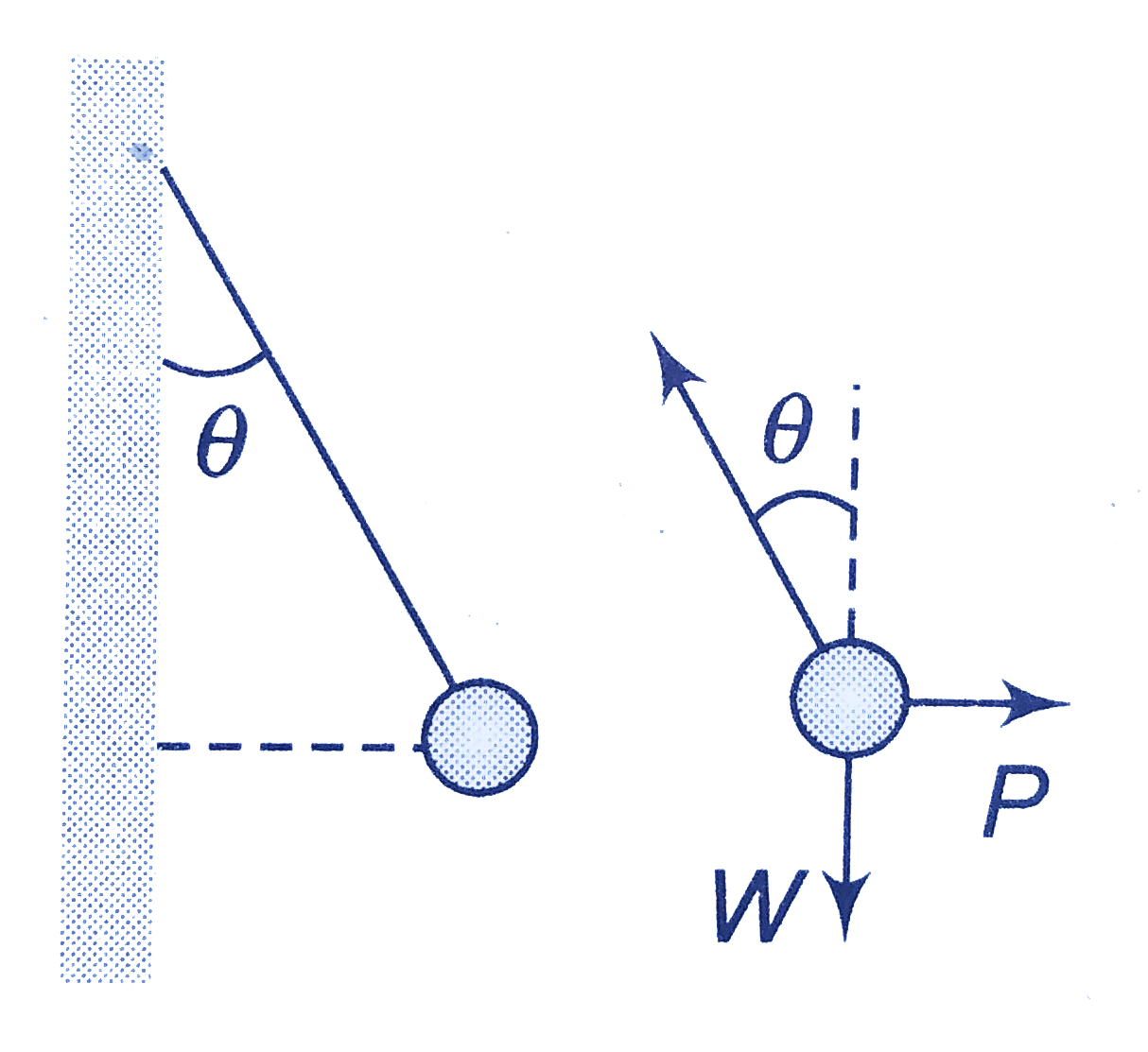 03:28View Solution
03:28View SolutionWhen forces `F_(1)` , `F_(2)` , `F_(3)` are acting on a particle of mass m such that `F_(2)` and `F_(3)` are mutually prependicular, then the particle remains stationary. If the force `F_(1)` is now rejmoved then the acceleration of the particle is
03:58View SolutionThe pulleys and strings shown in the figure are smooth and of negligible mass. For the system to remain in equilibrium, the angle `theta` should be
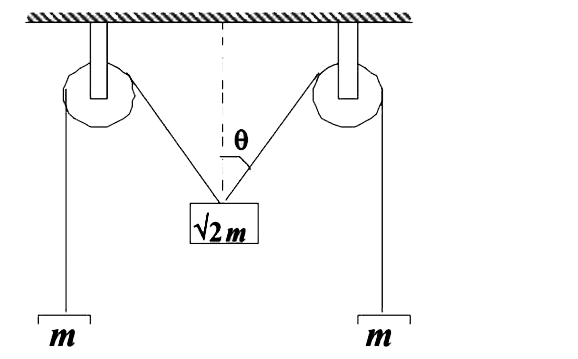 03:00View Solution
03:00View SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with a horizontal accelertion a. The angle made by the string with verical is
01:24View SolutionIf a body is in equilibrium under a set of non-collinear forces, then the minimum number of forces has to be
02:03View SolutionThe acceleration of light pulley is
 04:22View Solution
04:22View SolutionConsider the situation as shown in the firgure.
 04:11View Solution
04:11View SolutionThe acceleration of the block A is
 02:46View Solution
02:46View SolutionThe acceleration of the block A and B are
 02:47View Solution
02:47View SolutionThe acceleration of the block A and B are
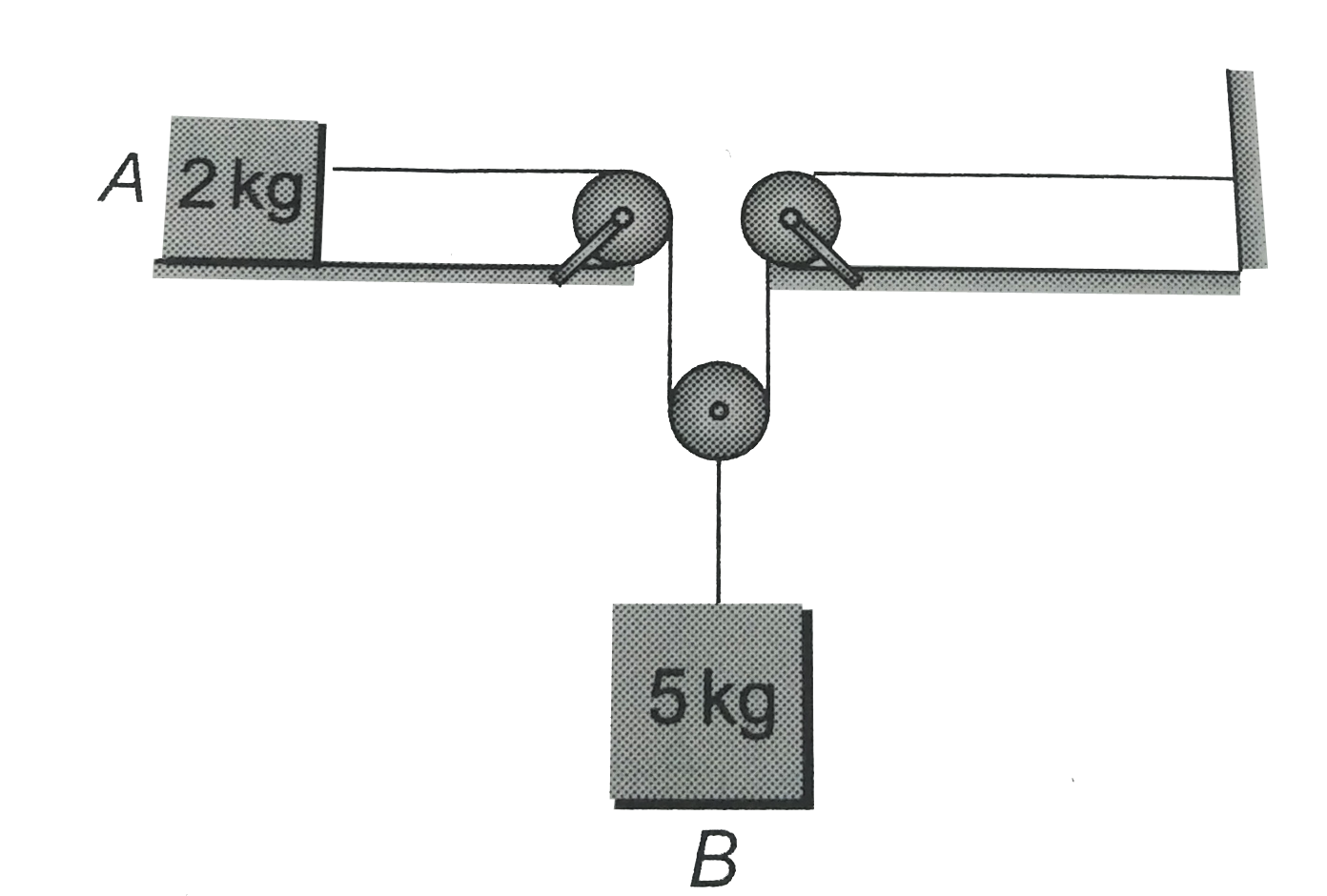 02:04View Solution
02:04View SolutionThe acceleration of m is
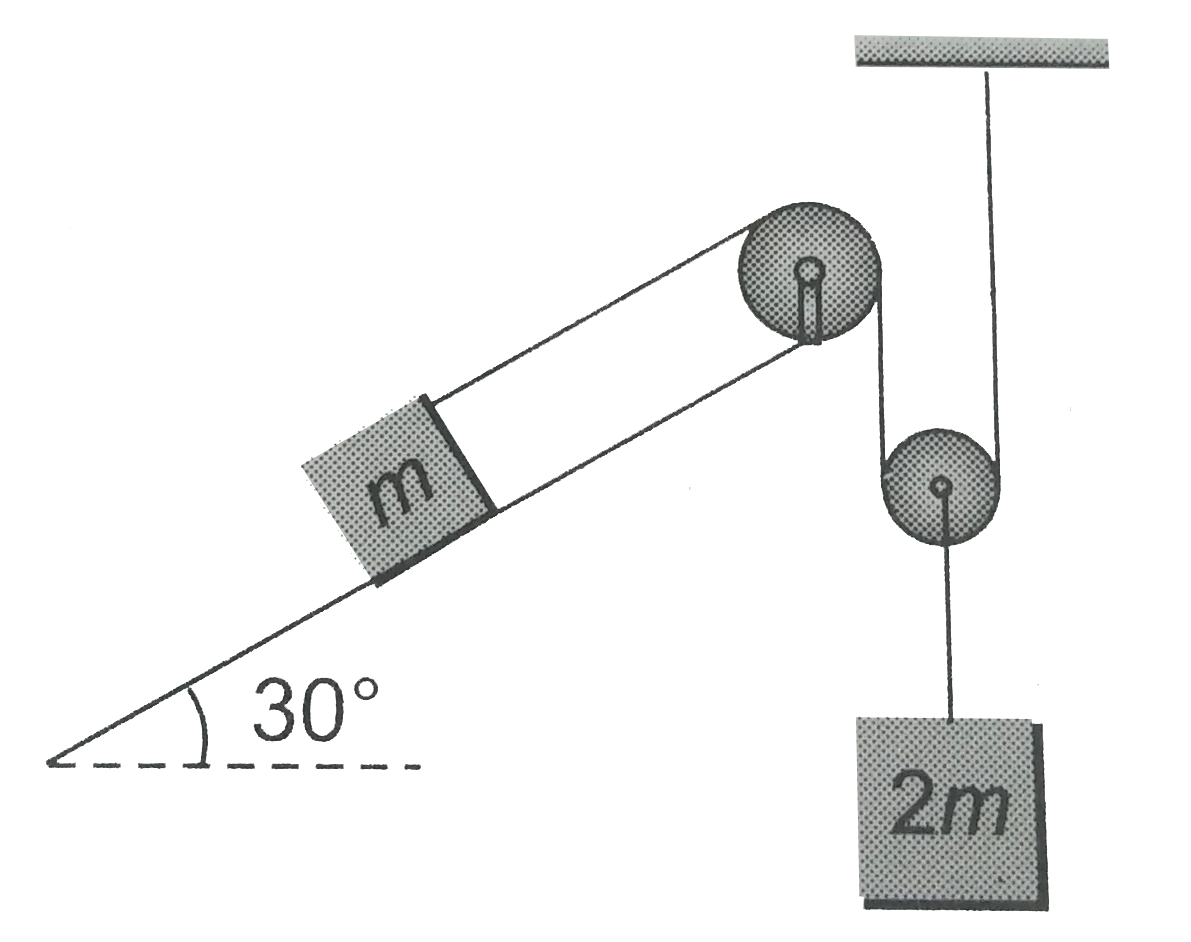 02:40View Solution
02:40View SolutionIn the arrangement shown in the Fig, the ends P and Q of an unstretchable string move downwards with uniform speed U. Pulleys A and B are fixed.
Mass M moves upwards with a speed
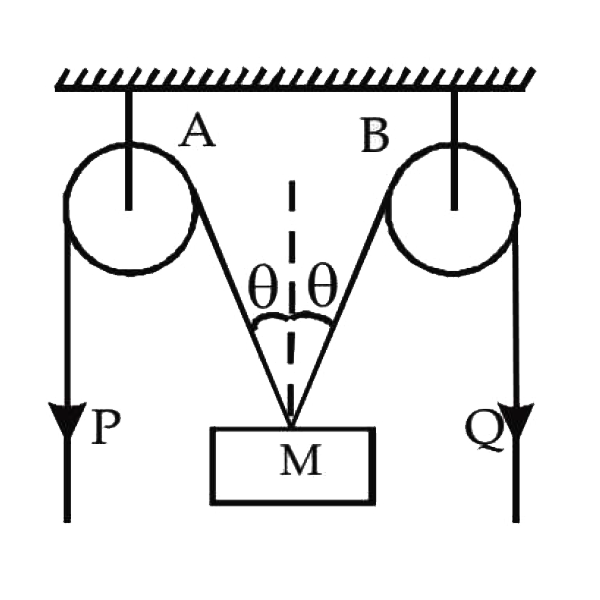 06:41View Solution
06:41View SolutionIn the figure, the blocks are of equal mass. The pulley is fixed. In the position shown. A moves down with a speed u and `v_(B)=` the speed of B.
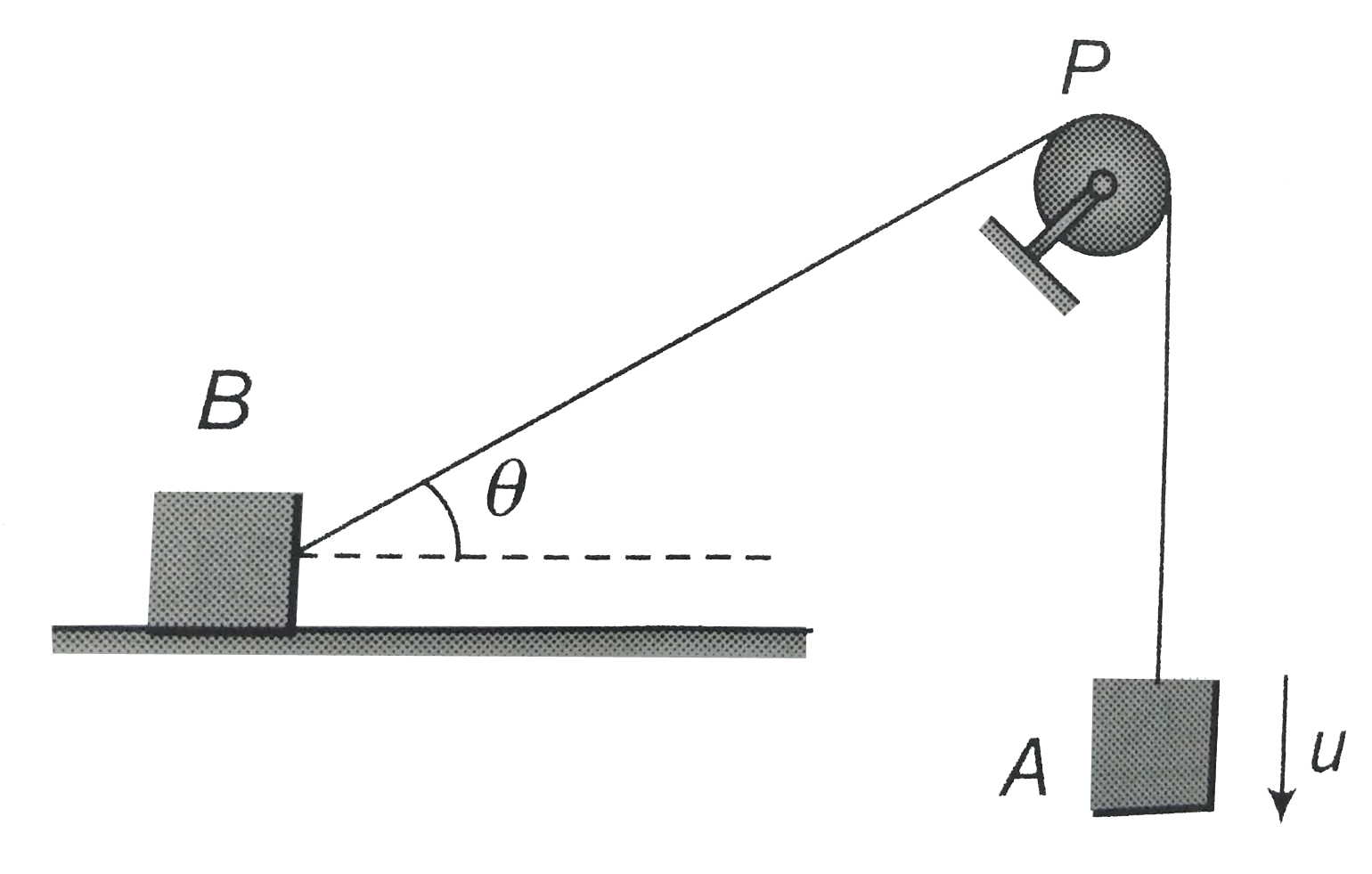
(i) B will never lose contact with the ground.
(ii) The downward acceleration of A is equal in magnitude to the horizontal acceleration of B
(iii) `v_(B)=ucostheta` (iv) `v_(B)=u//costheta`03:29View SolutionA spring fo spring constant k is broken in the length ratio 1:3. The spring constant of larger part will be
01:53View SolutionA block of mass 10 kg is suspended through two light spring balances as shown in figure
 02:30View Solution
02:30View SolutionIn the arrangement shown, the pulleys are fixed and ideal, the strings are light, `m_(1)gtm_(2)` and S is a spring balance which is itself massless. The readings of S (in units of mass) is
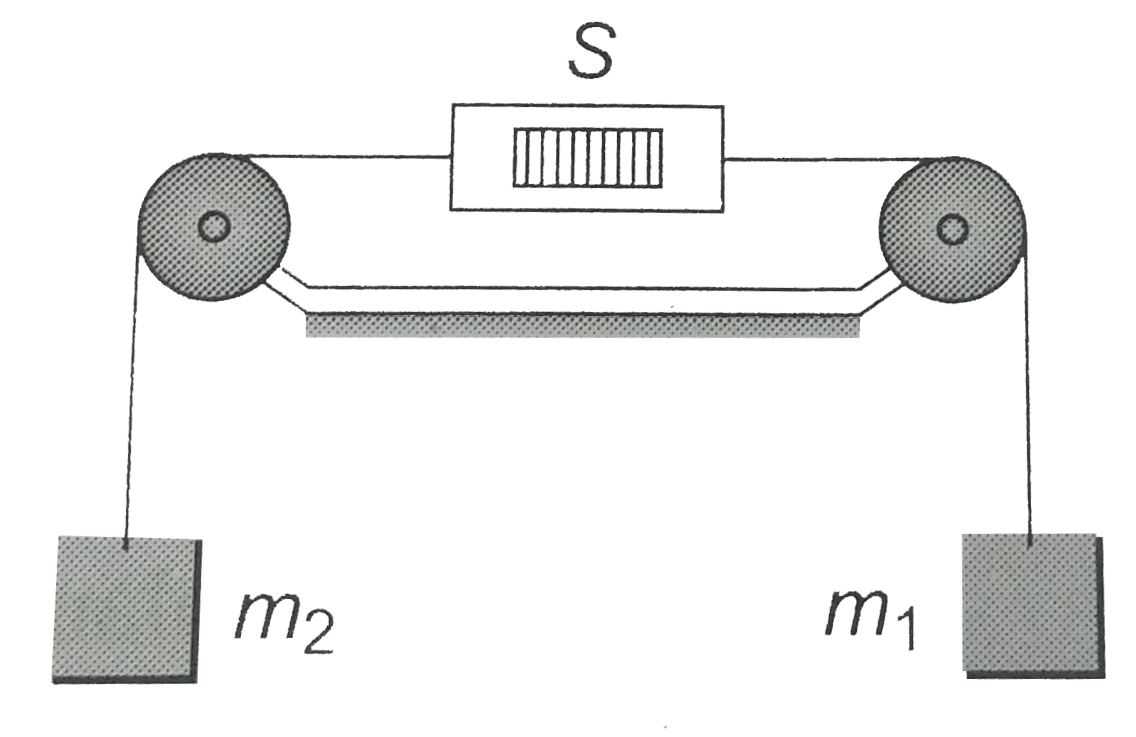 02:22View Solution
02:22View SolutionTwo blocks A and B of masses 2m and respectively, are connected by a massless and inextensible string. The whole system is suspended by a masslessspring as shown in the figure. The magnitude of acceleration of A and B, immediately after the string is cut, are respectively
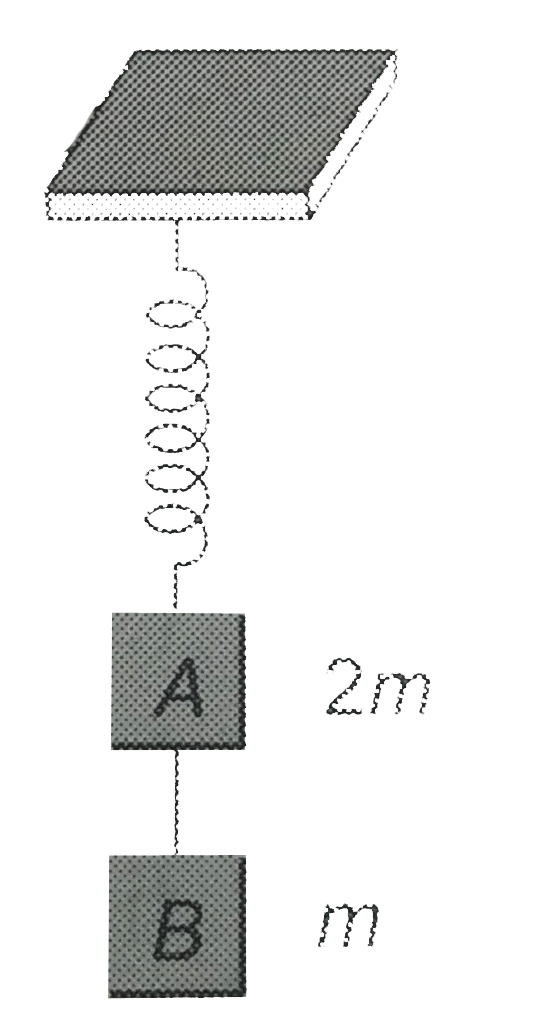 02:33View Solution
02:33View SolutionThe masses of 10 kg and 20 kg, respectively, are connected by a light spring as shown in the figure. A force of 200 N acts upon the 20 kg mass. At the instant shown, the 10 kg mass the acceleration of `12m//s^(2)`. The acceleration of 20 kg mass is
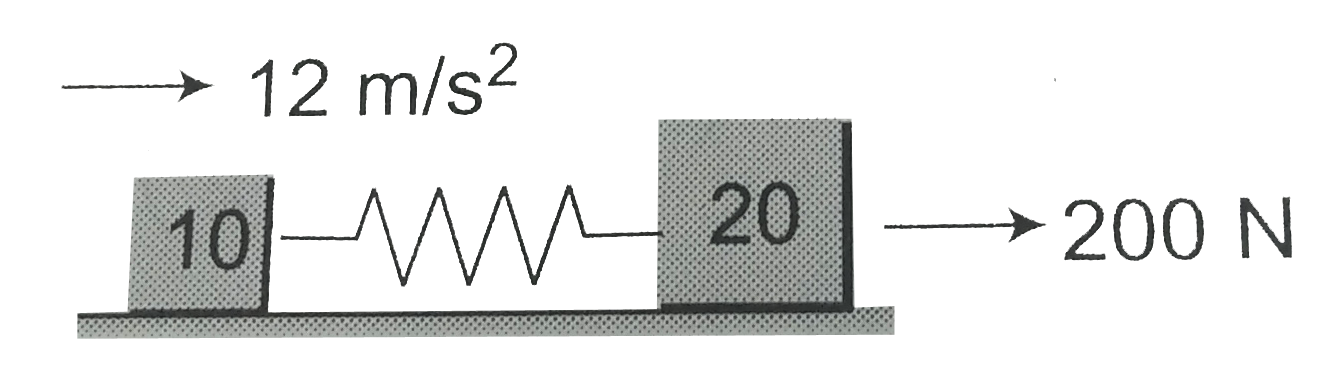 01:36View Solution
01:36View SolutionFor ordinary terrestrial experimants, the observer is an inertial frame in the following cases is
02:08View SolutionA reference frame attached to the earth
02:36View SolutionA balloon with mass `m` is descending down with an acceleration a `(where altg)` . How much mass should be removed from it so that it starts moving up with an acceleration a?
05:16View Solution
EXERCISES questions and complete solutions for chapter NEWTONS LAWS OF MOTION of CP SINGH PHYSICS (HINGLISH) of Class 11
