Complete Solutions to EXAMPLES of chapter NEWTONS LAWS OF MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | NEWTONS LAWS OF MOTION |
| CP SINGH | EXAMPLES |
| Number Of Questions | 65 |
| Academic Year | 2023-24 |
A block of mass `5` kg is acted upon two perpendicular force `7` N and `24N`. Find the magnitude and the direction of acceleration of the block.
02:55View SolutionThree forces `vec(F_(1))=23hat(j)+3hat(j)-hat(k), vec(F_(2))=4hat(i)-hat(j)-2hat(k)` and `vec(F_(3))=23hat(j)+3hat(k)N`act on a block of mass `5kg`. Calculate the acceleration of the particle.
02:23View SolutionA constant force acting on a block of mass `5` kg changes `(a)` its speed from `6m//s` to `10 m//s` in travelling a distance `8m` in a straight line, (b) its speed from `2m//s` to `8m//s` in `3s` a straight line. Find the magnitude and the direction of the force.
02:53View SolutionTwo blocks are attached by a light inextensible string and the system is pulled by applying a force `F_(0)` as shown in the diagram. Find the acceleration of each block and tension in the string.
 04:40View Solution
04:40View Solution
Find the common acceleration and tension in each string.04:20View SolutionThe blocks are attached by an inextensible light string and pulled vertically upward by force `100N` as shows. Find the common acceleration and tension in the string
 02:50View Solution
02:50View SolutionThe blocks of masses `2kg, 3kg` and `5kg` are connected by light inextensible strings as shown. The system of blocks is raised vertically upwards by appling a force `F_(0)=200N`. Find the common acceleration and tensions in the strings.
 05:31View Solution
05:31View SolutionIn the arrangement shown, find the acceleration of each block, tension in the string and reaction in the pulley. The string and pulley are light (massless) `(m_(1)gtm_(2))`. Neglect the friction in pulley.
 05:03View Solution
05:03View SolutionThe pulley is light and smooth`:` the strings are inextensible and light. The system is released from rest, find the acceleration of each block, tensions in the strings and reaction in pulley.
 05:05View Solution
05:05View SolutionTwo blocks are connected by an inextensible light string, the string is passing over smooth, light pulley as shown. Find the acceleration of blocks and tension in the string, reaction in pulley.
 05:30View Solution
05:30View SolutionThe strings are inextensible and light`:` the pulleys are smooth and light. Find the acceleration of each block and tensions in the strings.
 08:29View Solution
08:29View SolutionA block is released on an smooth inclined plane of inclination `theta`. After how much time it reaches to the bottom of the plane?
 04:00View Solution
04:00View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.
 03:35View Solution
03:35View SolutionIn the arrangement shown, inclined plane is smooth, strings and pulleys are massless. Find `T_(1)/T_(2)`
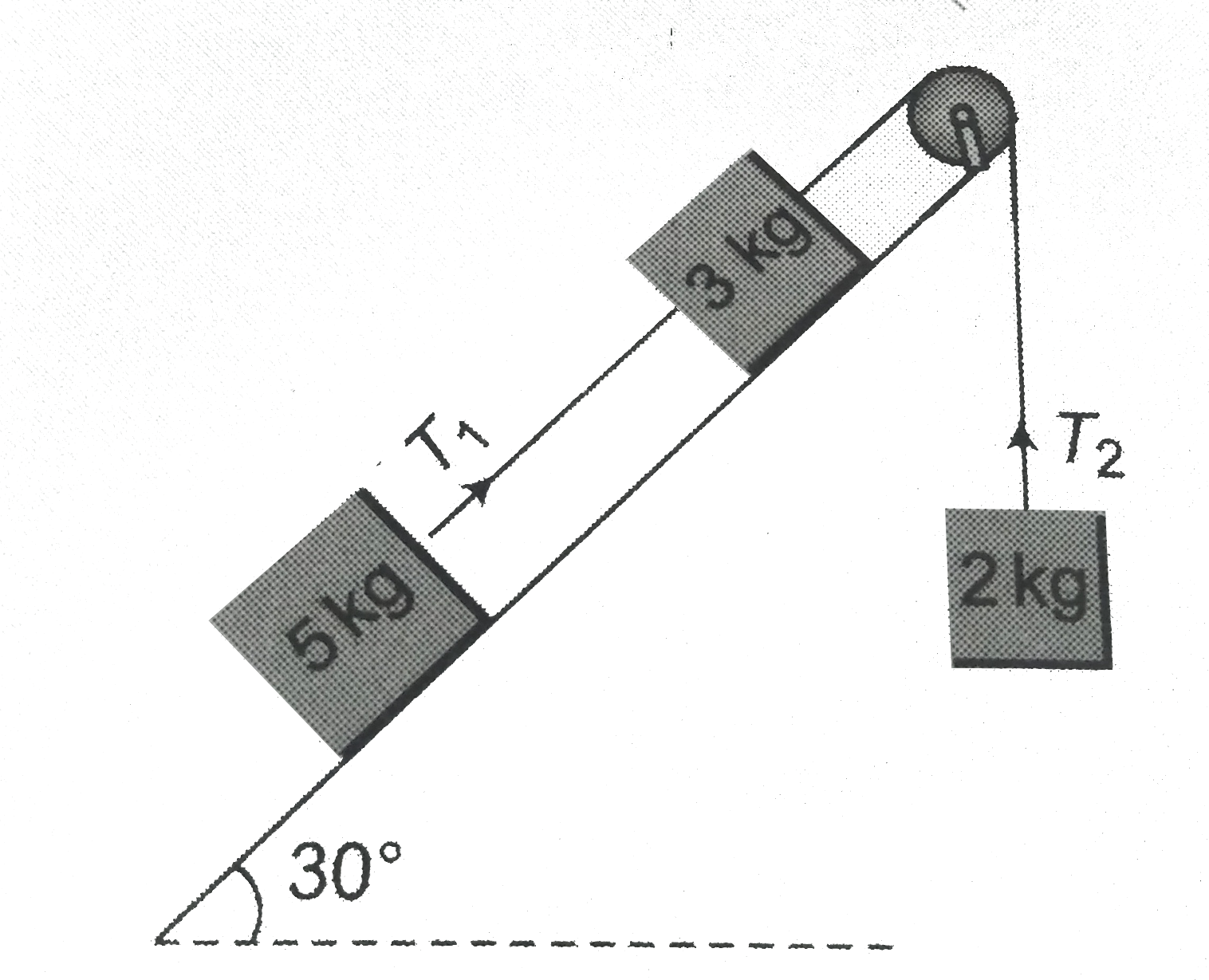 04:33View Solution
04:33View SolutionIn the arrangement shown, all the surfaces are smooth, strings and pulleys are light. Find the tension in the string.
`(CPS_V01_C06_S01_015_Q01.png" width="80%">03:32View SolutionA uniform rope of length of length `L` is pulled by a force `F` on a smooth surface. Find tension in the rope at a distance `x` from the end where force is applied.
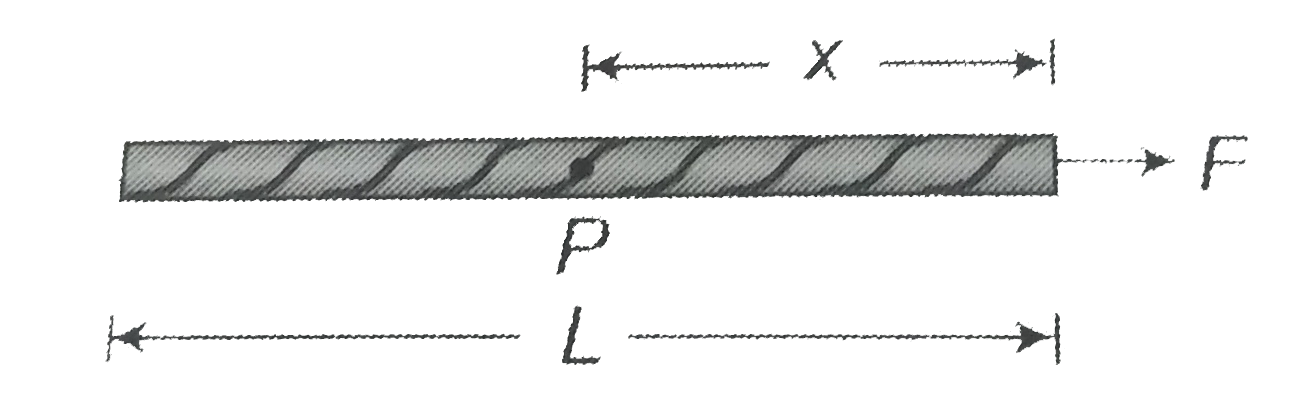 02:15View Solution
02:15View SolutionA block of mass `M` is attached to a uniform rope of mass `m`. This arrangement is pulled by applying a force `F` at the rope as shown. Find the tension in the rope (a) at the junction of the rope and the block (b) at the mid point of the rope.
03:36View SolutionTwo blocks of mass 2.9 kg and 1.9 kg are suspended from a rigid support S by two inextensible wires each of length 1 meter, see fig. The upper wire has negligible mass and the lower wire has a uniform mass of `0.2kg//m`. The whole system of blocks wires and support have an upward acceleration of `0.2m//s^2`. Acceleration due to gravity is `9.8m//s^2`.
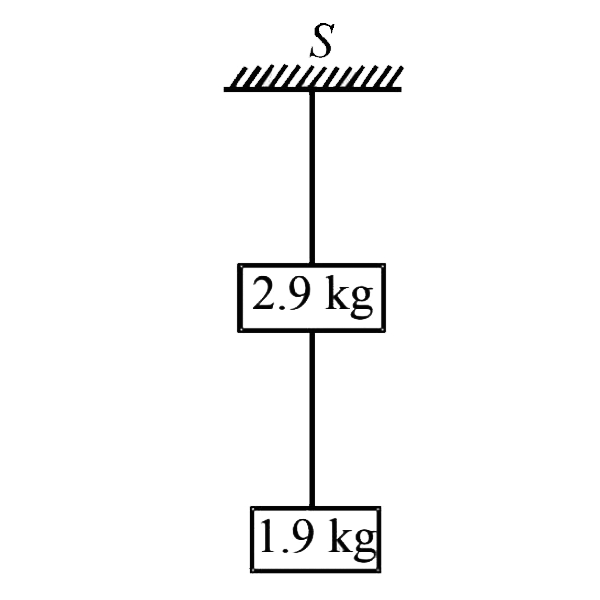
(i) Find the tension at the mid-point of the lower wire.
(ii) Find the tension at the mid-point of the upper wire.07:33View SolutionA uniform rope of mass `m` and length `L` is attached to the ceiling of a lift. The other end of the rope is attached to a block of mass `M`. The lift is moving up with a constant acceleration `a_(0)`. Find the tension in the rope at a distance `x` from the ceiling as shown in the diagram.
 02:49View Solution
02:49View SolutionTwo blocks of masses `m` and `2m` are placed on a smooth horizontal surface as shown in the figure. Find the acceleration of each block and normal reaction between two blocks if a horizontal force `F_(0)` is applied on (a) `m` and (b) `2m`
 04:13View Solution
04:13View SolutionThree blocks of masses `2kg,3kg` and `5kg` are placed in contact as shown in the diagram. A horizontal force of `30N` is applied on `2kg` block. Find the contact force between (a) `2kg` and `3kg` block and (b) `3kg` and `5kg` block.
 02:27View Solution
02:27View SolutionConsider the arrangement as shown in the figure. The lift is moving with acceleration `(g)//(4)` in vertically downward direction. Find the contact force (a) between the blocks (b) between the lower block and the floor of lift.
 02:47View Solution
02:47View SolutionConsider the situation as shown in the figure. The boy of mass `M` holds the light rope and the system is at rest. If `m` is mass of the box, find the force exerted by the boy on the rope and contact force beteween the boy and the box.
 03:20View Solution
03:20View SolutionIn the previous problem if `M=80kg` and `m=410kg` and the boy pulls the rope such that the system (boy+box) moves upward with acceleration `5m//s^(2)`,find the force exerted by the boy and contact force between the boy and the box.
03:38View SolutionA man of mass `60kg` is standing on a massless weighing machine. Find the weight of the man in different situations as shown in the following figures.

Man holds the rope and the block is at rest.

Man holds the rope and the system is at rest.
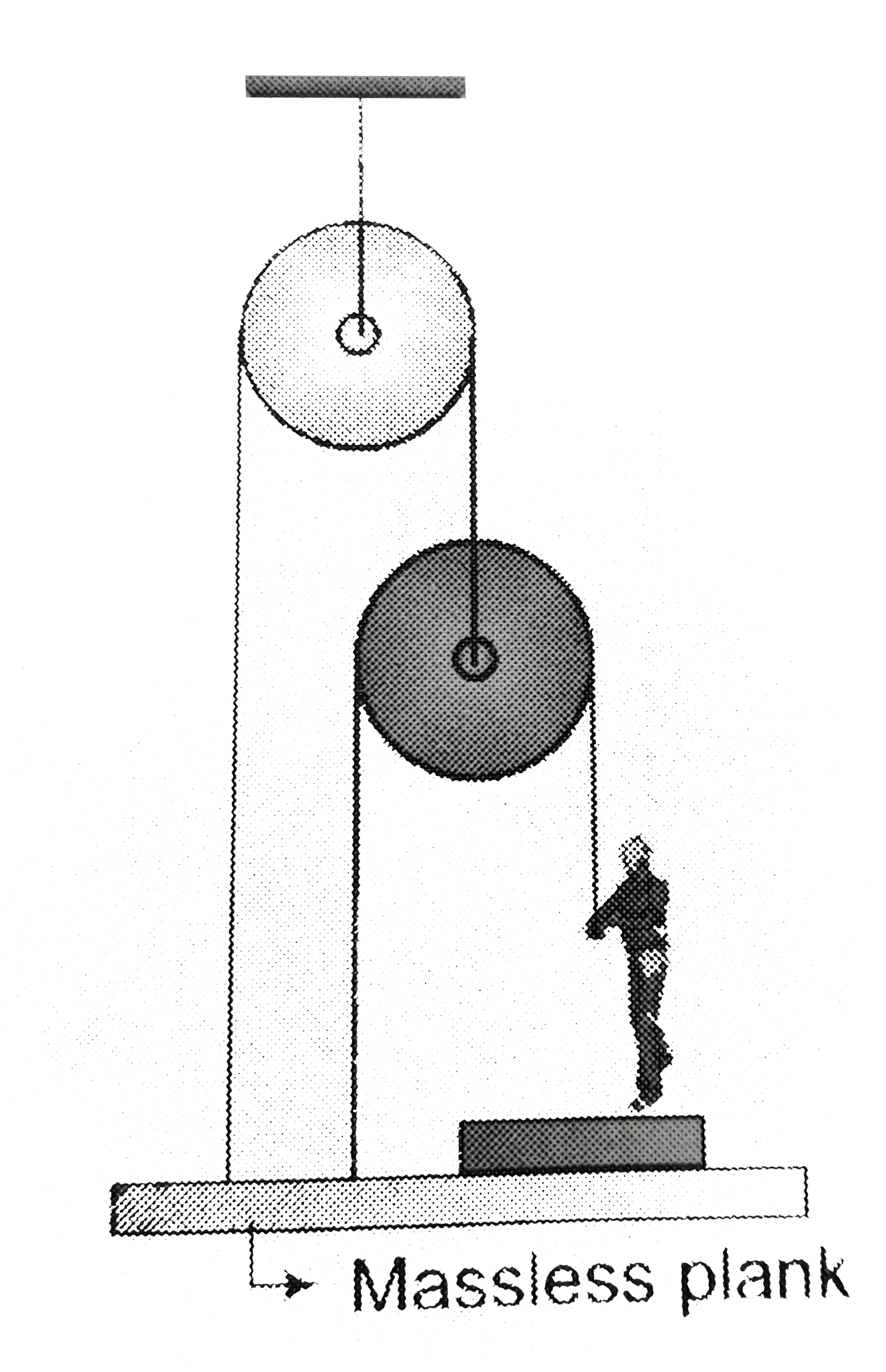
Man holds the rope and the system is at rest.07:03View SolutionA boy is standing on a weighing machine placed on the floor of an elevator. The elevator starts going down with some acceleration, moves with constant velocity for some time and finally decelerates to stop. The minimum and maximum weight recorded are `480N` and `840N` If the magnitude of reardation is double of acceleration, find (a) true weight of the boy and (b) magnitude of acceleration.
View SolutionA lift is going up. The total mass of the lift and the passengers is `2000kg`. The variation of speed of the lift is as shown in the diagram
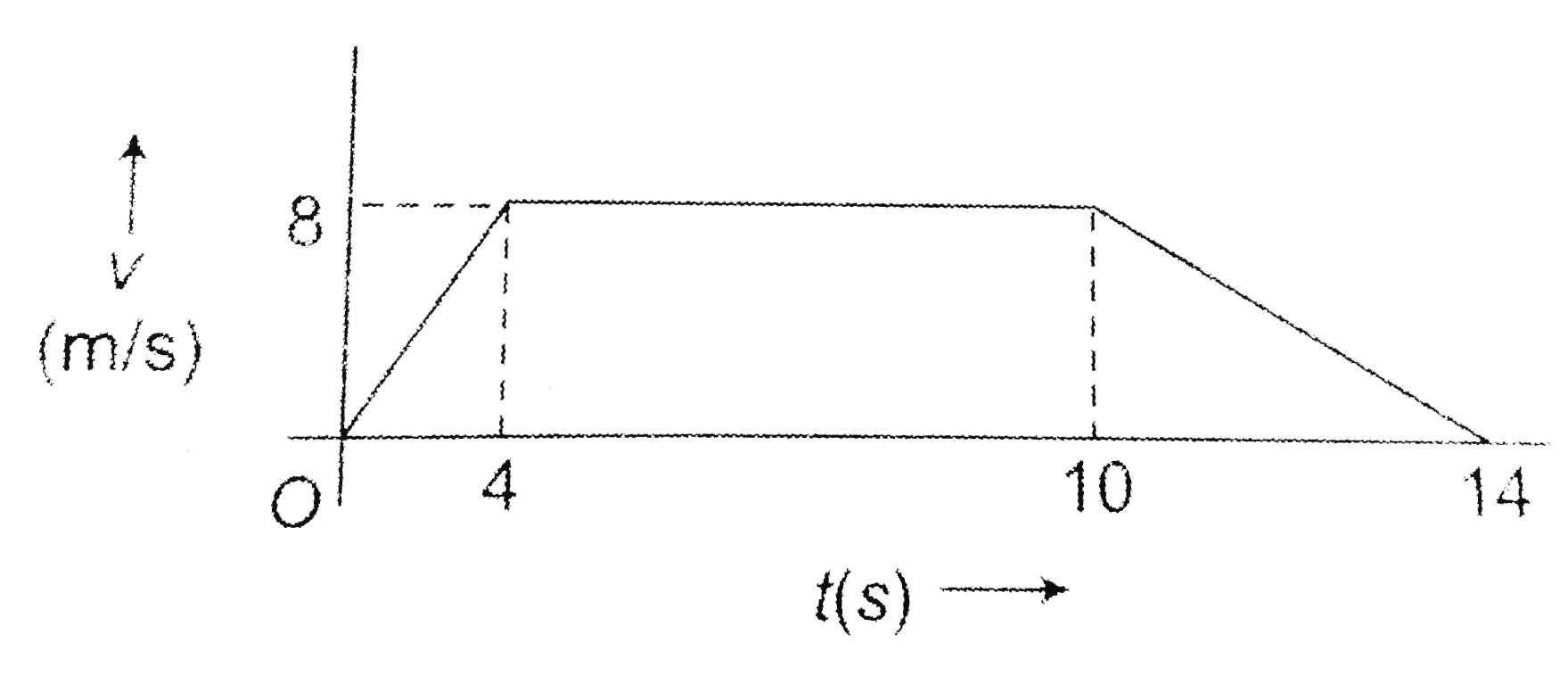
(a) What will be the tension in the rope pulling the lift at time equal to (i) `1s` (ii) `6s` (iii) `12s`? (b) What will be the average velocity and average acceleration during motion?05:38View SolutionA block of mass `m` is placed on a smooth wedge of inclination `theta`. The while system is acceleration horizontally so that the block does not slip. Find (a) horizontal acceleration, (b) normal force between the block and the wedge and (c) the horizontal force applied on the wedge.
03:52View SolutionConsider the situation as shown in the figure. All the surface are smooth and the string and pulley are light. Find the mass of the hanging block which will prevent the smaller block form slipping over the triangular block.
 11:19View Solution
11:19View SolutionA particle slides down a smooth incline of inclination `37^(@)`, fixed in an elevator going up with an acceleration `(g)//3`. The base of incline has a length `5m`. Find the time taken by the particle to reach the bottom.
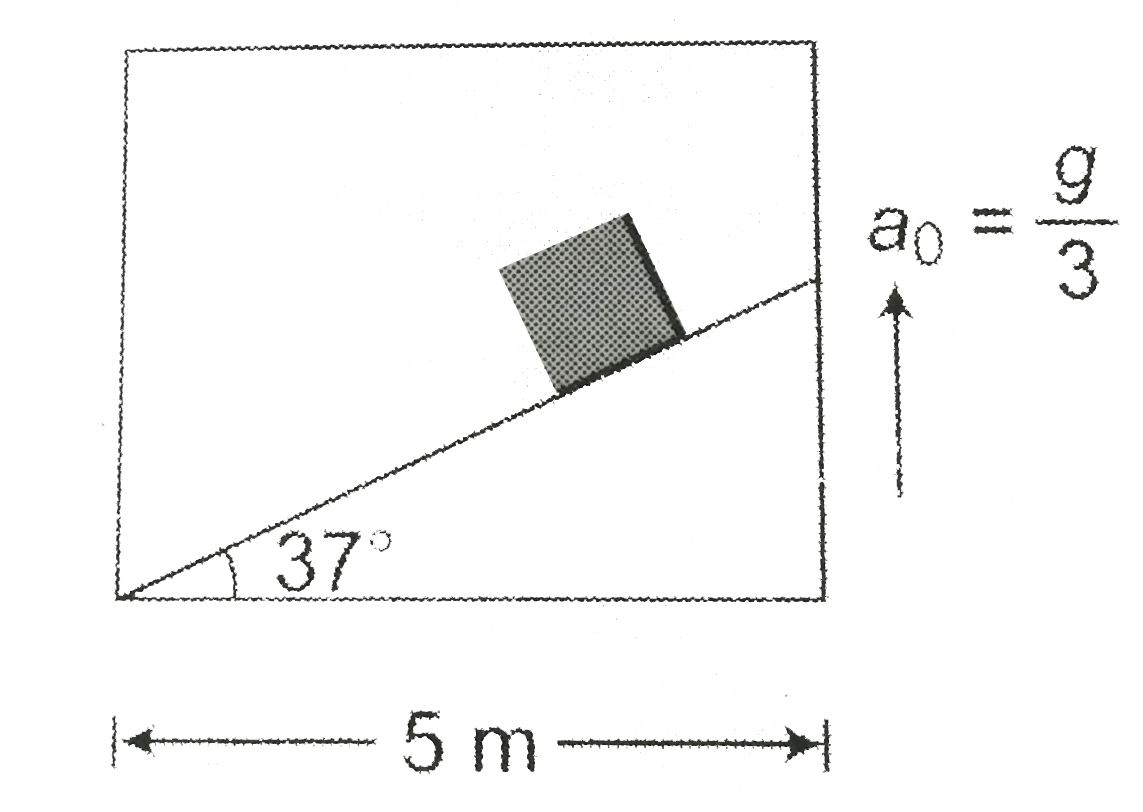 03:43View Solution
03:43View SolutionA pendulum is hanging from the ceiling of a car having an acceleration `a_(0)` with to the road. Find the angle made by the string with the verical and tension in the string.
02:35View SolutionA pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the loads of masses `3m` and `m` . The car starts gong up with acceleration `g//s`. Assuming the masses of the pulley and the thread, as well as friction, to be negligible, find the force exerted by the pulley on the ceiling of car.
 04:10View Solution
04:10View SolutionIn the arrangement shown in the figure, the blocks have masses `3m,m` and `2m`, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass `3m`.
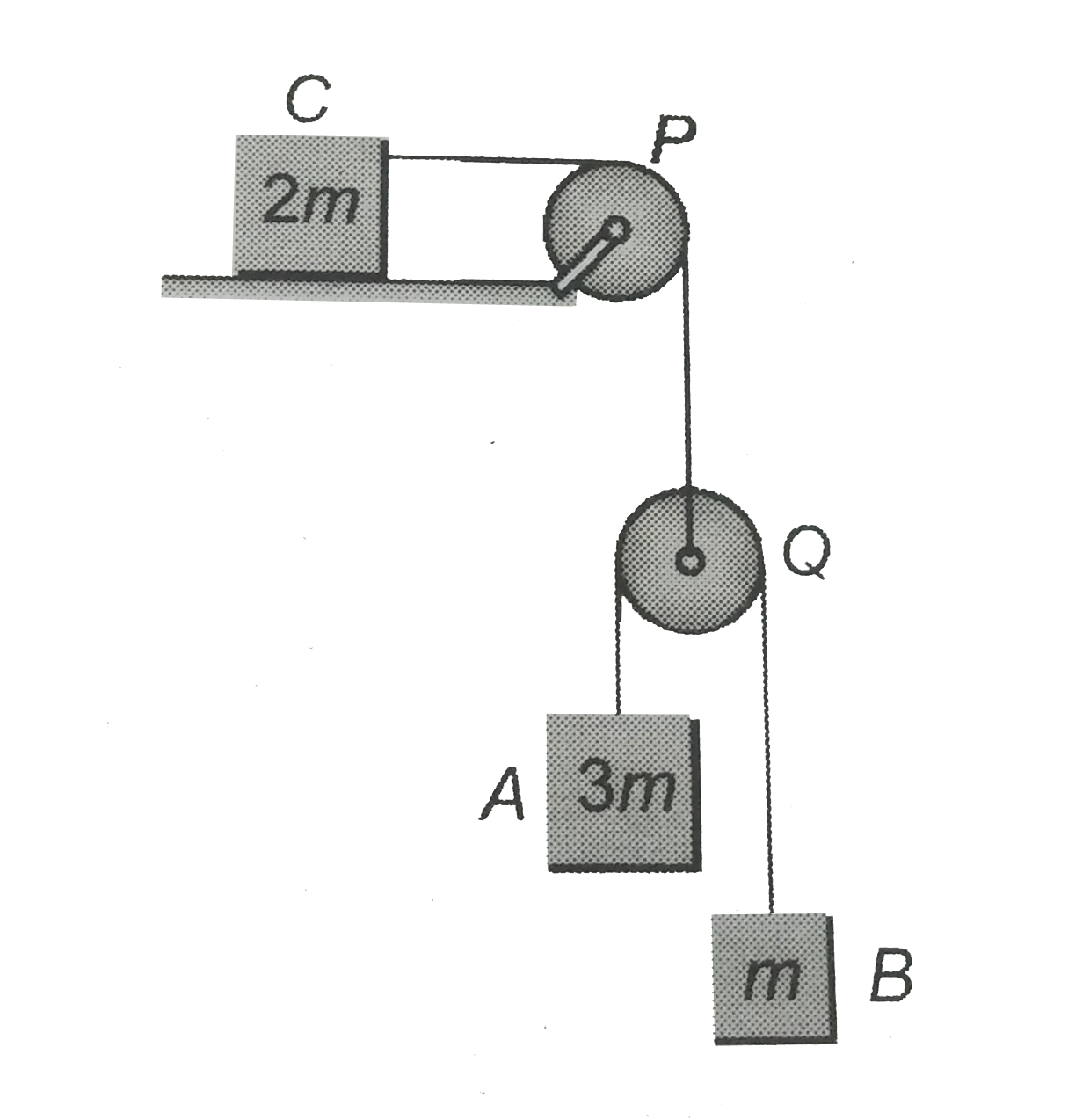 08:08View Solution
08:08View SolutionConsider the arrangement shown in the figure. Find the acceleration of the block
(a) A monkey moves upward with respect to the rope with acceleration `a_(0)`
(b) A monkey moves downward with respect to the rope with acceleration `a_(0)`
Assume the surface smooth, pulley and string light.
 03:02View Solution
03:02View SolutionAssuming all the surfaces to be smooth, find the acceleration of the triangular block of mass `M` when the block of mass `m` slides on it.
 04:47View Solution
04:47View SolutionWith what minimum acceleration can monkey slide down a rope whose breaking strength is two third of his weight?
01:00View SolutionA block of mass `m` is attached to a chain as shown in the diagram. Find the tension in each of the three chains. The ring and chains are light.
 01:32View Solution
01:32View SolutionA block of mass `M` si suspended by two strings angles `theta_(1)` and `theta_(2)` with the horizontal. Find the tensions in the strings.
 03:03View Solution
03:03View SolutionThe blocks are in equilibrium with a constant horizontal force `2mg` acting on block `B`. The strings are light, find tensions in the strings and values of angles `alpha` and `beta`
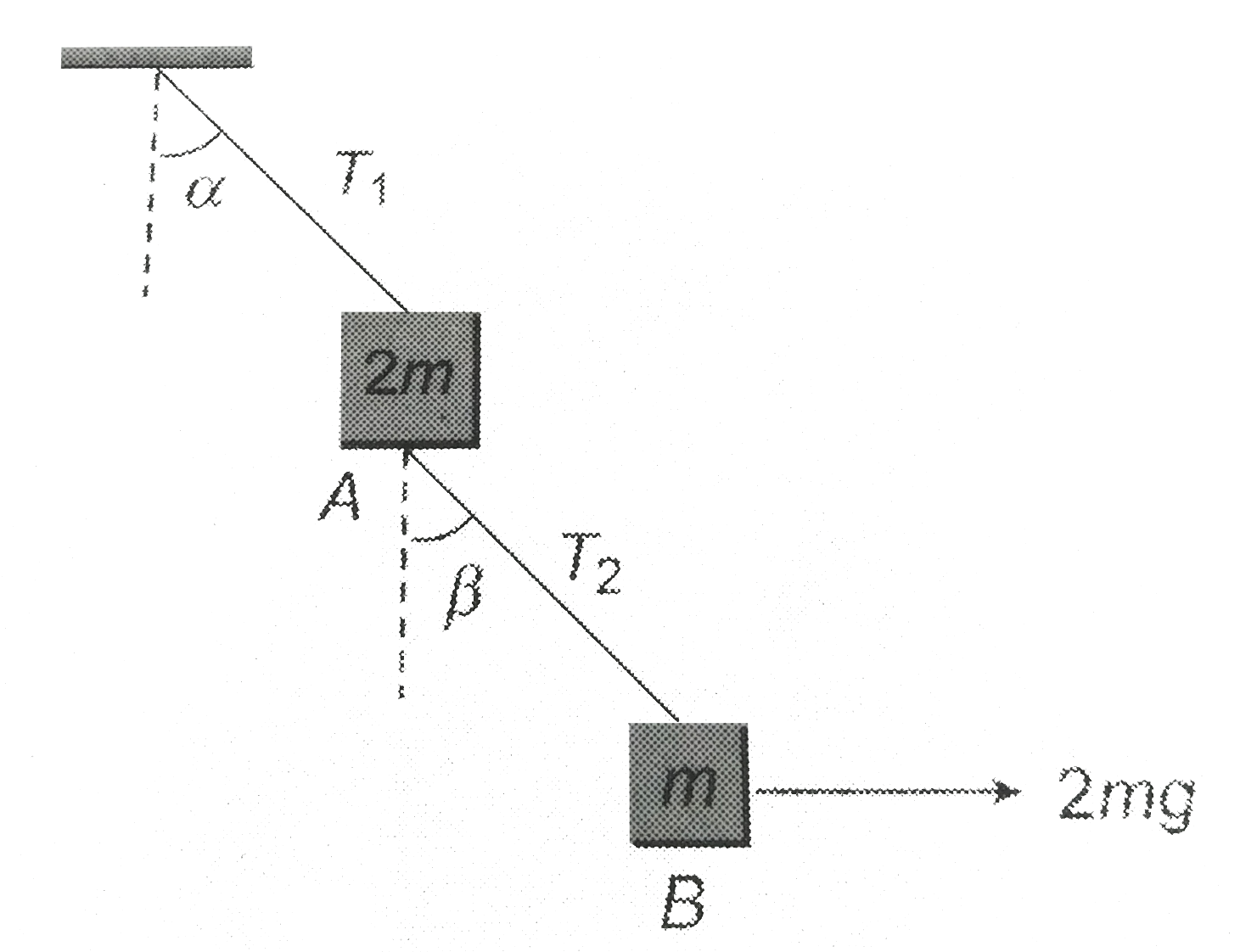 06:26View Solution
06:26View SolutionTwo masses `m_(1)` and `m_(2)` are attached with light strings as shown. If the system is in equilibrium, find the value of `theta`
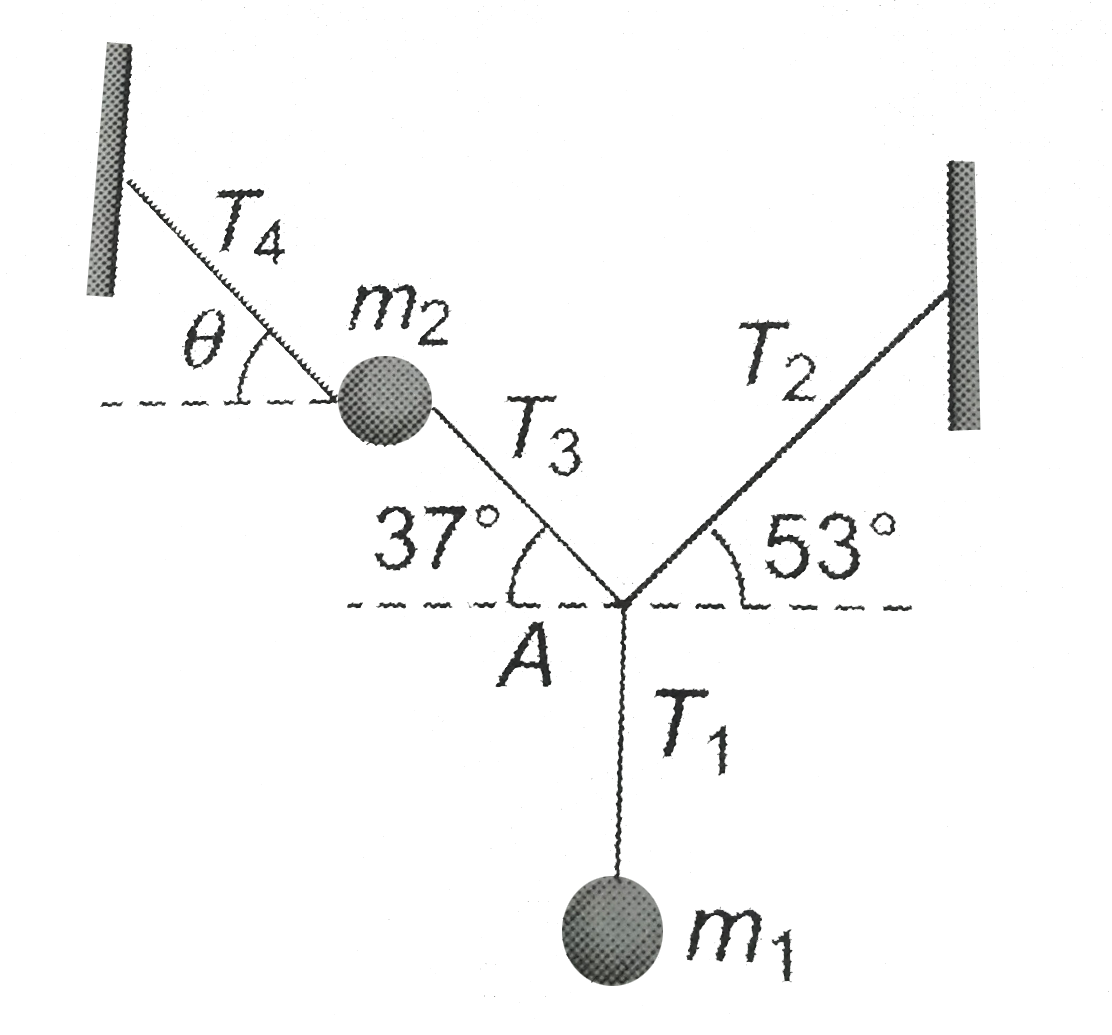 04:34View Solution
04:34View SolutionA balloon carring some sand is moving down with a constant acceleration `a_(0)`. How much mass of sand should be removed, so that the balloon move up with same acceleration?
02:39View SolutionA block is kept the floor of an elevator at rest. The elevator starts descending with an acceleration of `12m//s^(2)`. Find the displacement of the block during the first `1s` after the start.
View SolutionA block is pulled slowly as shown in the diagram. Show that force `F` increase as the block moves up. Find the force `F` when the block is at depth `h`.
 03:53View Solution
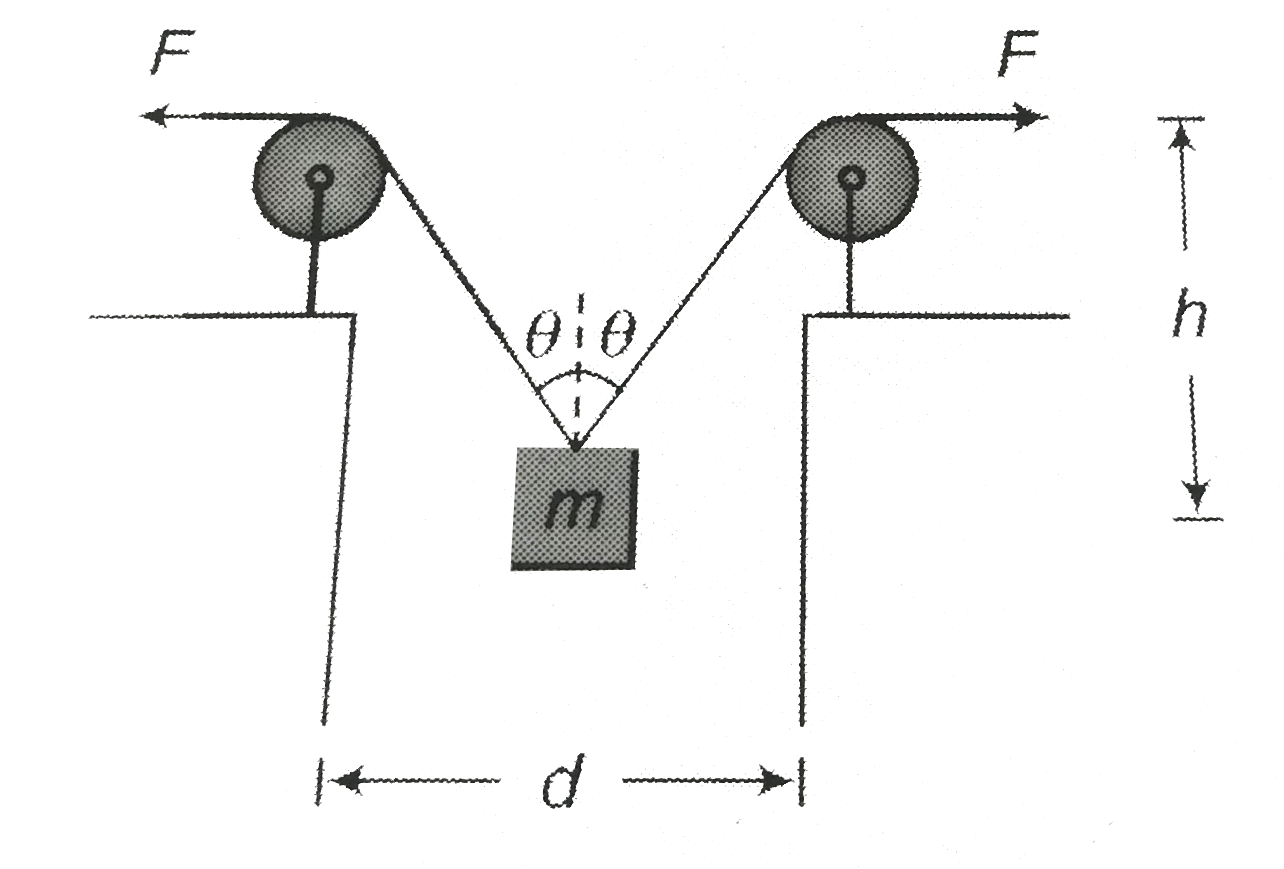
03:53View SolutionTwo particles each of mass `m` are connected by a light string of length `2L` as shown in the figure. A constant force `F` is applied continuoulsly at the mid`-`point of the string at right`-`angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is `2x`
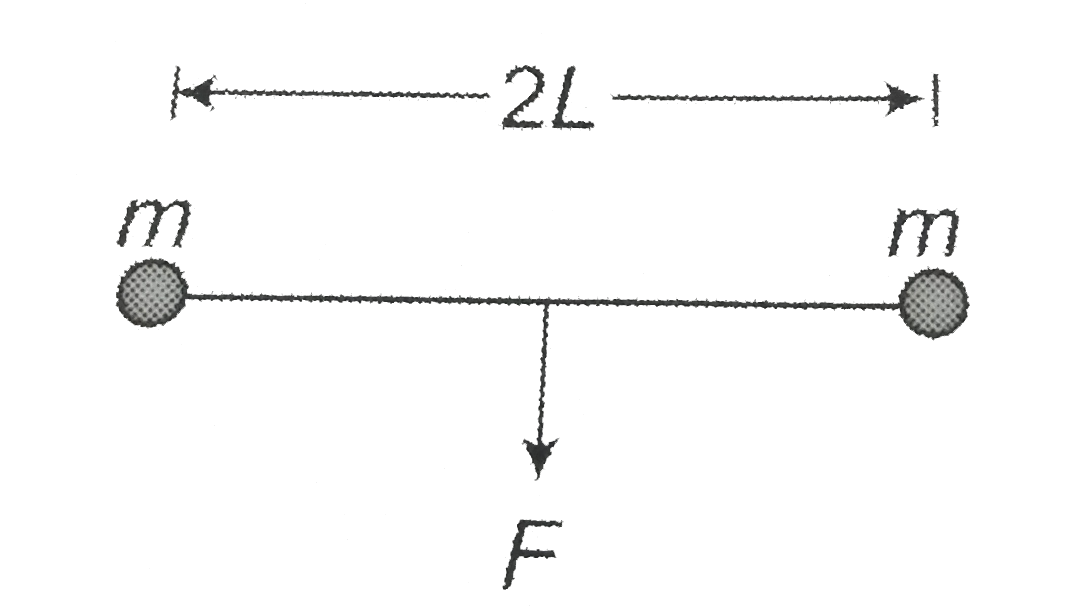 02:40View Solution
02:40View SolutionA uniform chain of mass `m` and length `l` is placed on a smooth table so that one`-`third length hanges freely as shown in the figure. Now the chain is released, with what velocity chain slips off the table?
 03:14View Solution
03:14View SolutionA block of mass `m` resting on a smooth horizontal plane starts moving due to a constant force `F=mg//3` of constant magnitude. In the process of its rectilinear motion the angle `theta` varies as `theta=lamdas`, where `lamda` is constant and `s` is the distance traversed by the block from its intial position. Find the velocity of the block as a function of the angle `theta`. Also show that the block will never lose contact with the ground.
View SolutionAt the moment `t=0` the force `F=at` is applied to a small body of mass `m` resting on a smooth horizontal plane (a is constant).
The permanent direction of this force forms an angle `alpha` with the horizontal (figure). Find:
(a) the velocity of the body at the moment of its breaking off the plane,
(b) the distance traversed by the body up to this moment.
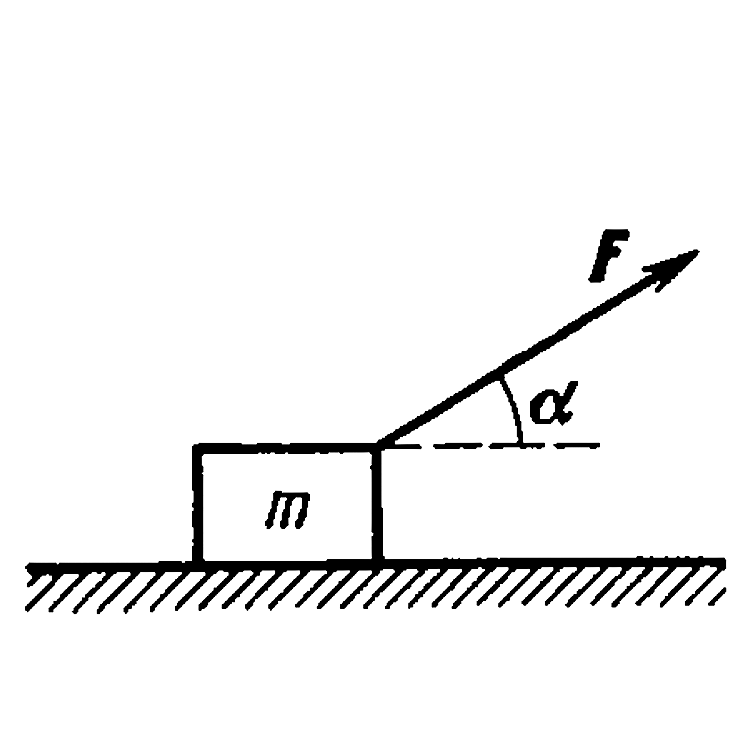 11:09View Solution
11:09View SolutionThe monkey `B` shown in the figure is holding on the tail of the monkey. A which is climbing up a rope. The masses of the monkeys `A` and `B` are `40kg` and `20kg`, respectively. If `A` can tolerate a tension of `300N` in its fail, what force should it apply on the rope in order to carry the monkey `B` with it?
 01:47View Solution
01:47View SolutionFind the acceleration of each block in the situation shown in the figure. All the surface are smooth and the pulleys and sttings are light.
 02:25View Solution
02:25View SolutionFind the acceleration of the block of mass `m` in the arrangement shown in the following figures. The masses of the pulleys and the threads, as well as the friction are assumed to be negligible.
 05:33View Solution
05:33View Solution
if a mass of ball is m/2 and that of a rod is m the length of the rod is 20 cm the ball is set on the same level as the lower end of the rod and then released. If pulleys and strings are light, friction negligible how soon will the ball be opposite top the upper end of the rod?04:48View Solution ltbr. Consider the situation as shown in the figure. Initially blocks are at rest o the floor. A constant upward force F is applied on the pulley Assuing the pulley smooth and light and the string massless, find the acceleration of each blocks and pullay if F is (a) 10N,
ltbr. Consider the situation as shown in the figure. Initially blocks are at rest o the floor. A constant upward force F is applied on the pulley Assuing the pulley smooth and light and the string massless, find the acceleration of each blocks and pullay if F is (a) 10N,
(b). 60 N
(c) 120 N
Given `m_(1)=2kg,m_(2)=4kg`05:17View Solution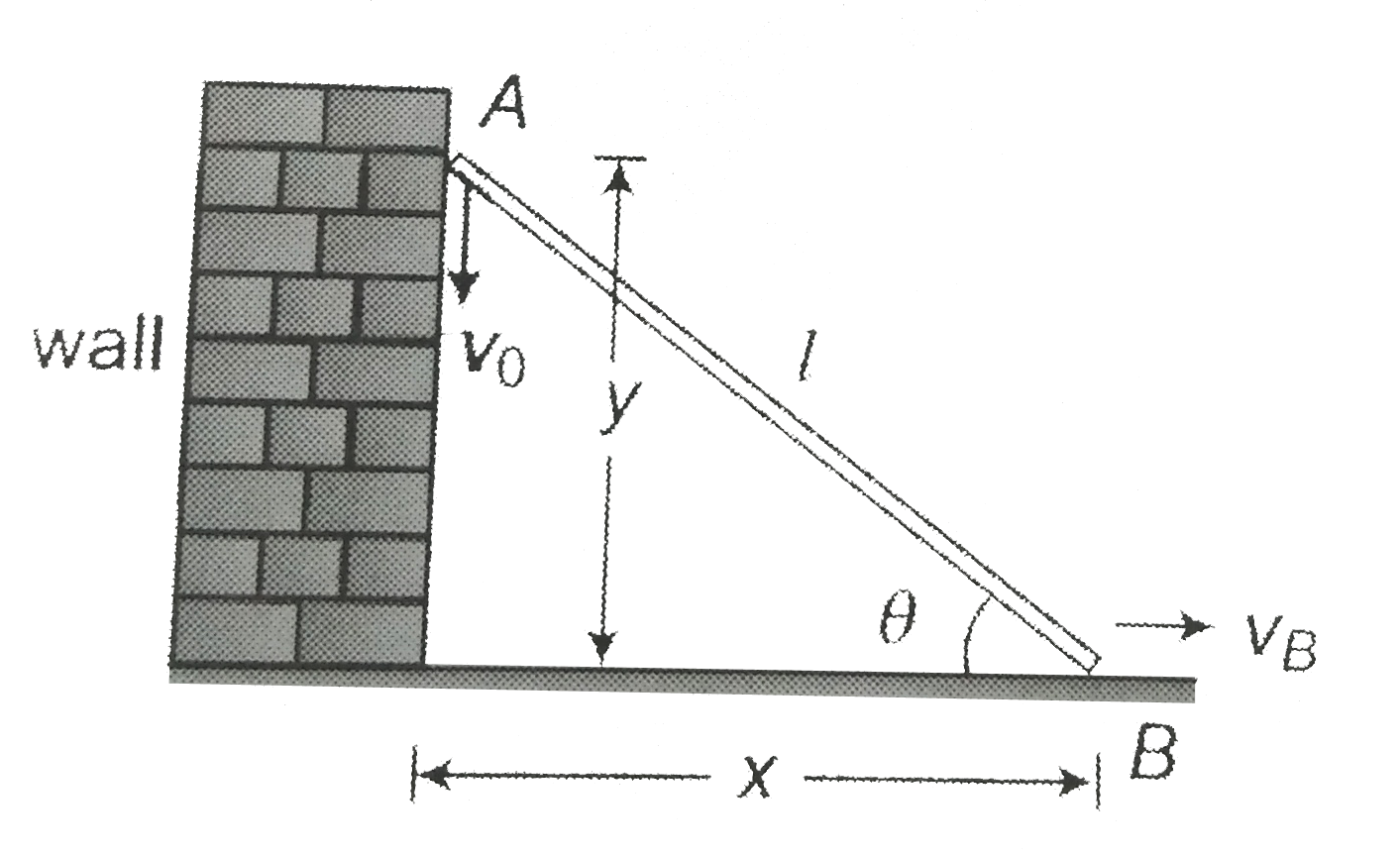
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is `v_(0)` in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle `theta ` with horizontal01:20View SolutionIn the arrangement shown in figure the ends P and Q of an inextensible string move downwards with uniform speed u. Pulleys A and B are fixed. The mass M moves upwards with a speed
 01:22View Solution
01:22View Solution
Two blocks are connected by an inextensible string as shown. The pulley is fixed. If block A moves down with speed v, find the velocit of block B at instant.01:16View Solution
The smooth ring A can slide on a fixed horizontal rod as shown the pulley is fixed. If some instant velocity of ring is v, find the velocity of block at that instant.01:22View Solution ltbgt Find the velocity of block B when ring A is moving downward with velocity v. 00:53View Solution
ltbgt Find the velocity of block B when ring A is moving downward with velocity v. 00:53View Solution
In the figure, the pulley P moves to the right with a constant speed `v_(0)`. If the velocity of B is v in downward direction, find the velocity of A.01:25View Solution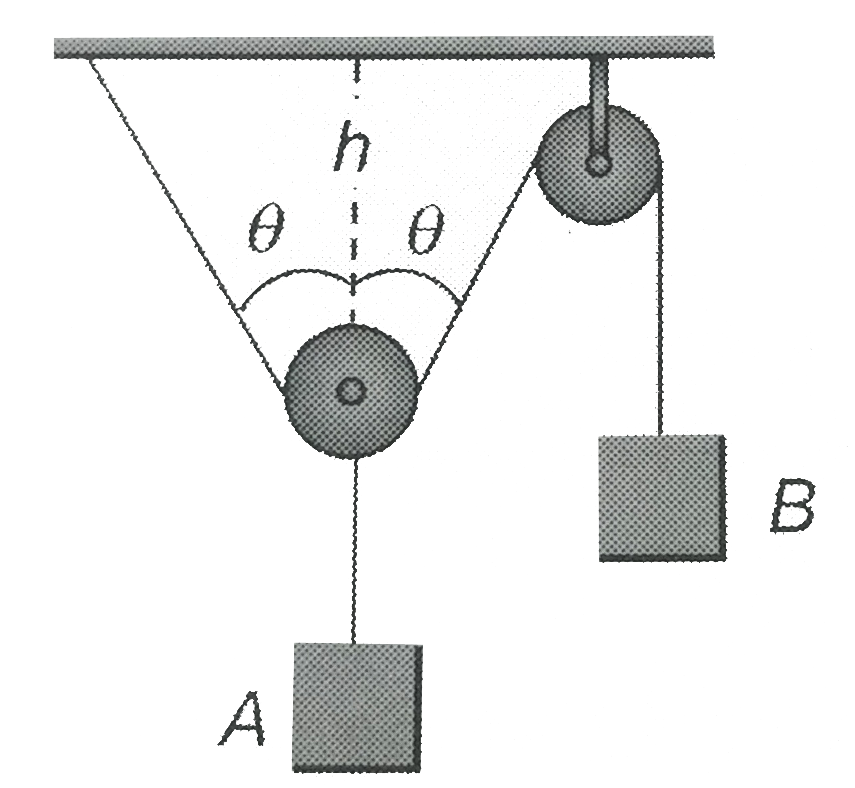
Find the ratio of velcities of block A and B at the instant as shown01:54View Solution
Consider the situation as shown. If a vehicle moves towards right with constant velocity `v_(0)`, find the velocity and acceleration of the block in terms of h and x, where x is the distance traveled by the vehicle towards right.03:03View SolutionA spring of force constant k and natural length 6l is broken in three parts of length ratio 1:2:3 find the spring constant of each part.
01:07View Solution
Find the equivalent spring constant in the following cases:02:16View Solution
A 5-kg block rests on a smooth inclined plane of inclination `37^(@)` as shown in the diagram if the extension of spring is 6cm, find (a) the spring constant (b). If the block is pulled dow the incline 4 cm from its equilibrium position and released, find the initial acceleration of the block.02:38View Solution
Two blocks of masses 5 kg and 10 kg are connected by a massless spring as shown in the diagram. A force of 100 N acts on 10kg mass as shown. At a certain instant the acceleration of 5 kg mass is 12 `m//s^(2)` find the force in the spring and acceleration of 10 kg mass.01:46View Solution
Consider the situation as shown. Initially the spring is unstretched when the block of mass m is released from rest assuming the pulley frictionless and light the spring and string massless. Find the extension of sprinig when the block is in equilibrium also find the maximum extension of the spring.03:43View Solution
EXAMPLES questions and complete solutions for chapter NEWTONS LAWS OF MOTION of CP SINGH PHYSICS (HINGLISH) of Class 11
