Complete Solutions to Exercises of chapter FRICTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FRICTION |
| CP SINGH | Exercises |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
Choose the correct option
03:18View SolutionConsider a car moving on a straight road with a speed of `100m//s`. The distance at which car can be stopped is `[mu_k=0.5]`
02:31View SolutionA car is moving along a stight horizontal road with a speed `v_(0)` . If the coefficient of friction between the tyres and the road is mu, the shortest distance in which the car can be stopped is.
03:10View SolutionTwo cars of unequal masses use similar tyres. If they are moving at the same initial speed, the minimum stopping distance
02:36View SolutionAn ice cube is kept on an inclined plane of angle `30^(@)`. The coefficient to kinetic friction between the block and incline plane is `1//sqrt(3)`. What is the acceleration of the block ?
03:35View SolutionStarting from rest , a body slides down at `45^(@)` inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
09:36View SolutionA smooth block is released at rest on a `45^@` incline and then slides a distance 'd'. The time taken to slide is 'n' times as much to slide on rough incline than on a smooth incline. The coefficient of friction is
05:39View SolutionA block is released from the top of an inclined plane of inclination `theta`. Its velocity at the bottom of plane is `v`. If it slides down a rough inclined plane of the same inclination , its velocity at bottom is `v//2`. The coefficient of friction is
07:31View SolutionThe upper half of an inclined plane of inclination `45^(@)` is perfectly smooth while the lower half is rough. A block starting from rest at the top comes back to rest at the bottom. The coefficient of friction for the lower half is
07:21View SolutionA body is sliding down an inclined plane `(mu = (1)/(2))`. If the normal reaction is twice that of the resultant downward force along the incline , the inclination of plane is
04:00View SolutionA ball is thrown vertically with some velocity . A constant air resistance acts. If the time of ascent is `t_(1)` and that of descent is `t_(2)` , then
08:34View SolutionIn an imaginary atmosphere, the air exerts a small force F on any particle in the direction of the particle's motion. A particle of mass m projected upward takes time `t_1` and reaching the maximum height and `t_2` in the return journey to the original point. Then
06:50View SolutionTwo objects A and B are thrown upward simultaneously with the same speed. The mass of A is greater than the mass of B. Suppose their exerts a constant and equal force of resistance on the two bodies.
05:48View SolutionA ball is thrown vertically upward with speed `10 m//s` and it returns to the ground with speed `8 m//s`. A constant air resistance acts. The minimum height attained by the ball is
06:48View SolutionA particle is projected up a rough inclined plane of inclination `theta` and friction coefficient `mu`. If the time of ascent is half of the time of descent, the friction coefficient `mu` is equal to
09:56View SolutionA particle is projected up a `37^(@)` rough incline with velocity `v_(0)`. If `mu = 1//2`, the speed with which it returns back to the starting point is `v`. Then `v//v_(0)` is
09:31View SolutionAs shown in the figure , the friction force acting on the block is
 02:01View Solution
02:01View SolutionThe friction force acting on the block at time `t = 4 s` will be
 02:22View Solution
02:22View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of `30^@` with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
05:28View SolutionConsider the situation as shown in the figure. Choose the correct option.
 03:58View Solution
03:58View SolutionA block of mass `m` lying on a rough horizontal surface of friction coefficient `mu` is pulled by a force `F` as shown , the limiting friction between the block and surface will be
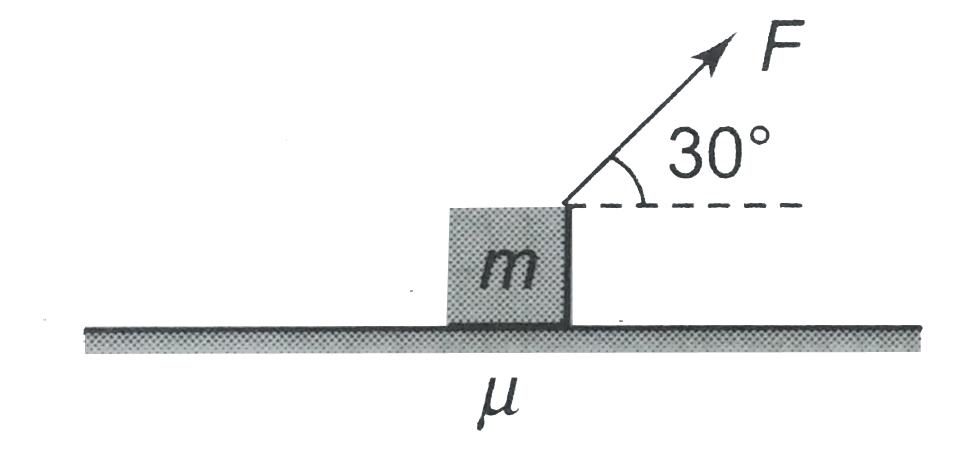 02:34View Solution
02:34View SolutionWhat is the maximum value of the force F such that the block shown in the arrangement, does not move?
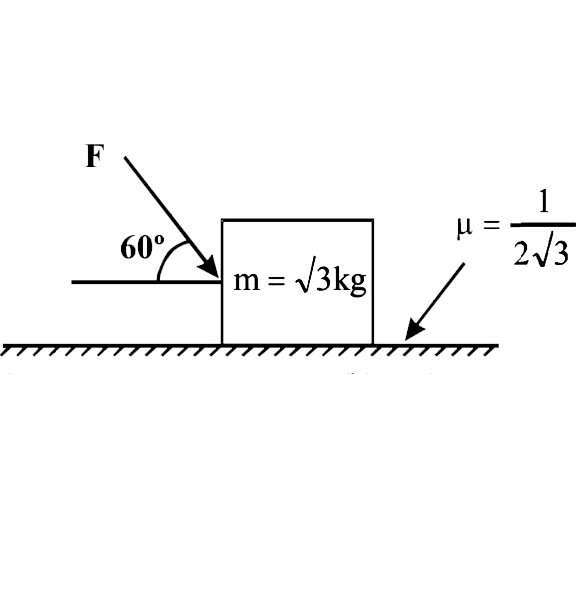 05:42View Solution
05:42View SolutionPulling force making an angle `theta` to the horizontal is applied on a block of weight `W` placed on a horizontal table. If the angle of friction is `alpha`, then the magnitude of force is `alpha` , then the magnitude of force required to move the body is equal to
06:25View SolutionThe acceleration of the block is
 03:30View Solution
03:30View SolutionA lift is moving downwards with an acceleration equal to `g`. A block of mass `m` , kept on the floor of the lift of friction coefficient `mu` , is pulled horizontally . The friction acting on the block is
02:10View SolutionA block of mas `m` begins to slide down on an inclined plane of inclination `theta`. The force of friction will be
02:50View SolutionA body of mass `10 kg` is lying on a rough inclined plane of inclination `37^(@)` and `mu = 1//2` , the minimum force required to pull the body up the plane is
03:57View SolutionA block is at rest on an inclined plane making an angle `alpha` with the horizontal . As the angle `alpha` of the incline is increased the block starts slipping when the angle of inclination becomes `theta`. The coefficient of static friction between the block and the surface of the inclined plane is or A body starts sliding down at an angle `theta` to the horizontal. Then the coefficient of friction is equal to
03:34View SolutionA block of `3 kg` rests in limiting equilibrium on an inclined plane of inclination `30^(@)`. If the plane is raised to an inclination `60^(@)` , the force along the plane required to support it is
04:22View SolutionA block rests on a rough inclined plane making an angle of `30^(@)` with horizontal. The coefficient of static friction between the block and inclined plane is `0.8` . If the frictional force on the block is `10 N`, the mass of the block in `kg` is `(g = 10 m//s^(2))`
01:54View SolutionThe force required just to move a body up an inclined plane is double the force required just to prevent the body sliding down. If the coefficient of friction is `0.25` , the angle of inclination of the plane is
08:02View SolutionA `10 kg` block is initially at rest on a rough horizontal surface. A horizontal force of `60 N` is required to set the block in motion . After it is in motion , a horizontal force of `50 N` is required to keep the block moving with constant velocity . The ratio coefficient of static and kinetic friction is
03:25View SolutionTwo blocks `A` and `B` , each of mass `10 kg` , are connected by a light string passing over a smooth pulley as shown in the figure. Block `A` will remain at rest if the friction on it is
 04:16View Solution
04:16View SolutionA uniform rope of `length L meters` is lying over a table. If the coefficient of friction be `mu`, then the maximum length `L_(1)` of the part of the rope which can overhang the edge without sliding is
06:07View SolutionA uniform metal chain is placed on a rough table such that the one end of chain hangs down over the edge of the table, when one-third of its length hang over the edge, the chain starts sliding. Then the coefficient of static friction is
03:33View SolutionConsider the situation as shown in the figure.
The maximum value of `m` so that the blocks do not move is
 02:40View Solution
02:40View SolutionTwo masses `A` and `B` of `10 kg` and `5 kg`, respectively , are connected with a string passing over a frictionless pulley fixed at the corner of a table as shown. The coefficient of static friction between `A` and the table is `0.2`. The minimum mass `C` that should be placed on `A` to prevent it from moving is equal to
 03:53View Solution
03:53View SolutionTwo block of masses `M_(1)` and, `M_(2)` are connected with a string which passed over a smooth pulley . The mass `M_(1)` is placed on a tough inclined plane as shown in figure .The coefficient of friction between and block and the inclined plane is `mu` what should be the minimum mass `M_(2)` so that the block `M_(1)` slides upwards?
 02:35View Solution
02:35View SolutionA car accelerates on a horizontal road due to the force exerted by
01:37View SolutionWhich of the following is correct , when a person walks on the rough surface.
02:18View SolutionWhile walking on ice, one should take small steps to avoid sliping. This is because smaller steps ensure
05:07View SolutionA box is placed on an inclined plane and has to be pushed down.The angle of inclination is
02:17View SolutionA boy of mass M is applying a horizontal force to slide a box of mass M on a rough horizontal surface. The floor is `mu` and the between the box and the floor is `mu'`. In which of the following cases it is certainly not possible to slide the box?
05:57View SolutionA conveyor belt is moving at a constant speed of `2m//s` . A box is gently dropped on it. The coefficient of friction between them is `mu=0.5` . The distance that the box will move relative to belt before coming to rest on it taking `g=10ms^(-2)` is:
04:48View SolutionA car starts from rest on a `1600 m` long bridge. The coefficient of friction between the tyre and road is `0.8`. The minimum time taken by the car to cross the bridge is
02:55View SolutionMark the correct statements about the friction between two bodies
03:20View SolutionConsider a vehicle going on a horizontal rod towards east. Neglect any force by the air. The frictional forces on the vehicle by the road
02:53View SolutionA block is placed on a rough floor and a horizontal force F is applied on it.The force of friction f by the floor on the block is measured for different values of F and a graph is plotted between them.
03:48View SolutionA body of mass M is kept n a rough horizontal surfasce (friction coefficient `=mu`). A person is trying to pull he body by applying a horizontal force but the body is not moving. The force by the surface on A is F, where
04:12View SolutionThe contact force exerted by a body A on another body B is equal to the normal force between the bodies. We concude that
02:39View SolutionLet `F,F_N and f` denote the magnitudes of the contact force, normal force and the friction exerted by one surface on the other kept in contact. If none of these is zero,
03:59View SolutionA small block of mass of `0.1 kg` lies on a fixed inclined plane `PQ` which makes an angle `theta` with the horizontal. A horizontal force of `1N` acts on the block through its centre of mass as shown in the figure. The block remains stationary if ( take `g=10 m//s^(2))`
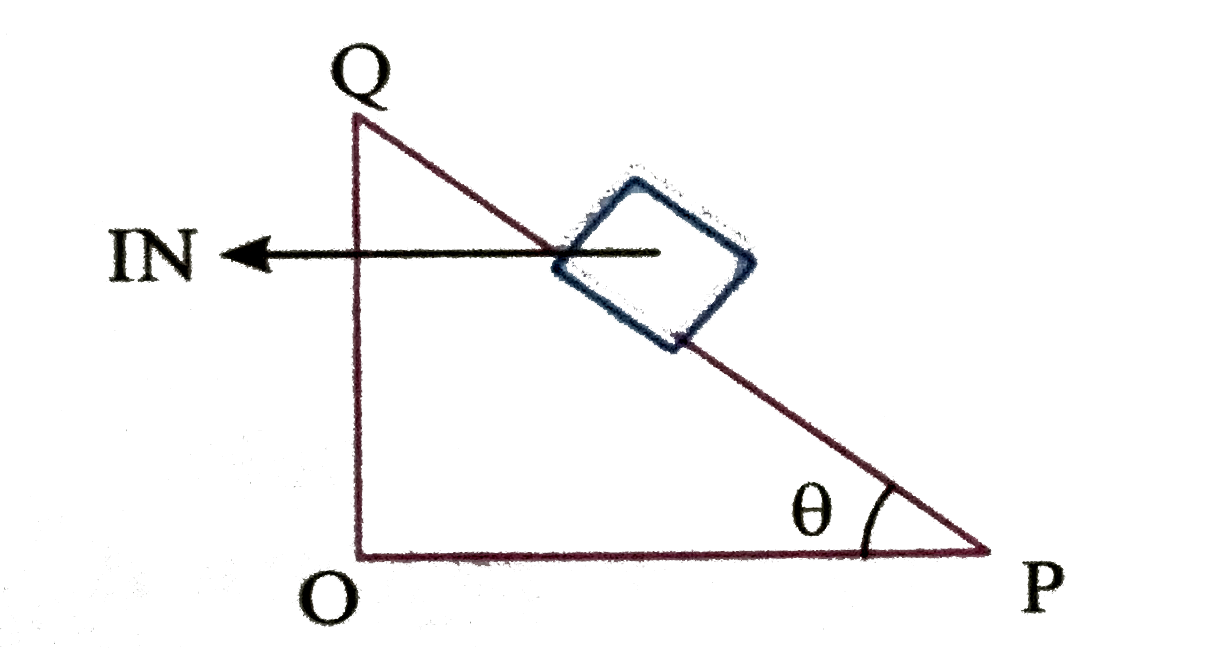 02:14View Solution
02:14View SolutionA circular disc with a groove along its diameter is placed horizontally on a rough surface. A block of mass 1 kg is placed as shown. The co-efficient of friction between the block and all surfaces of groove and horizontal surface in contact is `mu=2/5`. The disc has an acceleration of `25m//s^2` towards left. Find the acceleration of the block with respect to disc. Given `cos theta=4/5`, `sin theta=3/5`.
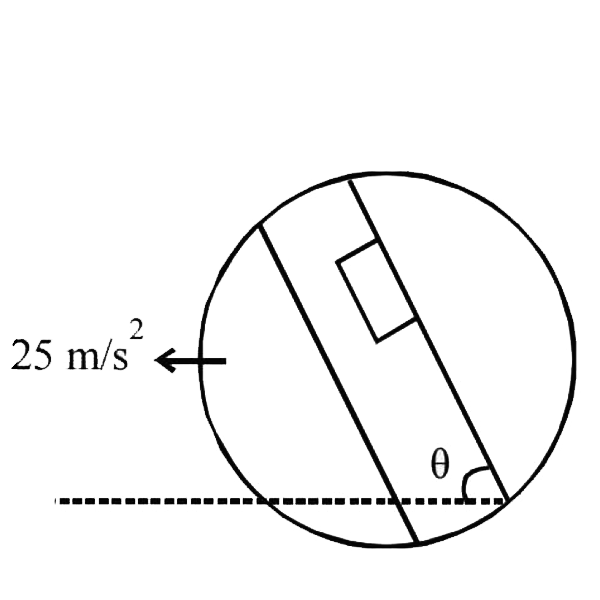 04:50View Solution
04:50View SolutionThe minimum acceleration that must be impprted to the cart in the figure so that the block `A` will not fall (given `mu` is the coefficient if friction between the surface of block and cart) is given by:
 03:01View Solution
03:01View SolutionConsider the situation as shown in the diagram.
The coefficient of friction between the block is `0.5`. The acceleration of the lower block is02:44View SolutionIn the previous problem , if the applied force is made `20 N` , the acceleration of the upper and the lower blocks will be
03:57View SolutionA 40kg slab rests on a frictionless floor as shown in the figure. A 10kg block rests on the top of the slab. The static coefficient of friction between the block and slab is `0.60` while the kinetic friction is `0.40` . The 10kg block is acted upon by a horizontal force 100N. if `g=9.8m//s^(2)` , the resulting acceleration of the slab will be.
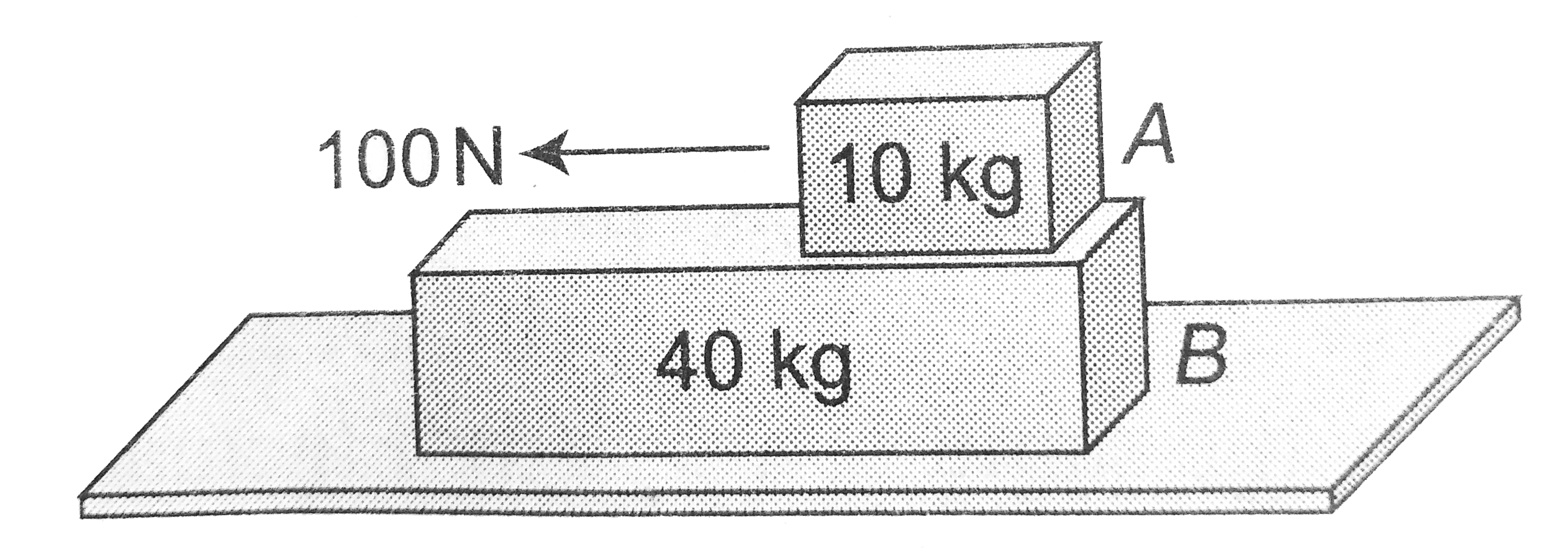 06:50View Solution
06:50View SolutionA block `B` is placed on the block `A`.The mass of block `B` is less than the mass of block `A`. Friction exists between the blocks , whereas the ground on which block `A` is placed is taken to be smooth. A horizontal force `F`, increasing linearly with time begins to act on `B`. The acceleration `a_(A)` and `a_(B)` of blocks `A` and `B`, respectively , are plotted against `t`. The correctly plotted graph is
 06:34View Solution
06:34View SolutionTwo blocks of mass `m_(1) = 6 kg` and `m_(2) = 3kg` are as shown in the diagram. Coefficient of friction between `m_(1)` and `m_(2)` and between `m_(1)` and `m_(2)` and between `m_(1)` and the surface is `0.5` and `0.4` , respectively . The maximum horizontal force that can be applied to the mass `m_(1)` so that they move without separation is
 07:07View Solution
07:07View SolutionThe rear side of a truck is open and a box of mass `2 kg` is placed on the truck `8 meters` away from the open end. `mu = 0.1` and `g = 10 m//s^(2)`. The truck starts from rest with an acceleration of `2 m//s^(2)` on a straight road. The box will fall off the truck when it is at distance from the starting point equal to
06:11View SolutionThe friction acting on the upper block is
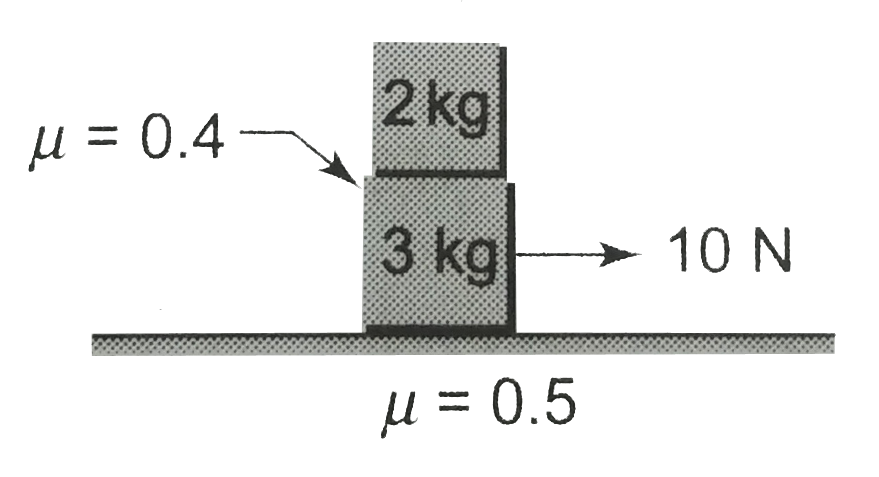 02:40View Solution
02:40View SolutionA block `A` of mass `200 kg` rest on a block `B` of mass `300 kg`. `A` is tied with a horizontal string to a wall. Coefficient of friction between `A` and `B is 0.25` and that between `B` and floor is `0.2`. The horizontal force `F` needed to move the block `B` is
 04:23View Solution
04:23View SolutionA system consists of three masses `m_(1)` , `m_(1)` , `m_(1)` , `m_(2)` and `m_(3)` connected by a string passing over a pulley `P` . The mass `m_(1)` hangs freely and `m_(2)` and `m_(3)` are on a rough horizontal table (the coefficient of friction=mu) The pulley is frictionless and of negligible mass. The downward acceleration of m`1` is (Assume `m_(1)=m_(2)=m_(3)=m`).
 05:44View Solution
05:44View Solution
Exercises questions and complete solutions for chapter FRICTION of CP SINGH PHYSICS (HINGLISH) of Class 11
