Complete Solutions to EXERCISE of chapter GRAVITATION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | GRAVITATION |
| CP SINGH | EXERCISE |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
Two identical copper spheres of radius `R` are in contact with each other. If the gravitational attraction between them is `F`, find the relation between `F` and `R`.
02:20View SolutionTwo sphere of masses `m` and `M` are situated in air and the gravitational force between them is `F`. The space around the masses in now filled with a liquid of specific gravity `3`. The gravitational force will now be
01:26View SolutionTwo particles of equal mass `'m'` go around a circle of radius `R` under the action of their mutual gravitaitonal attraction. The speed of each particle with respect to their centre of a mass is -
03:13View SolutionTwo point masses A and B having masses in the ratio `4:3` are separated by a distance of 1m. When another point mass C of mass M is placed in between A and B, the force between A and C is `(1/3)^(rd)` of the force between B and C. Then the distance C from A is
04:57View SolutionIf `R` is the radius of the earth and `g` the acceleration due to gravity on the earth's surface, the mean density of the earth is
01:06View SolutionMass remaining constant, the radius of the earth shrinks by 1%. The acceleration due to gravity on the earth's surface would
03:21View SolutionTwo planets have the same average density but their radii are `R_(1)` and `R_(2)`. If acceleration due to gravity on these planets be `g_(1)` and `g_(2)` respectively, then
02:06View SolutionThe density of a newly discovered planet is twice that of earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the earth. If the radius of the earth is `R`, the radius of the planet would be
03:20View SolutionAcceleration due to gravity on moon is `1//6` of the acceleration due to gravity on earth. If the ratio of densities of earth `(rho_(e))` and moon `(rho_(m))` is `((rho_(e))/(rho_(m)))=5/3` then radius of moon `(R_(m))` in terms of `R_(e)` will be
04:34View SolutionConsider a planet in some solar system which has a mass double the mass of the earth and density equal to the average density of the earth. An object weighing W on the earth will weigh
05:01View SolutionWhich graph correctley presents the variation of acceleration due to gravity with the distance form the centre of the earth?
02:20View SolutionLet the acceleration due to gravity be `g_(1)` at a height `h` above the earth's surface `g_(2)` at a depth `d` below the earth's surface. If `g_(1)=g_(2),h lt lt R` and `d lt lt R` then
02:58View SolutionThe weight of an object in the coal mine, sea level and at the top of the mountain are `W_(1),W_(2)` and `W_(3)` respectively, then
03:37View SolutionSuppose the earth increases its speed of rotation . At what new time period will the weight of a body on the equator becomes zero? Take `g=10 m/s^2` and radius of the earth `R=6400 km`.
01:50View SolutionSuppose the acceleration due to gravity at earth's surface is `10ms^-2` and at the surface of Mars it is `4.0ms^-2`. A passenger goes from the to the mars in a spaceship with a constant velocity. Neglect all other object in sky. Which part of figure best represent the weight (net gravitational force) of the passenger as a function of time?
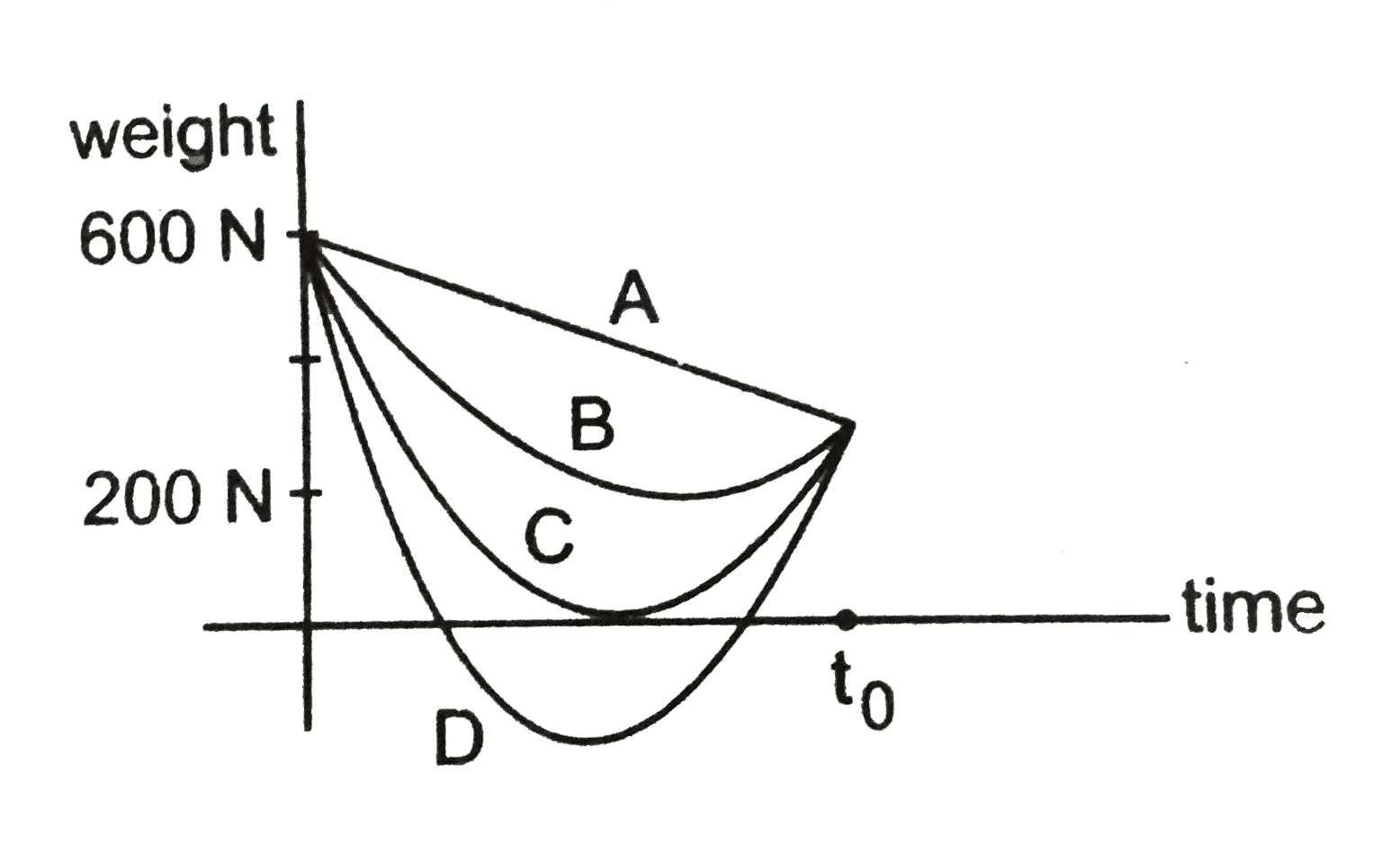 02:38View Solution
02:38View SolutionTwo bodies of masses m and 4m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero is:
04:30View SolutionFour particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
04:00View SolutionInfinite number of masses, each of `1 kg`, are placed along the x-axis at `x = +- 1m, +- 2m, +-4m, +- 8m, +- 16m`.. The gravitational of the resultant gravitational potential in term of gravitaitonal constant `G` at the origin `(x = 0)` is
04:27View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance `a/2` from the centre.
05:01View SolutionThe magnitude of the gravitational field at distance `r_(1)` and `r_(2)` from the centre of a uniform sphere of radius `R` and mass `M` are `F_(1)` and `F_(2)` respectively. Then:
03:35View SolutionA spherically symmetric gravitational system of particles has a mass density` rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):}` where`rho_0` is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce `r(0ltrltOO)` form the centre of the system is represented by
03:38View SolutionA planet is moving in an elliptic orbit. If `T,V,E` and `L` stand, respectively, for its kinetic energy, gravitational potential energy, total energy and angular momentum about the centre of force, then
05:24View SolutionA satellite revolves around the earth in an elliptical orbit. Its speed is
03:50View SolutionFor a planet moving and the sun in an elliptical orbit, which of the following quantities remain constant?
(i) The total energy of the 'sun plus planet' system
(ii) The angular momentum of the planet about the sun
(iii) The force of attraction between the two
(iv) The linear momentum of the planet04:10View SolutionWhich of the following quantities remain constant in a planetary motion (consider elliptical orbits)as seen from the sun?
01:55View SolutionFigure shows the motion of a planet around the Sun `S` in an elliptical orbit with the Sun at the focus. The shaded areas `A` and `B` are also shown in the figure which can be assumed to be equal. If `t_(1)` and `t_(2)` represent the time taken for the planet to move from `a` to `b` and `c` to `d`, respectively then
 01:19View Solution
01:19View SolutionThe earth `E` moves in an elliptical orbit with the sun `S` at one of the foci as shown in figure. Its speed of motion will be maximum at the point
 01:52View Solution
01:52View SolutionThe largest and the shortest distance of the earth from the sun are `r_(1)` and `r_(2)`, its distance from the sun when it is at the perpendicular to the major axis of the orbit drawn from the sun
06:04View SolutionA plenet moving along an elliptical orbit is closest to the sun at a distance `r_(1)` and farthest away at a distance of `r_(2)`. If `v_(1)` and `v_(2)` are the linear velocities at these points respectively, then the ratio `(v_(1))/(v_(2))` is
02:05View SolutionIf the distance between the earth and the sun were half its present value, the number of days in a year would have been
02:20View SolutionThe mean radius of the earth's orbit of mercury is `6xx10^(10)m`. The mercury will revolve around the sun in nearly
02:14View SolutionThe radius of the earth`R` and acceleration due to gravity at its surface is `g`. If a body of mass `m` is sent to a height of `R//4` from the earth's surface, the potential energy increases by
03:55View SolutionIn the previous problem, the minimum speed with which the body must be thrown from the surface of the earth so as to reach a height of `R//4` is
04:37View SolutionIf the acceleration due to gravity at the surface of the earth is g, the work done in slowly lifting a body of mass m from the earth's surface to a height R equal to the radius of the earth is
01:56View SolutionA small mass `m` is moved slowly from the surface of the earth to a height `h` above the surface. The work done (by an external agent) in doing this is
03:39View SolutionA particle is projected vertically upwards with a velocity `sqrt(gR)`, where `R` denotes the radius of the earth and `g` the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
04:52View SolutionA projectile is projectile with velocity `kv_(e)` in vertically upward direction from the ground into the space (`v_(e)` is escape velocity and `klt1`). If air resistance is considered to be negligible then the maximum height from the centre of earth to which it can go, will be : (`R`=raduis of earth)
04:33View SolutionAn asteroid of mass `m` is approaching earth, initially at a distance `10R_(E)` with speed `v_(i)`. It hits earth with a speed `v_(f)` (`R_(E)` and `M_(E)` are radius and mass of earth),. Then
03:20View SolutionThe gravitational force between two objects is proportional to `1//R` (and not as `1//R^(2)`) where `R` is separation between them, then a particle in circular orbit under such a force would have its orbital speed `v` proportional to
01:38View SolutionSuppose the gravitational force varies inversely as the nth power of distance. Then the time period of a planet in circular orbit of radius 'R' around the sun will be proportional to
02:37View SolutionThe distance of two satellites from the surface of the earth `R` and `7R`. There time periods of rotation are in the ratio
02:16View SolutionA satellite is launched into a circular orbit of radius `R` around the earth. While a second is lunched into an orbit of radius `1.01R` The period of the second satellite is longer than the first one by approximately:
03:08View SolutionTwo small satellies move in a circular orbits around the earth, at disatnce `r` and `(r + dr)` from the centre of the earth. Their time periods of rotation ate `T` and `T + dT (Delta r lt lt r, DeltaT lt lt T)`. Then
02:43View SolutionThe period of a satellite moving in a circular orbit near the surface of a planet is independent of
02:11View SolutionThe mean radius of the earth is `R`, its angular speed on its own axis is `omega` and the acceleration due to gravity at earth's surface is `g`. The cube of the radius of the orbit of a geo-stationary satellite will be
03:19View SolutionTwo satellites of earth `S_(1)` and `S_(2)` are moving in the same orbit. The mass of `S_(1)` is four times the mass of `S_(2)`. Which one of the following statements is true?
03:49View SolutionIf a satellite orbits as close to the earth's surface as possible,
04:13View SolutionIn a satellite if the time of revolution is `T`, then kinetic energy is proportional to
01:54View SolutionTo an astronaut is a spcaceship, the sky appears
01:26View SolutionA person sitting in a chair in a satellite feels weightless because
02:17View SolutionAn astronaut orbiting the earth in a circular orbit `120km` above the surface of earth, gently drops a spoon out of space-ship. The spoon will
02:36View SolutionA geostationary satellite should be launched such that it moves from
01:43View Solutionfor a satellite to be geostationary, which of the following are essential conditions?
(i) It must always be stationed above the equator.
(ii) It must rotates from west to east.
(iii) It must be about `36,000 km` above the earth
(iv) Its orbit must be circular and not elliptical.View SolutionFor a satellite to orbit around the earth, which of the following must be true?
02:50View SolutionThe additional kinetic energy to be provided to a satellite of mass `m` revolving around a planet of mass `M`, to transfer it forms a circular orbit of radius `R_(1)` to another of radius `R_(2)(R_(2)gtR_(1))` is
02:51View SolutionA satellite close to the earth is in orbit above the equator with a period of rotation of `1.5` hours. If it is above a point `P` on the equtor at some time, it will be above `P` again after time ...........
04:00View SolutionA satellite orbits around the earth in a circular orbit with a speed `upsilon` and orbital radius `r`. If it loses some energy, then `upsilon` and `r` changes as
02:15View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
03:07View SolutionThe escape Velocity from the earth is `11.2 Km//s`. The escape Velocity from a planet having twice the radius and the same mean density as the earth, is :
02:31View SolutionThe kinetic energy needed to project a body of mass m from the eath surface (radus R) to infinity is
01:35View SolutionA body is orbiting very close to the earth surface kinetic energy K.E. The energy required to completely escape from it is
04:21View SolutionThe escape velocity of a body from earth's surface is `v_e`. The escape velocity of the same body from a height equal to `7R` from earth's surface will be
02:33View SolutionThe escape velocity for a body projected vertically upwards from the surface of earth is 11km/s. If the body is projected at an angle of `45^@` with the vertical, the escape velocity will be
01:03View SolutionThe mass of a spaceship is 1000kg. It is to be launched from the earth's surface out into free space. The value of g and R (radius of earth) are `10m/s^2` and 6400 km respectively. The required energy for this work will be:
01:26View SolutionThere are two planets. The ratio of radius of two planets is `k` but ratio of acceleration due to gravity of both planets is g. What will be the ratio of their escape velocity ?
01:43View SolutionThere is no atomosphere on moon because
01:50View SolutionA projectile is launched from the surface of earth with a velocity less than the escape velocity. Its total mechanical energy is
03:33View SolutionThe ratio of the K.E. required to the given to the satellite to escape earth's gravitational field to the K.E. required to be given so that the satellite moves in a circular orbit just above earth atmosphere is
02:36View SolutionThe escape velocity for a planet is `v_e`. A particle is projected from its surface with a speed `v`. For this particle to move as a satellite around the planet.
02:16View SolutionA particle of mass 'm' is projected from the surface of earth with velocity `upsilon =2upsilon_(e)`, where `upsilon_(e)` is the value of escape velocity from the surface of earth . Find velocity of the particle on reaching to interstellar space (at infinity) in terms of `upsilon_(e)`.
05:02View SolutionThe earth is assumed to be a sphere of raduis `R`. A plateform is arranged at a height `R` from the surface of the `fv_(e)`, where `v_(e)` is its escape velocity form the surface of the earth. The value of `f` is
04:12View SolutionA satellite is moving with a constant speed 'V' in a circular orbit about the earth. An object of mass 'm' is ejected from the satellite such that it just escapes form the gravitational pull of the earth. At the tme of its ejection, the kinetic energy of the object is
03:25View SolutionAn object is weighted at the North Pole by a beam balance and a spring balance, giving readings of `W_B` and `W_S` respectively. It is again weighed in the same manner at the equator, giving readings of `W'_B` and `W'_S` respectively. Assume that the acceleration due to gravity is the same everywhere and that the balance are quite sensitive, Choose the wrong option
05:52View SolutionLet `omega` be the angular velocity of the earth's rotation about its axis. Assume that the acceleration due to gravity on the earth's surface has the same value at the equator and the poles. An object weighed by a spring balance gives the same reading at the equator as at a height `h` above the poles `(h lt lt R)`. The value of `h` is
03:55View SolutionLet `omega` be the angular velocity of the earth's rotation about its axis. Assume that the acceleration due to gravity on the earth's surface has the same value at the equator and the poles. An object weighed at the equator gives the same reading as a reading taken at a depth `d` below earth's surface at a pole `(dlt ltR)`. the value of `d` is-
02:42View SolutionTwo bodies of masses `m_1` and `m_2` are initially at rest at infinite distance apart. They are then allowed to move towards each other under mutual gravitational attraction. Their relative velocity of approach at a separation distance `r` between them is.
04:36View SolutionA double star is a system of two stars of masses `m` and `2m`, rotating about their centre of mass only under their mutual gravitational attraction. If `r` is the separation between these two stars then their time period of rotation about their centre of mass will be proportional to
04:28View SolutionThree point masses are at the corners of an equilateral traingle of side `r`. Their separations do not change when the system rotates about the centre of the triangle. For this, the time period of rotation must be proportional to
04:14View SolutionA point `P` lies on the axis of a fixed ring of mass `M` and radius `a`, at a distance `a` from its centre `C`. A small particle starts from `P` and reaches `C` under gravitational attraction only. Its speed at `C` will be.
04:00View SolutionThe escape velocity for a planet is `v_e`. A particle starts from rest at a large distance from the planet, reaches the planet only under gravitational attraction, and passes through a smooth tunnel through its centre. Its speed at the centre of the planet will be
03:40View SolutionA small body of superdense material, whose mass is twice the mass of the earth but whose size is very small compared to the size of the earth, starts form rest at a height `H lt lt R` above the earth's surface, and reaches the earth's surface in time `t`. then `t` is equal to
04:37View SolutionIn the previous questions, if the mass of the body is half the mass of the earth, and all other data remain the same, then `t` is equal to
03:55View SolutionA binary star system consists of two stars A and B which have time period `T_A and T_B, radius R_Ba` and mass `M_a and M_B.` Then
02:26View SolutionThe escape velocity for a planet is `v_(e)`. A tunnel is dug along a diameter of the planet and a small body is dropped into it at the surface. When the body reaches the centre of the planet, its speed will be
05:50View SolutionA train A runs from east to west and another train B of the same maas runs from west to east at the same speed along the equator. A presses the track with a force `F_1 and B` presses the track with a force F.
07:30View SolutionThe condition for a uniform spherical mass `m` of a radius `r` to be a black hole is [`G` =gravitational constant and `g`=acceleration due to gravity]
01:42View Solution
EXERCISE questions and complete solutions for chapter GRAVITATION of CP SINGH PHYSICS (HINGLISH) of Class 11
