In the following situations, the length and area of cross-section of each rod is same. Find temperature θ at junction of rods.
(a) 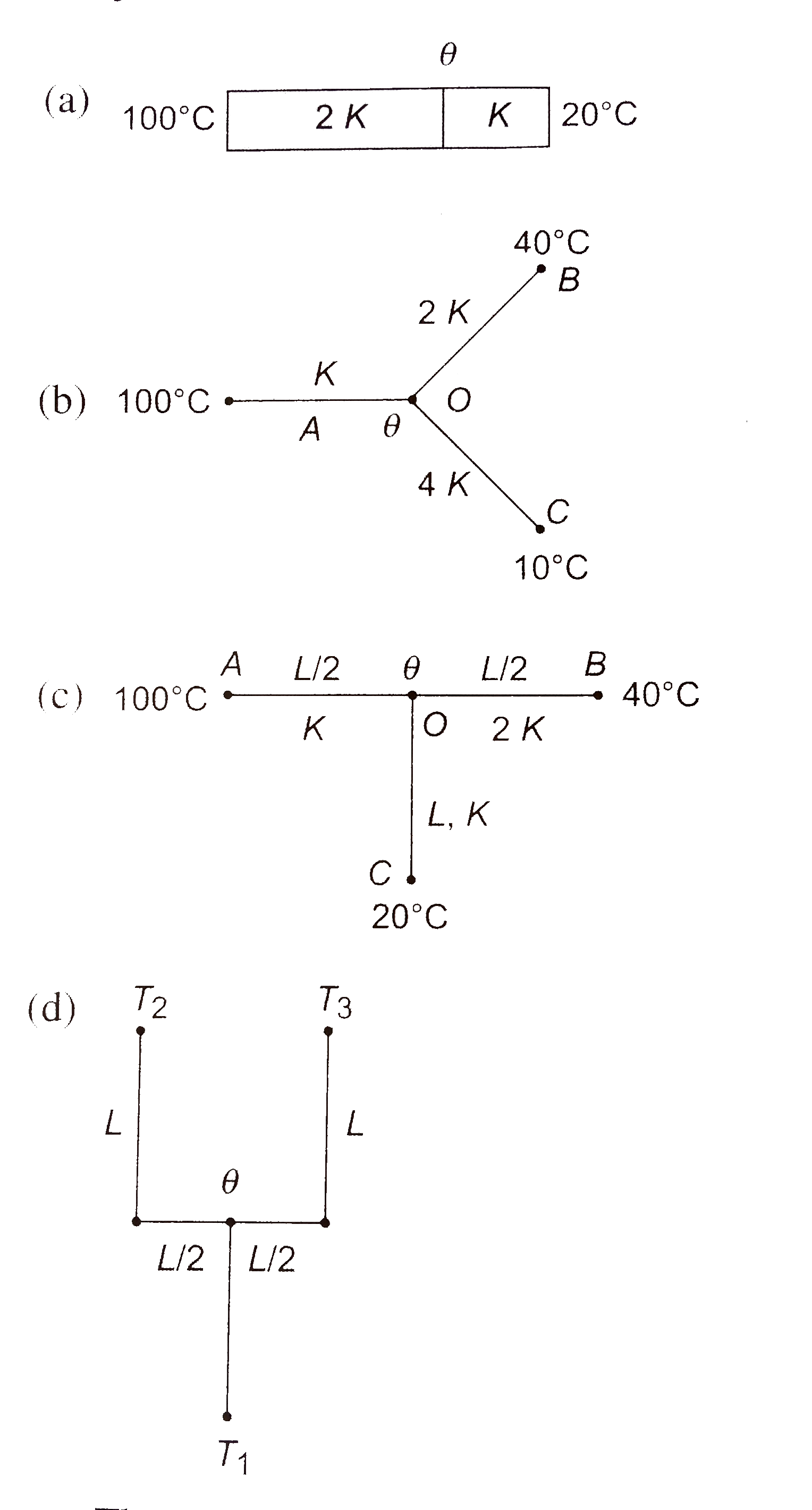
(b) 
(c ) 
(d) 
The thermal conductivity of each rod is K.
(a) Thermal resistance of rod 1
R1=L2Ka=R0
Thermal resistance of rod 2
R2=LKA=2R0
Heat current in rods is same
i=ΔθR
i=100−θR1=θ−20R2
100−θR0=θ−202R0
200−2θ=θ−20
3θ=220
θ=2203.∘C
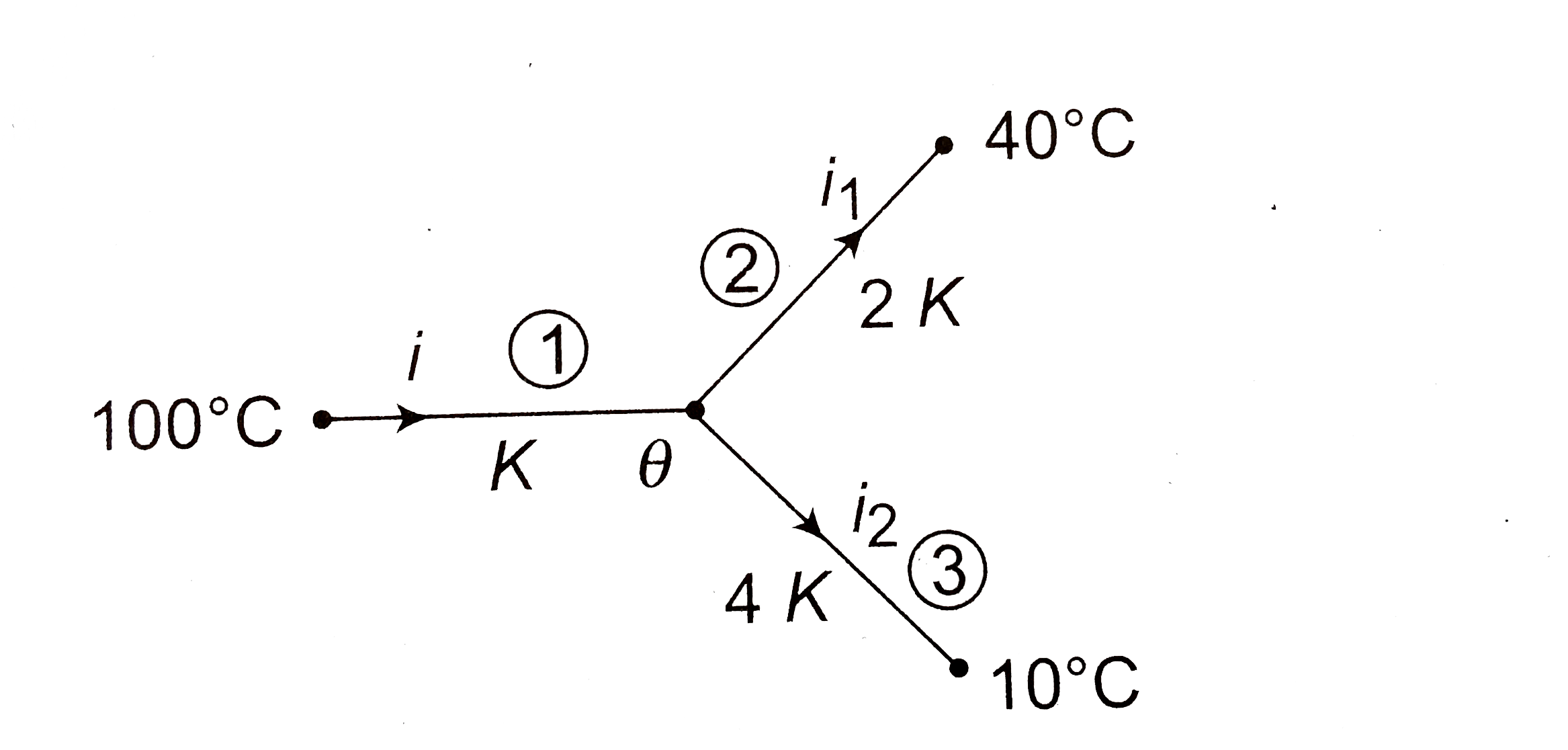
(b) R1LKA=R0
R2=L2KLa=R02
R3=L4KA=R04
i=i1+i2
100−θR1=θ−40R2+θ−10R3
100−θR0=θ−40R0/2+θ−10R0/4
100−θ=0(θ−40)+4(θ−10)
=2θ−80+40−40
7θ=220
θ=2207.∘C
(c ) R1=L/2KA=L2KA=R0
R2=LKA=2R0
R3=L/22KA=L4KA=R02
i=i1+i2
100−θR1=θ−20R2+θ−40R3
100−θR0=θ−202R0+θ−40R0/2
100−θ=θ−202+2(θ−40)
200−2θ=θ−20+4θ−160
7θ=380
θ=3807.∘C
Let LKA=R
i=i1+i2
T1−θR=θ−T2R+R2+θ−T3R+R2
T1−θ=23(2θ−T2−T3)
3T1−3θ=4θ−2T2−2T3
7θ=3T1+2T2+2T3
θ=3T1+2T2+2T37

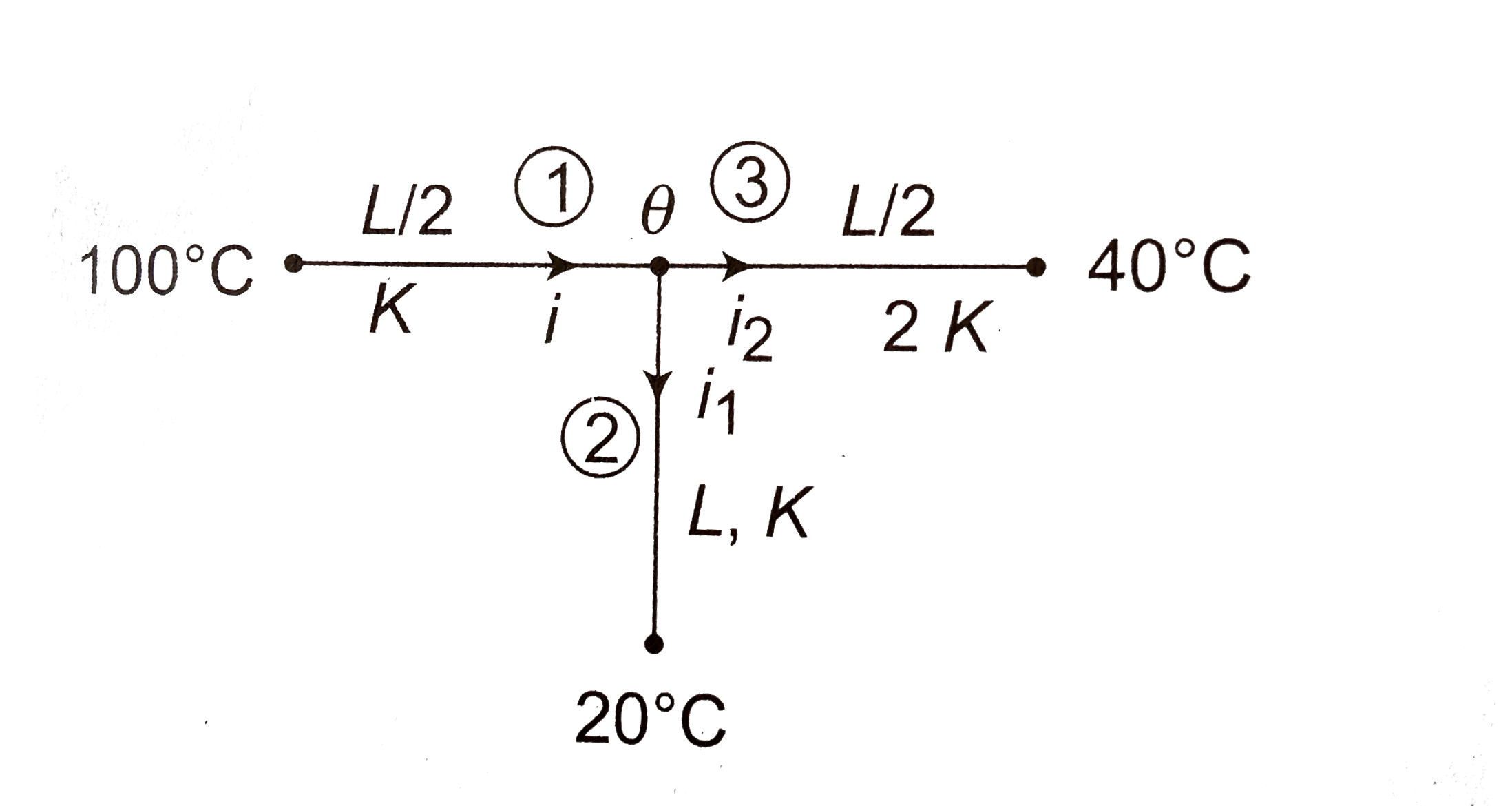

Topper's Solved these Questions
Similar Questions
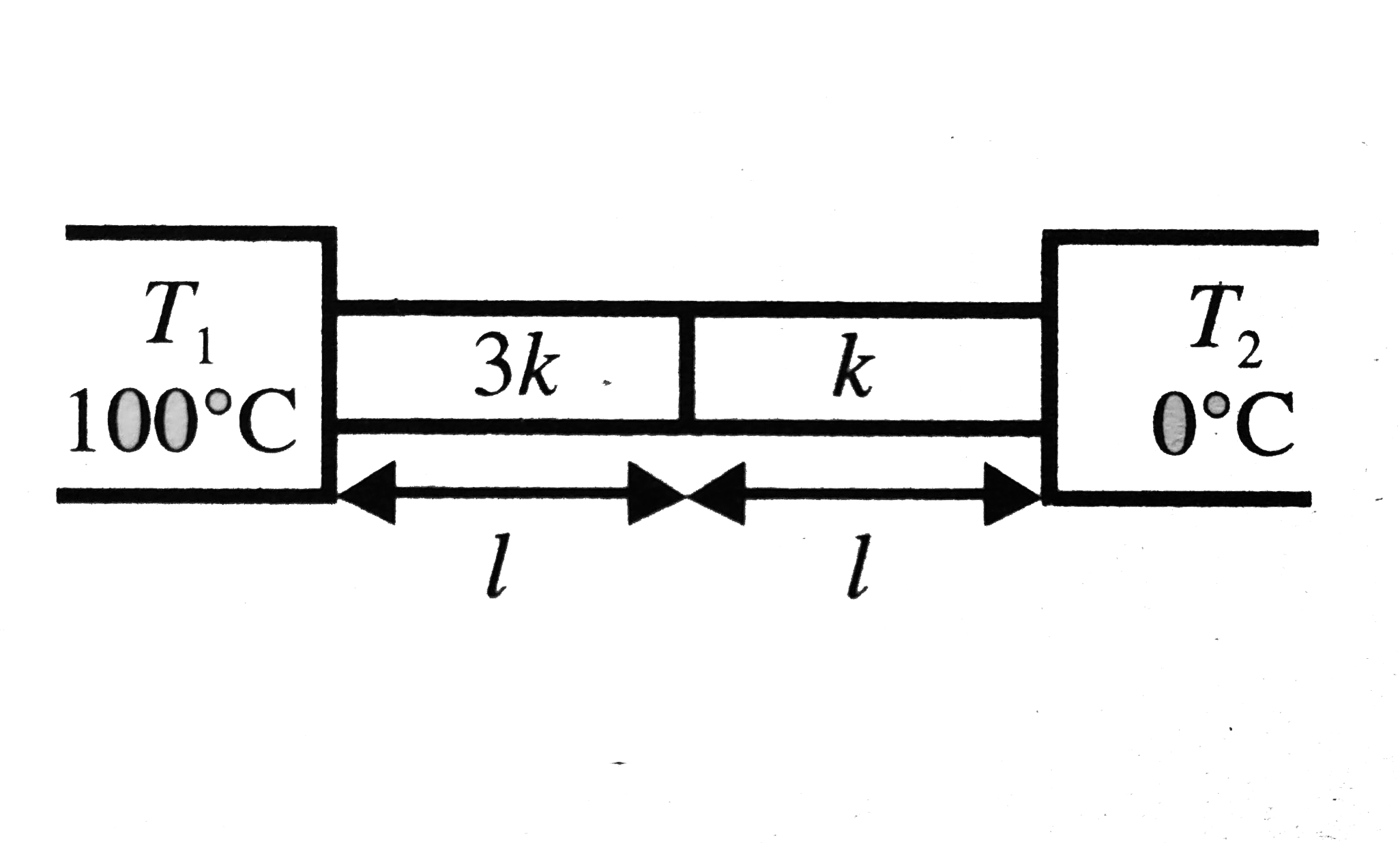
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View Solution
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View Solution
Knowledge Check
Three rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
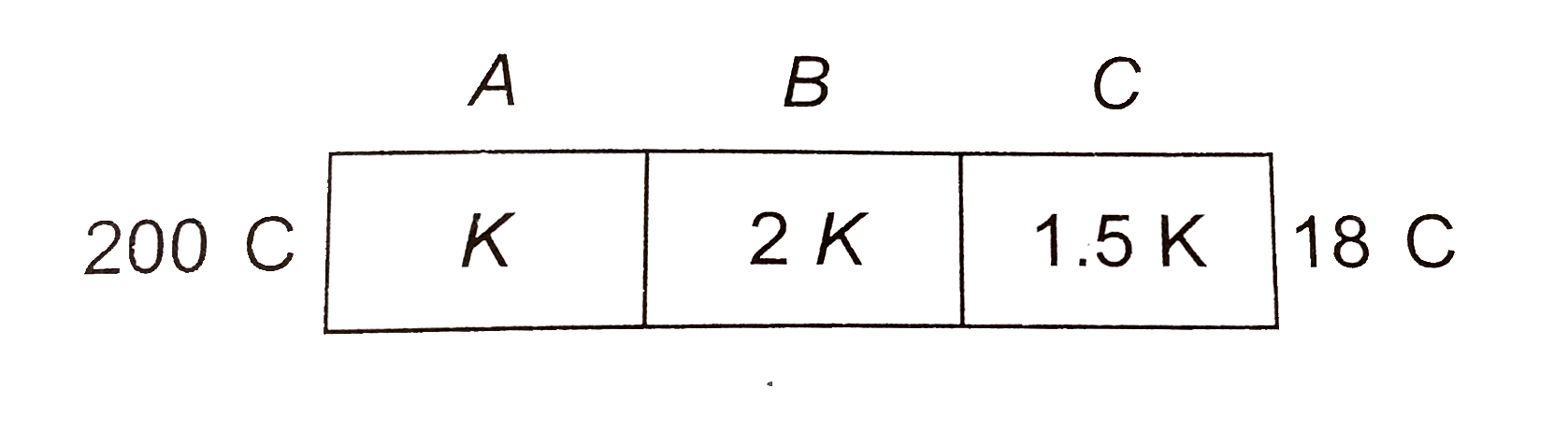 A74∘CB116∘CC156∘CD148∘C
A74∘CB116∘CC156∘CD148∘CTwo rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
AA1A2=L1K2BA1A2=K2K1CA1A2=K1K2Dplaced in hot oilThree metal rod A, B and C of same length and cross-section are placed end to end and a temperature difference is maintained between the free ends of A and C. If the thermal conductivity of B(KB) is twice that of C(KC) and half that of A(KA), then the effective thermal conductivity of the system will be
AKA7B6KB7C7KB3D7KC
Find the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1) . Thermal conductivity of the material of the rod is K.

View SolutionFind the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1 . Thermal conductivity of the material of the rod is K.

View SolutionTwo rods of same length and area of cross-section A1 andA2 have their ends at the same temperature. If K1andK2 are their thermal conductivities, c1andc2 are their specific heats and d1and d2 are their densities, then the rate of flow of heat is the same in both the rods if
View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
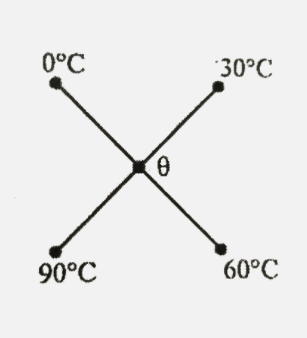
View SolutionFour rods of material X and three rods of material Y are connected as shown in figure. All the rods are of identical lengths and cross-sectional area. Given thermal resistance of rod of material X,Rx=R and thermal conductivities of materials are related by relation KY=2KX.
_E01_157_Q01.png)
Column-IColumn-II(A)Thermal resistance between B and E(p)50013.∘C(B)Thermal resistance between A and F(q)70013.∘C(C)Temperature of junction B(r)2R3(D)Temperature of junction D(s)13R6
View Solution
